@import url(http://www.shnenglu.com/CuteSoft_Client/CuteEditor/Load.ashx?type=style&file=SyntaxHighlighter.css);@import url(/css/cuteeditor.css);
| 《實時計算機圖形學(xué)(第二版)》 |
3.5.2 透視投影 |
P36 |
| 《Real-time Rendering,Second Edition》 |
3.5.2 Perspective Projection |
P61 |
如何證明q
y=-dp
y/p
z，即證明q
y/p
y=-d/p
z ? 畫出下面的圖來就清清楚楚了，相似三角形
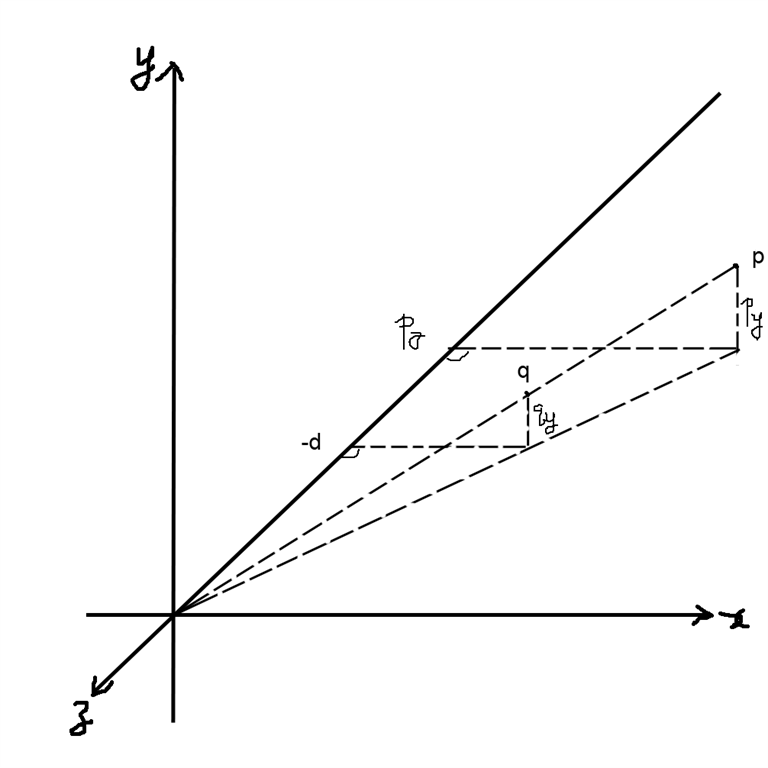
在photoshop中畫的，虛線是先畫的直線然后用橡皮間隔擦掉，汗啊！有沒有簡單的辦法？
將錐體變換為單位立方體的透視變換矩陣，書上直接給出了式(3.68)表示：
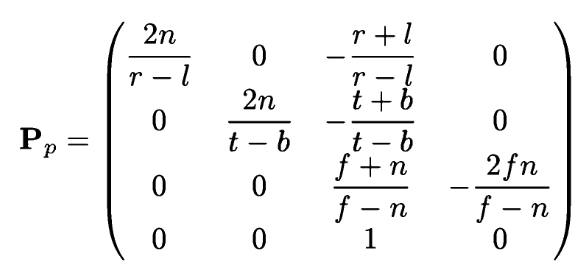
（此圖是從電子版的書上截圖下來的）
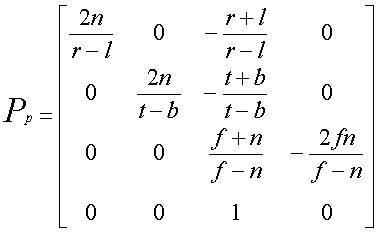（此圖是用word的公式編輯器編輯的，哇咔咔，好用啊！插入->對象->新建->Microsoft 公式 3.0）
如何推導(dǎo)出來的呢？
見丁歐南同學(xué)高一時寫的《Introduction to Perspective Projection》
看不懂的時候看下其Reference中的這個
Perspective-Correct Interpolation [Kok-Lim Low]
這個英文的更好理解 ^_^
還可以看下
| 《實時計算機圖形學(xué)(第二版)》 |
15.2 透視校正插值 |
P381 |
| 《Real-time Rendering,Second Edition》 |
15.2 Perspective-Correct Interpolation |
P680 |
| 《3D數(shù)學(xué)基礎(chǔ)：圖形與游戲開發(fā)》 |
15.3 坐標(biāo)空間 |
P326 |
| 《3D Math Primer for Graphics and Game Development》 |
15.3 Coordinate Spaces |
P354 |
2008-12-16 22:17 花了兩天時間看完了這些東西，畫滿了三張草紙的正反面，好久違的感覺啊！但是依然對透視投影很困惑 
2009-01-20 《Fundamentals of Computer Graphics》第七章 觀察 這里有比較詳細的推導(dǎo)
2010-07-05
忍不住把所有的圖片鏈接全部更新了！！！
在項目這么忙的時刻！！！
以后不斷把閱讀的體會理解都加上！
2015-07-09
今天終于把下面的推導(dǎo)都看完了，也計算了一遍。
真的不難哈，相似三角形、三角函數(shù)、齊次坐標(biāo)、矩陣，就這些而已！木有微積分和概率！
總結(jié)：時間跨度好大啊，從08年底到15年中，將近7年過去了！從26歲的青春小伙兒變成了33歲的中年大叔！空間上跨度也挺大，從上海跑到了新加坡 :) 哈哈，但不變的是一顆求知的心！
========================
透視投影（Perspective Projection）變換推導(dǎo)
透視投影是3D固定流水線的重要組成部分，是將相機空間中的點從視錐體(frustum)變換到規(guī)則觀察體(Canonical View Volume)中，待裁剪完畢后進行透視除法的行為。在算法中它是通過透視矩陣乘法和透視除法兩步完成的。
透視投影變換是令很多剛剛進入3D圖形領(lǐng)域的開發(fā)人員感到迷惑乃至神秘的一個圖形技術(shù)。其中的理解困難在于步驟繁瑣，對一些基礎(chǔ)知識過分依賴，一旦對它們中的任何地方感到陌生，立刻導(dǎo)致理解停止不前。
沒錯，主流的3D APIs如OpenGL、D3D的確把具體的透視投影細節(jié)封裝起來，比如
gluPerspective(…) 就可以根據(jù)輸入生成一個透視投影矩陣。而且在大多數(shù)情況下不需要了解具體的內(nèi)幕算法也可以完成任務(wù)。但是你不覺得，如果想要成為一個職業(yè)的圖形程序員或游戲開發(fā)者，就應(yīng)該真正降伏透視投影這個家伙么？我們先從必需的基礎(chǔ)知識著手，一步一步深入下去（這些知識在很多地方可以單獨找到，但我從來沒有在同一個地方全部找到，但是你現(xiàn)在找到了）。
我們首先介紹兩個必須掌握的知識。有了它們，我們才不至于在理解透視投影變換的過程中迷失方向（這里會使用到向量幾何、矩陣的部分知識，如果你對此不是很熟悉，可以參考
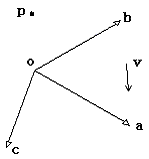
可以找到一組坐標(biāo)(v1,v2,v3)，使得
v = v1 a + v2 b + v3 c （1）
而對于一個點p，則可以找到一組坐標(biāo)（p1,p2,p3），使得
p – o = p1 a + p2 b + p3 c （2）
從上面對向量和點的表達，我們可以看出為了在坐標(biāo)系中表示一個點（如p），我們把點的位置看作是對這個基的原點o所進行的一個位移，即一個向量——p – o（有的書中把這樣的向量叫做位置向量——起始于坐標(biāo)原點的特殊向量），我們在表達這個向量的同時用等價的方式表達出了點p:
p = o + p1 a + p2 b + p3 c (3)
(1)(3)是坐標(biāo)系下表達一個向量和點的不同表達方式。這里可以看出，雖然都是用代數(shù)分量的形式表達向量和點，但表達一個點比一個向量需要額外的信息。如果我寫出一個代數(shù)分量表達(1, 4, 7)，誰知道它是個向量還是個點！
我們現(xiàn)在把（1）（3）寫成矩陣的形式：
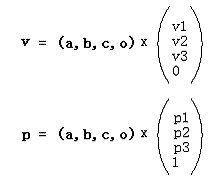
這里(a,b,c,o)是坐標(biāo)基矩陣，右邊的列向量分別是向量v和點p在基下的坐標(biāo)。這樣，向量和點在同一個基下就有了不同的表達：3D向量的第4個代數(shù)分量是0，而3D點的第4個代數(shù)分量是1。像這種這種用4個代數(shù)分量表示3D幾何概念的方式是一種齊次坐標(biāo)表示。
“齊次坐標(biāo)表示是計算機圖形學(xué)的重要手段之一，它既能夠用來明確區(qū)分向量和點，同時也更易用于進行仿射（線性）幾何變換。”—— F.S. Hill, JR
這樣，上面的(1, 4, 7)如果寫成（1,4,7,0），它就是個向量；如果是(1,4,7,1)，它就是個點。
下面是如何在普通坐標(biāo) (Ordinary Coordinate)和齊次坐標(biāo)(Homogeneous Coordinate)之間進行轉(zhuǎn)換：
從普通坐標(biāo)轉(zhuǎn)換成齊次坐標(biāo)時，
如果(x,y,z)是個點，則變?yōu)?x,y,z,1);
如果(x,y,z)是個向量，則變?yōu)?(x,y,z,0)
從齊次坐標(biāo)轉(zhuǎn)換成普通坐標(biāo)時，
如果是(x,y,z,1)，則知道它是個點，變成(x,y,z);
如果是(x,y,z,0)，則知道它是個向量，仍然變成(x,y,z)
以上是通過齊次坐標(biāo)來區(qū)分向量和點的方式。從中可以思考得知，對于平移T、旋轉(zhuǎn)R、縮放S這3個最常見的仿射變換，平移變換只對于點才有意義，因為普通向量沒有位置概念，只有大小和方向，這可以通過下面的式子清楚地看出：
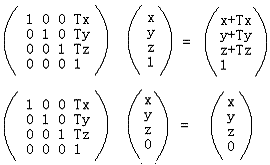
而旋轉(zhuǎn)和縮放對于向量和點都有意義，你可以用類似上面齊次表示來檢測。從中可以看出，齊次坐標(biāo)用于仿射變換非常方便。
此外，對于一個普通坐標(biāo)的點P=(Px, Py, Pz)，有對應(yīng)的一族齊次坐標(biāo)(wPx, wPy, wPz, w)，其中w不等于零。比如，P(1, 4, 7)的齊次坐標(biāo)有(1, 4, 7, 1)、（2, 8, 14, 2）、（-0.1, -0.4, -0.7, -0.1）等等。因此，如果把一個點從普通坐標(biāo)變成齊次坐標(biāo)，給x,y,z乘上同一個非零數(shù)w，然后增加第4個分量w；如果把一個齊次坐標(biāo)轉(zhuǎn)換成普通坐標(biāo)，把前三個坐標(biāo)同時除以第4個坐標(biāo)，然后去掉第4個分量。
由于齊次坐標(biāo)使用了4個分量來表達3D概念，使得平移變換可以使用矩陣進行，從而如F.S. Hill, JR所說，仿射（線性）變換的進行更加方便。由于圖形硬件已經(jīng)普遍地支持齊次坐標(biāo)與矩陣乘法，因此更加促進了齊次坐標(biāo)使用，使得它似乎成為圖形學(xué)中的一個標(biāo)準(zhǔn)。
簡單的線性插值
這是在圖形學(xué)中普遍使用的基本技巧，我們在很多地方都會用到，比如2D位圖的放大、縮小，Tweening變換，以及我們即將看到的透視投影變換等等。基本思想是：給一個x屬于[a, b]，找到y(tǒng)屬于[c, d]，使得x與a的距離比上ab長度所得到的比例，等于y與c的距離比上cd長度所得到的比例，用數(shù)學(xué)表達式描述很容易理解：
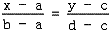
這樣，從a到b的每一個點都與c到d上的唯一一個點對應(yīng)。有一個x，就可以求得一個y。
此外，如果x不在[a, b]內(nèi)，比如x < a或者x > b，則得到的y也是符合y < c或者y > d，比例仍然不變，插值同樣適用。
透視投影變換
好，有了上面兩個理論知識，我們開始分析這次的主角——透視投影變換。這里我們選擇OpenGL的透視投影變換進行分析，其他的 APIs會存在一些差異，但主體思想是相似的，可以類似地推導(dǎo)。經(jīng)過相機矩陣的變換，頂點被變換到了相機空間。這個時候的多邊形也許會被視錐體裁剪，但在這個不規(guī)則的體中進行裁剪并非那么容易的事情，所以經(jīng)過圖形學(xué)前輩們的精心分析，裁剪被安排到規(guī)則觀察體(Canonical View Volume, CVV)中進行，CVV是一個正方體，x, y, z的范圍都是[-1，1]，多邊形裁剪就是用這個規(guī)則體完成的。所以，事實上是透視投影變換由兩步組成：
1） 用透視變換矩陣把頂點從視錐體中變換到裁剪空間的CVV中。
2） CVV裁剪完成后進行透視除法（一會進行解釋）。
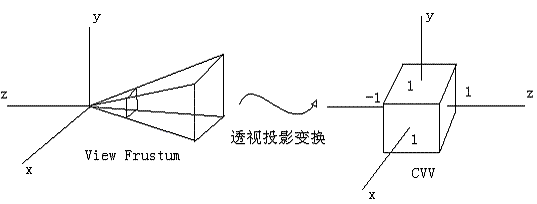
我們一步一步來，我們先從一個方向考察投影關(guān)系。
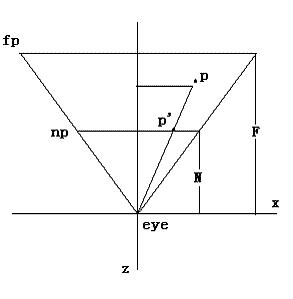
上圖是右手坐標(biāo)系中頂點在相機空間中的情形。設(shè)P(x,z)是經(jīng)過相機變換之后的點，視錐體由eye——眼睛位置，np——近裁剪平面，fp——遠裁剪平面組成。N是眼睛到近裁剪平面的距離，F(xiàn)是眼睛到遠裁剪平面的距離。投影面可以選擇任何平行于近裁剪平面的平面，這里我們選擇近裁剪平面作為投影平面。設(shè) P’(x’,z’)是投影之后的點，則有z’ = -N。通過相似三角形性質(zhì)，我們有關(guān)系：
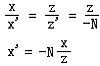
同理，有
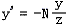
這樣，我們便得到了P投影后的點P’
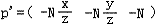
從上面可以看出，投影的結(jié)果z’始終等于-N，在投影面上。實際上，z’對于投影后的P’已經(jīng)沒有意義了，這個信息點已經(jīng)沒用了。但對于3D圖形管線來說，為了便于進行后面的片元操作，例如z緩沖消隱算法，有必要把投影之前的z保存下來，方便后面使用。因此，我們利用這個沒用的信息點存儲z，處理成：
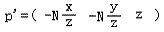
這個形式最大化地使用了3個信息點，達到了最原始的投影變換的目的，但是它太直白了，有一點蠻干的意味，我感覺我們最終的結(jié)果不應(yīng)該是它，你說呢？我們開始結(jié)合CVV進行思考，把它寫得在數(shù)學(xué)上更優(yōu)雅一致，更易于程序處理。假入能夠把上面寫成這個形式：
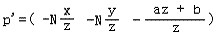
那么我們就可以非常方便的用矩陣以及齊次坐標(biāo)理論來表達投影變換：
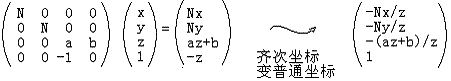
其中
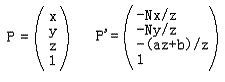
哈，看到了齊次坐標(biāo)的使用，這對于你來說已經(jīng)不陌生了吧？這個新的形式不僅達到了上面原始投影變換的目的，而且使用了齊次坐標(biāo)理論，使得處理更加規(guī)范化。注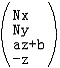意在把 
變成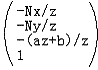
的一步我們是使用齊次坐標(biāo)變普通坐標(biāo)的規(guī)則完成的。這一步在透視投影過程中稱為透視除法（Perspective Division），這是透視投影變換的第2步，經(jīng)過這一步，就丟棄了原始的z值（得到了CVV中對應(yīng)的z值，后面解釋），頂點才算完成了投影。而在這兩步之間的就是CVV裁剪過程，所以裁剪空間使用的是齊次坐標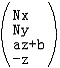(biāo) ，主要原因在于透視除法會損失一些必要的信息（如原始z，第4個-z保留的）從而使裁剪變得更加難以處理，這里我們不討論CVV裁剪的細節(jié)，只關(guān)注透視投影變換的兩步。
矩陣
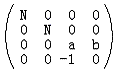
就是我們投影矩陣的第一個版本。你一定會問為什么要把z寫成
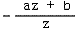
有兩個原因：
1） P’的3個代數(shù)分量統(tǒng)一地除以分母-z，易于使用齊次坐標(biāo)變?yōu)槠胀ㄗ鴺?biāo)來完成，使得處理更加一致、高效。
2） 后面的CVV是一個x,y,z的范圍都為[-1，1]的規(guī)則體，便于進行多邊形裁剪。而我們可以適當(dāng)?shù)倪x擇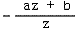系數(shù)a和b，使得 這個式子在z = -N的時候值為-1，而在z = -F的時候值為1，從而在z方向上構(gòu)建CVV。
接下來我們就求出a和b：
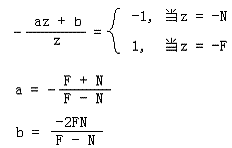
這樣我們就得到了透視投影矩陣的第一個版本：
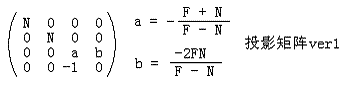
使用這個版本的透視投影矩陣可以從z方向上構(gòu)建CVV，但是x和y方向仍然沒有限制在[-1,1]中，我們的透視投影矩陣的下一個版本就要解決這個問題。
為了能在x和y方向把頂點從Frustum情形變成CVV情形，我們開始對x和y進行處理。先來觀察我們目前得到的最終變換結(jié)果：
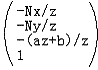
我們知道-Nx / z的有效范圍是投影平面的左邊界值（記為left）和右邊界值（記為right），即[left, right]，-Ny / z則為[bottom, top]。而現(xiàn)在我們想把-Nx / z屬于[left, right]映射到x屬于[-1, 1]中，-Ny / z屬于[bottom, top]映射到y(tǒng)屬于[-1, 1]中。你想到了什么？哈，就是我們簡單的線性插值，你都已經(jīng)掌握了！我們解決掉它：
則我們得到了最終的投影點：
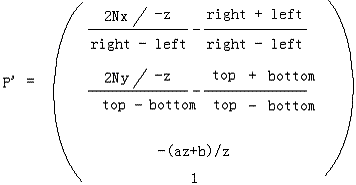
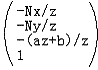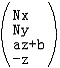下面要做的就是從這個新形式出發(fā)反推出下一個版本的透視投影矩陣。注意到 是 經(jīng)過透視除法的形式，而P’只變化了x和y分量的形式，az+b和-z是不變的，則我們做透視除法的逆處理——給P’每個分量乘上-z，得到
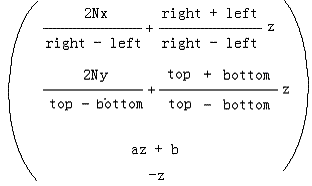
而這個結(jié)果又是這么來的：
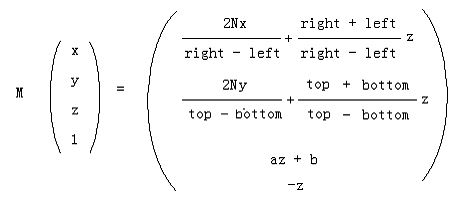
則我們最終得到：
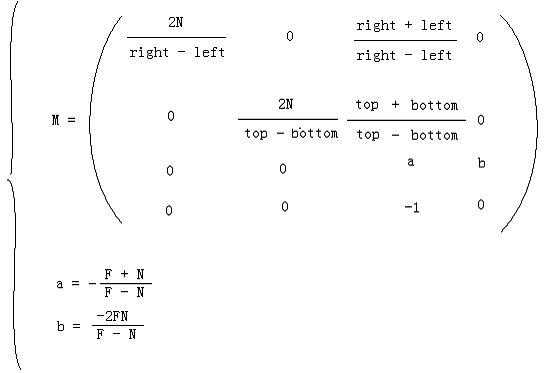
M 就是最終的透視變換矩陣。相機空間中的頂點，如果在視錐體中，則變換后就在CVV中。如果在視錐體外，變換后就在CVV外。而CVV本身的規(guī)則性對于多邊形的裁剪很有利。OpenGL在構(gòu)建透視投影矩陣的時候就使用了M的形式。注意到M的最后一行不是(0 0 0 1)而是(0 0 -1 0)，因此可以看出透視變換不是一種仿射變換，它是非線性的。另外一點你可能已經(jīng)想到，對于投影面來說，它的寬和高大多數(shù)情況下不同，即寬高比不為1，比如640/480。而CVV的寬高是相同的，即寬高比永遠是1。這就造成了多邊形的失真現(xiàn)象，比如一個投影面上的正方形在CVV的面上可能變成了一個長方形。解決這個問題的方法就是在對多變形進行透視變換、裁剪、透視除法之后，在歸一化的設(shè)備坐標(biāo)(Normalized Device Coordinates)上進行的視口(viewport)變換中進行校正，它會把歸一化的頂點之間按照和投影面上相同的比例變換到視口中，從而解除透視投影變換帶來的失真現(xiàn)象。進行校正前提就是要使投影平面的寬高比和視口的寬高比相同。
便利的投影矩陣生成函數(shù)
3D APIs都提供了諸如gluPerspective(fov, aspect, near, far)或者D3DXMatrixPerspectiveFovLH(pOut, fovY, Aspect, zn, zf)這樣的函數(shù)為用戶提供快捷的透視矩陣生成方法。我們還是用OpenGL的相應(yīng)方法來分析它是如何運作的。
gluPerspective(fov, aspect, near, far)
fov即視野，是視錐體在xz平面或者yz平面的開角角度，具體哪個平面都可以。OpenGL和 D3D都使用yz平面。
aspect即投影平面的寬高比。
near是近裁剪平面的距離
far是遠裁剪平面的距離。
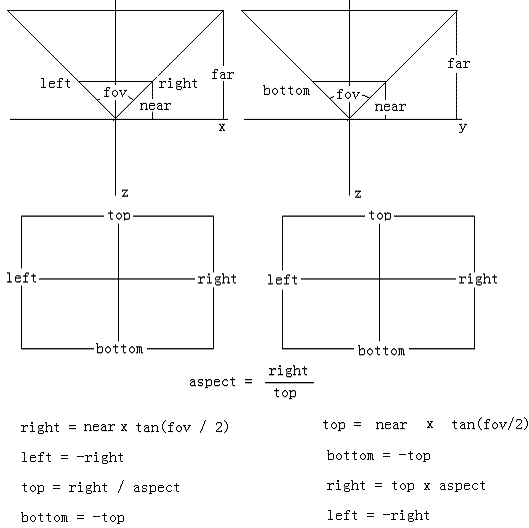
上圖中左邊是在xz平面計算視錐體，右邊是在yz平面計算視錐體。可以看到左邊的第3步top = right / aspect使用了除法（圖形程序員討厭的東西），而右邊第3步right = top x aspect使用了乘法，這也許就是為什么圖形APIs采用yz平面的原因吧！
posted on 2008-12-15 18:44
七星重劍 閱讀(10774)
評論(7) 編輯 收藏 引用 所屬分類:
Game Graphics