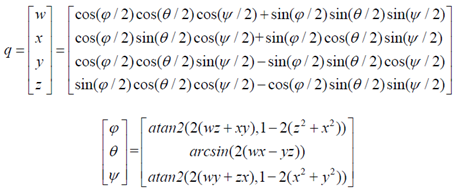本文乃轉(zhuǎn)載,但原文地址不知。若作者有幸看到,請及時認領(lǐng)。
在3D圖形學中,最常用的旋轉(zhuǎn)表示方法便是四元數(shù)和歐拉角,比起矩陣來具有節(jié)省存儲空間和方便插值的優(yōu)點。本文主要歸納了兩種表達方式的轉(zhuǎn)換,計算公式采用3D笛卡爾坐標系:
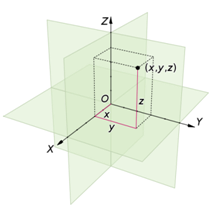
圖1 3D Cartesian coordinate System (from wikipedia)
定義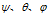 分別為繞Z軸、Y軸、X軸的旋轉(zhuǎn)角度,如果用Tait-Bryan angle表示,分別為Yaw、Pitch、Roll。
分別為繞Z軸、Y軸、X軸的旋轉(zhuǎn)角度,如果用Tait-Bryan angle表示,分別為Yaw、Pitch、Roll。
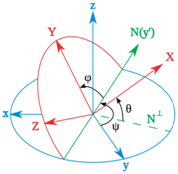
圖2 Tait-Bryan angles (from wikipedia)
一、四元數(shù)的定義
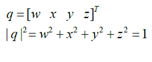
通過旋轉(zhuǎn)軸和繞該軸旋轉(zhuǎn)的角度可以構(gòu)造一個四元數(shù):
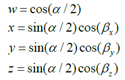
其中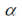 是繞旋轉(zhuǎn)軸旋轉(zhuǎn)的角度,
是繞旋轉(zhuǎn)軸旋轉(zhuǎn)的角度,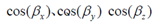 為旋轉(zhuǎn)軸在x,y,z方向的分量(由此確定了旋轉(zhuǎn)軸)。
為旋轉(zhuǎn)軸在x,y,z方向的分量(由此確定了旋轉(zhuǎn)軸)。
二、歐拉角到四元數(shù)的轉(zhuǎn)換
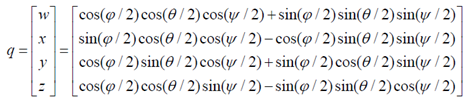
三、四元數(shù)到歐拉角的轉(zhuǎn)換

arctan和arcsin的結(jié)果是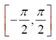 ,這并不能覆蓋所有朝向(對于
,這并不能覆蓋所有朝向(對于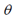 角
角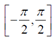 的取值范圍已經(jīng)滿足),因此需要用atan2來代替arctan。
的取值范圍已經(jīng)滿足),因此需要用atan2來代替arctan。
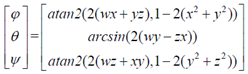
四、在其他坐標系下使用
在其他坐標系下,需根據(jù)坐標軸的定義,調(diào)整一下以上公式。如在Direct3D中,笛卡爾坐標系的X軸變?yōu)閆軸,Y軸變?yōu)閄軸,Z軸變?yōu)閅軸(無需考慮方向)。