一直以來,我都記不住向量叉乘的結果,每次都要查詢。其根本原因在于,我沒有去研究過叉乘是如何推導出來的。于是,這次想徹底解決一下。首先要感謝維基百科,它已經把所有問題都描述清楚了。
http://en.wikipedia.org/wiki/Cross_product
而下面的文字,只是我的讀書筆記,以加深自己的印象。
首先我們知道 ,對于向量u和v, u x v的結果,是得到一個既垂直于u又垂直于v的向量,假設記作n.
則有下面公式
n = u x v;
而n的方向,是由右手法則決定的。 即伸出右手,四個手指方向從u繞到v. 此時,大姆指的方向,就是n的方向。 我們通常叫做右向量。
引用一下維基百科的圖來說明問題,有興趣的兄弟可以照圖比劃一下。 (注:圖中向量是用的a x b來表示)
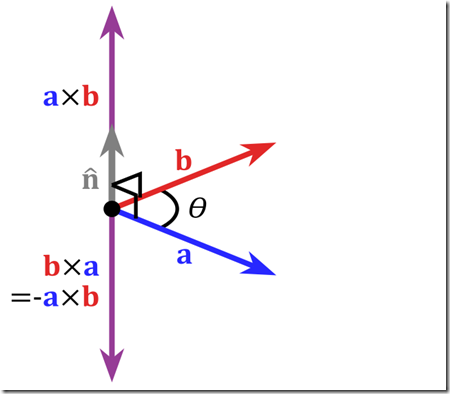
有了上面的知識,我們繼續向下看。
我們假設向量 u,v,n分別用三個標量來表示。即
u = (Xu,Yu,Zu)
v = (Xv,Yv,Zv)
n = (Xn,Yn,Zn)
則,它們的關系為
Xn = Yu*Zv – Zu*Yv;
Yn = Zu*Xv – Xu*Zv;
Zn = Xu*Yv – Yu*Xv;
即 n = (Yu*Zv – Zu*Yv,Zu*Xv – Xu*Zv,Xu*Yv – Yu*Xv);
而為了驗證n與u和v的垂直性,可以使用點乘進行
點乘法則比這個簡單多了, u*v = (Xu*Xv + Yu*Yv + Zu*Zv) = dotUV;
如果兩個向量垂直,則dotUV = 0;
代入驗證一把
u*n = (Xu*(Yu*Zv – Zu*Yv) + Yu*(Zu*Xv – Xu*Zv) + Zu*(Xu*Yv – Yu*Xv));
= Xu*Yu*Zv – Xu*Zu*Yv + Yu*Zu*Xv – Yu*Xu*Zv + Zu*Xu*Yv – Zu*Yu*Xv;
把正負號的因式仔細比對一下,發現剛好可以低消。 結果為0.
v*n 同理可證。
于是,也驗證了n與u,v垂直的特性。
如果只是為了應用的話,走到這一步就可以停下了。后面的知識,只是為了滿足一下好奇心。
那我們就來看看,這個結論是怎么來的呢? 我們接著來推導。
為了更好地推導,我們需要加入三個軸對齊的單位向量。
i,j,k.
i,j,k滿足以下特點
i = j x k; j = k x i; k = i x j;
k x j = –i; i x k = –j; j x i = –k;
i x i = j x j = k x k = 0; (0是指0向量)
由此可知,i,j,k是三個相互垂直的向量。它們剛好可以構成一個坐標系。
這三個向量的特例就是 i = (1,0,0) j = (0,1,0) k = (0,0,1)。
好,那對于處于i,j,k構成的坐標系中的向量u,v我們可以如下表示
u = Xu*i + Yu*j + Zu*k;
v = Xv*i + Yv*j + Zv*k;
那么 u x v = (Xu*i + Yu*j + Zu*k) x (Xv*i + Yv*j + Zv*k)
= Xu*Xv*(ixi) + Xu*Yv*(i x j) + Xu*Zv*(i x k) + Yu*Xv*(j x i) + Yu*Yv*(j x j) + Yu*Zv*(j x k) + Zu*Xv*( k x i ) + Zu*Yv(k x j) + Zu*Zv(k x k)
由于上面的i,j,k三個向量的特點,所以,最后的結果可以簡化為
u x v = (Yu*Zv – Zu*Yv)*i + (Zu*Xv – Xu*Zv)j + (Xu*Yv – Yu*Xv)k;
于是,在i,j,k構成的坐標系中。集就是上面的結果。
當i = (1,0,0) j = (0,1,0) k = (0,0,1)時,我們通常省略i,j,k的寫法。最終也就得到了我們的右向量。
叉乘的意義
叉乘表示垂直于uxv的右向量。
使用的地方
可以通過叉乘,修正向量關系,從而構建坐標系。 常見的有 攝相機矩陣和TBN空間轉換矩陣的構建。
叉乘的矩陣表示法。
很多書上,包括 3D游戲大師編程技巧 上面,都是用的矩陣表示法來說明叉乘。
如下。
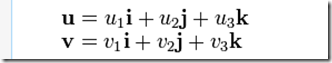
它對應的矩陣表示法為
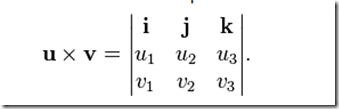
求其代數余子式,可以表示為如下
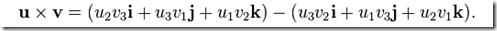
有了這個,那我們合并公因式i,j,k,則可以得到矩陣表示法
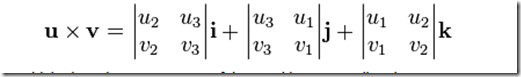
到此,叉乘的內容基本OK了。 值得說明的是,如果對方程組表示成矩陣不熟悉,就會感到不習慣,但是如果多多練習,我想應該是會習慣成自然吧。。。