左手坐標系的直觀表示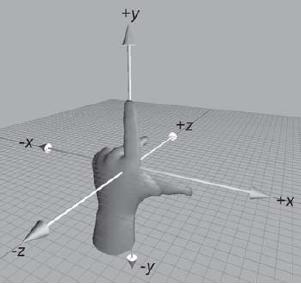：  向量的表示（軸對齊包圍盒（AABB（axially aligned bounding box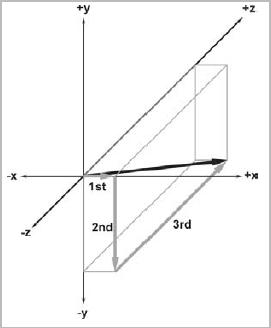）））：  2D向量的長度： ||v|| = sqrt(vx*vx + vy*vy)3D向量的長度： ||v|| = sqrt(vx*vx + vy*vy + vz*vz)
標準化向量＝此向量/此向量的長度＝vx / ||v|| , vy / ||v|| , vz / ||v||
標準化后的向量的頭接觸到圓心在原點的單位圓（單位圓的半徑為1）
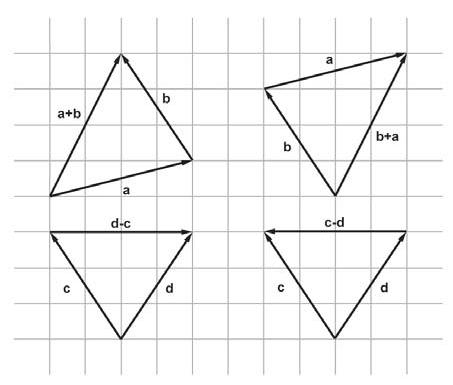
向量加法的幾何意義（三角形法則）：
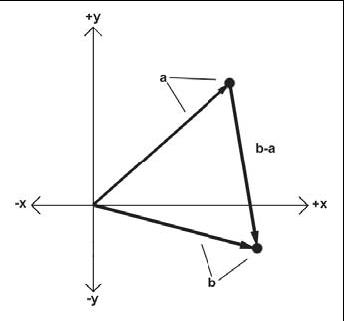
計算一個點到另一個點的位移可以使用三角形法則和向量減法來解決這個問題:
兩點間距離的公式：設(shè)兩點分別為3D向量a和b
則距離（a，b）=||b-a||=sqrt((bx - ax)2 +(by - ay)2 +(bz - az)2 )
向量點乘：點乘等于向量大小與向量夾角的cos值的積，其中c為兩點a和b的夾角：
a點乘b=||a||*||b||*cos(c)
計算向量的夾角：c =acos( (a*b)/(||a|| * ||b||))
如果a和b是單位向量，則c=acos(a*b)
當點乘結(jié)果大于0，則夾角小于90度
當點乘結(jié)果等于0，則夾角等于90度
當點乘結(jié)果小于0，則夾角大于90度
向量差乘：
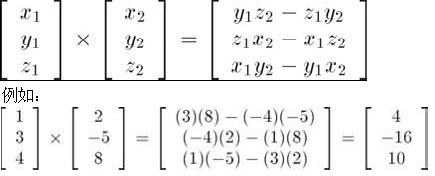
向量的封裝類：
  /**////////////////////////////////////////////////////////////////////////////// //
//?3D?Math?Primer?for?Games?and?Graphics?Development
//
//?Vector3.h?-?Declarations?for?3D?vector?class
//
//?Visit?gamemath.com?for?the?latest?version?of?this?file.
//
//?For?additional?comments,?see?Chapter?6.
//
/**//////////////////////////////////////////////////////////////////////////////
#ifndef?__VECTOR3_H_INCLUDED__
#define?__VECTOR3_H_INCLUDED__
#include?<math.h>
/**////////////////////////////////////////////////////////////////////////////////
//?class?Vector3?-?a?simple?3D?vector?class
//
/**//////////////////////////////////////////////////////////////////////////////
class?Vector3? {
 public:
//?Public?representation:??Not?many?options?here.
????float?x,y,z;
//?Constructors
????//?Default?constructor?leaves?vector?in
????//?an?indeterminate?state
  ????Vector3()?{}
????//?Copy?constructor
????Vector3(const?Vector3?&a)?:?x(a.x),?y(a.y),?z(a.z)?{}
????//?Construct?given?three?values
????Vector3(float?nx,?float?ny,?float?nz)?:?x(nx),?y(ny),?z(nz)?{}
//?Standard?object?maintenance
????//?Assignment.??We?adhere?to?C?convention?and
????//?return?reference?to?the?lvalue
????Vector3?&operator?=(const?Vector3?&a)?{
????????x?=?a.x;?y?=?a.y;?z?=?a.z;
????????return?*this;
 ????}
????//?Check?for?equality
????bool?operator?==(const?Vector3?&a)?const?{
????????return?x==a.x?&&?y==a.y?&&?z==a.z;
????}
????bool?operator?!=(const?Vector3?&a)?const?{
????????return?x!=a.x?||?y!=a.y?||?z!=a.z;
????}
//?Vector?operations
????//?Set?the?vector?to?zero
????void?zero()?{?x?=?y?=?z?=?0.0f;?}
????//?Unary?minus?returns?the?negative?of?the?vector
????Vector3?operator?-()?const?{?return?Vector3(-x,-y,-z);?}
????//?Binary?+?and?-?add?and?subtract?vectors
????Vector3?operator?+(const?Vector3?&a)?const?{
????????return?Vector3(x?+?a.x,?y?+?a.y,?z?+?a.z);
????}
????Vector3?operator?-(const?Vector3?&a)?const?{
????????return?Vector3(x?-?a.x,?y?-?a.y,?z?-?a.z);
????}
????//?Multiplication?and?division?by?scalar
????Vector3?operator?*(float?a)?const?{
????????return?Vector3(x*a,?y*a,?z*a);
????}
????Vector3?operator?/(float?a)?const?{
????????float????oneOverA?=?1.0f?/?a;?//?NOTE:?no?check?for?divide?by?zero?here
????????return?Vector3(x*oneOverA,?y*oneOverA,?z*oneOverA);
????}
????//?Combined?assignment?operators?to?conform?to
????//?C?notation?convention
????Vector3?&operator?+=(const?Vector3?&a)?{
????????x?+=?a.x;?y?+=?a.y;?z?+=?a.z;
????????return?*this;
????}
????Vector3?&operator?-=(const?Vector3?&a)?{
????????x?-=?a.x;?y?-=?a.y;?z?-=?a.z;
????????return?*this;
????}
????Vector3?&operator?*=(float?a)?{
????????x?*=?a;?y?*=?a;?z?*=?a;
????????return?*this;
????}
????Vector3?&operator?/=(float?a)?{
????????float????oneOverA?=?1.0f?/?a;
????????x?*=?oneOverA;?y?*=?oneOverA;?z?*=?oneOverA;
????????return?*this;
????}
????//?Normalize?the?vector
????void????normalize()?{
????????float?magSq?=?x*x?+?y*y?+?z*z;
????????if?(magSq?>?0.0f)?{?//?check?for?divide-by-zero
????????????float?oneOverMag?=?1.0f?/?sqrt(magSq);
????????????x?*=?oneOverMag;
????????????y?*=?oneOverMag;
????????????z?*=?oneOverMag;
????????}
????}
????//?Vector?dot?product.??We?overload?the?standard
????//?multiplication?symbol?to?do?this
????float?operator?*(const?Vector3?&a)?const?{
????????return?x*a.x?+?y*a.y?+?z*a.z;
????}
 };
/**////////////////////////////////////////////////////////////////////////////////
//?Nonmember?functions
//
/**//////////////////////////////////////////////////////////////////////////////
//?Compute?the?magnitude?of?a?vector
inline?float?vectorMag(const?Vector3?&a)?{
????return?sqrt(a.x*a.x?+?a.y*a.y?+?a.z*a.z);
}
//?Compute?the?cross?product?of?two?vectors
inline?Vector3?crossProduct(const?Vector3?&a,?const?Vector3?&b)?{
????return?Vector3(
????????a.y*b.z?-?a.z*b.y,
????????a.z*b.x?-?a.x*b.z,
????????a.x*b.y?-?a.y*b.x
????);
}
//?Scalar?on?the?left?multiplication,?for?symmetry
inline?Vector3?operator?*(float?k,?const?Vector3?&v)?{
????return?Vector3(k*v.x,?k*v.y,?k*v.z);
}
//?Compute?the?distance?between?two?points
inline?float?distance(const?Vector3?&a,?const?Vector3?&b)?{
????float?dx?=?a.x?-?b.x;
????float?dy?=?a.y?-?b.y;
????float?dz?=?a.z?-?b.z;
????return?sqrt(dx*dx?+?dy*dy?+?dz*dz);
}
//?Compute?the?distance?between?two?points,?squared.??Often?useful
//?when?comparing?distances,?since?the?square?root?is?slow
inline?float?distanceSquared(const?Vector3?&a,?const?Vector3?&b)?{
????float?dx?=?a.x?-?b.x;
????float?dy?=?a.y?-?b.y;
????float?dz?=?a.z?-?b.z;
????return?dx*dx?+?dy*dy?+?dz*dz;
}
/**////////////////////////////////////////////////////////////////////////////////
//?Global?variables
//
/**//////////////////////////////////////////////////////////////////////////////
//?We?provide?a?global?zero?vector?constant
extern?const?Vector3?kZeroVector;
/**//////////////////////////////////////////////////////////////////////////////#endif?//?#ifndef?__VECTOR3_H_INCLUDED__
|