Topology Shapes of OpenCascade BRep
eryar@163.com
摘要Abstract：通過(guò)對(duì)OpenCascade中的BRep數(shù)據(jù)的讀寫(xiě)，理解邊界表示法的概念及實(shí)現(xiàn)。理解了拓樸形狀的數(shù)據(jù)結(jié)構(gòu)，就對(duì)ModelingData模塊有了清晰認(rèn)識(shí)，方便OpenCascade其他模塊如ModelingAlgorithms和Visiualization模塊的理解。
關(guān)鍵字Key Words：OpenCascade, BRep, Topology, BRep Format
一、引言 Introduction
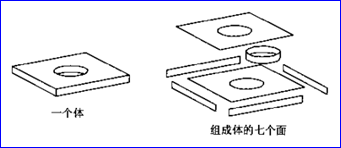
邊界表示（Boundary Representation）也稱(chēng)為BRep表示，它是幾何造型中最成熟、無(wú)二義的表示法。實(shí)體的邊界通常是由面的并集表示，而每個(gè)面又由它所在曲面的定義加上其邊界來(lái)表示，面的邊界是邊的并集，而邊又是由點(diǎn)來(lái)表示。如下圖1.1所示，曲面的匯合處形成曲線，而曲線的匯合處形成點(diǎn)。所以點(diǎn)、線、面是描述一個(gè)形狀所需要的基本組成單元。
Figure 1.1 BRep Shape demo
邊界表示的一個(gè)重要特點(diǎn)是描述形狀的信息包括幾何信息（geometry）和拓樸（topology）信息兩個(gè)方面。拓樸信息描述形狀上的頂點(diǎn)、邊、面的連接關(guān)系，它形成物體邊界表示的“骨架”。形狀的幾何信息猶如附著在“骨架”上的肌肉。在OpenCascade中，形狀的幾何信息包含曲線和曲面的參數(shù)解析表示Geom_Curve/Geom_Surface。
這樣我們就可以用平面方程和柱面方程來(lái)描述曲面，用直線或圓弧方程來(lái)描述曲線。這時(shí)會(huì)出現(xiàn)一個(gè)問(wèn)題，即代數(shù)表達(dá)式只能定義無(wú)邊界的幾何體。除了單個(gè)點(diǎn)、圓以及球體，經(jīng)典的解析幾何僅能表示無(wú)限延伸的曲線和曲面。為了解決這個(gè)問(wèn)題，邊界表示法按下述方法明確地定義曲線或曲面的邊界：
l 曲線的邊界由位于曲線上的一對(duì)點(diǎn)來(lái)確定；
l 曲面的邊界由位于曲面上的一組曲線來(lái)確定；
通過(guò)這個(gè)方法，就可以定義一段曲線或一片曲面。這時(shí)，不同幾何元素之間的關(guān)系的組織問(wèn)題就出現(xiàn)了，為此我們將記錄如下信息：
l 哪些點(diǎn)界定哪些曲線；
l 哪些曲線界定哪些曲面；
這些關(guān)于誰(shuí)關(guān)聯(lián)誰(shuí)的信息，就是幾何造型系統(tǒng)經(jīng)常提到的拓樸。在邊界表示法中，理論上表示一個(gè)物理模型只需要三個(gè)拓樸體（頂點(diǎn)TopoDS_Vertex、邊TopoDS_Edge和面TopoDS_Face），但在實(shí)際應(yīng)用中，為了提高計(jì)算機(jī)處理的速度或提供高級(jí)的操作功能，還要引入其他一些概念，如環(huán)TopoDS_Wire、殼TopoDS_Shell、復(fù)合體TopoDS_Compound等。
二、邊界表示形狀中的幾何數(shù)據(jù) Geometry of BRep shapes
對(duì)形狀數(shù)據(jù)的讀寫(xiě)主要是由類(lèi)BRepTools_ShapeSet來(lái)完成的，其中在類(lèi)的函數(shù)AddGeometry中對(duì)拓樸形狀中的幾何數(shù)據(jù)進(jìn)行了處理，代碼如下所示：
//=================================================================
//function : AddGeometry
//purpose :
//=================================================================
void BRepTools_ShapeSet::AddGeometry(const TopoDS_Shape& S)
{
// Add the geometry
if (S.ShapeType() == TopAbs_VERTEX) {
Handle(BRep_TVertex) TV = Handle(BRep_TVertex)::DownCast(S.TShape());
BRep_ListIteratorOfListOfPointRepresentation itrp(TV->Points());
while (itrp.More()) {
const Handle(BRep_PointRepresentation)& PR = itrp.Value();
if (PR->IsPointOnCurve()) {
myCurves.Add(PR->Curve());
}
else if (PR->IsPointOnCurveOnSurface()) {
myCurves2d.Add(PR->PCurve());
mySurfaces.Add(PR->Surface());
}
else if (PR->IsPointOnSurface()) {
mySurfaces.Add(PR->Surface());
}
ChangeLocations().Add(PR->Location());
itrp.Next();
}
}
else if (S.ShapeType() == TopAbs_EDGE) {
// Add the curve geometry
Handle(BRep_TEdge) TE = Handle(BRep_TEdge)::DownCast(S.TShape());
BRep_ListIteratorOfListOfCurveRepresentation itrc(TE->Curves());
while (itrc.More()) {
const Handle(BRep_CurveRepresentation)& CR = itrc.Value();
if (CR->IsCurve3D()) {
if (!CR->Curve3D().IsNull()) {
myCurves.Add(CR->Curve3D());
ChangeLocations().Add(CR->Location());
}
}
else if (CR->IsCurveOnSurface()) {
mySurfaces.Add(CR->Surface());
myCurves2d.Add(CR->PCurve());
ChangeLocations().Add(CR->Location());
if (CR->IsCurveOnClosedSurface())
myCurves2d.Add(CR->PCurve2());
}
else if (CR->IsRegularity()) {
mySurfaces.Add(CR->Surface());
ChangeLocations().Add(CR->Location());
mySurfaces.Add(CR->Surface2());
ChangeLocations().Add(CR->Location2());
}
else if (myWithTriangles) { // for XML Persistence
if (CR->IsPolygon3D()) {
if (!CR->Polygon3D().IsNull()) {
myPolygons3D.Add(CR->Polygon3D());
ChangeLocations().Add(CR->Location());
}
}
else if (CR->IsPolygonOnTriangulation()) {
myTriangulations.Add(CR->Triangulation());
myNodes.Add(CR->PolygonOnTriangulation());
ChangeLocations().Add(CR->Location());
if (CR->IsPolygonOnClosedTriangulation())
myNodes.Add(CR->PolygonOnTriangulation2());
}
else if (CR->IsPolygonOnSurface()) {
mySurfaces.Add(CR->Surface());
myPolygons2D.Add(CR->Polygon());
ChangeLocations().Add(CR->Location());
if (CR->IsPolygonOnClosedSurface())
myPolygons2D.Add(CR->Polygon2());
}
}
itrc.Next();
}
}
else if (S.ShapeType() == TopAbs_FACE) {
// Add the surface geometry
Handle(BRep_TFace) TF = Handle(BRep_TFace)::DownCast(S.TShape());
if (!TF->Surface().IsNull()) mySurfaces.Add(TF->Surface());
if (myWithTriangles) { // for XML Persistence
Handle(Poly_Triangulation) Tr = TF->Triangulation();
if (!Tr.IsNull()) myTriangulations.Add(Tr);
}
ChangeLocations().Add(TF->Location());
}
}
根據(jù)上述代碼可知，OpenCascade在保存和讀寫(xiě)B(tài)Rep表示的形狀時(shí)，只保存了頂點(diǎn)、邊和面的信息，因?yàn)橹挥羞@三個(gè)拓樸結(jié)構(gòu)中包含了幾何信息及顯示用的離散點(diǎn)和三角網(wǎng)格數(shù)據(jù)。有了這些信息，就可以生成一個(gè)邊界表示的形狀了。
幾何之間的聯(lián)系也保存起來(lái)了，這也是拓樸數(shù)據(jù)的一種形式，在下節(jié)詳細(xì)說(shuō)明。
三、邊界表示形狀中的拓樸數(shù)據(jù) Topology of BRep shapes
關(guān)于拓樸頂點(diǎn)TopoDS_Vertex、邊TopoDS_Edge、面TopoDS_Face更詳細(xì)的信息，請(qǐng)參考博客：
l Topology and Geometry in OpenCascade-Vertex;
l Topology and Geometry in OpenCascade-Edge;
l Topology and Geometry in OpenCascade-Face;
l Topology and Geometry in OpenCascade-Topology;
本文只對(duì)OpenCascade拓樸結(jié)構(gòu)中的幾何數(shù)據(jù)的關(guān)聯(lián)信息進(jìn)行分析。
3.1 頂點(diǎn) TopoDS_Vertex
結(jié)合《BRep Format Description White Paper》中對(duì)<vertex data>的描述，及程序代碼中對(duì)頂點(diǎn)數(shù)據(jù)的讀取，分析OpenCascade的BRep表示中的頂點(diǎn)。
Figure 3.1.1 NBF-like definition of Vertex
詳細(xì)說(shuō)明：
<vertex data representation u parameter>u的使用方法說(shuō)明如下：
<vertex data representation data 1> 和參數(shù)u定義了三維曲線C上的點(diǎn)V的位置。參數(shù)u是曲線C上點(diǎn)V對(duì)應(yīng)的參數(shù)：C（u）＝V。對(duì)應(yīng)的類(lèi)是：BRep_PointOnCurve；
<vertex data representation data 2>和參數(shù)u定義了曲面上的二維曲線C上點(diǎn)V的位置。參數(shù)u是曲線C上點(diǎn)V對(duì)應(yīng)的參數(shù)：C（u）＝V。對(duì)應(yīng)的類(lèi)是：BRep_PointOnCurveOnSurface；
<vertex data representation data 3>和參數(shù)u及<vertex data representation v parameter>v定義了曲面S上的點(diǎn)V：S（u，v）＝V。對(duì)應(yīng)的類(lèi)是：BRep_PointOnSurface；
在這些類(lèi)中都將頂點(diǎn)對(duì)應(yīng)的曲線、曲面及其上點(diǎn)的參數(shù)都保存起來(lái)了。有了這些信息就可以判斷與頂點(diǎn)有聯(lián)系的邊或面，因?yàn)榍€、曲面屬于邊和面。
<vertex data tolerance>t定義如下所示：
下面結(jié)合程序示例片段，創(chuàng)建一個(gè)頂點(diǎn)并將其輸出為BRep文件，并在OpenCascade中進(jìn)行顯示。
void TestVertex(void)
{
ofstream dumpFile("vertex.brep");
TopoDS_Vertex aVertex = BRepBuilderAPI_MakeVertex(gp_Pnt(1.0, 2.0, 3.0));
BRepTools::Dump(aVertex, std::cout);
BRepTools::Write(aVertex, dumpFile);
}
當(dāng)使用BRepTools::Dump時(shí)，顯示更易讀的信息。可將數(shù)據(jù)dump到屏幕，也可將數(shù)據(jù)dump到文件；當(dāng)使用Write時(shí)，生成的信息即是BRep文件格式的數(shù)據(jù)。可以通過(guò)Read生成形狀，也可直接讀入到OpenCascade中顯示，如下圖3.1.2所示：
Figure 3.1.2 Import a Vertex from brep file
3.2 邊 TopoDS_Edge
詳細(xì)說(shuō)明：
標(biāo)志位<edge data same parameter flag>，<edge data same range flag>，<edge data degenerated flag>有特別的用途。
<edge data representation data 1>表示一個(gè)三維曲線，對(duì)應(yīng)類(lèi)：Geom_Curve；
<edge data representation data 2>表示曲面上的一個(gè)二維曲線，
對(duì)應(yīng)類(lèi)Geom_Curve/Geom_Surface；
<curve values for parameter minimal and maximal values>只在2版本中使用；
<edge data representation data 3>表示閉合曲面上的一個(gè)二維曲線；
對(duì)應(yīng)類(lèi)Geom_Curve/Geom_Surface；
<curve values for parameter minimal and maximal values>只在2版本中使用；
<edge data representation data 4>表示Regularity的邊，使用到的類(lèi)有：
Geom_Curve/Geom_Surface；
<edge data representation data 5>表示一個(gè)三維的多段線（3D polyline）；
對(duì)應(yīng)的類(lèi)：Poly_Polygon3D，是邊的近似表示，主要用來(lái)顯示；
<edge data representation data 6>表示三角剖分上一條多段線；
對(duì)應(yīng)的類(lèi)：Poly_PolygonOnTriangulation，也是邊在三角剖分上的近似表示；
<edge data tolerance> t的定義如下所示：
下面的示例程序片段將圓的邊導(dǎo)出為BRep文件，并在OpenCascade中顯示。程序代碼如下所示：
void TestEdge(bool bSubdivision = false)
{
ofstream dumpFile("edge.brep");
TopoDS_Edge anEdge = BRepBuilderAPI_MakeEdge(gp_Circ(gp::XOY(), 6.0));
if (bSubdivision)
{
BRepMesh::Mesh(anEdge, 1.0);
}
BRepTools::Dump(anEdge, std::cout);
BRepTools::Write(anEdge, dumpFile);
}
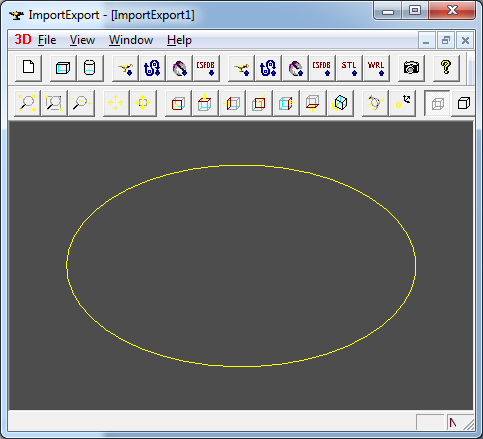
其中參數(shù)bSubdivision用來(lái)生成顯示用的離散多段線數(shù)據(jù)，這里會(huì)生成<edge data representation data 5>的Poly_Polygon3D，將生成的BRep文件導(dǎo)入進(jìn)行顯示如下圖所示：
Figure 3.2.1 Import a Face from brep file
3.3 面 TopoDS_Face
詳細(xì)說(shuō)明：
<face data>描述了面F的曲面S和三角剖分T。曲面S可能為空：<surface number>＝0.
<face data tolerance> t的定義如下所示：
標(biāo)志位<face data natural restriction flag>有特別的用途。
面中的數(shù)據(jù)比較簡(jiǎn)單，有參數(shù)表示的曲面的索引號(hào)。若曲面已經(jīng)被三角剖分，將會(huì)把剖分后的網(wǎng)格數(shù)據(jù)也保存起來(lái)。下面的示例程序片段將一個(gè)球面導(dǎo)出為brep文件：
void TestFace(bool bSubdivision = false)
{
ofstream dumpFile("face.brep");
TopoDS_Face aFace = BRepBuilderAPI_MakeFace(gp_Sphere(gp::XOY(), 6.0));
if (bSubdivision)
{
BRepMesh::Mesh(aFace, 1.0);
}
BRepTools::Dump(aFace, std::cout);
BRepTools::Write(aFace, dumpFile);
}
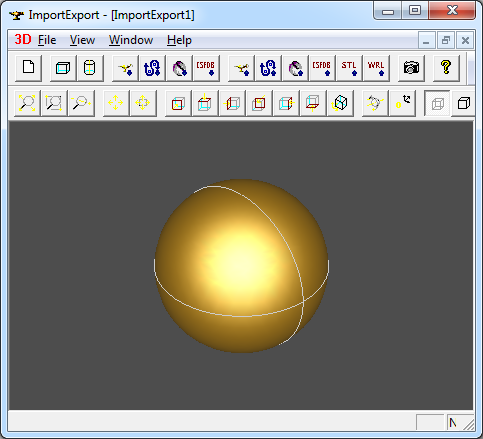
其中參數(shù)bSubdivision用來(lái)生成顯示用的網(wǎng)格數(shù)據(jù)，這里會(huì)生成Poly_Triangulation，將生成的BRep文件導(dǎo)入進(jìn)行顯示如下圖所示：
Figure 3.3.1 Import a Face from brep
四、示例程序 Example Code
將上述代碼放在一起，完整的程序代碼如下所示：
/*
* Copyright (c) 2013 eryar All Rights Reserved.
*
* File : Main.cpp
* Author : eryar@163.com
* Date : 2013-12-21 21:18
* Version : 1.0v
*
* Description : Use BRepTools to dump and write BRep files.
*
* Key Words : OpenCascade, BRep, Vertex, Edge, Face
*
*/
// OpenCascade library.
#define WNT
#include <gp_Pnt.hxx>
#include <gp_Circ.hxx>
#include <gp_Sphere.hxx>
#include <TopoDS_Vertex.hxx>
#include <TopoDS_Edge.hxx>
#include <TopoDS_Face.hxx>
#include <BRepMesh.hxx>
#include <BRepTools.hxx>
#include <BRepBuilderAPI_MakeVertex.hxx>
#include <BRepBuilderAPI_MakeEdge.hxx>
#include <BRepBuilderAPI_MakeFace.hxx>
#pragma comment(lib, "TKernel.lib")
#pragma comment(lib, "TKMath.lib")
#pragma comment(lib, "TKBRep.lib")
#pragma comment(lib, "TKMesh.lib")
#pragma comment(lib, "TKTopAlgo.lib")
void TestVertex(void)
{
ofstream dumpFile("vertex.brep");
TopoDS_Vertex aVertex = BRepBuilderAPI_MakeVertex(gp_Pnt(1.0, 2.0, 3.0));
BRepTools::Dump(aVertex, std::cout);
BRepTools::Write(aVertex, dumpFile);
}
void TestEdge(bool bSubdivision = false)
{
ofstream dumpFile("edge.brep");
TopoDS_Edge anEdge = BRepBuilderAPI_MakeEdge(gp_Circ(gp::XOY(), 6.0));
if (bSubdivision)
{
BRepMesh::Mesh(anEdge, 1.0);
}
BRepTools::Dump(anEdge, std::cout);
BRepTools::Write(anEdge, dumpFile);
}
void TestFace(bool bSubdivision = false)
{
ofstream dumpFile("face.brep");
TopoDS_Face aFace = BRepBuilderAPI_MakeFace(gp_Sphere(gp::XOY(), 6.0));
if (bSubdivision)
{
BRepMesh::Mesh(aFace, 1.0);
}
BRepTools::Dump(aFace, std::cout);
BRepTools::Write(aFace, dumpFile);
}
int main(void)
{
TestVertex();
TestEdge(true);
TestFace(true);
return 0;
}
也可以把更易懂的信息dump出來(lái)，這樣可以更好地理解brep文件的格式。當(dāng)將球面導(dǎo)出為brep文件時(shí)，會(huì)生成很多信息，如下所示：
Shape : 7, FORWARD
Dump of 7 TShapes
-----------------
Flags : Free, Modified, Checked, Orientable, Closed, Infinite, Convex
TShape # 1 : FACE 1101000 01807868
+2
NaturalRestriction
Tolerance : 1e-007
- Surface : 1
TShape # 2 : WIRE 0101100 01807CE8
-5 +4 +5 -3
TShape # 3 : EDGE 0101000 01808C10
+6 -6
Tolerance : 1e-007
same parametrisation of curves
same range on curves
degenerated
- PCurve : 4 on surface 1, range : 0 6.28319
UV Points : 0, 1.5708 6.28319, 1.5708
TShape # 4 : EDGE 0101000 01807AA0
+7 -7
Tolerance : 1e-007
same parametrisation of curves
same range on curves
degenerated
- PCurve : 3 on surface 1, range : 0 6.28319
UV Points : 0, -1.5708 6.28319, -1.5708
TShape # 5 : EDGE 0101000 018078C8
+7 -6
Tolerance : 1e-007
same parametrisation of curves
same range on curves
- Curve 3D : 1, range : -1.5708 1.5708
- PCurve : 1, 2 (C0) on surface 1, range : -1.5708 1.5708
UV Points : 6.28319, -1.5708 6.28319, 1.5708
UV Points : 0, -1.5708 0, 1.5708
TShape # 6 : VERTEX 0101101 018076F0
Tolerance : 1e-007
- Point 3D : 3.67394e-016, 0, 6
TShape # 7 : VERTEX 0101101 01807680
Tolerance : 1e-007
- Point 3D : 3.67394e-016, 0, -6
-------
Dump of 4 Curve2ds
-------
1 : Line
Origin :6.28319, 0
Axis :0, 1
2 : Line
Origin :0, 0
Axis :0, 1
3 : Line
Origin :0, -1.5708
Axis :1, 0
4 : Line
Origin :0, 1.5708
Axis :1, 0
-------
Dump of 1 Curves
-------
1 : Trimmed curve
Parameters : 4.71239 7.85398
Basis curve :
Circle
Center :0, 0, 0
Axis :0, -1, 0
XAxis :1, 0, 0
YAxis :-0, 0, 1
Radius :6
-------
Dump of 0 Polygon3Ds
-------
-------
Dump of 0 PolygonOnTriangulations
-------
-------
Dump of 1 surfaces
-------
1 : SphericalSurface
Center :0, 0, 0
Axis :0, 0, 1
XAxis :1, 0, -0
YAxis :-0, 1, 0
Radius :6
-------
Dump of 0 Triangulations
-------
-------
Dump of 0 Locations
-------
根據(jù)上面的數(shù)據(jù)，可以很好地理解BRep中拓樸形狀的相關(guān)數(shù)據(jù)。大部分?jǐn)?shù)據(jù)還是很直觀，便于理解的。其中有個(gè)數(shù)據(jù)可能需要解釋即PCurve（Parametric Curve），它是在參數(shù)（u,v）空間的曲面上的參數(shù)曲線。可能有些不好理解，結(jié)合程序代碼看下PCurve的使用，就會(huì)Aha!恍然大悟的：
//=================================================================//function : D0
//purpose :
//=================================================================
void BRep_CurveOnSurface::D0(const Standard_Real U, gp_Pnt& P) const
{
// shoud be D0 NYI
gp_Pnt2d P2d = myPCurve->Value(U);
P = mySurface->Value(P2d.X(),P2d.Y());
P.Transform(myLocation.Transformation());
}
此函數(shù)的作用是求PCurve上對(duì)應(yīng)參數(shù)u的曲面上的點(diǎn)，即0次微分D0。根據(jù)PCurve上的一個(gè)參數(shù)u，可以求出對(duì)應(yīng)參數(shù)u的PCurve上的點(diǎn)，把這個(gè)點(diǎn)的x,y分別作為參數(shù)曲面的參數(shù)u,v，即求出了曲面上的點(diǎn)。
五、結(jié)論 Conclusion
通過(guò)程序代碼將《BRep Format Description White Paper》中數(shù)據(jù)進(jìn)行讀寫(xiě)，深入理解OpenCascade的邊界表示法的數(shù)據(jù)結(jié)構(gòu)模塊ModelingData，為理解其他模塊打下基礎(chǔ)。
在邊界表示法中，理論上表示一個(gè)物理模型只需要三個(gè)拓樸體（頂點(diǎn)TopoDS_Vertex、邊TopoDS_Edge和面TopoDS_Face），所以在對(duì)brep文件輸出時(shí)，只處理了這三種拓樸體的信息。在生成形狀時(shí)，主要也是處理這三種拓樸體，再根據(jù)他們生成其他拓樸體。
頂點(diǎn)、邊和面的幾何之間的聯(lián)系在brep中也保存起來(lái)了，有了這些信息，就可以判斷一個(gè)頂點(diǎn)是不是邊上的點(diǎn)等。通過(guò)示例程序，來(lái)理解參數(shù)曲線PCurve。
理解了brep表示的結(jié)構(gòu)后，下一步準(zhǔn)備來(lái)研究下造型算法模塊ModelingAlgorithms。
六、參考資料 References
1. BRepTools_ShapeSet.cpp of OpenCascade
2. TopTools_ShapeSet.cpp of OpenCascade
3. BRepTools.cpp Of OpenCascade
4. BRep Format Description White Paper of OpenCascade
5. 孫家廣等. 計(jì)算機(jī)圖形學(xué). 清華大學(xué)出版社, 2000
6. 詹海生等, 基于ACIS的幾何造型技術(shù)與系統(tǒng)開(kāi)發(fā), 清華大學(xué)出版社, 2002