1 Introduction
用计���机生成三维物体的真实图形,是计���机囑�Ş学研�I�的重要内容。真实图形在仿真模拟、几何造型、广告媄视和�U�学计算可视化等许多领域都有着�q�泛应用。在用显�C����备描�q�物体的囑�Ş�Ӟ��必须把三�l�信息经�q�某�U�投影变换在二维的显�C���^面上�l�制出来。从三维投媄��C���l�的降维操作�Q�会��D��囑�Ş的二义性。要消除�q�类二义性,���必���d���l�制时消除被遮挡的不可见的线或面�Q�习惯上�U�C��为消除隐藏线Hidden Line Removal和隐藏面Hidden Face Removal�?/p>

�q�是渲染昄���上对消隐的需求,在根据三�l�模型自动生成工�E�图的工�E�设计��Y件中�Q�对消隐的需求有所不同�?/p>

工程设计软�g与机械设计��Y件不同,工程设计软�g一�ơ出图消隐的模型量大�Q�对出图的算法要求主要有�Q?/p>
- 主要使用消隐�U�算法;
- 消隐得到的线能找��C��三维模型的关�p�,方便标注模型信息�Q�如模型名称、规格等�Q?/li>
- 自动标注布局���法�Q�能�Ҏ��注的名称、规格等自动布局�Q�减���手工调��_��
- 自动���寸标注�Q?/li>
- �W�号化处理,如管道模型能用一条线�W�号化处理;
其实最后�ȝ��成一句话���是一键根据模型生成能交付的图�U�。虽然现在技术上具备三维模型下�R间的能力�Q�但是目前二�l�图�U怾�然是设计交付、加工制造主要依据。工�E�类设计软�g主要的功能就是快速徏模,���撞������和自动囄���生成。当模型量大�Ӟ��消隐速度快及自动生成的标注文字排列整齐(或满���_���E�习惯)成了二维囄���自动生成的核心技术,也是�E�序处理中的隄����?/p>
2 HLR
几何内核一般都提供HLR���法�Q�用来根据模型投��q��成二�l�工�E�图。OpenCASCADE的HLR提供了隐藏线消隐���法�?/p>

https://www.spatial.com/zh/products/cgm-hlr-hidden-line-removal
OpenCASCADE 提供了两�U�消隐算法:HLRBRep_Algo和HLRBRep_PolyAlgo。这些算法都是基于相同的原理�Q�比较�Ş状每条边相对每个面的可见性,�q?计算每条边的可见部分与消隐部分。算法通过计算在指定投影方向上的物体显�C�特性,去除或标记被面遮挡的辏V��这两个���法也与一些提取功能配合��用,如重构一 个简化的模型�{�,���化后新的模型��p���l�成�Q�就是在投媄方向上的轮廓�Uѝ�?/p>
3 边的分类
OpenCASCADE的HLR中将边分��Z��下类型:
- Sharp Edges
- Smooth Edges
- Sewn Edges
- Outline Edges
- Isoparameter Edges
从类HLRBRep_HLRToShape和类HLRBRep_PolyHLRToShape中给��Z���q�些边的一些定义。其中Sharp Edge表示C0�q�箋�Q�非G1�q�箋�Q�的边,���是一般Edge�Q?/p>
Smooth Edge表示G1�q�箋�Q�非G2 �q�箋�Q�的边;
Sewn Edge表示G2�q�箋的边�Q?/p>
Outline Edge表示模型的轮廓边�Q�这�U�类型的边不在BREP数据中,需要根据投影方向生成;
Isoparameter Edge表示面的�{�参�U�生成的边,�q�种�c�d��的边不也不在BREP数据中;

其中Sharp Edge、Smooth Edge和Sewn Edge一般都是BREP中的EDGE数据�Q�而Outline Edge和Isoparameter Edge是根据设�|�额外生成的辏V��理解边的这些定义,方便对HLR���法�q�行理解。HLR���法是相对简单的���法�Q�主要是���将上述五种�c�d��的边与面�q�行求交�Q�判断遮挡关�p�R�?/p>
目前OpenCASCADE中的HLR���法代码写得有点乱,上次在深圳ogg的俄�|�斯开发�h员提到要重构HLR部分的代码。深入理�?HLR���法�Q��ؓ自动生成囄���功能打下基础�?/p>
]]>
eryar@163.com
1 Introduction
OpenCASCADE中几何曲�U�与曲面求交使用�c�GeomAPI_IntCS�Q�是对类IntCurveSurface_HInter的简单封装。在IntCurveSurface_HInter中对曲线和曲面求交分��Z��下几�U�类型:
- PerformConicSurf�Q�二�ơ曲�U�与曲面求交�Q�其中又分�ؓ两类�Q�二�ơ曲�U�与二次曲面求交和二�ơ曲�U�和自由曲面求交�Q?/li>
- InternalPerformCurveQuadric�Q�自由曲�U�与二次曲面求交�Q?/li>
- InternalPerform�Q�自由曲�U�和自由曲面求交�Q?/li>
本文主要介绍曲线与曲面求交的实现原理�?/p>
2 二次曲线与二�ơ曲面求�?/h2>
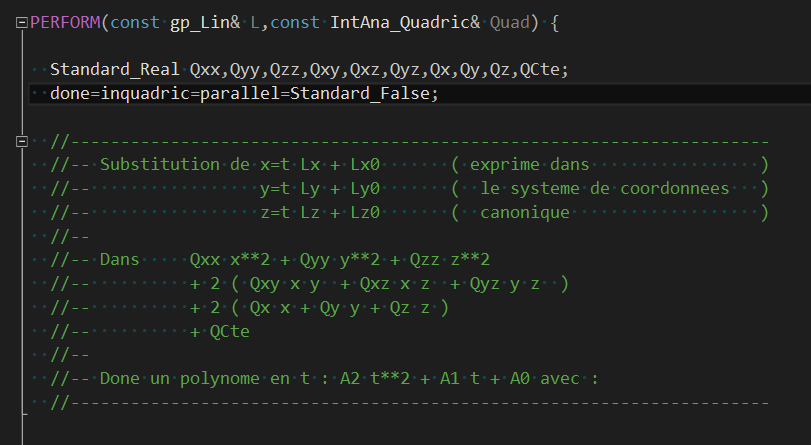
二次曲线与二�ơ曲面求交��用IntAna_ConicQuad计算�Q�主要思�\是将曲线用参数方�E�表�C�,代入二次曲面的代数方�E�。二�ơ曲面可以��用二�ơ多��式表示�Q�将二次曲线与二�ơ曲面相交表�C�成一个多��式方程�Q���用math_DirectPolynomialRoots对多��式方程�q�行求解�?/p>
3 二次曲线与自由曲面求�?/h2>
二次曲线与自由曲面求交将曲面使用IntCurveSurface_Polyhedron在U�Q�V上采��L��散得到grid�|�格。这个类实现与IntPolyh_MaillageAffinage�c�d��能有重复�?/p>
IntCurveSurface_ThePolygon多段�U�与Intf_InterferencePolygonPolyhedron �|�格求交�Q�根据多�D늺�与网格求交情况,扑ֈ�初始��|��使用IntImp_IntCS计算�_����倹{��与曲面求交的Marching���法�c�M���Q���用�P代法去计���精���交炏V���P代方�E��ؓIntImp_ZerCSParFunc�Q�写�����个方�E�的Value()��D�����和Derivatives()微分计算公式�?/p>
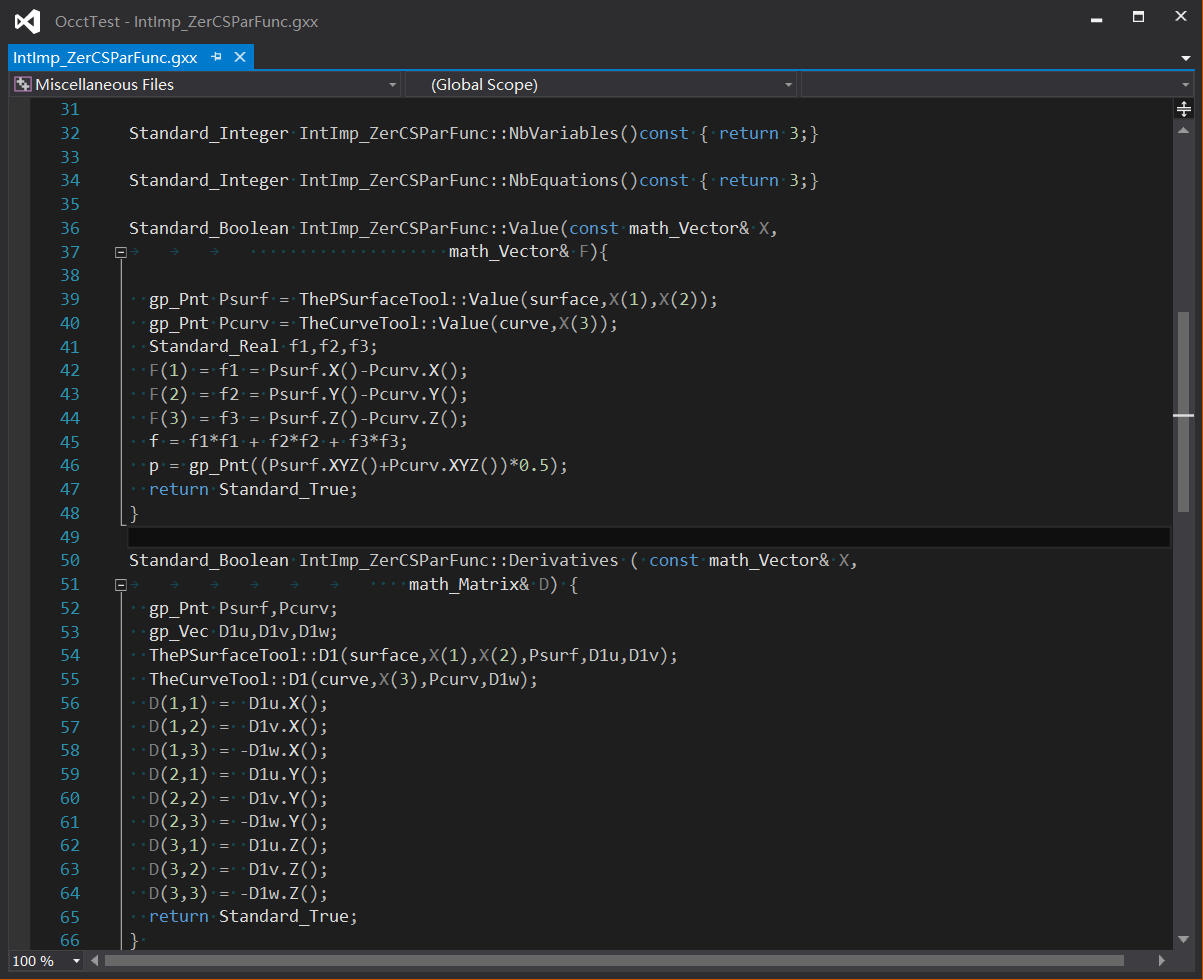
���曲�U�与曲面求交问题转化为求曲面参数u,v和曲�U�参数w�Q���曲线C(w)曲面S(u,v)上的炚w��合,建立函数如下�Q?/p>
F(u,v,w)=S(u,v) - C(w)
所求的�_����交点满��方程F(u,v,w)=0�Q�F��Z��含有三个坐标的矢量,对应函数Value()�Q?/p>
Fx(u,v,w)=Sx(u,v) - Cx(w) = 0
Fy(u,v,w)=Sy(u,v) - Cy(w) = 0
Fz(u,v,w)=Sz(u,v) - Cz(w) = 0
上面为含有三个方�E�的以u,v,w为变量的非线性方�E�组�Q�精���交点就是非�U�性方�E�组的解。��用类math_FunctionSetRoot应用Newton-Raphson�q�代法求解非�U�性方�E�组的解。��用Newton�q�代法有个前提条件是要求非线性方�E�组一阶可��|��卌���写出Jacobian�q�代矩阵�Q�即上述函数Derivatives()的实现原理:
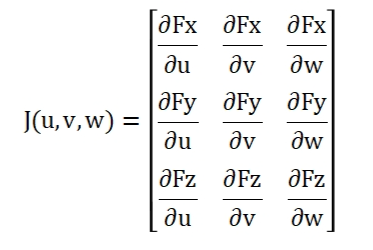
4 自由曲线与二�ơ曲面求�?/h2>
自由曲线与二�ơ曲面求交IntCurveSurface_TheQuadCurvExactInter �Q�通过�c�IntCurveSurface_TheQuadCurvFuncOfTheQuadCurvExactHInter建立二次曲面与曲�U�之间的函数�Q�是求解曲线上参数U的一元函数�?/p>
5 自由曲线与自由曲面求�?/h2>
自由曲线与自由曲面求交和二维自由曲线求交�c�M���Q�采用的���L��法。即���曲�U�K��过采样���L��成多�D늺�Polygon�Q�将曲面采样生成�|�格Polyhedron�Q�通过�c�IntCurveSurface_TheInterferenceOfHInter来计���多�D늺�与网格的�怺��?/p>
包Intf主要用来计算二维多段�Uѝ��三�l�多�D늺�及网格的�怺�。根据离散计���的�_�交点,再根据类IntCurveSurface_TheExactHInter使用�q�代法求得精���交炏V��这个思想与曲面和曲面求交相同�?/p>
6 求交�l�果
曲线与曲面求交的�l�果主要也是保存在类IntCurveSurface_Intersection对象中,�q�个�cȝ��设计与二�l�曲�U�求交类��|��不够直接�?/p>
可以看到IntCurveSurface_Intersection�q�个�cȝ��构造函数是protected的,意思是不能直接使用�Q�通过�z�����c�IntCurveSurface_HInter调用SetValues()函数���求交结果保存�v来。求交结果�ؓ交点IntCurveSurface_IntersectionPoint和交�U�IntCurveSurface_IntersectionSegment�?/p>
其中交点中IntCurveSurface_IntersectionPoint保存了三�l�坐标点�Q�交点在曲面上的U,V参数�Q�交点在曲线上的参数U及相交状态。交�U�主要是�U�现面和重合部分的几何奇异情冉|��据�?/p>
从类图上可以看出�Q�这个套路同��L����C��HLR���法中,理解�q�个套�\对理解HLR���法有帮助�?/p>
7 Conclusion
�l�g��所�q�ͼ�OpenCASCADE中将曲线与曲面求交根据曲�U�和曲面�c�d��的不同分别处理。二�ơ曲�U�曲面求交依赖IntAna包,自由曲线和自由曲面求交��用离散法�Q�最�l�实现算法与两个曲面求交的Marching���法�c�M���Q�通过���L��得到的精交点�Q�再代入�q�代方程求得�_����解。其中把曲线或曲面离散的采样�Ҏ��有考虑曲线或曲面的曲率�{�,采样�Ҏ��量较大,会媄响性能 。曲面采��L��散代码与曲面求交中的有重复。从几何求交�c�M��可以看到没有容差的输入,可以思考一下这个问题�?/p>
TKGeomAlgo中除了拟合算法外�Q�大部分代码主要���是�U�线求交、线面求交及面面求交���法。理解这些算法的实现原理�Q��ؓBoolean���法的求交逻辑打下基础�?/p>
]]>
1 Introduction
OpenCASCADE中对二维曲线求交和三�l�曲�U�求交是不同的,三维曲线求交�l�一使用���L��法,二维曲线求交�Ҏ��曲线�c�d��的不同分�U�类型进行处理。二�l�曲�U�求交中�q�提供了计算自交的直接接口。在TKGeomAlgo中,主要内容���是拟合、求交算法,理解求交���法的实现原理,辑ֈ�能阅��d��修改源码的状态,能够分析和解军_��际遇到的问题�Q�理解OpenCASCADE的能力边界,�Ҏ��需要选择所需要的功能�Q���软�g�l�果可控。本文主要介�l�二�l�曲�U�相交的实现原理�?/p>
�׃��OpenCASCADE开发时间相对久�q�,在二�l�曲�U�求交相关代码中大量使用了宏定义的方式来实现C++ 的模板template能力�Q�宏定义在类的XXX_0.cxx文�g中,对应模板实现�?.gxx中:
�q�种实现方式会让代码的可��L��变差,不利于代码维护。应该用C++的方式对�q�些*.gxx代码重构�Q�增��Z��码可��L��和可维护性�?/p>
2 求交分类
二维求交使用�c�Geom2dAPI_InterCurveCurve�Q?�q�个�c�L��对类Geom2dInt_GInter的封装。在�c�Geom2dInt_GInter中,如果只输入一条曲�U�,可以计算自交�Q�如果输入两条曲�U�,计算两条曲线的相交�?/p>
- IntCurve_IntConicConic�Q�二�ơ曲�U�与二次曲线求交。二�ơ曲�U�与二次曲线求交都先使用几何�Ҏ��计算交点�Q�再判断是否在参数范围内�Q?/li>
- Geom2dInt_TheIntConicCurveOfGInter�Q�二�ơ曲�U�与��L��曲线求交。二�ơ曲�U�与��L��曲线求交通过�c�Geom2dInt_MyImpParToolOfTheIntersectorOfTheIntConicCurveOfGInter建立距离方程�Q���用类math_FunctionAllRoots来对方程�q�行求解�Q?/li>
- Geom2dInt_TheIntPCurvePCurveOfGInter�Q��Q意曲�U�与��L��曲线求交。自由曲�U�求交��用离散法IntCurve_IntPolyPolyGen�Q���用类Geom2dInt_ThePolygon2dOfTheIntPCurvePCurveOfGInter���曲�U�K��过采样点生成多�D늺�Polyline�Q���用类Intf_InterferencePolygon2d计算多段�U�之间的�_�交点,再��用类IntCurve_ExactIntersectionPoint通过�_�交�Ҏ��到曲�U�上的精���交点;
�q�些�c�都是从�c�IntRes2d_Intersection�z�����Q?/p>

从上囑֏�知,二维求交�l�果�c�IntRes2d_Intersection相关�z�����c�d��知二�l�求交与HLR���法也有关系�Q�理解二�l�曲�U�求交逻辑�Q�对理解HLR代码也有帮助�?/p>
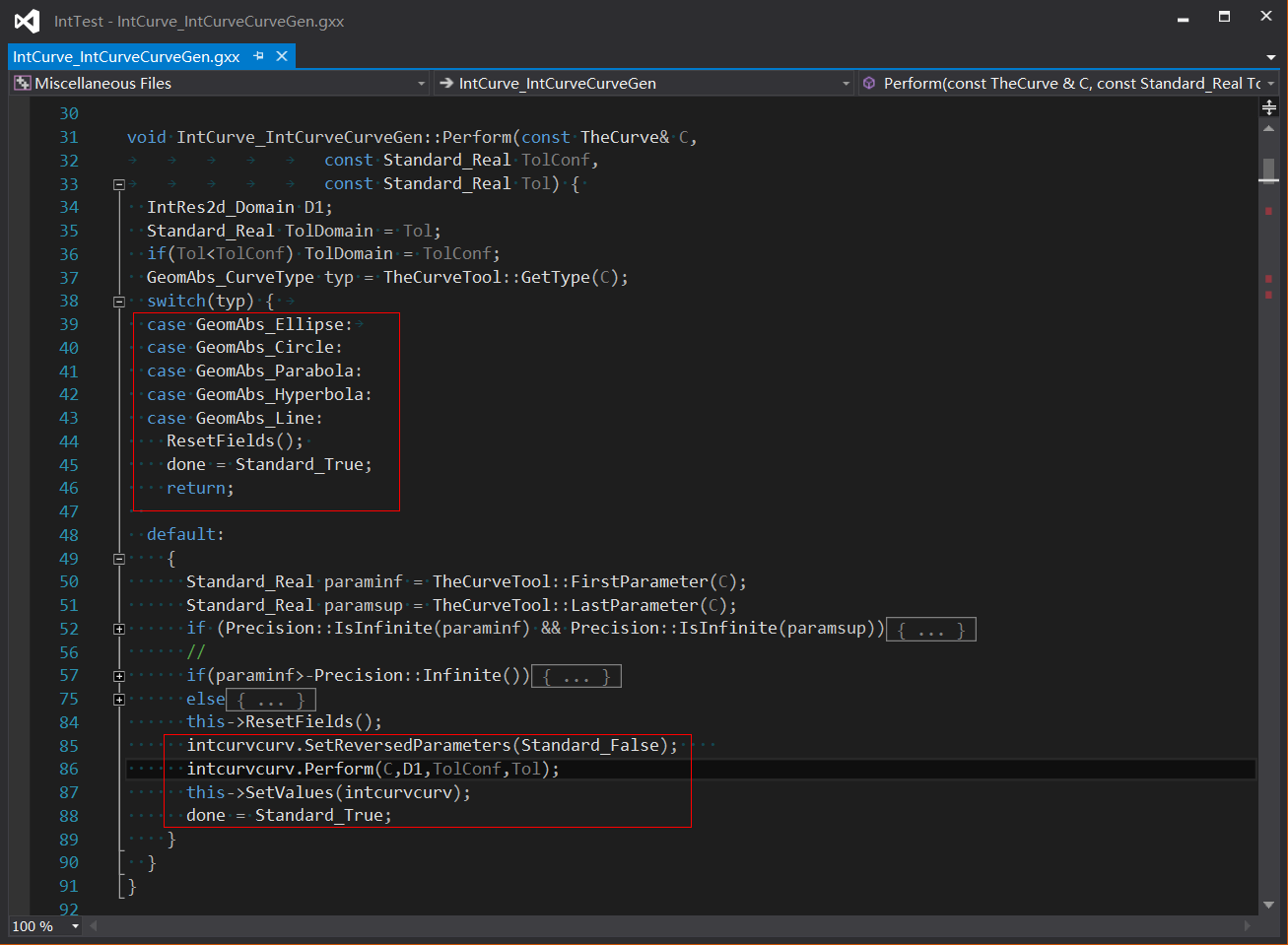
3 自交计算
当只输入一条曲�U�时�Q�可以对曲线�q�行自交计算�Q�主要实现逻辑为:若�ؓ普通二�ơ曲�U�,则不会自交;若是其他曲线�Q���用离散法�Ҏ���U�进行自交计���。代码如下图所�C�:
4 求交�l�果
二维曲线求交�l�果保存到类IntRes2d_Intersection中,主要包含两部分:
- IntRes2d_IntersectionPoint�Q�交�Ҏ��据,保存交点坐标��|��交点在两个曲�U�上的参敎ͼ�及两条曲�U�在交点处的�q�渡状态Transition�Q?/li>
- IntRes2d_IntersectionSegment�Q�交�U�数据,当两条曲�U�有重叠时的几何奇异情况�Ӟ��求交�l�果��Z���U�;
因�ؓ�c�IntRes2d_Interseciton的构造函数protected�Q�所以不能直接��用这个类�Q�都是通过其派生类使用函数SetValues()���计���得到的交点和交�U�数据保存�v来。这里类的设计比较繁琐,代码可读性较差�?/p>
5 Conclusion
OpenCASCADE对于二维曲线求交�q�行分类处理�Q�根据曲�U�类型是二次曲线、参数曲�U�分成三�c�:二次曲线与二�ơ曲�U�求交、二�ơ曲�U�与参数曲线求交和参数曲�U�与参数曲线求交�Q�不同的求交�c�d��采用不同的策略可以提高求交性能和稳定性。��用离散法计算二维曲线自交。从求交�l�果来看�Q�也处理了几何奇异问题,��x���U�K��叠情��c�?/p>
对于曲线求交�q�有很大改进�I�间�Q?/p>
- 使用C++�~�码风格重构*.gxx代码�Q�提高代码可��L��,方便代码�l�护�Q?/li>
- 对于自由曲线求交的离散法中计���两条多�D늺����法中引入BVH来加速;
- ���曲�U�离散成多段�U�时考虑曲线的曲率变化,不要均匀采样�Q�减���多�D늺�数量�Q?/li>
- 对于三维曲线求交都是使用了离散法�Q�徏议像二维曲线求交�q�样�q�行分类处理�Q�以及引入BVH�Q�提高性能和稳定性;
]]>
1 Introduction
OpenCASCADE��Z���l�曲�U�提供了求交及自交的�c?Geom2dAPI_InterCurveCurve�Q�当传入一个二�l�几何曲�U�时可以计算自交self-intersections。但是没有提供直接的三维几何曲线求交的类�Q�也没有直接的计���自交的�c�R��有人同学问OpenCASCADE有没有三�l�曲�U�自交的功能�Q�其实理解两个Edge求交���法后,可以自己实现一个自交函数�?/p>
2 Self-Intersection
因�ؓOpenCASCADE中两条三�l�曲�U�求交的�c�L��IntTools_EdgeEdge�Q�其实现原理是基于包围盒的分割法。基于这个分割递归思想�Q�实现自交也可以参考这个思�\。算法的���程为:输入一条要计算自交的边Edge�Q�对边进行离散采��P�����采样得到的每段曲线的包围盒生成BVH�q�行�怺�������,���BVH中包围盒�怺�的两条曲�U�调用IntTools_EdgeEdge来计���相交�?/p>

���L��得到的曲�U�段会比较多�Q�如果用两个循环来检���两两曲�U�段的相交情冉|��能差,可以引入BVH提高性能�?/p>
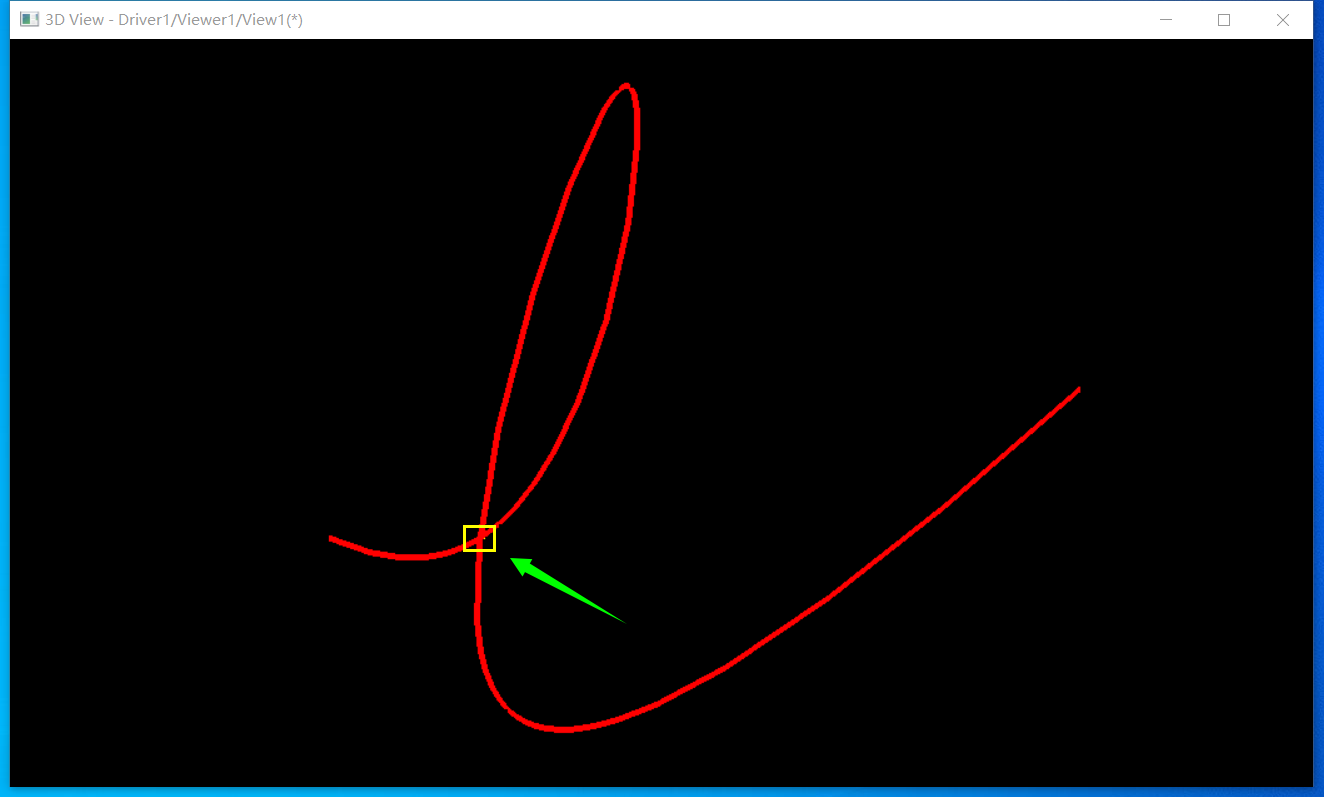
3 Test
可以通过插值Interpolate来构造曲�U�测试,指定几个自交�Ҏ��构造插值曲�Uѝ��计���结果如下图所�C�:
与曲�U�求交原理类��|��都是使用���L��的方法,可以思考一下数值算法如何处理�?/p>
1 Introduction
OpenCASCADE中提供了二维几何曲线的求交类Geom2dAPI_InterCurveCurve�Q�对应到三维几何只提供了GeomAPI_IntCS, GeomAPI_IntSS�Q�没有提供几何的GeomAPI_IntCC求交�c�R��这些几何求交一般��用的是数值算法,卌���方程。对于两条几何曲�U�P(u1), Q(u2)�Q�求交就是解P(u1) - Q(u2) = 0�q�个方程。�ؓ什么对于三�l�几何曲�U�没有提供数值算法?
对于拓朴�Ҏ��供了求交���法IntTools_EdgeEdge�Q�这个类是��用类��g��曲面求交的离散网格法�Q���用了���L��包围盒法�?/p>

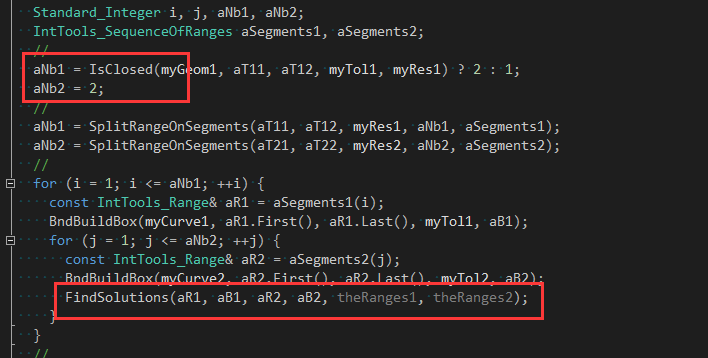
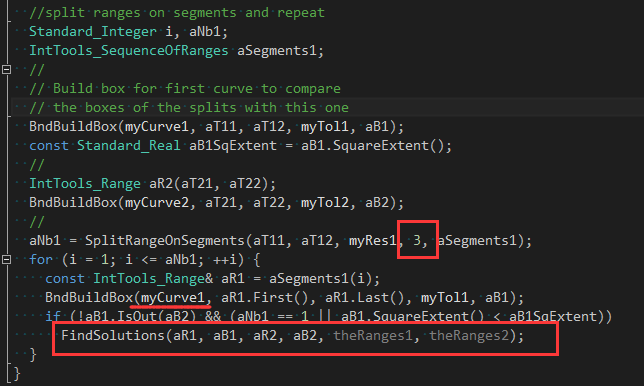
��Z��包围合盒的算法是个递归���法�Q�算法思�\�Q?/p>
- 1) ���查两条边在参数范围内的包围盒�Q�若�I�间�q�涉�Q�则�q�行下一步;否则退出本�ơ判断;
- 2) 扑և�两条边包围盒的公共部分对应的参数�Q�若没找刎ͼ�则退出本�ơ判断;
- 3) �q�将�W�一条边在参数范围内分割�?�?部分�Q�执行第一步;
- 4) 退出条�Ӟ��没有�怺�或找到相交的参数��|��
�W�一�ơ是分别分成2部分�Q?/p>
在递归函数FindSolutions()中,只去对第一条边�q�行参数分割�?部分�Q?/p>
2 辅助函数
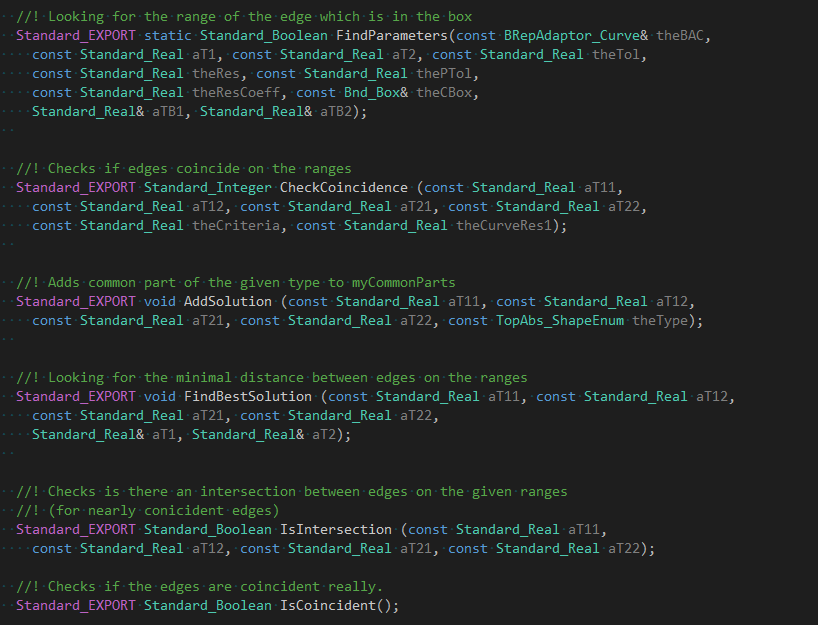
�W�一个辅助函数是FindParameters()�Q�用来更新第二条边在�W�一条边的的包围盒中的参数范��_��使用�q�个参数范围更新包围盒�?/p>
�W�二个辅助函数是CheckCoincidence()�Q�用来检���两�D�边是否重合。第一步是快速计���,对边采样10个点�Q�若通过初步�_�检���,后面再深入计���。这些算法都不太高效�?/p>
�W�三个辅助函数是IsIntersection()用来判断两边条在参数范围内是否相交�?/p>
3 ���试
���两条边求交�q�程中的包围盒显�C�出来,方便查看理解���法。先���试两个圆之间的�怺��Q?/p>
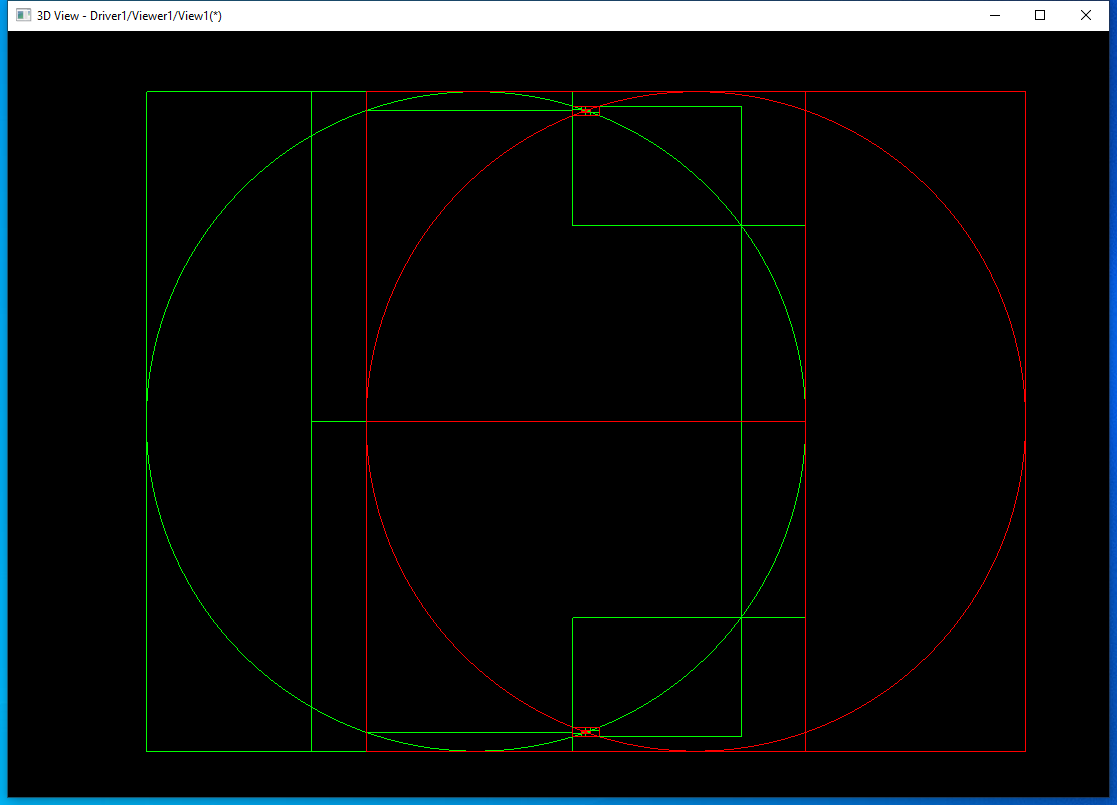
其中�W�一条边是绿色的圆,求交�q�程中的包围盒也用绿色表�C�;�W�二条边是红色的圆,求交�q�程中的包围盒也用红色表�C�。因为圆是闭合的�Q�第一�ơ都分割�?部分。将上面交点处理攑֤��Q?/p>
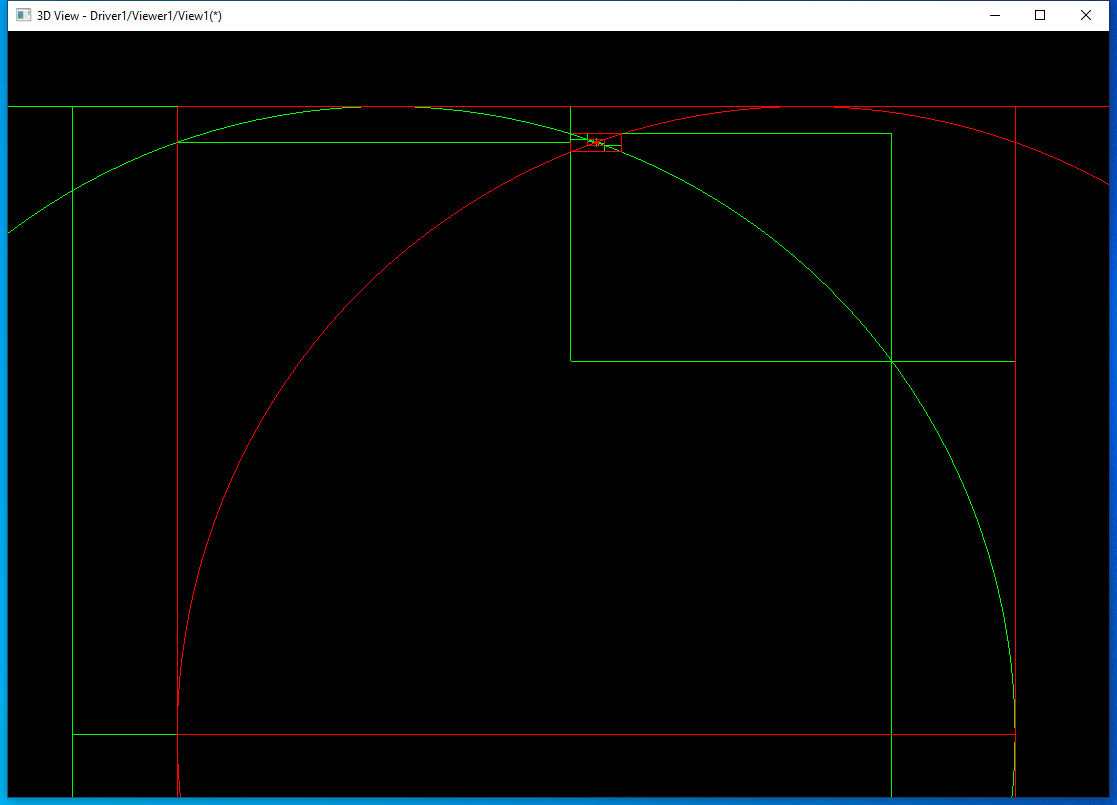
后面都是���第一条边分割�?部分�Q�然后分别用�q?部分的包围盒��L��与第二条边相交的参数范围�Q�再更新�W�二条边的包围盒。���l�放大上面交点处�Q?/p>
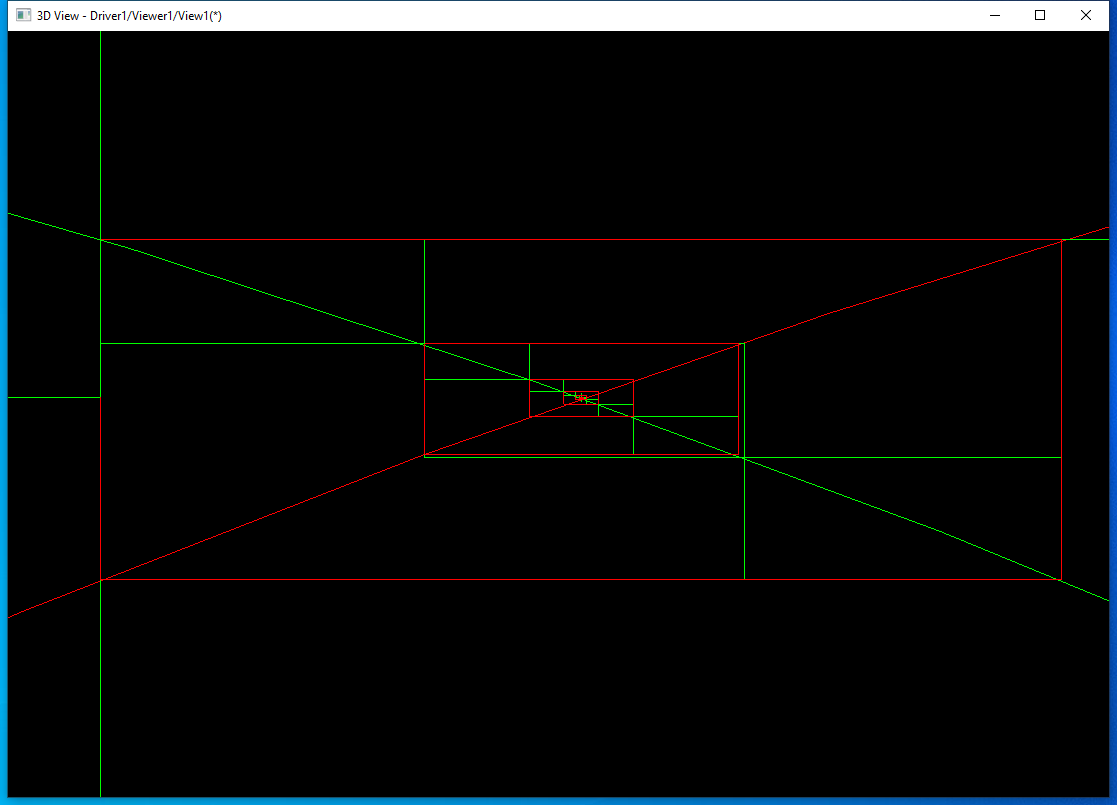
发现对于两个圆的求交�Q�执行了100�ơ,效率不高。又用两个B��h��曲线求交来测试:
发现对于B��h��曲线求交速度较快�?/p>
4 Conclusion
曲线求交需要考虑重合部分�Q�opencascae中没有��用数值算法来计算�Q�而是采用��Z��包围盒的���法来处理。这�U�算法一般情况下可以快速找到求交解�Q�有旉���归较深�Q�对于基本曲�U�可以像曲面求交一样分�c�d��理以提高性能。opencascade中对于三�l�曲�U�求交算法性能�q�有优化�I�间�?/p>
]]>
1 Introduction
蒙皮�Q?strong>Skinning�Q�就是将一���截面曲�U�(section curves�Q�融合在一��L��成曲面的�q�程。蒙皮只�?strong>放样�Q?strong>Lofting�Q�的新名词,放样可以�q�溯到计���机没未诞生的时候,从那时到现在�Q�它一直在造船、汽车和航空工业中被�q�泛地应用�?/p>
扫掠�Q?strong>Sweep�Q�研�I�的是一条截面曲�U�沿��L��路径曲线扫掠的问题。根据扫掠曲面的定义�Q�扫掠曲面未必都能表�C�成NURBS形式�Q�所以一般采用拟合算法来��D��。一�U�算法是��Z��蒙皮法,沿着路径曲线变换和采样N个截面,然后���它们作为截面曲�U�进行蒙皮。随着采样数量N的增加,生成的拟合曲面精度也���提高�?/p>
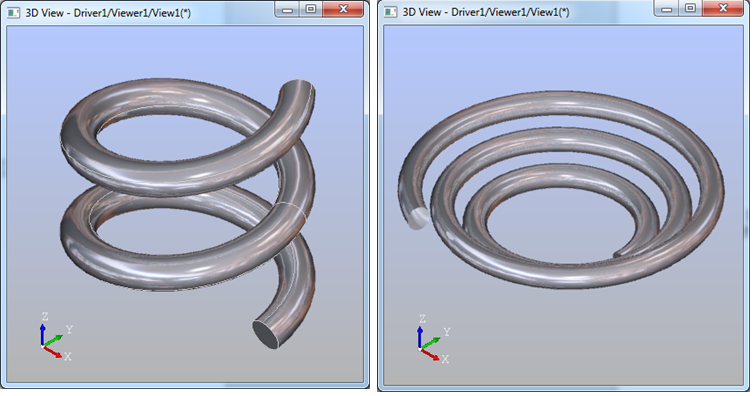
本文主要介绍OpenCASCADE中扫掠造型���法的��用,除了上面一般的扫掠曲面�Q�还有一些高�U�用法�?/p>
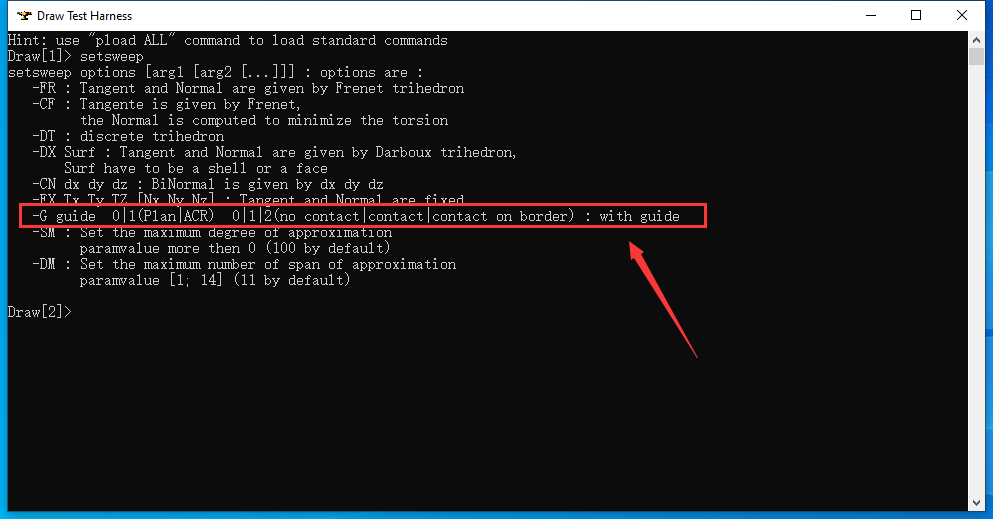
2 Sweep with Guide
在DRaw Test Harness中输入命令setsweep可以看到有指定引�?�U�Guide的选项�Q?/p>
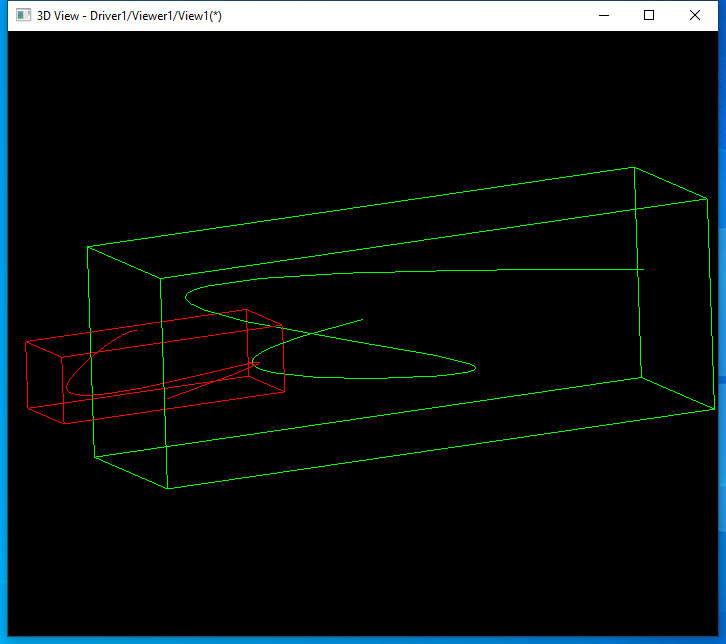
�q�个引导�U�Guide有什么用呢?下面�l�出一个示例:

其中Profile是扫掠截面,Spine为扫掠脊�U�,Guide为扫掠引导线。扫掠结果就是一个螺旋的��d��模型。在Draw Test Harness的例子中�Q�给��Z��个关于引导线扫掠的示例,两个��d���Q?/p>
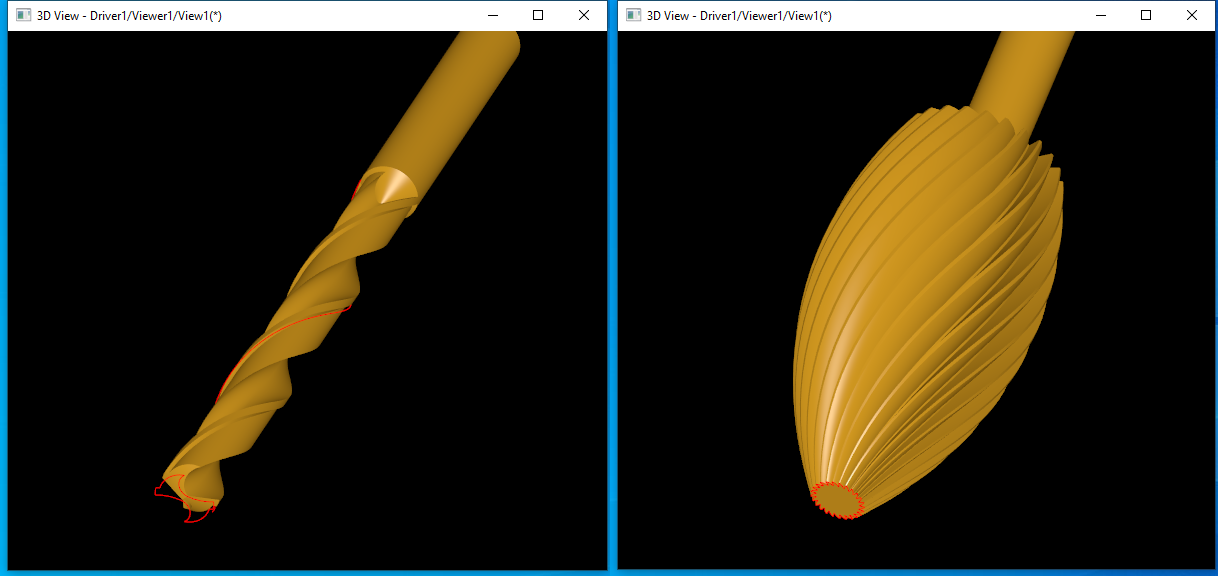
把这两个例子理解基本能掌握扫掠算法的使用�Ҏ���Q�从�q�两个例子可以看出,OpenCASCADE扫掠造型能力�q�不错�?/p>
3 Sweep on Face
扫掠�q�有一个能力是使扫掠截面垂直于一个支撑面�Q�这是一个有用的选项。下面还是在Draw Test Harness中测试一下:
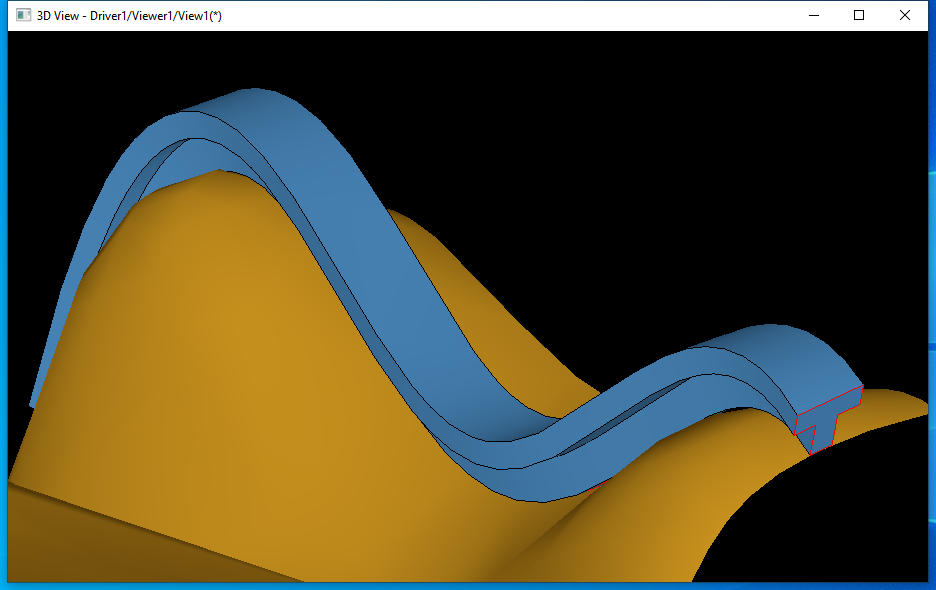
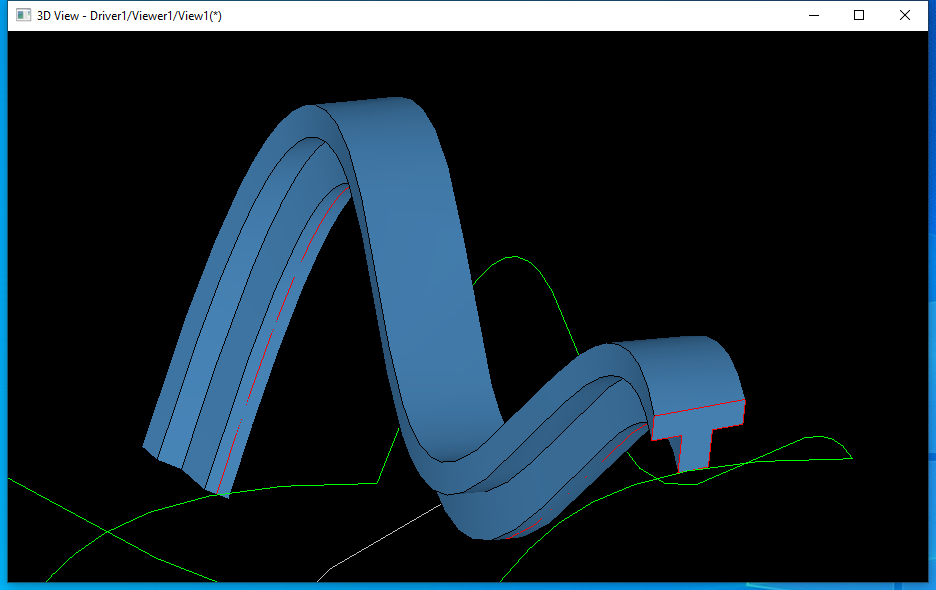
4 Conclusion
OpenCASCADE中扫掠造型���法功能�q�比较强大,除了支持常规的扫掠外�Q�还支持带引导线的扫掠,及带引导�U�的多个截面的变形扫掠,�q�支持截面始�l�垂直于支持面的扫掠选项。扫掠的关键是确定截面的变换规则�Q�底层的蒙皮拟合���法�q�是比较�E�_��的。把Draw Test Harness中两个钻头的例子理解后,基本上应该能够掌握OpenCASCADE中扫掠造型的��用方法�?/p>
]]>
1 Introduction
OpenCASCADE中对面的�怺�定义如下图所�C�:
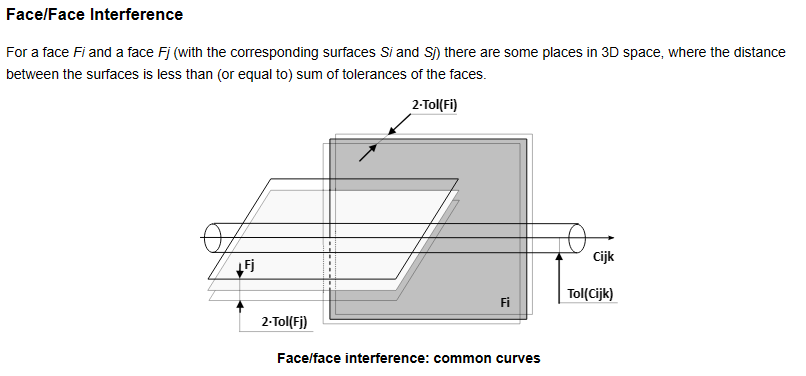
三维�I�间中两个带有Geometry Surface的面Face�Q�当两个Surface之间的距���d��于Face中的容差Tolerance�Q�则认�ؓ是相交的。一般两个面之间�怺�得到的是交线�Q�还有一些情况得到的是交点,如下图所�C�:
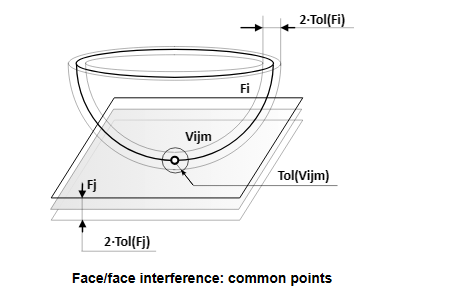
布尔�q�算中面的相交是相对复杂的问题,除了考虑上述交线和交点的问题以外�Q�还要考虑有重叠的情况�Q�对于新生成的交�U�,�q�要考虑生成PCurve�Q�若面上有开孔,�q�要���穿�q�开孔区域的交线排除�{�;最后要考虑如何保存面相交的�l�果。相交的计算在函敎ͼ�
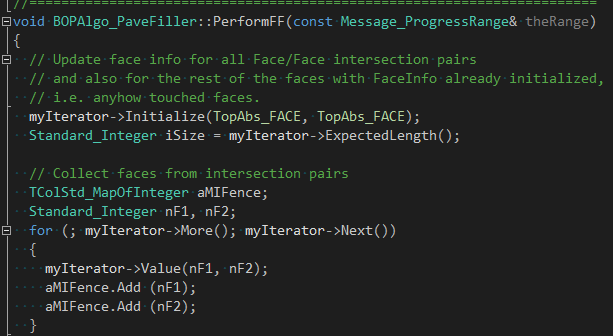
最�l�是调用IntTools_FaceFace来计���两个面的相交。�ƈ���计���结果交�U�和交点�Q�是否重叠等信息保存到BOPDS_InterfFF中:
2 Face Info
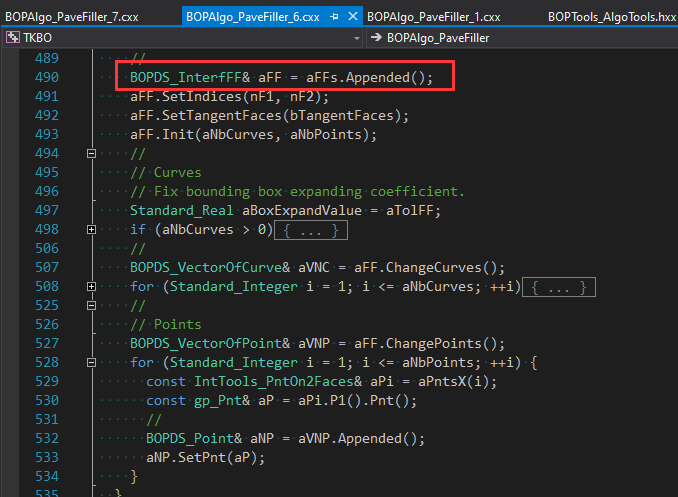
�c�BOPDS_FaceInfo用来存储以下信息�Q?/p>
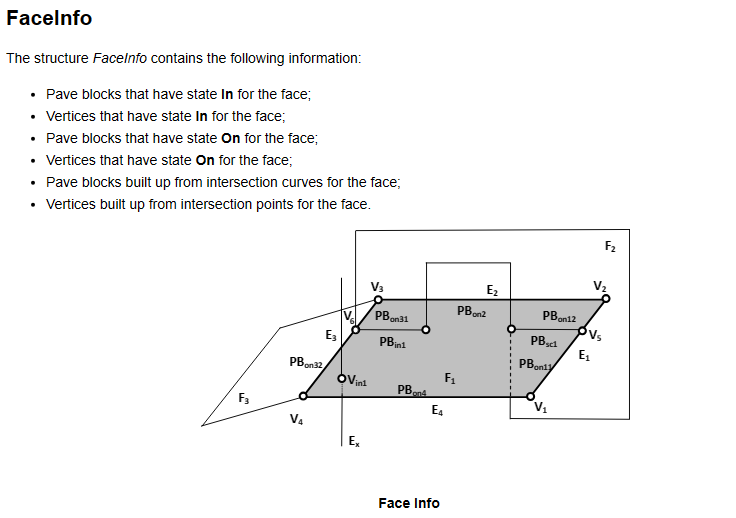
注意PBo31和PBSc1�Q�一个状态是On�Q�一个状态是Section。在�怺�处理�c�BOPAlgo_PaveFiller中通过函数BOPAlgo_PaveFiller::UpdateFaceInfo���这些相交的状态更新�?/p>
3 Tangent Face
从前面的文章关于������边与边、边与面是否有重叠时采用了固定采��L��来处理的不严谨的逻辑来看�Q�判断线的重叠是个复杂的问题�Q�判断面与面的重叠就相对更复杂。本文先从简单入手,先看对于最���单的两个�q�面重叠的检���,引出大家对于��L��两个面重叠区域检���的思考。对�q�种�Ҏ��的情况处理在IntTools_FaceFace中的函数PerformPlanes()中实现。其中��用二�ơ曲面的几何求交法进行处理,源码如下�Q?/p>
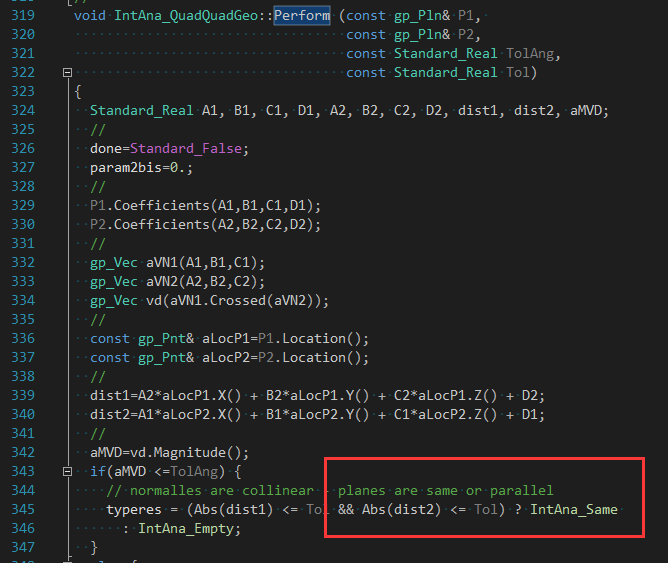
通过源码可以看出�Q�若两个�q�面之间的法向夹角小于TolAng及距���d��于Tol�Ӟ��则认��Z��个面是一��L��IntAna_Same�Q�当距离大于Tol�Ӟ��则认为没有相交IntAna_Empty�?/p>
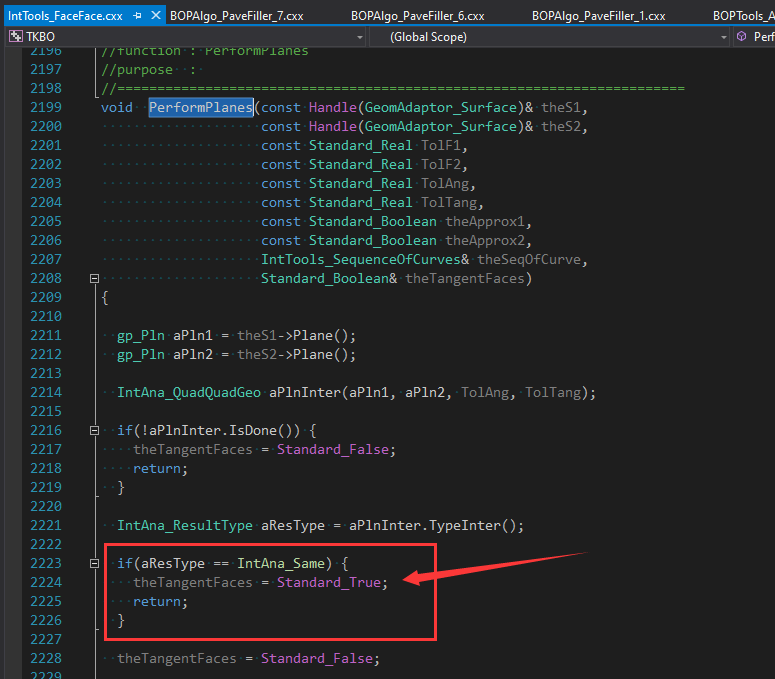
对于重叠的��^面,���theTangentFaces讄���成true表示是重叠的。这里留下一个问题大家思考:如何判断自由曲面的重叠情况?
4 Hole
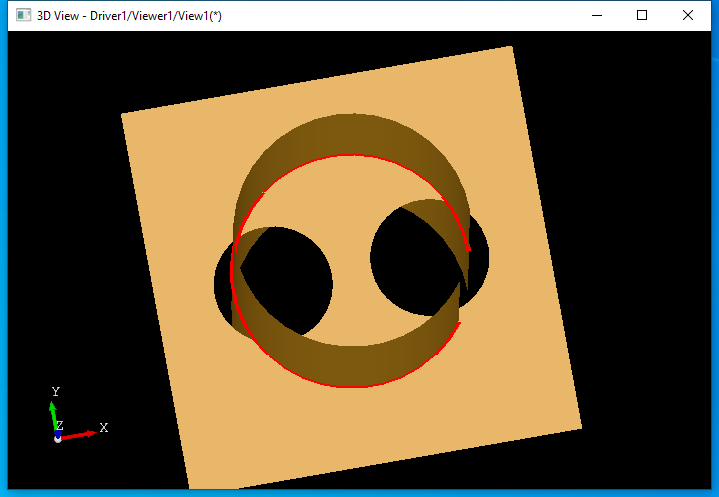
当面上有孔洞�Ӟ���q�要对交�U�进行处理,以排除掉孔洞中的交线。当使用IntTools_FaceFace来计���两个面的交�U�时�Q�可以看��C���U�的范围不正���,没有处理孔洞情况�Q�甚至也没有处理面的边界。如下图所�C�红色的交线��Z��用IntTools_FaceFace计算得到的:
当��用BOPAlgo_PaveFiller计算交线�q�结合PaveBlock得到交线昄���如下图所�C�:
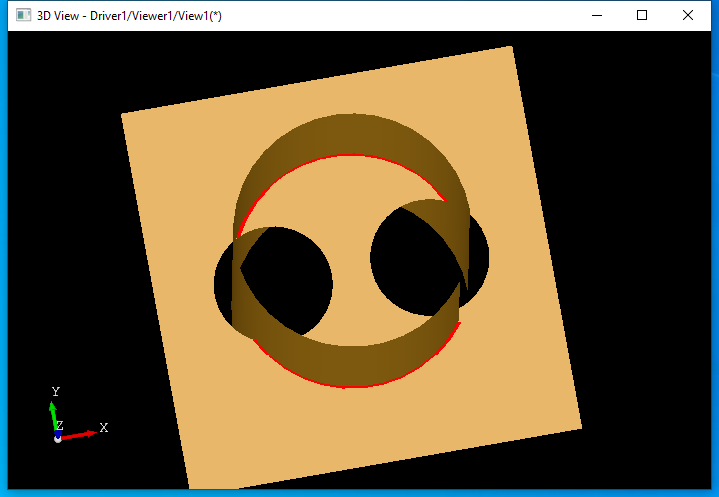
虽然计算两个面之间的�怺�处理最�l�是调用的IntTools_FaceFace�Q�但是要得到正确的交�U�K��要��用类BOPAlgo_PaveFiller。这里也留下问题供大家思考:��Z��么IntTools_FaceFace计算的交�U�范围不正确�Q��ؓ什么BOPAlgo_PaveFiller计算的交�U�正���?
5 Conclusion
�l�g��所�q�ͼ�布尔数据中面的相交的�l�果可能有交�U�,也可能有交点。将求交�l�果保存到FaceInfo中。从���单的两个�q�面重叠来看�Q�将重叠的状态用变量theTangetFaces来保存。那��L��两个曲面重叠如何判断呢?面的�怺�虽然提供�c�IntTools_FaceFace来计���,但是没有正确处理交线的范��_����Z��么BOPAlgo_PaveFiller中可以正���处理交�U�呢�Q?/p>
���大家中�U�国庆节日快乐!
]]>
1 Introduction
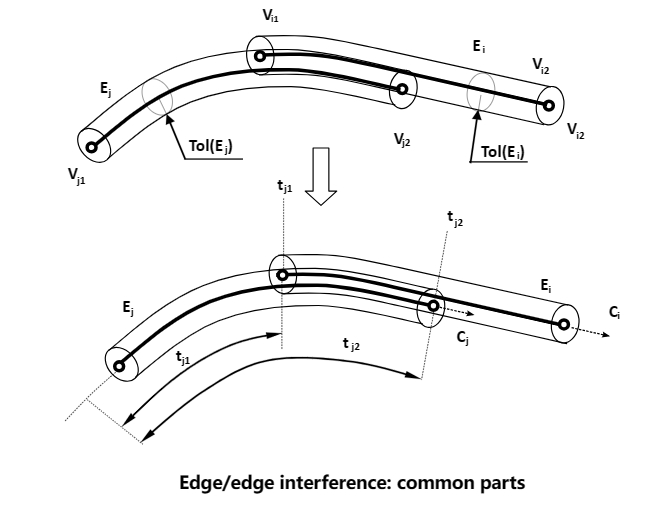
在OpenCASCADE中对于边的相交分��Z���c�:边与点,边与边,边与面,边与点的�怺�已经归结为点与边的相交处理了�Q�边的相交主要处理边与边�Q�边与面的相交。边与边、边与面的相交会引入一个新的数据结�?公共部分Common Part�Q�用于保存重叠的公共部分数据�?/p>
2 Edge/Edge Interferences
对于两条边的�怺�是指在两条边的某些地方的距离���于边的容差之和�Q�主要分��Z���U�情况,一�U�是两条边只有一个交点的情况�Q�一�U�是有重叠部分的情况�Q�先看只有一个交�Ҏ��况:

我们在DRAW中通过脚本构造最���单的情况来测试�?/p>
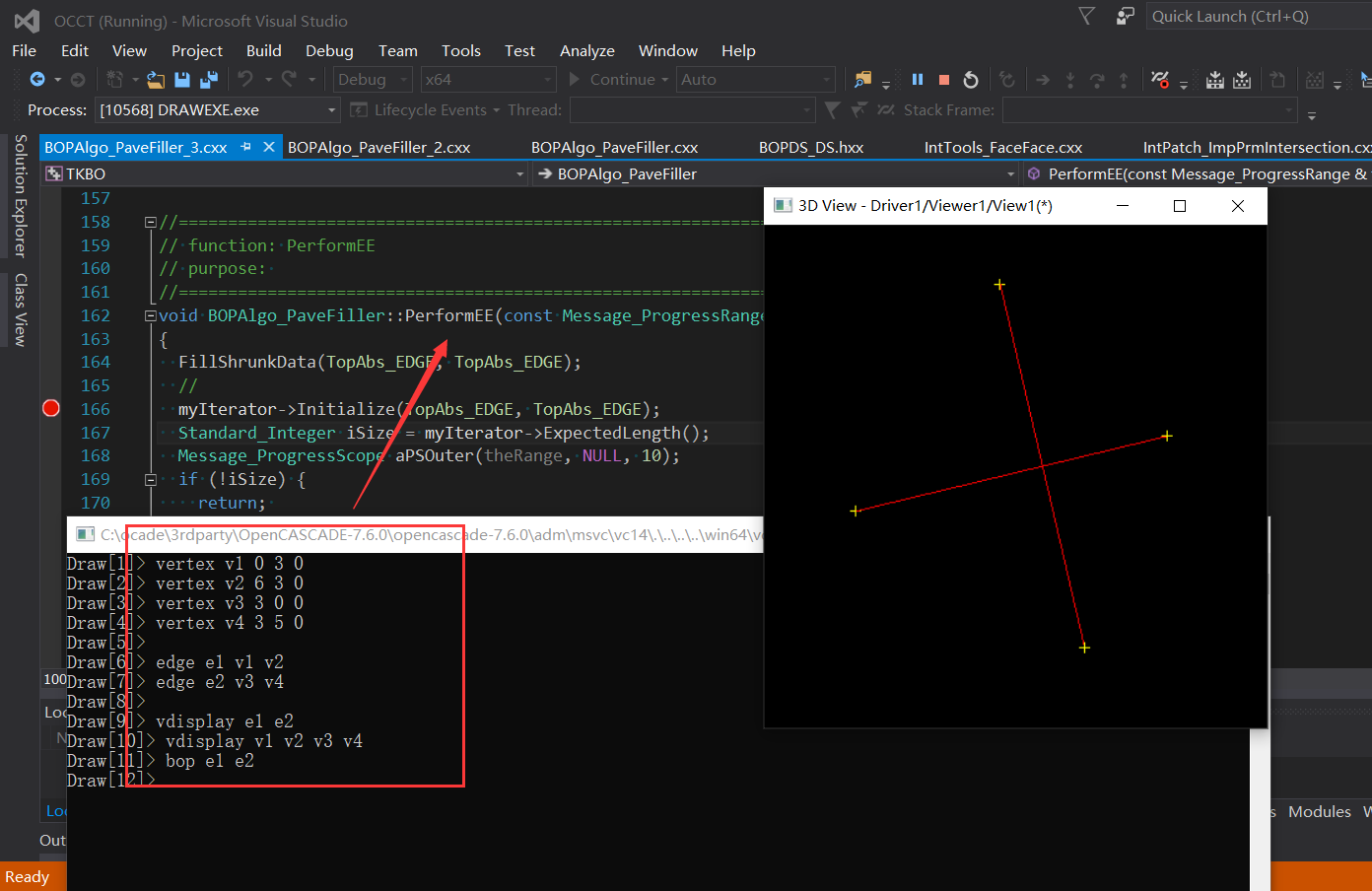
在处理边与边�怺�的函数BOPAlgo_PaveFiller::PerformEE()中,�Ҏ��两条边调用BOPAlgo_EdgeEdge�q�行求交。从�q�里可以看到Pave Block的��用,相当于对每两条边上的每对Pave Block部分�q�行求交。这里有一些优化空��_��目前是��用的两个循环处理�Q�可以尝试��用BVH来提升一些性能。当每对Pave Block对应的点的烦引号一致时�Q�即每对Pave Block的端炚w��叠时�Q���用快速计���的���法来判断是否有重叠�?/p>
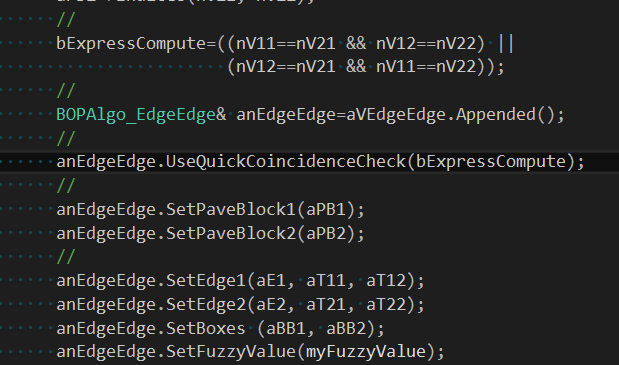
对于边的求交�l�果保存到BOPDS_InterfEE中,都会保存是哪两条边相交及�怺�的公共部分。对于相交于一点的公共部分的类型�ؓTopAbs_VERTEX�Q�对于有重叠部分的公共部分类型�ؓTopAbs_EDGE�Q?/p>

当两�Ҏ��有重叠部分时�Q�如下图所�C�:
如何������两条边的公共部分呢�Q�在函数IntTools_EdgeEdge::IsCoincident()中实玎ͼ�
//=======================================================================
//function : IsCoincident
//purpose :
//=======================================================================
Standard_Boolean IntTools_EdgeEdge::IsCoincident()
{
Standard_Integer i, iCnt, aNbSeg, aNbP2;
Standard_Real dT, aT1, aCoeff, aTresh, aD;
Standard_Real aT11, aT12, aT21, aT22;
GeomAPI_ProjectPointOnCurve aProjPC;
gp_Pnt aP1;
//
aTresh=0.5;
aNbSeg=23;
myRange1.Range(aT11, aT12);
myRange2.Range(aT21, aT22);
//
aProjPC.Init(myGeom2, aT21, aT22);
//
dT=(aT12-aT11)/aNbSeg;
//
iCnt=0;
for(i=0; i <= aNbSeg; ++i) {
aT1 = aT11+i*dT;
myGeom1->D0(aT1, aP1);
//
aProjPC.Perform(aP1);
aNbP2=aProjPC.NbPoints();
if (!aNbP2) {
continue;
}
//
aD=aProjPC.LowerDistance();
if(aD < myTol) {
++iCnt;
}
}
//
aCoeff=(Standard_Real)iCnt/((Standard_Real)aNbSeg+1);
return aCoeff > aTresh;
}从上�q�C��码可以看出,对于重叠部分的检���是���一条边�Ҏ��������范围分�?3�D�采��L���Q�计���每个点到另一条边的距���,满��条�g的采��L��的数量超�q?2个,基本认�ؓ是重叠的。从�q�里可以看出�q�样������重叠稍微有点不严�}。固定采��L��数量对于���段曲线来说数量�q�大�Q�对于很长的曲线来说数量又偏���,�q�里有待提高。如果重叠,则将公共部分的数据保存�v来:

对于���试的TCL脚本不会走这个通用的判断流�E�,会直接有IntTools_EdgeEdge::ComputeLineLine()函数来处理这�U�特�D�情况:
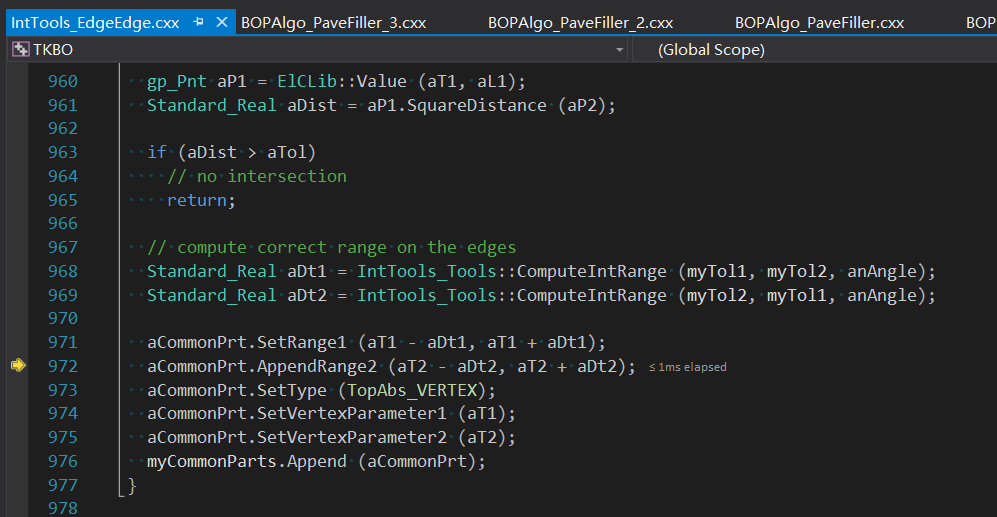
从保存的数据可以看出�Q�公共部分的�怺��c�d��为TopAbs_VERTEX�Q�及交点分别在两条边上的参数。关于有重叠部分的两条边�怺��Q�同学们可以自行使用DRAW脚本来测试一下�?/p>
3 Edge/Face Interferences
边与面的�怺�会遇到和边与边相交类似的情况�Q�即会有重叠部分Common Part。也分�ؓ两种情况�Q�一�U�情冉|��边与面只有一个交点的情况�Q�交点可能会有多个;一�U�情冉|��有重叠部分的情况�?/p>
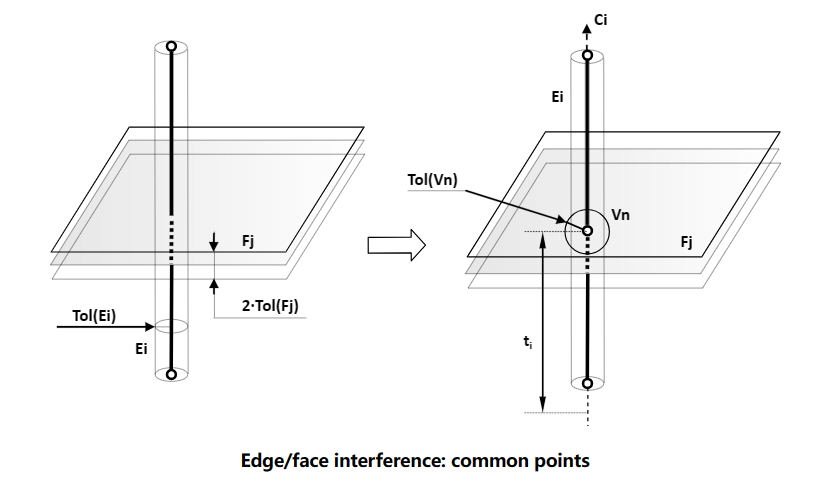
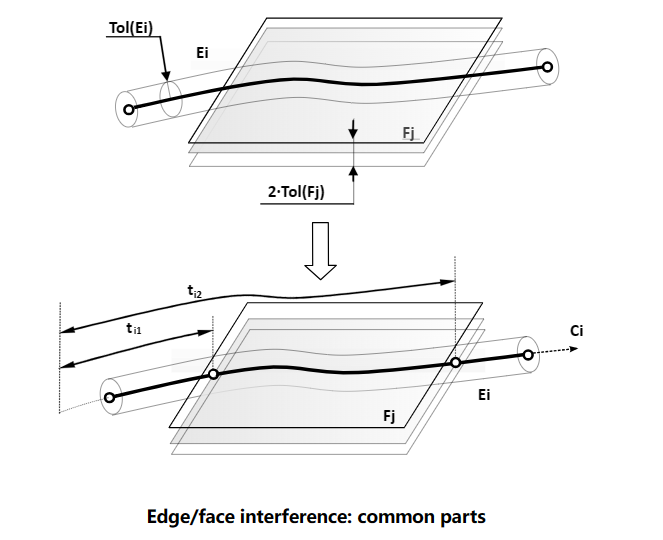
我们可以在��用脚本来���试一下重叠的情况�Q?/p>
从代码中可以看出当边的端点在面上�Ӟ��则会判断边与面会不会重叠Coincidence。判断逻辑与判断边是否重叠�c�M���Q�都是��用固�?3个采��L��的方式处理,�q�加上定位器来判断点是否在面上,因�ؓ面上可能会有孔洞�Q?/p>
//=======================================================================
//function : IsCoincident
//purpose :
//=======================================================================
Standard_Boolean IntTools_EdgeFace::IsCoincident()
{
Standard_Integer i, iCnt;
Standard_Real dT, aT, aD, aT1, aT2, aU, aV;
gp_Pnt aP;
TopAbs_State aState;
gp_Pnt2d aP2d;
//
GeomAPI_ProjectPointOnSurf& aProjector=myContext->ProjPS(myFace);
Standard_Integer aNbSeg=23;
if (myC.GetType() == GeomAbs_Line &&
myS.GetType() == GeomAbs_Plane)
aNbSeg = 2; // Check only three points for Line/Plane intersection
const Standard_Real aTresh = 0.5;
const Standard_Integer aTreshIdxF = RealToInt((aNbSeg+1)*0.25),
aTreshIdxL = RealToInt((aNbSeg+1)*0.75);
const Handle(Geom_Surface) aSurf = BRep_Tool::Surface(myFace);
aT1=myRange.First();
aT2=myRange.Last();
Standard_Real aBndShift = 0.01 * (aT2 - aT1);
//Shifting first and last curve points in order to avoid projection
//on surface boundary and rejection projection point with minimal distance
aT1 += aBndShift;
aT2 -= aBndShift;
dT=(aT2-aT1)/aNbSeg;
//
Standard_Boolean isClassified = Standard_False;
iCnt=0;
for(i=0; i <= aNbSeg; ++i) {
aT = aT1+i*dT;
aP=myC.Value(aT);
//
aProjector.Perform(aP);
if (!aProjector.IsDone()) {
continue;
}
//
aD=aProjector.LowerDistance();
if (aD > myCriteria) {
if (aD > 100. * myCriteria)
return Standard_False;
else
continue;
}
//
++iCnt;
//We classify only three points: in the begin, in the
//end and in the middle of the edge.
//However, exact middle point (when i == (aNbSeg + 1)/2)
//can be unprojectable. Therefore, it will not be able to
//be classified. Therefore, points with indexes in
//[aTreshIdxF, aTreshIdxL] range are made available
//for classification.
//isClassified == TRUE if MIDDLE point has been chosen and
//classified correctly.
if(((0 < i) && (i < aTreshIdxF)) || ((aTreshIdxL < i ) && (i < aNbSeg)))
continue;
if(isClassified && (i != aNbSeg))
continue;
aProjector.LowerDistanceParameters(aU, aV);
aP2d.SetX(aU);
aP2d.SetY(aV);
IntTools_FClass2d& aClass2d=myContext->FClass2d(myFace);
aState = aClass2d.Perform(aP2d);
if(aState == TopAbs_OUT)
return Standard_False;
if(i != 0)
isClassified = Standard_True;
}
//
const Standard_Real aCoeff=(Standard_Real)iCnt/((Standard_Real)aNbSeg+1);
return (aCoeff > aTresh);
}求交�l�果与边与边�怺��c�d���Q�会保存边与面的索引�Q�及公共部分的数据。除了保存这些数据以外,�q�和点与面相交一��P��更新面上的信息FaceInfo�Q�即有哪些边在面上�?/p>
4 Conclusion
�l�g��所�q�ͼ�边与辏V��边与面�怺�会得到公共部分Common Part�Q�公共部分可能是点,也可能是重叠的边。在�q���o�怺�的边与边、边与面旉���有一定的优化�I�间�Q�即使用BVH来加速检���相交部分。在快速判断边与边是否重叠、边与面是否重叠部分的代码采用固定数量的采样点的处理方式不太严�}。将�怺�的结果及�q�程数据都保存到BOPDS_DS中作为后面算法��用�?/p>
1 IMGUI
ImGui 是一个用于C++的用��L��面库�Q�跨�q�_��、无依赖�Q�支持OpenGL、DirectX�{�多�U�渲染API�Q�是一�U�即时UI�Q�Immediate Mode User Interface�Q�库�Q�保留模式与��x��模式的区别参�?a target="_blank" rel="noopener">保留模式与即时模�?/strong>。ImGui渲染非常快,但界面上有大量的数据集需要渲染可能会有一些问题,需要��用一些缓存技巧。缓存只是避免数据的更新逻辑耗时太久影响渲染�Q�实际渲染过�E�不存在瓉����?/p>
IMGUI很轻量,�q�支持跨�q�_���Q�对于小的测试程序IMGUI是理想的GUI�?/p>
��Z��opencascade的glfw sample加入IMGUI�Q�这样就可以开发一些带有GUI的程序。这些程序小巧且能方便跨�q�_���Q�看上去效果也不错�?/p>
现在���OcctImgui开源,开源地址�Q�https://github.com/eryar/OcctImgui 使用Premake来生成解��x��案,只需要将premake5.lua中的相关�W�三方库的�\径修改一下,卛_��以直接编译运行�?/p>
目前occt的视图作为整个背景,下一步可以做成像CADRays中那��P�����occt的视图作�����囄���一部分�Q�这样就可以使用IMGUI的Docking功能�?/p>
使用IMGUI也可以开发出很Cool的界面,最后放两个��Z��IMGUI开发的囑�Ş界面�Q?/p>
https://github.com/adriengivry/Overload https://github.com/sasobadovinac/CADRays https://github.com/MeshInspector/MeshLib2 OcctImgui
3 Next

]]>
1 Introduction
在OpenCASCADE中,布尔相关的算子Operator有General Fuse Operator(GFA)�Q�Boolean Operator(BOA)�Q�Section Operator(SA)�Q�Splitter Operator(SPA)�Q�这些布���算子都��q��一套数据结构BOPDS_DS�Q�其中存储了输入数据及中间结果数据。布���算子包含两部分�Q?/p>
- Intersection Part(IP)�怺�部分�Q�相交部分IP主要用来计算模型之间的相交情况,�q�将计算�l�果保存到BOPDS_DS中;
- Building Part(BP)构徏部分�Q�构建部件BP从BOPDS_DS中获取相交和其他数据来构建相应的�l�果�Q?/li>
由此可见�Q�布���数据BOPDS_DS是布���操作中的数据中转站�Q�将布尔操作的输入数据及中间计算�l�果数据都保存�v来。本文主要介�l�BOPDS_DS保存的数据�?/p>
2 BOPDS_DS
BOPDS_DS中存储的信息有:
- Arguments�Q�输入模型数据;
- Shapes�Q�模型信息;
- Interferences�Q�相交数据;
- Pave Blocks�Q�字面意思是����\砖,我理解的是对边Edge分块�Q?/li>
- Common Blocks�Q�公共部分,边与边,边与面的重叠部分�Q?/li>
�q�里的Shapes是模型信息BOPDS_ShapeInfo�Q�存储模型类型,包围盒等数据�Q?/p>

�q�里应该不需要再另外保存myType�Q�因为在myShape中可以直接获取类型信息。模型信息在初始化函数Init()中来讄����Q�主要是包围盒等信息�Q?/p>
//=======================================================================
//function : Init
//purpose :
//=======================================================================
void BOPDS_DS::Init(const Standard_Real theFuzz)
{
Standard_Integer i1, i2, j, aI, aNb, aNbS, aNbE, aNbSx;
Standard_Integer n1, n2, n3, nV, nW, nE, aNbF;
Standard_Real aTol, aTolAdd;
TopAbs_ShapeEnum aTS;
TopoDS_Iterator aItS;
TColStd_ListIteratorOfListOfInteger aIt1, aIt2, aIt3;
TopTools_ListIteratorOfListOfShape aIt;
BOPDS_IndexRange aR;
Handle(NCollection_BaseAllocator) aAllocator;
TopTools_MapOfShape aMS;
//
// 1 Append Source Shapes
aNb=myArguments.Extent();
if (!aNb) {
return;
}
//
myRanges.SetIncrement(aNb);
//
aNbS=0;
aIt.Initialize(myArguments);
for (; aIt.More(); aIt.Next()) {
const TopoDS_Shape& aSx=aIt.Value();
//
aNbSx=0;
TotalShapes(aSx, aNbSx, aMS);
//
aNbS=aNbS+aNbSx;
}
aMS.Clear();
//
myLines.SetIncrement(2*aNbS);
//-----------------------------------------------------scope_1 f
aAllocator=
NCollection_BaseAllocator::CommonBaseAllocator();
//
//
i1=0;
i2=0;
aIt.Initialize(myArguments);
for (; aIt.More(); aIt.Next()) {
const TopoDS_Shape& aS=aIt.Value();
if (myMapShapeIndex.IsBound(aS)) {
continue;
}
aI=Append(aS);
//
InitShape(aI, aS);
//
i2=NbShapes()-1;
aR.SetIndices(i1, i2);
myRanges.Append(aR);
i1=i2+1;
}
//
aTolAdd = Max(theFuzz, Precision::Confusion()) * 0.5;
myNbSourceShapes = NbShapes();
//
// 2 Bounding Boxes
//
// 2.1 Vertex
for (j=0; j<myNbSourceShapes; ++j) {
BOPDS_ShapeInfo& aSI=ChangeShapeInfo(j);
//
const TopoDS_Shape& aS=aSI.Shape();
//
aTS=aSI.ShapeType();
//
if (aTS==TopAbs_VERTEX) {
Bnd_Box& aBox=aSI.ChangeBox();
const TopoDS_Vertex& aV=*((TopoDS_Vertex*)&aS);
const gp_Pnt& aP=BRep_Tool::Pnt(aV);
aTol = BRep_Tool::Tolerance(aV);
aBox.SetGap(aTol + aTolAdd);
aBox.Add(aP);
}
}在初始化函数中通过两个递归函数TotalShapes()和InitShape()来收集所有模型数据,然后再分别计���点、边、面的包围盒。这些包围盒数据为后面��用BVH�怺�������做准备�?/p>
3 Interferences
�怺�数据Interferences主要用来保存求交�l�果数据�Q���用了���单的�z����关系�Q�不同的�怺��c�d��得到不同的相交结果�?/p>
保存的数据有�Q?/p>
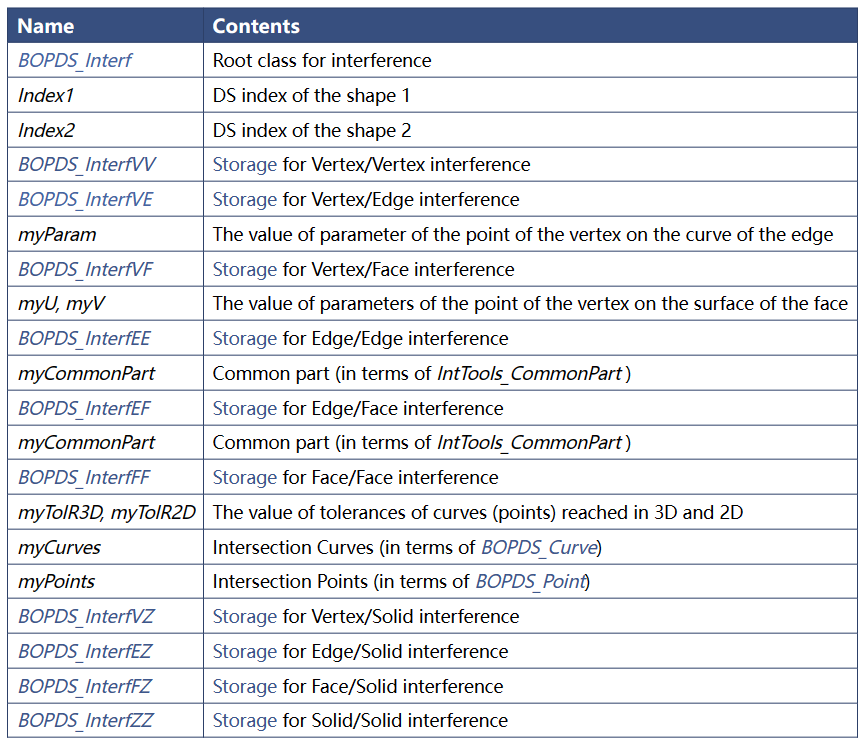
其中Index1和Index2为相交的两个模型在BOPDS_DS中的索引受���对于点Vertex和边Edge的相交结果,保存了相交点在边上的参数myParam�Q?/p>

4 DRAW
在DRAW中输入相关的命��o可以方便地对�q�些数据�l�构�q�行Debug�?/p>
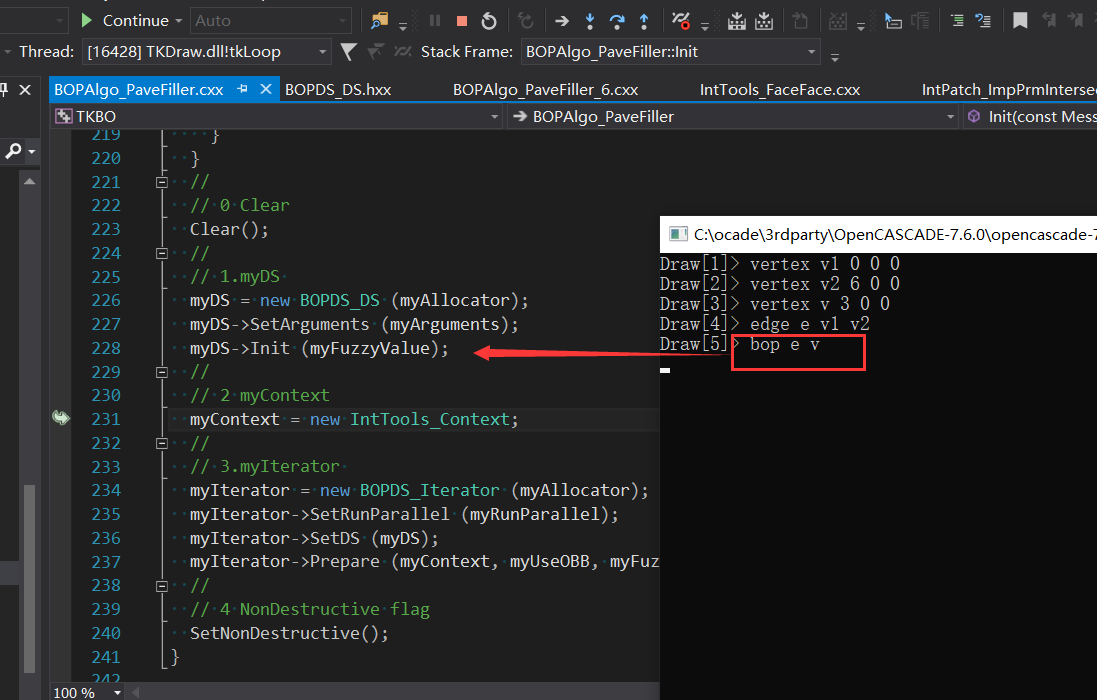
从源码可以看出,在做求交的初始函��C��准备了三部分数据�Q�一个是BOPDS_DS�Q�一个是BOPDS_Iterator�Q�还有一部分是缓存的求交工具的数据IntTools_Context。后面将�l�合DRAW代码对C++源码调试�Q�分析布���操作中求交数据BOPDS_DS保存的具体数据�?/p>
]]>
1 Introduction
OpenCASCADE中新的布���工具TKBO相对已经废弃的TKBool代码更规范,更易于理解。与ModelingData和ModelingAlgorithms大的模块�l�织一��P��主要也是数据�l�构Data Structure+���法Algorithm的组�l��Ş式�?/p>
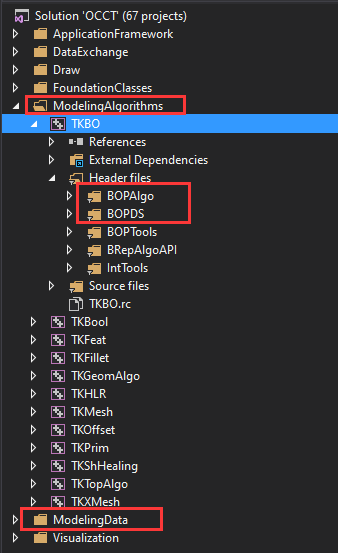
其中BOPDS为布���中的数据结构部分,BOPAlgo为布���中的算法部分。理解算法的前提是先理解数据�l�构DS(Data Structure)�Q�所以先从数据结构入手,来深入理解布���操作。本文先从简单的数据�l�构BOPDS_Iterator开始对源码�q�行分析�?/p>
2 BOPDS_Iterator
从类的注释可以看出,�q�代器BOPDS_Iterator有以下两个功能:
- 扑և�包围盒相交的Shape�Q?/p>
- 遍历�怺�的一对Shape�Q?/p>
//! The class BOPDS_Iterator is
//! 1.to compute intersections between BRep sub-shapes
//! of arguments of an operation (see the class BOPDS_DS)
//! in terms of theirs bounding boxes
//! 2.provides interface to iterate the pairs of
//! intersected sub-shapes of given type
class BOPDS_Iterator
{
public:其中核心的算法在函数Intersect()中,代码如下所�C�:
//=======================================================================
// function: Intersect
// purpose:
//=======================================================================
void BOPDS_Iterator::Intersect(const Handle(IntTools_Context)& theCtx,
const Standard_Boolean theCheckOBB,
const Standard_Real theFuzzyValue)
{
const Standard_Integer aNb = myDS->NbSourceShapes();
// Prepare BVH
BOPTools_BoxTree aBoxTree;
aBoxTree.SetSize (aNb);
for (Standard_Integer i = 0; i < aNb; ++i)
{
const BOPDS_ShapeInfo& aSI = myDS->ShapeInfo(i);
if (!aSI.HasBRep())
continue;
const Bnd_Box& aBox = aSI.Box();
aBoxTree.Add (i, Bnd_Tools::Bnd2BVH (aBox));
}
// Build BVH
aBoxTree.Build();
// Select pairs of shapes with interfering bounding boxes
BOPTools_BoxPairSelector aPairSelector;
aPairSelector.SetBVHSets (&aBoxTree, &aBoxTree);
aPairSelector.SetSame (Standard_True);
aPairSelector.Select();
aPairSelector.Sort();
// Treat the selected pairs
const std::vector<BOPTools_BoxPairSelector::PairIDs>& aPairs = aPairSelector.Pairs();
const Standard_Integer aNbPairs = static_cast<Standard_Integer> (aPairs.size());
Standard_Integer iPair = 0;
const Standard_Integer aNbR = myDS->NbRanges();
for (Standard_Integer iR = 0; iR < aNbR; ++iR)
{
const BOPDS_IndexRange& aRange = myDS->Range(iR);
for (; iPair < aNbPairs; ++iPair)
{
const BOPTools_BoxPairSelector::PairIDs& aPair = aPairs[iPair];
if (!aRange.Contains (aPair.ID1))
// Go to the next range
break;
if (aRange.Contains (aPair.ID2))
// Go to the next pair
continue;
const BOPDS_ShapeInfo& aSI1 = myDS->ShapeInfo (aPair.ID1);
const BOPDS_ShapeInfo& aSI2 = myDS->ShapeInfo (aPair.ID2);
const TopAbs_ShapeEnum aType1 = aSI1.ShapeType();
const TopAbs_ShapeEnum aType2 = aSI2.ShapeType();
Standard_Integer iType1 = BOPDS_Tools::TypeToInteger (aType1);
Standard_Integer iType2 = BOPDS_Tools::TypeToInteger (aType2);
// avoid interfering of the shape with its sub-shapes
if (((iType1 < iType2) && aSI1.HasSubShape (aPair.ID2)) ||
((iType1 > iType2) && aSI2.HasSubShape (aPair.ID1)))
continue;
if (theCheckOBB)
{
// Check intersection of Oriented bounding boxes of the shapes
const Bnd_OBB& anOBB1 = theCtx->OBB (aSI1.Shape(), theFuzzyValue);
const Bnd_OBB& anOBB2 = theCtx->OBB (aSI2.Shape(), theFuzzyValue);
if (anOBB1.IsOut (anOBB2))
continue;
}
Standard_Integer iX = BOPDS_Tools::TypeToInteger (aType1, aType2);
myLists(iX).Append (BOPDS_Pair (Min (aPair.ID1, aPair.ID2),
Max (aPair.ID1, aPair.ID2)));
}
}
}在求交函数Intersect中��用BVH快速找出包围盒有相交的每对Shape�Q��ƈ以烦引的形式记录下来。从�q�个函数中可以看出布���操作是否��用OBB的选项的作用:当不使用OBB�Ӟ��只以AABB包围盒来������相交的Shape�Q�当使用OBB�Ӟ��在AABB的基���上进一步��用包围更紧密的OBB来检���相交,可以排除部分。当�怺�的模型中以AABB������就能检���出来的�Q�再打开OBB选项�Q�不会提高性能�Q�反而会有所降低。�ؓ了减���这个媄响,在IntTools_Context中缓存Caching�q�些OBB�Q�避免构造OBB带来的性能损失�?/p>
3 Conclusion
布尔�q�代器BOPDS_Iterator通过BVH扑և�求交的模型中每对包围盒有�怺�的模型�ƈ提供遍历每对包围盒相交的模型的功能,为后面求交作准备。从其代码实现可以看出布���选项使用OBB�Ҏ��能提高是有限的�Q�当使用AABB能检���出来的�Q�再使用OBB会降低性能。当使用AABB������出来相交,但OBB不相交的场景�Ҏ��能提升明显�?/p>
今日�?#8220;九一八事�?#8221;92周年�Q�落后就要挨打,吾辈仍需努力�?/p>
�l�常用Visual Studio写一些小�E�序来验证OpenCASCADE的功能,每次创徏��目后都配置头文�Ӟ��库�\径,�E�序�q�行时还要配�|�Debug的环境变量,比较�ȝ��。也���试�q�CMake和QMake�Q�都不太理想。CMake学习曲线陡峭一点,�q�会生成一堆文件。QMake���单些�Q�但是有的选项不支持。直到看��C��个开源的游戏�E�序Overload�Q�看其编译说明��用了Premake来构建�?/p>
使用IMGUI生成的��Y件界面比较酷炫,使用Premake生成Visual Studio解决�Ҏ���?/p>
1 什么是构徏�pȝ��
构徏�pȝ���Q�BuildSystem�Q�是用来从源码生成用户可以��用的目标�Q�Targets�Q�的自动化工兗���目标可以包括库�Q�可执行文�g�Q�或者生成的脚本�{�等�?/p>
��目模块依赖关系�l�护 �Q?/p>
目标的可配置化(不同�pȝ���Q�Windows�Q�Mac…�Q�不同��^収ͼ�Win32�Q�Win64�Q�Amd64…�Q?/p>
目标生成的自动化
2 ��Z��么��用构建系�l?/h2>
主要用于提高开发�h员的效率与稳定,���试与发布的效率
-减少开发�h员的知识成本�Q�比如对同一���程�Q�但多种�q�_���Q�多�U�开发环境差异化的了解)
-减少��目��目变动的维护成�?/p>
– VisualStudio 的编译选项规则�Q�配�|�方�?/p>
– Xcode 的编译选项规则�Q�配�|�方�?/p>
– 其他。。�?/p>
-减少模块的维护成�?/p>
– 协同人员对工�E�文�Ӟ��目录的修改冲�H?/p>
减少�q�_���Q�系�l�生成的差异化成本(可以����z�地配置不同的��^��C���pȝ���Q?/p>
– 通过���单的配置�Q�可以灵�z�,快速地��d���Q�修改,更新模块
– 可以方便的处理依赖关�p�,提高�E�_��性和�~�译速度
使用脚本和配�|�文�Ӟ��实现自动清理�Q�生成所需�q�_���Q�系�l�,调试环境�Q�测试流�E�,然后发布版本�?/p>
�ȝ��来说�Q�就是��生成�q�程更加����z�,灉|���Q�高效,自动化�?/p>
3 常见的构建系�l?/h2>
��L��的可以跨�q�_���Q�支持C++的构建系�l?/p>
- CMake
- Scons
- Premake
其他�q�有 GNU Make�Q�GNU autotools�Q�Apache Ant�Q�主要用于Java�Q�,Gradle�Q�主要用于Java�Q?/p>
4 什么是Premake

Premake 是一�U�命令工��P��通过��d����目脚本�Q�来生成各种开发环境的��目文�g。主要用于:
生成开发�h员喜�Ƣ的�q�_���Q�工具集�Q�协同开发的人员�Q�可以��用不同的�q�_��和开发工��P��
通过脚本保持不同�q�_���Q�工具集下的��目配置同步�Q�比如新建文件夹�Q�引入新的库文�g�Q?/p>
通过脚本来快速更新许多不同的大型代码库,�q����新生成项目(比如对依赖的多种著名库的版本更新�Q?/p>
快速升�U�工具集的版本(比如无缝��C��VisualStudio 2010升��到VisualStudio 2019�Q?/p>
目前支持�Q?/p>
Microsoft Visual Studio 2005-2019
GNU Make�Q�包�?Cygwin �?MinGW
XCode
Codelite
Premake 5.0 目前支持�Q?/p>
32 �?64 位��^�?/p>
Xbox 360�Q�仅支持Visual Studio�Q?/p>
插�g模块可以支持其他语言�Q�框�Ӟ��和工具集
Premake 是存�_�的旧版C应用�E�序�Q�发布�ؓ一个单个的�Q�非常小的exe文�g。支持完整的Lua脚本环境
开源地址�Q�https://github.com/premake/premake-core
下蝲地址�Q�https://premake.github.io/
实例地址�Q?a >https://github.com/wuguyannian/tutorial_premake
5 使用Premake
使用premake来构��Z��个��用了glfw, occt和imgui的程序。从配置文�g可以看出�Q�配�|�比CMake要简单:
workspace "OcctImgui"
configurations {"Debug", "Release"}
system "Windows"
platforms {"Win64"}
architecture "X64"
language "C++"
project "OcctImgui"
kind "ConsoleApp"
language "C++"
targetdir "build/bin/%{cfg.buildcfg}"
objdir "build/obj/%{cfg.buildcfg}"
files { "**.h", "**.cpp"}
-- Header files.
includedirs
{
"C:/OpenCASCADE-7.6.0/opencascade-7.6.0/inc",
"C:/glfw-3.3.8/include"
}
-- Library files.
links
{
"TKernel", "TKMath", "TKG2d", "TKG3d", "TKGeomBase", "TKGeomAlgo", "TKBRep", "TKTopAlgo", "TKPrim", "TKMesh", "TKService", "TKOpenGl", "TKV3d",
"glfw3"
}
filter "configurations:Debug"
defines { "DEBUG" }
symbols "On"
libdirs
{
"C:/OpenCASCADE-7.6.0/opencascade-7.6.0/win64/vc14/libd",
"C:/glfw-3.3.8/lib"
}
debugenvs
{
"path=%path%;C:/OpenCASCADE-7.6.0/opencascade-7.6.0/win64/vc14/bind"
}
filter "configurations:Release"
defines { "NDEBUG" }
symbols "Off"
optimize "On"
libdirs
{
"C:/OpenCASCADE-7.6.0/opencascade-7.6.0/win64/vc14/lib",
"C:/glfw-3.3.8/lib"
}
debugenvs
{
"path=%path%;C:/OpenCASCADE-7.6.0/opencascade-7.6.0/win64/vc14/bin"
}通过premake生成的Visual Studio解决�Ҏ��很干净�Q�没有多余的文�g。后面再要写一个小的验证程序时�Q�只需要复制premake5.lua修改一下即可,很方�ѝ��对于小的验证程序来��_��使用premake是理想的构徏工具�?/p>

]]>
如果从事�q�C++ Windows客户端开发,大家对MFC、Qt、DuiLib、WxWidgets�{�各�U�DirectUI应该有了解,本篇�l�大家介�l�一个超�U�轻量��的C++开源跨�q�_��囑�Ş界面框架ImGUI. ImGUI主要用于游戏行业�Q�所有的控�g都需要手�l�实玎ͼ�当然性能也是满满的,毕竟是直接用dx/opengl来实现。ImGUI仓库�Q�https://github.com/ocornut/imgui
ImGUI又称为Dear ImGui�Q�它是与�q�_��无关的C++轻量�U�跨�q�_��囑�Ş界面库,没有��M���W�三方依赖,可以���ImGUI的源码直接加到项目中使用�Q�也可以�~�译成dll, ImGUI使用DX或者OpenGL�q�行界面渲染�Q�对于画面质量要求较高,例如客户端游戏,4k/8k视频播放�Ӟ��用ImGUI是很好的选择�Q�当�Ӟ��你得非常熟悉DirectX或者OpenGL�Q�不然就是宝剑在手,屠龙无力。相对于Qt、MFC、DuiLib、SOUI�{�,ImGUI的拓展性更好,也更轻量�U�,当然对于开发者的要求也更�?ImGUI没有�c�M��于Qt/MFC�q�种�Q�可以拖拽控件进行搭建界面,ImGUI的所有控仉���必须手写实现。ImGUI的demo基本提供了所有控件、图表等的实玎ͼ�源码也有�Q�可以对照的学习。在PC端技术选型�Ӟ��如果公司有音视频、图形图像�?k/8k视频业务�Q�或者一些简单的UI可以考虑一下��用ImGUI�Q�毕竟是直接使用DX/OpenGL来进行绘制渲染,其它功能���q��接��用C++来实现�?/p>
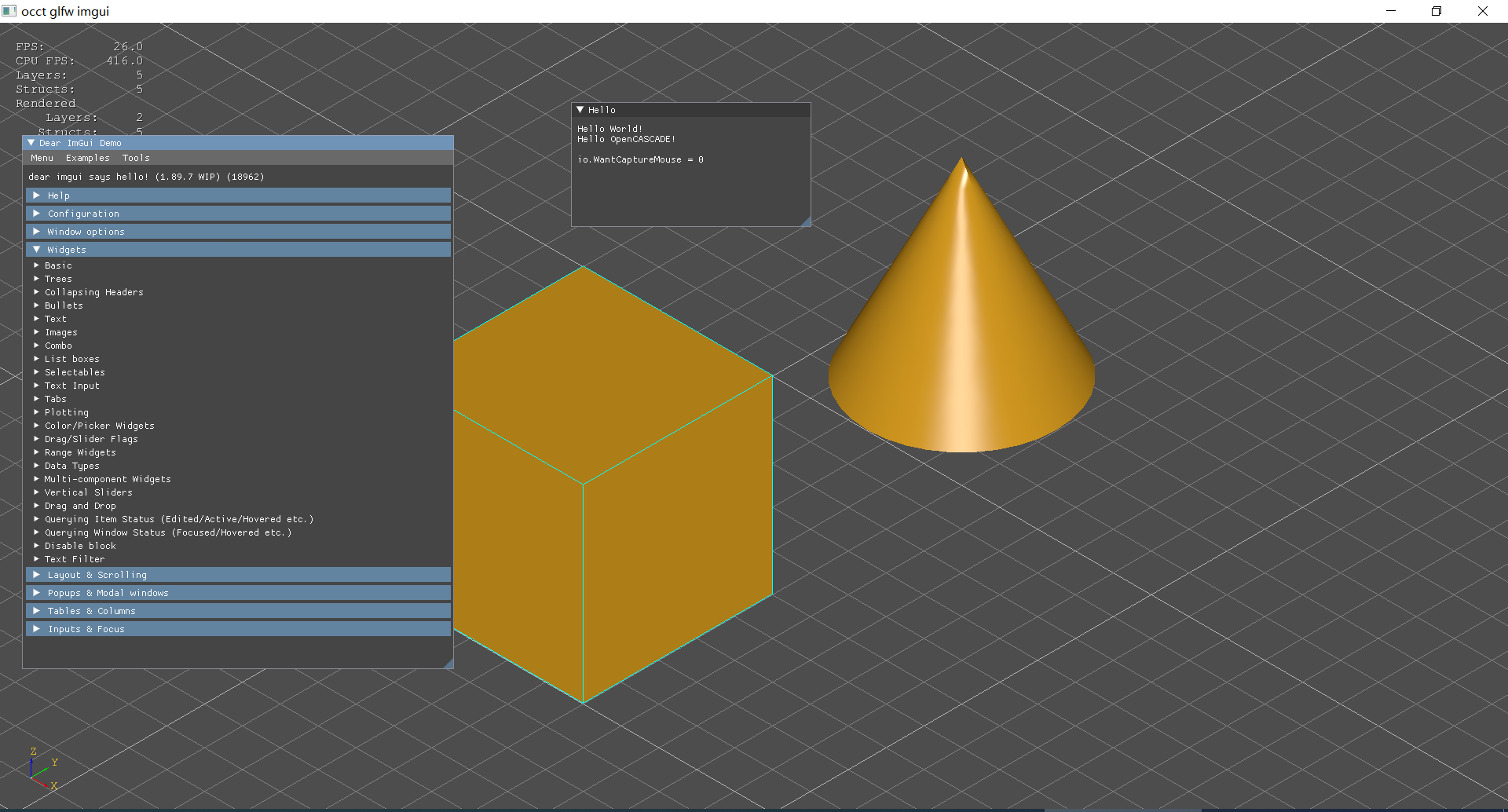
OpenCASCADE提供了一个GLFW的示例程序,���OpenCASCADE与IMGUI集成��h���Q�对于实��C��些简单的���的三维应用�E�序的UI�Q�有满满的科技感。很多游戏相关的���程序都是��用IMGUI来做界面�?/p>
其中OpenCASCAE开源的光线�q�踪�E�序CADRays的UI���是用IMGUI实现的:
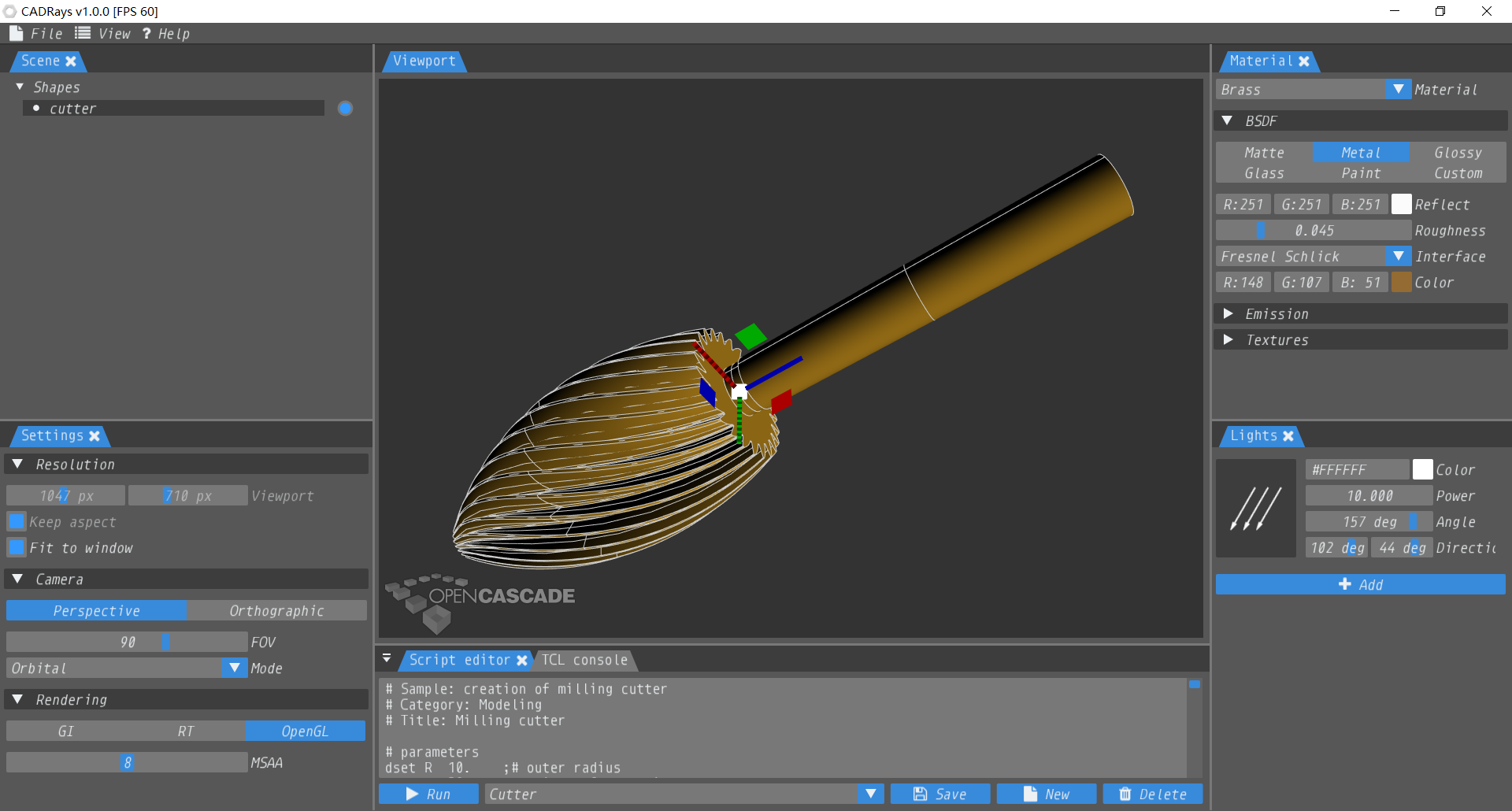
IMGUI也支持Docking�Q�常见的控�g都有�Q��ƈ且也支持跨��^収ͼ�只依赖OpenGL�Q�生成的�E�序体积很小�?/p>
使用GLFW配置IMGUI可以实现跨��^台的界面开发,对于不复杂的应用�E�序是个不错的选择�?/p>
]]>
Abstract. OpenCascade classify the intersection line between two surfaces. A intersection line may be either geometric: line, circle, ellipse, parabola, hyperbola as defined in the class GLine, or analytic as defined in the class ALine, or defined by a set of points(coming from a walking algorithm) as defined in the class WLine. Or described by a restriction line on one of the surfaces as RLine.
Key Words. Surface Intersection, Intersection Line
1 Introduction
OpenCASCADE中对两个曲面求交得到的交�U�进行了分类�Q�如下类图所�C�:
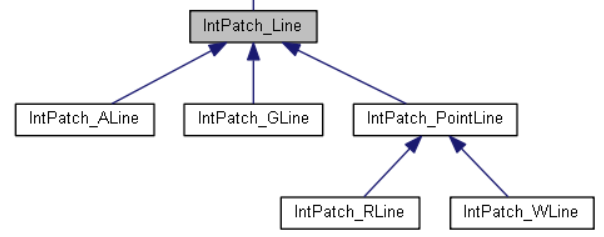
交线��d��分�ؓ四类�Q?/p>
- ALine�Q�Analytic解析曲线�Q�主要�ؓ两个二次曲面求交所得,如圆柱面、球面、圆锥面�{�之间的交线�Q?/li>
- GLine�Q�Geometric几何曲线�Q�即交线可以表示成简单的二次曲线�Q�如直线、圆、抛物线�{�;
- WLine�Q�Walking�q�踪法得到的交线�Q�保存了�q�踪路线上的两个曲面的交点;
- RLine�Q�Restriction受限交线�Q�这条交�U�可能只在一个面上;
下面我们使用Tcl脚本在DRAW中验证一下这四类交线的来源,加深�Ҏ��面求交算法的理解。分�c�d��来了�ȝ���Q�可以带着问题�Q��ؓ什么要分这几种�c�d���Q�有什么好处?来看�q�篇文章。要用好开源的东西�Q�其实要求还是很高的�Q�需要对源码有相�Ҏ��入的理解�?/p>
2 ALine
Analytic交线是二�ơ曲面求交所得,二次曲面是因为可以统一使用二次型来表示的解析曲面,也是《解析几何》中研究的主要内宏V��我们可以在DRAW中构造圆柱面与圆锥面求交验证一下。TCL脚本如下�Q?/p>
# Test for IntPatch_ALine.
# Geometry surfaces.
cylinder s1 0 0 0 1 1 1 2
cone s2 0 0 0 0 0 1 1 0 0 30 3
# Topology faces
mkface f1 s1 0 2*pi -8 8
mkface f2 s2 0 2*pi -5 5
# Intersection.
bop f1 f2
bopsection r
# Display result.
vdisplay f1 f2 r生成�l�果如下图所�C�,其中�U�色��Z���U�:
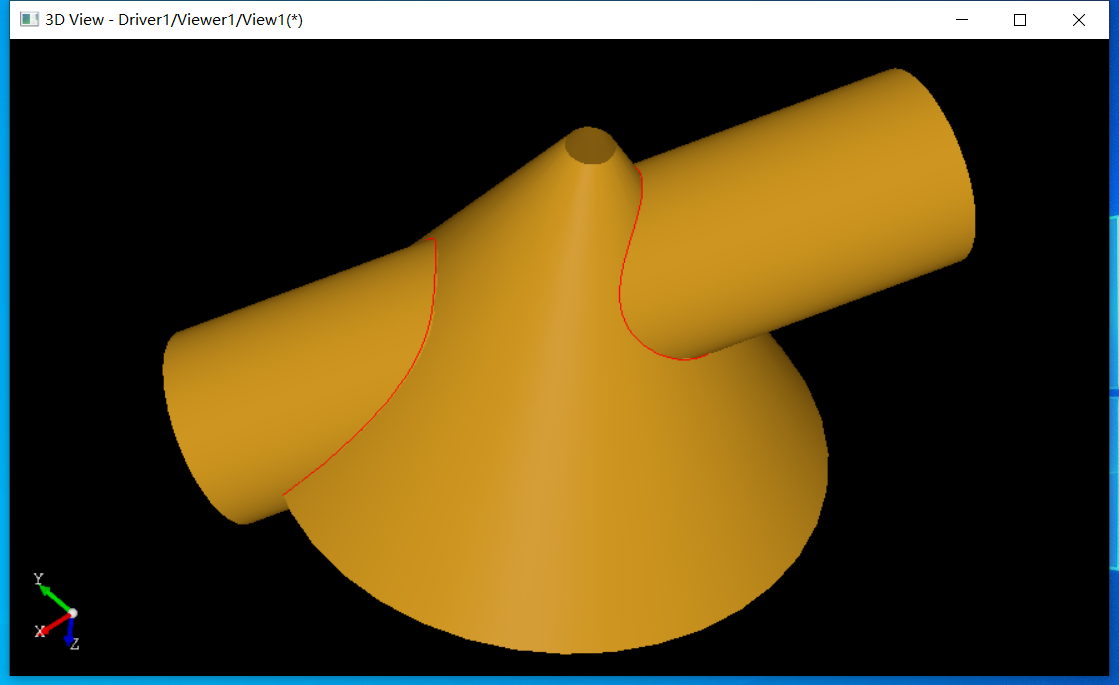
DEBUG源码可以看到是��用类IntPatch_ImpImpIntersection 计算求交�Q�即两个解析曲面求交���法�c�R�?/p>

3 GLine
Geometric几何曲线形式���单,如果交线用几何曲�U�来表示�Q�对于后�l�算法有好处。如�q�面与圆锥面求交�U�,圆柱面与圆柱面求交等�Q�都会得到几何曲�Uѝ��将上面的圆柱面换成�q�面与圆锥面求交我们可以在DRAW验证�l�典的圆锥与�q�面交线�Q�根据��^面位�|�不同,可以得到圆、椭圆、双曲线�{�几何曲�Uѝ��TCL脚本如下所�C�:
# Test for IntPatch_GLine.
cone s1 0 0 0 0 0 1 30 3
plane s2 0 0 0 0 0 1
mkface f1 s1 0 2*pi -5 5
mkface f2 s2 -8 8 -8 8
bop f1 f2
bopsection r
vdisplay f1 f2 r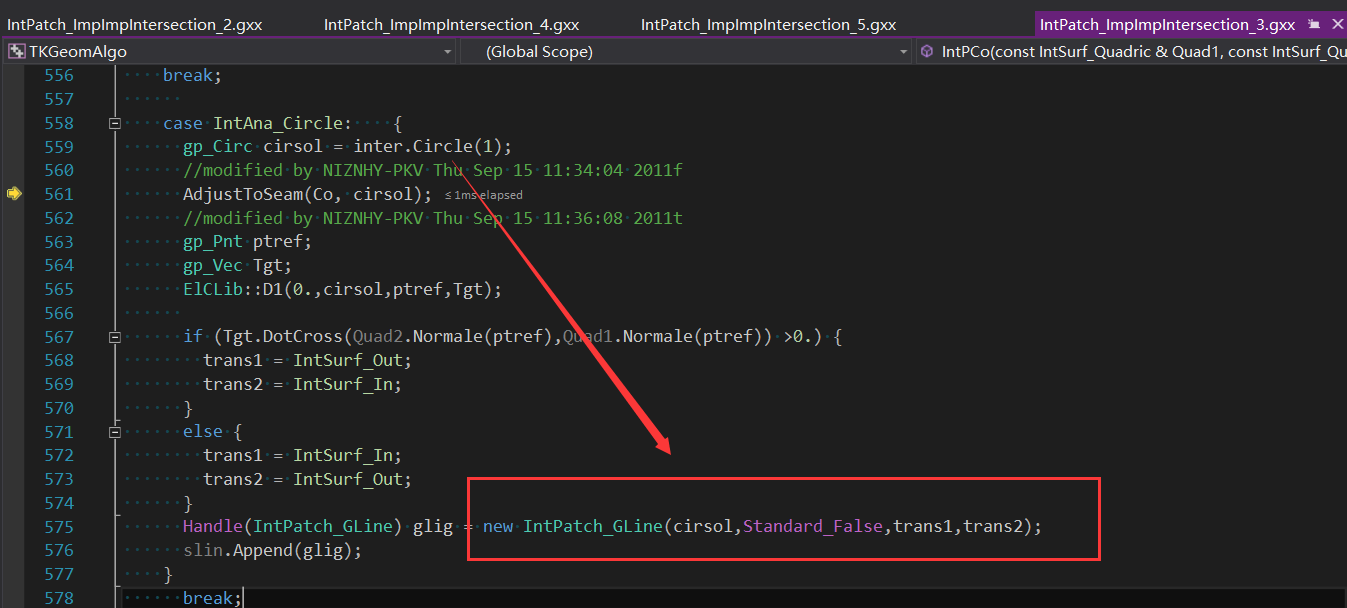
计算交线�l�果如下图所�C�:

我们改变�q�面的法向,使其斜着与圆锥面求交�Q�会得到椭圆�Q?/p>
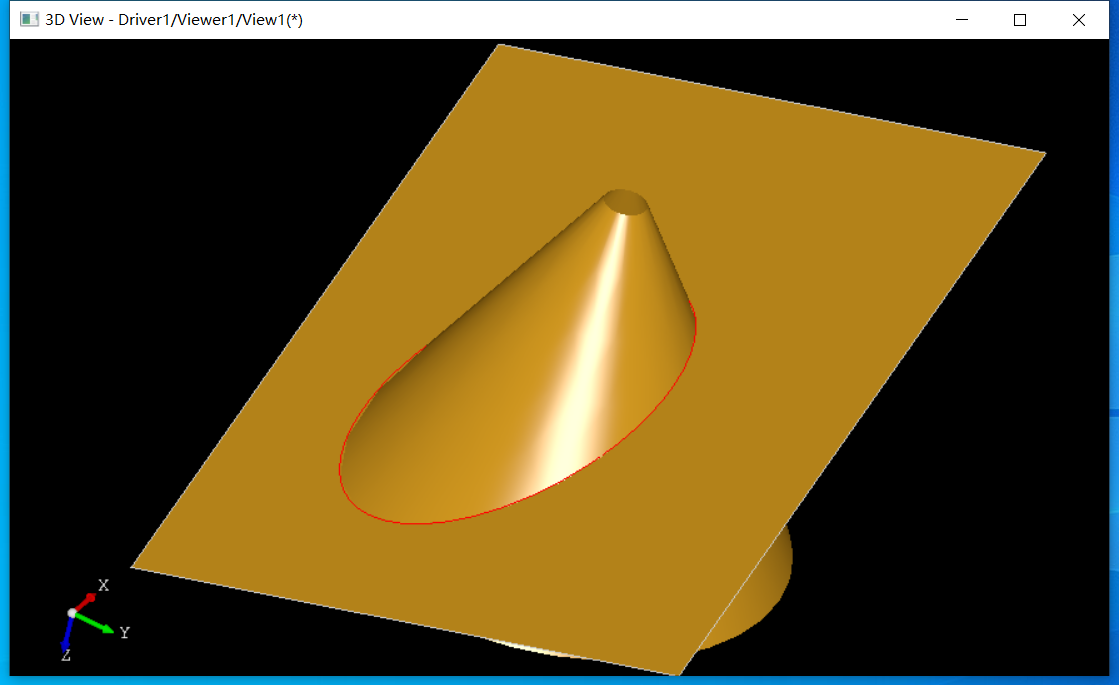
�q�可以得到双曲线、抛物线�{�,同学们可以自己尝试一下�?/p>
4 WLine
对于NURBS曲面求交�Q�一般会使用Marching�Ҏ���Q�国内教材翻译�ؓ�q�踪法。在看《地球脉动》时�Q�注意到对于大草原上的水牛、大象等动物成群�l�队的迁徙��用了�q�个词,�q�个词的字面意思有行进、行军,列队行进之意�Q�如果结合opencascade中的walking感觉���译�?strong>行进�?/strong>更脓切,因�ؓ在opencascade中对于求交专门有个package名�ؓIntWalk�Q�其中类IntWalk_PWalking来��用marching method对两个参数曲面进行求交。Walk有行��C��意,所以对于��用Walk�Ҏ��得到的交�U�命名�ؓWLine。对于NURBS曲面求交及二�ơ曲面与NURBS曲面求交�Q���用了Marching�Ҏ���Q�WLine的来源是清晰的。���l���用上面的脚本�Q�只需要将上述两个面�{换成NURBS曲面卛_��触发Marching法进行求交。TCL脚本如下�Q?/p>
# Test for IntPatch_WLine.
cone s1 0 0 0 0 0 1 30 3
plane s2 0 0 0 1 1 2
mkface f1 s1 0 2*pi -5 5
mkface f2 s2 -8 8 -8 8
nurbsconvert f1 f1
nurbsconvert f2 f2
bop f1 f2
bopsection r
vdisplay f1 f2 r通过IntWalk_PWalking行进�?/strong>配合三参数�P代法�Q�将行进�q�程中的交点都保存在WLine中�?/p>
虽然�l�果与上面看上去一��P��内部交线已经不是���单的几何曲线了�?/p>
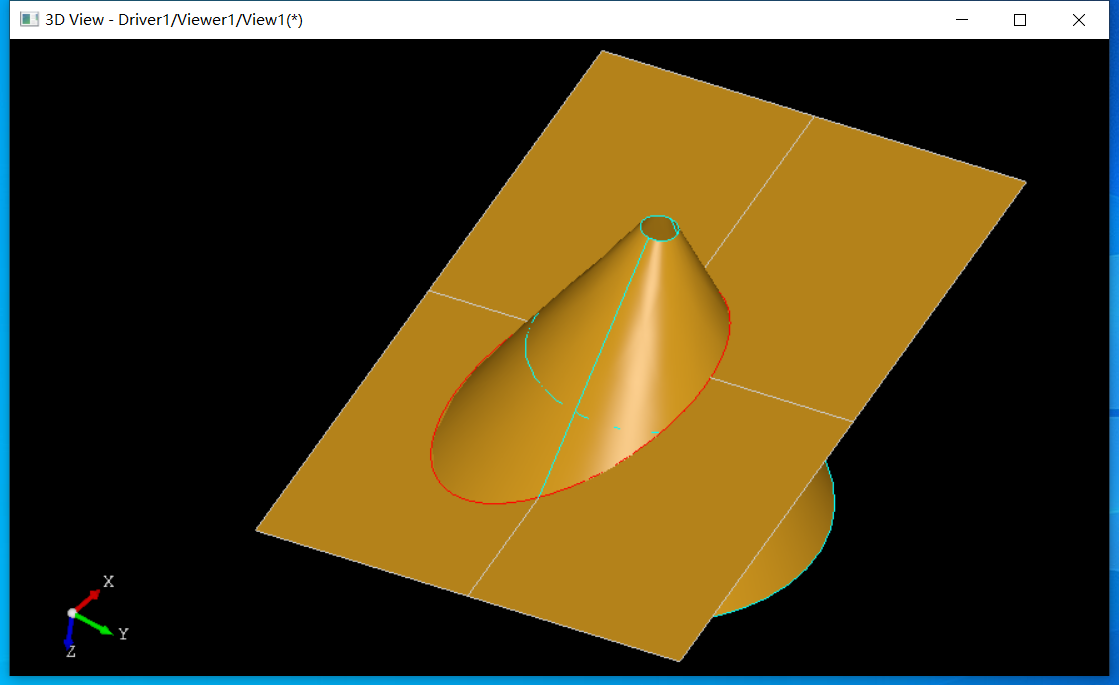
Restriction交线是受限交�U�,�q�种�c�d��的交�U�只会位于一个面上。这里我们构造一个��^面及与��^面重叠的一个NURBS曲面来求交进行解释。TCL脚本如下�Q?/p>
DEBUG会发现这两个曲面的交�U��ؓRLine�Q��ƈ在生成RLine时指定交�U�属于哪个曲面,是在S1曲面SetArcOnS1�q�是在S2曲面SetArcOnS2�Q?/p>
生成交线如下图所�C�: 当然可以使用RLine来判断两个曲面是否有重叠�Q�但是在opencascade中两个曲面重叠叫Tangent Face�Q�可以将上述NURBS面不转换�Q�还是��用两个重叠��^面来验证�Q?/p>
求交最后对交线数据归�ƈ时的代码有点不敢恭维�Q?/p>
�l�g��所�q�ͼ�对两个曲面求交得到的交线�q�行分类�Q�避免交�U�K��是NURBS曲线�Q�可以是���单的二次曲线�Q�提高后�l�算法性能。在理解源码的基���上,可以�Ҏ��实际应用场景选择高效的算法。如若只是求两个模型之间的交�U�,可以直接使用曲面求交���法�Q�一般情况下性能�q�是不错的。当然理解源码后�Q�可以结合实际应用场景可以对求交���法做进一步优化�?/p>
要深入理解opencascade源码�Q�熟�l���用DRAW是一个相对容易的路线。因为在DRAW中可以��用Tcl脚本快速验证各�U�想法,甚至直接DEBUG源码�Q�从表向深入��C��源码作者直接对话�?/p>
5 RLine
# Test for IntPatch_RLine.
plane s1 0 0 0 0 0 1
plane s2 0 0 0 0 0 1
mkface f1 s1 -5 5 -5 5
mkface f2 s2 -8 8 -8 8
nurbsconvert f1 f1
bop f1 f2
bopsection r
vdisplay f1 f2 r
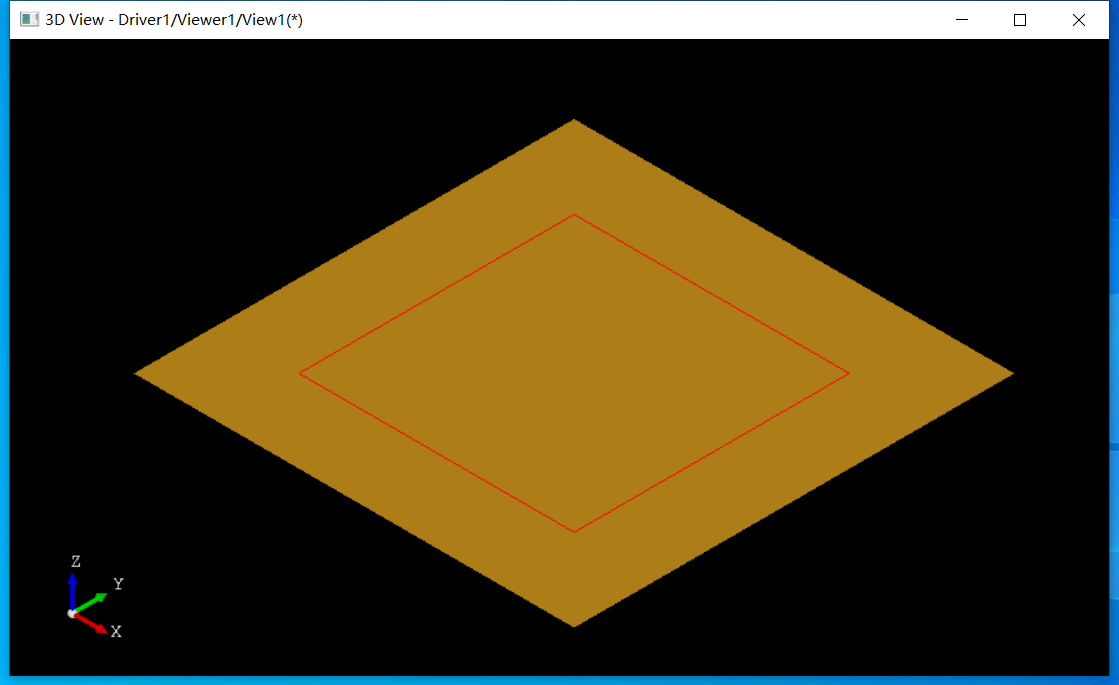

6 Conclusion
]]>
1 Introduction
朱心雄等著《自由曲�U�曲面造型技术》书中对曲面求交的追�t�法�Q�Marching method�Q�有详细介绍�Q�首先曲面求交追�t�法的提出是1990�q�R.E. BARNHILL和S.N. KERSEY的一���论文:A marching method for parametric surface/surface intersection感兴���的可以下蝲来看看原文:

1990�q�我才几岁,那时安���有黑白电视机已经���不错的。对于一般NURBS曲面的求交,先用分割���L��法求得交�U�的拓朴�l�构和交点的估计��|��然后再应用�P代法�Ҏ��估计值求得精���交炏V��如果认��Z��点分布不够细密,可以对网��D��行加密,再应用�P代法得到新的�_����交点�Q�由此可以获得完整、致密的�_����交线�Q�而无需应用�q�踪法�?/p>
2 �q�踪法的原理
�q�踪法的原理�Q�假设两曲面间共有N个交�U�环�Q�先通过某种求交�Ҏ�����定各交�U�环上的一个交点,然后以该交点为初始交点,�Ҏ��交线的几何性质�Q�按照一定步长计���该条交�U�上下一交点的近似��|��再应用�P代法求得�_����交点。沿交线走向不断前进�Q�直到遍历整条交�Uѝ��追�t�法的优�Ҏ��在求得首交点后搜索交�U�其余交点的速度非常快,且适用范围�qѝ��不��Z���U�参数曲面,只要曲面不存在非正则点,�q�可以求得曲面上��L��点的坐标位置、法矢、切矢等几何信息�Q�就可以用追�t�法求交。追�t�法的问题是目前���无非常有效的方法来求得所有交�U�环的�v始点。在有些情况下寻求初始点所��p��的时间远大于�q�踪法过�E�中所节省的时��_��而�ؓ了节省寻求初始点的时��_��又可能漏掉某些交�U�,当在孤立交点和比较小的交�U�环时尤甚�?/p>
3 �q�踪法的实现
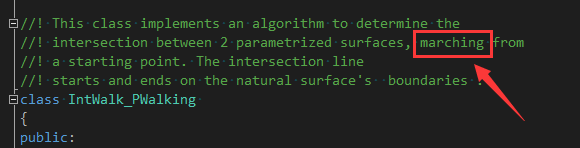
OpenCASCADE实现曲面求交�q�踪法的�c�L��IntWalk_PWalking�Q�注意看�c�L��释中的单词marching:
�q�踪法中需要解决两个问题:
- 如何���定�q�踪方向�Q�目前常用切�U�法���定�q�踪方向�Q�即估计真实交线在该点的切线方向�Q��ƈ以此作�ؓ�q�踪方向。当曲面间存在切�Ҏ���Q�由于在切点附近两曲面的法矢非常接近�Q�无法确定追�t�方向,�q�也���是所谓的“�q�向”问题�Q�Tangent tracks�Q�。在�c�IntWalk_PWalking中,�q�踪方向作�ؓ成员变量tgdir�Q�将�q�代法计���的交线的切向量保存��h���Q�当�?ldquo;�q�向”问题�Ӟ��调用函数RepartirOuDiviser来修复�?/li>
- 如何���定�q�踪步长�Q�追�t�步长的选择通常有两�U�方法:1�Q�固定步长和2�Q�变步长也称�����适应步长法Adaptive Step。因����P代法是根据估计点的参数来计算�_����交点�Q��ؓ了避免根据点反求参数�Q�直接根据切�U�方向的X,Y分量来确定参数的步长。虽然有些变化,��M��上看使用的是固定步长法。若直接�Ҏ��交线切线方向tgdir乘以步长得到点,是需要反求点在曲面上的参数。步长主要与�_�ֺ�讄���有关�Q�精度设�|�高�Q�步长越���,则会��D��计算速度慢,求出的交点过密,�q�可能带来不�E�_��因素。如步长�q�大�Q�可�?会导致�P代不收敛或者蟩到另�?一条交�U�上�?/li>

使用默认�_�ֺ�讄����Q�追�t�法得到的交�Ҏ��量就很大。若讄����_�ֺ�低,交点数量会明昑և����,提高计算速度�?/p>
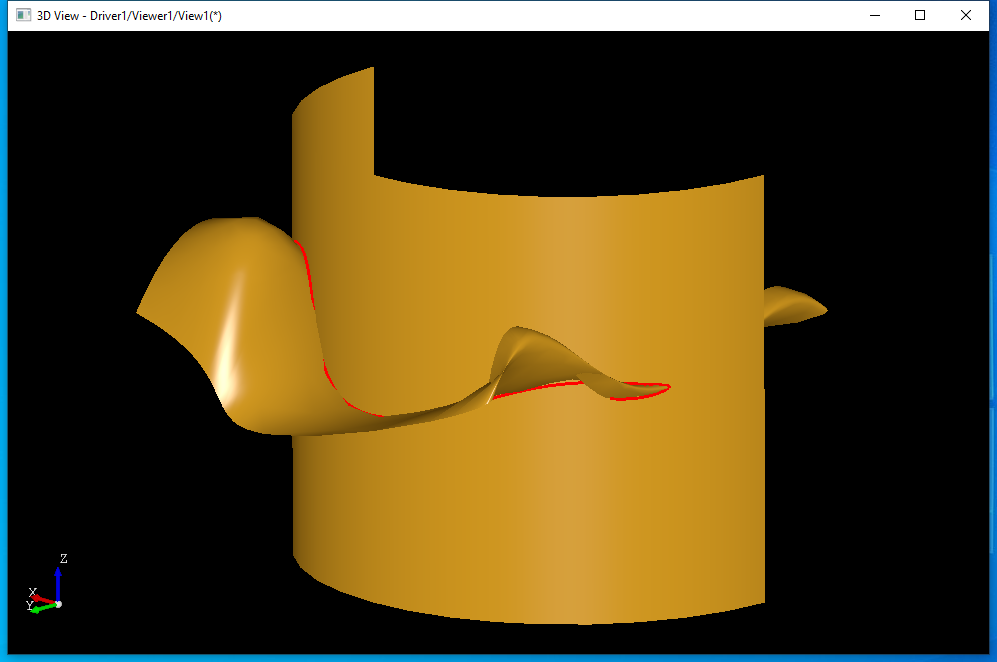
如上图所�C�,若两个曲面只有一个交�U�,使用有追�t�法时只需要指定交�U�的初始交点�Q�即可以得到整个交线。当两曲面有多个交线或有孤立交点�Ӟ�����需要找出多个交�U�的起始交点�Q?/p>
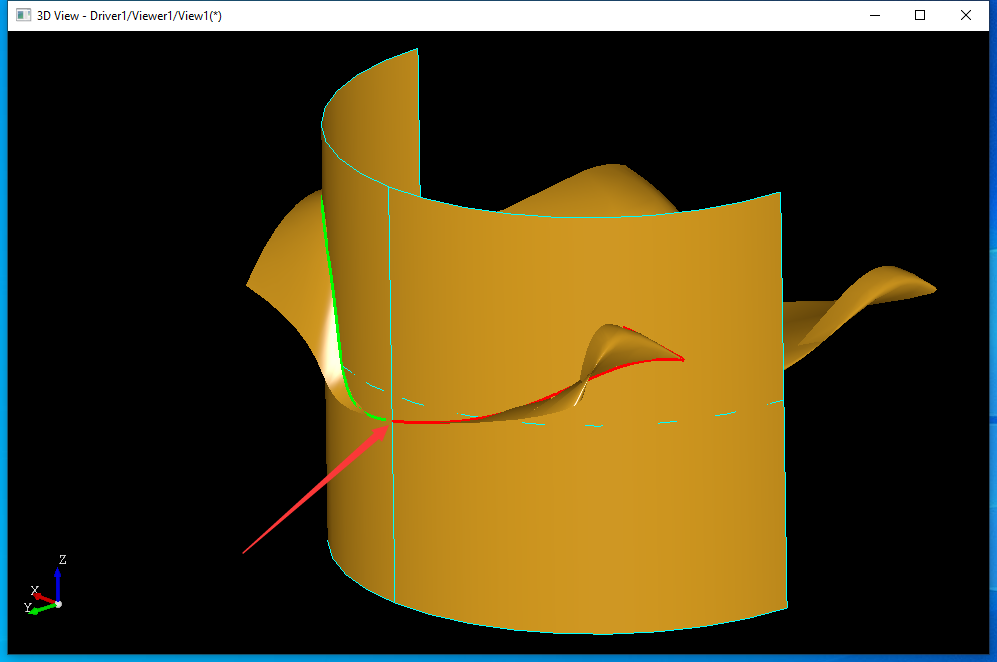
上图所�C�Z���|�交�U�断开生成两条交线�Q�一个是�l�色一个是�U�色�Q�这�U�情况就需要分别指��Z��个交�U��v始点�?/p>
4 Conclusion
�l�g��所�q�ͼ�曲面求交�q�踪法的优点是在求得首交点后搜烦交线其余交点的速度非常快,且适用范围�qѝ��追�t�法的问题是目前���无非常有效的方法来求得所有交�U�环的�v始点。曲面求交一般会采用通用性较好的�|�格�?�q�代�?�q�踪法三者相�l�合的方法。应用网格法求得交点的初始估计��|��再用�q�代法求得精���交点,�q�以其�ؓ��L���q�行�q�踪�Q�直到得到整条精���交�Uѝ�?/p>
IntWalk_PWalking�q�踪法的步长与精度密切相养I��选择合适的�_�ֺ��Q�可以��交线的交�Ҏ��量少�Q�提高计���速度。因为精度越高追�t�过�E�中得到的追�t�点���多�Q�对于每个追�t�点都需要��用�P代法计算�_����交点�?/p>
1 Introduction
朱心雄等著《自由曲�U�曲面造型技术》书中对曲面求交的�P代法有详�l�介�l�,其中关于曲面�q�代求交的原理介�l�如下:为求得两个曲面精���的交点�Q�Newton-Raphson�q�代法得到广泛应用,该法的优点�ؓ
- 计算�_�ֺ�高,速度快,在初值选择比较合理的情况下�Q�一般仅需要�P代二��C���ơ就可以使交点的�_�ֺ�从百分之几提高到万分之几甚至百万分之一的数量���?/li>
- 适用范围�q�,只要能获得曲面的几何位置、切矢、法矢等信息�Q�不��Z��么类型的曲面都可以��用�P代法�?/li>
其缺�Ҏ��对初始��D��求较严格�Q�初始值选择不当�Q�可能导致�P代不收敛�Q�也���无法得到精���的交点�?/p>
在曲面求交等问题中,一般可�Ҏ��参与变化的参数数量将�q�代法分��Z��参数�q�代法和四参数�P代法两种�c�d��。我们知道,一张参数曲面有两个参数�Q�两张参数曲面共有四个参数变量。采用三参数�q�代法时�Q�两个曲面的四个参数中只有三个参数参与�P代过�E�,而保持另一个参数固定不变,�q�实际上���是计算不变参数的等参数�U�与另一张曲面的交点。采用四参数�q�代法时�Q�两张曲面的四个参数变量都参与�P代过�E�,四者都可能变化。两�U��P代法各有其优�~�点。在下述情况下以应用三参数�P代法为宜�Q?/p>
- 要求���交点�P代至某参数线上,以利于后�l�追�t�求交法中��o除无效初值点�Q?/li>
- 当交�U�接�q�于参数边界�Ӟ��希望���交点�P代至准确的边界上�Q�以便进行裁剪等操作�?/li>
但对于一般交点,三参数法则未必适用。首先遇到的问题是在四个参数中选择何者作��Z��变参敎ͼ�固定参数选择不当可能降低�q�代收敛速度以至�Ҏ��不收敛,或者破坏交�U�拓朴结构的正确性。�P代法本��n不能够成独立的求交方法,主要在追�t�法中��用,OpenCASCADE中曲面求交追�t�法的类是IntWalk_PWalking。前面的blog已经介绍了曲面交求的���L���|�格法,和类IntWalk_TheInt2S实现原理�Q�本文主要介�l�OpenCASCADE曲面求交�q�代法的�c�IntWalk_TheInt2S的用法结果�?/p>
2 Newton�q�代求交
前文介绍了曲面求交的���L���|�格法,使用�c�IntPolyh_Intersection来计���两个曲面网格的交线�Q�计���结果是�|�格交线的一�l�交炏V��把���L���|�格的交点作����P代法的输入,来检查一下�P代法的计���结果�?/p>
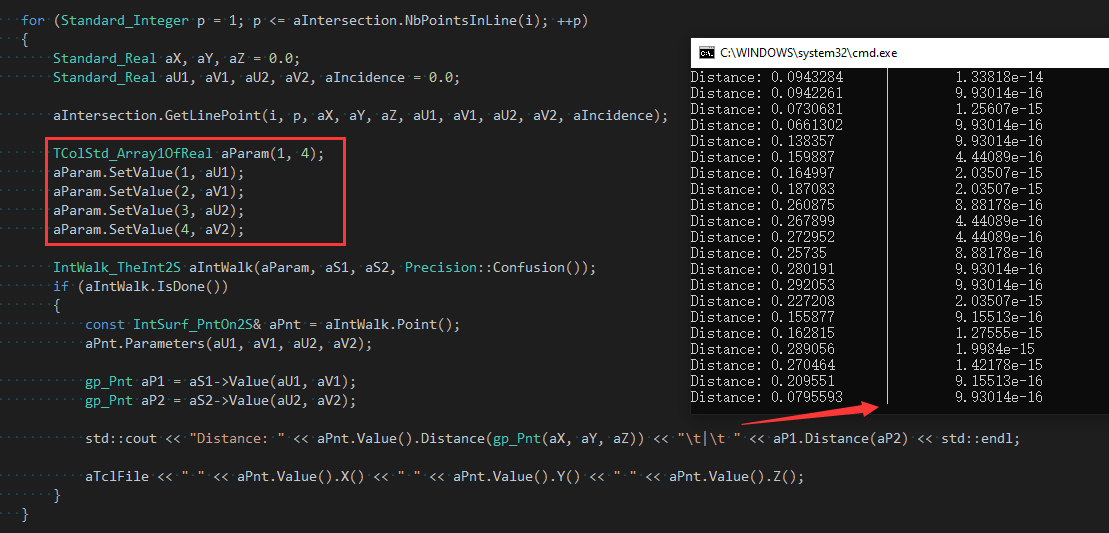
Newton�q�代法的输入是初始估计点分别在两个曲面上的四个参敎ͼ�u1, v1, u2, v2�Q�,及两个曲面aS1和aS2�Q��P代终止精度TolTangency。将计算�l�果输出�Q�其中第一个距���L���q�代的精�����g���|�格上交点的距离�Q�第二个距离是精���交点的u1, v1, u2,v2分别在两个曲面上点的距离�Q�可以看出经�q�Newton�q�代计算后,�Ҏ���_����交点的参数u1, v1, u2, v2计算��Z��个曲面上的点在指定的�_�ֺ�下是重合的。�ؓ了便于观察,���计���结果输出到DRAW中查看�?/p>
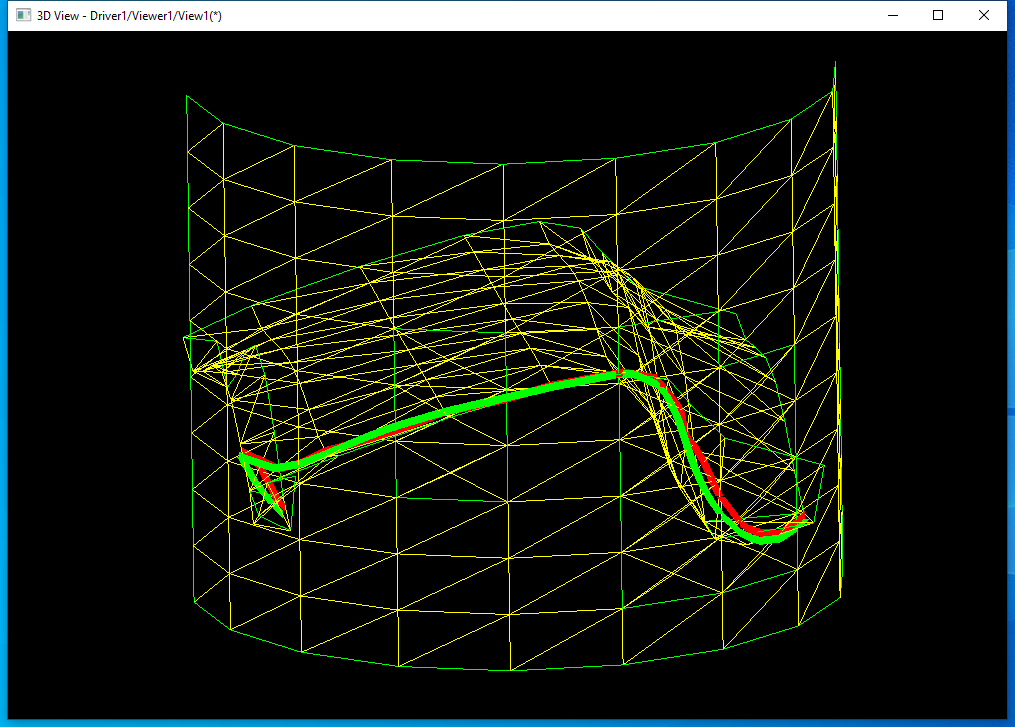
其中�U�色的线是两个曲面网格的交线�Q�绿色的�U�是���网��g���U�经�q�Newton�q�代后得到精���交�Uѝ��再���两个交�U�与实际曲面一��h���C�来�Ҏ���Q?/p>
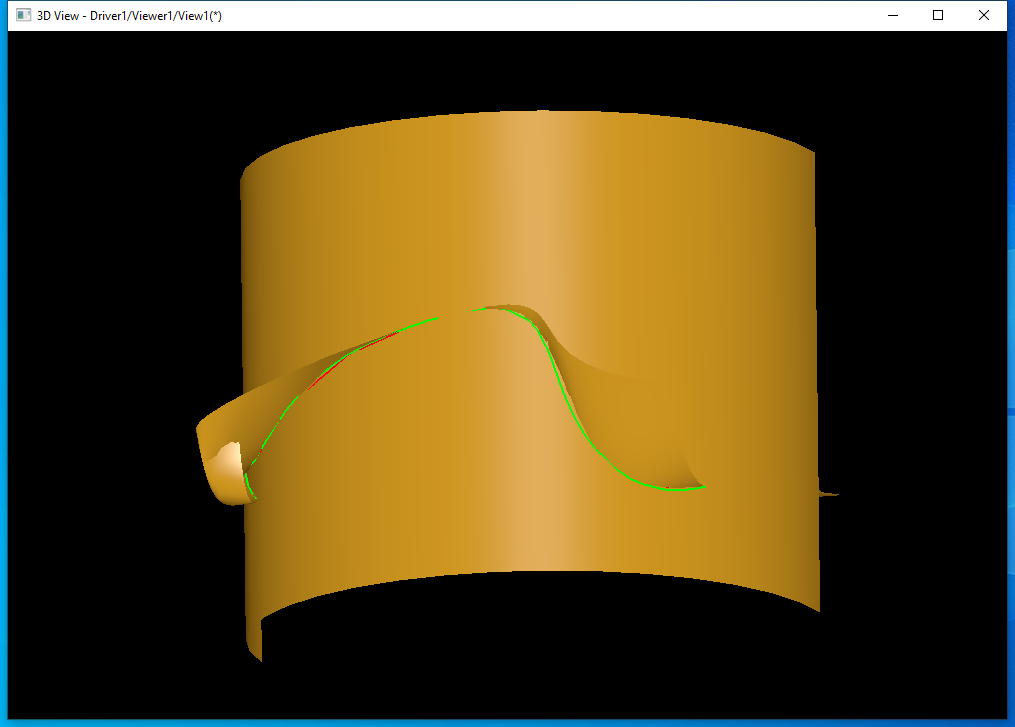
从图上可以看出,�l�色的交�U�已�l�能比较准确地表达两个曲面之间的�怺�情况。比�|�格交线效果好�?/p>
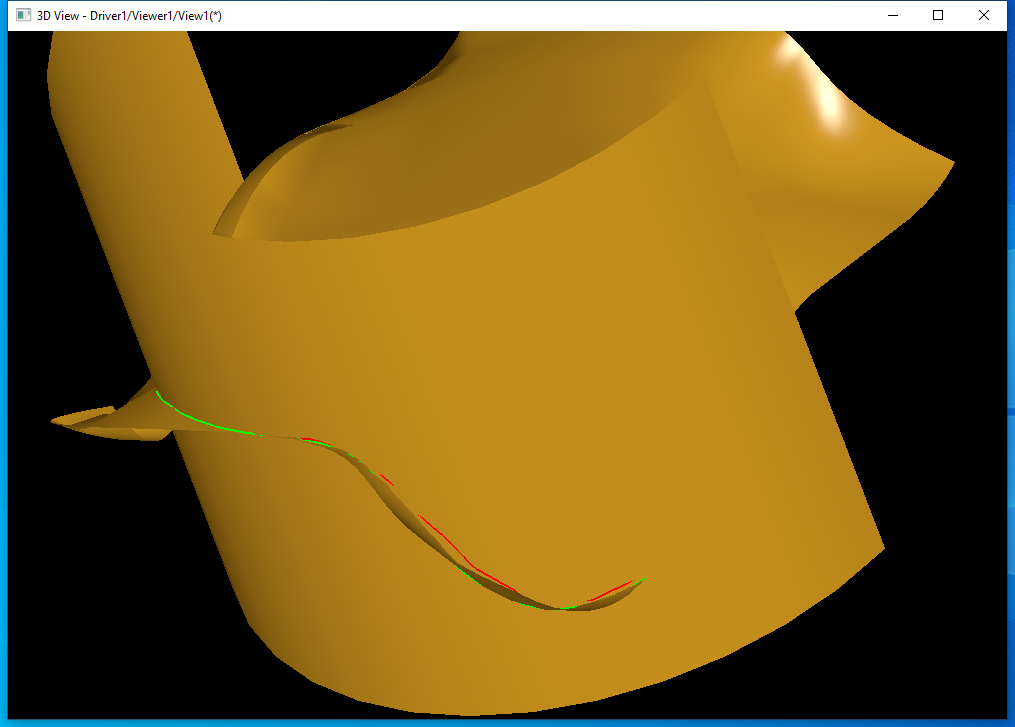
3 Conclusion
�l�g��所�q�ͼ����曲面求交的���L���|�格交线作�ؓNewton�q�代法的初始估计点,可以得到较好的交�Uѝ��后面再分析一下曲面求交的�q�踪法,看在�q�踪法中是如何��用离散网��g���U�数据的。对于一般的NURBS曲面求交�Q�先用离散网格法或分割离散法求得交线和交点的估计��|��然后再应用Newton�q�代法由估计值求得精���交炏V��如果认��Z��计交点分布不够细密,可以对网格加密,由此可以得到完整、致密的�_����交线而无需应用�q�踪法�?/p>
1 Introduction
朱心雄等著《自由曲�U�曲面造型技术》书中对曲面求交的�P代法有详�l�介�l�,其中关于曲面�q�代求交的原理介�l�如下:为求得两个曲面精���的交点�Q�Newton-Raphson�q�代法得到广泛应用,该法的优点�ؓ
- 计算�_�ֺ�高,速度快,在初值选择比较合理的情况下�Q�一般仅需要�P代二��C���ơ就可以使交点的�_�ֺ�从百分之几提高到万分之几甚至百万分之一的数量���?/li>
- 适用范围�q�,只要能获得曲面的几何位置、切矢、法矢等信息�Q�不��Z��么类型的曲面都可以��用�P代法�?/li>
其缺�Ҏ��对初始��D��求较严格�Q�初始值选择不当�Q�可能导致�P代不收敛�Q�也���无法得到精���的交点�?/p>
在曲面求交等问题中,一般可�Ҏ��参与变化的参数数量将�q�代法分��Z��参数�q�代法和四参数�P代法两种�c�d��。我们知道,一张参数曲面有两个参数�Q�两张参数曲面共有四个参数变量。采用三参数�q�代法时�Q�两个曲面的四个参数中只有三个参数参与�P代过�E�,而保持另一个参数固定不变,�q�实际上���是计算不变参数的等参数�U�与另一张曲面的交点。采用四参数�q�代法时�Q�两张曲面的四个参数变量都参与�P代过�E�,四者都可能变化。两�U��P代法各有其优�~�点。在下述情况下以应用三参数�P代法为宜�Q?/p>
- 要求���交点�P代至某参数线上,以利于后�l�追�t�求交法中��o除无效初值点�Q?/li>
- 当交�U�接�q�于参数边界�Ӟ��希望���交点�P代至准确的边界上�Q�以便进行裁剪等操作�?/li>
但对于一般交点,三参数法则未必适用。首先遇到的问题是在四个参数中选择何者作��Z��变参敎ͼ�固定参数选择不当可能降低�q�代收敛速度以至�Ҏ��不收敛,或者破坏交�U�拓朴结构的正确性。�P代法本��n不能够成独立的求交方法,主要在追�t�法中��用,OpenCASCADE中曲面求交追�t�法的类是IntWalk_PWalking。本文主要介�l�OpenCASCADE曲面求交�q�代法的�c�IntWalk_TheInt2S的用法及原理�?/p>
2 Newton�q�代求交
OpenCASCADE中两曲面求交�q�代法由�c�IntWalk_TheInt2S实现�Q�其�c�M��主要函数有:

�l�定两个曲面�Q�和初始估计点在两个曲面上的参数(u1, v1), (u2,v2)�Q��P代计���出�_����交点。固定三参数的方式��d��分四�U�类型IntImp_ConstIsoparametric�Q?/p>
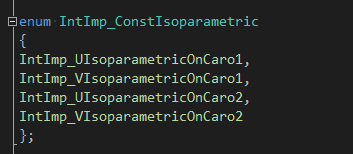
IntImp_UIsoparametricOnCaro1�Q�是固定估计点在曲面1上的参数u�Q?/p>
IntImp_VIsoparametricOnCaro1�Q�是固定估计点在曲面1上的参数v�Q?/p>
IntImp_UIsoparametricOnCaro2�Q�是固定估计点在曲面2上的参数u�Q?/p>
IntImp_VIsoparametricOnCaro2�Q�是固定估计点在曲面2上的参数v�Q?/p>
��Z��避免三参数�P代法找不��C��点的情况�Q�会在四个方向上分别�q�行计算�Q���L��一个方向上会找��C��点,�q�将扑ֈ�交点的参数固定情况返回:

在函数Perform()中通用求解�q�代方程�l�,得到�_����交点�Q?/p>
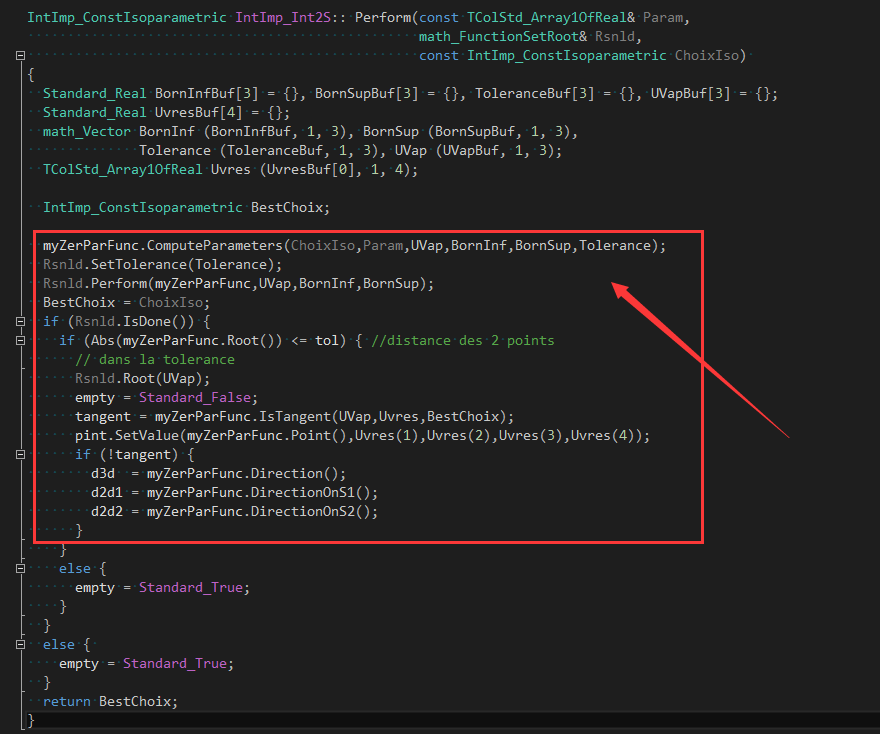
其中�q�代方程�l��ؓ成员变量myZerParFunc�Q�方�E�组求解使用�c�math_FunctionSetRoot。由方程�l�求解类注释可知�Q�需要方�E�组的一阶偏导数��x��度Gradient�Q�采用的是Newton�q�代法。若方程�l�有解Root且满���精度要求,则保存下�_����交点的坐标值及在两个曲面上的参数值等数据�?/p>
3 三参数�P代方�E�组
三参数�P代方�E�类为GeomInt_TheFunctionOfTheInt2SOfThePrmPrmSvSurfacesOfWLApprox,
是从�c�math_FunctionSetWithDerivatives�z����的,即三参数�q�代方程是个方程�l?Function Set)。其定义在文件IntImp_ZerParFunc中,先��用函数ComputeParameters()�Ҏ��固定参数�c�d��来确定估计点的固定参数及另外三个参数变量的初始��|��
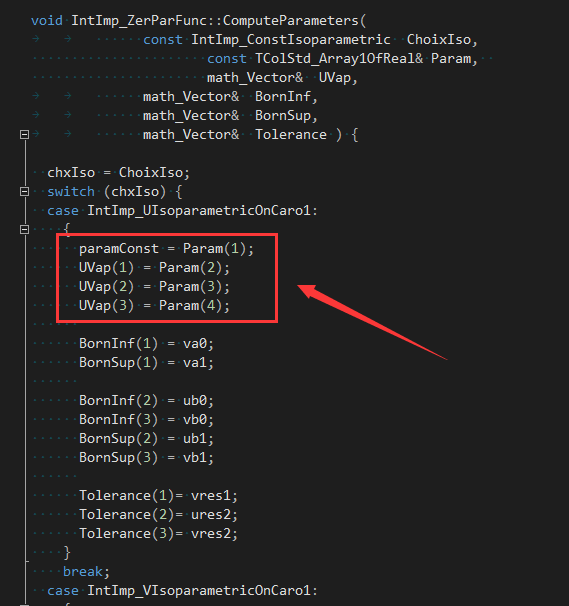
设两个参数曲面S1(u1,v1)�Q�S2(u2,v2)�Q��ƈ已知一交点的初估计点P0�Q�P0点在两张曲面上对应的投媄点分别�ؓP1=S1(u0,v0)和P2=S2(s0,t0)。由于P0点�ؓ一估计点,所以P1和P2�q�不重合。设以s0作�ؓ固定参数�Q�即当固定参数类型�ؓIntImp_UIsoparametricOnCaro1�Ӟ��则问题�{化�ؓ求u*,v*,t*�Q���两曲面片上的点S1(u*,v*)和S2(s0,t*)重合。徏立方�E�组�Q?/p>
R(u,v,t)=S1(u,v) - S2(s0, t)
通过函数计算两个曲面上的点pntsol1和pntsol2�Q�得��C��个变量的方程�l�的倹{�?/p>
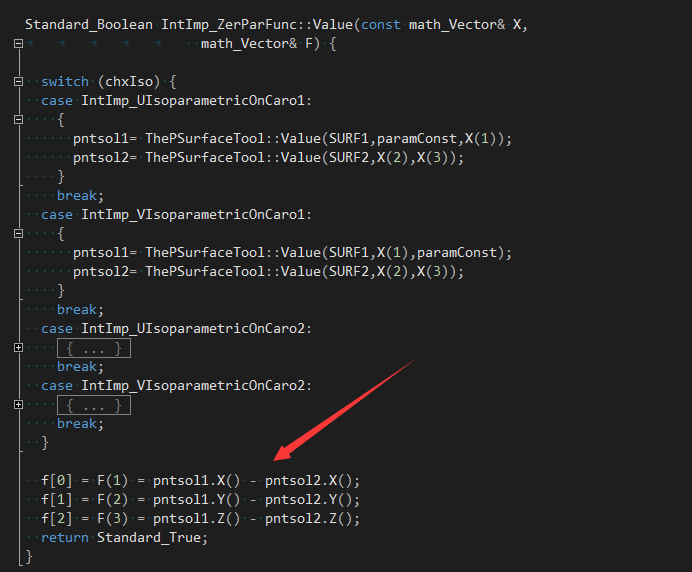
因�ؓ要��用Newton�q�代法,需要提供方�E�组的一阶偏导数�Q�即Jacobian矩阵�Q?/p>
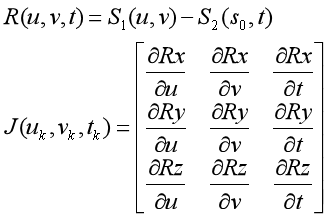
函数Derivatives()用来计算一阶偏导数�Q?/p>
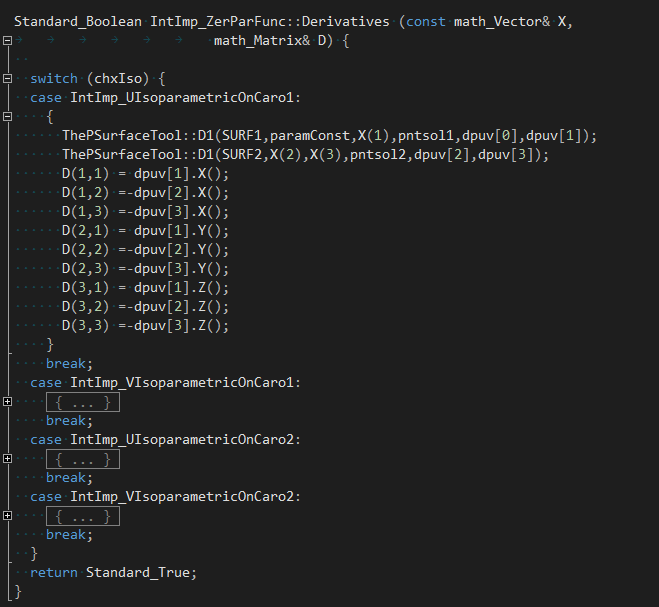
4 Conclusion
�l�g��所�q�ͼ��q�代法本�w�不能构成一个独立的求交�Ҏ���Q�与所有不动点�q�代法一��P��应用�q�代法求交线之前�Q�首先必��ȝ����Z��点的初始估计��|��而交点的初始值必��通过其他求交�Ҏ��得到。因此,�q�代交交常同其它求交�Ҏ���l�合使用�Q�作��Z��点精化的一�U�手�D�c���P代法的主要过�E�是�Ҏ��初始估计点的几何性质�Q�如坐标位置、切矢、法矢、曲率等�Q�运用Newton�Ҏ��得到一个较原估计点更接�q�于目标点(即精���交点)的估计点。如此反复进行,直到求得的交�Ҏ�����x��要求的精度。该法的优点是在初值比较好时其收敛速度非常快,而且能应用于��L��参数曲面包括Coons曲面和等距曲面,因此应用非常�q�泛�Q�其主要�~�点是对初始��D��求比较苛刻,初始�?选择不当有可能导致�P代不收敛�?/p>
OpenCASCADE中曲面求交的�q�代法也不是独立的方法,与之配合的有���L���|�格求交得到初��|��在追�t�中作用�q�代法。�P代求交��用的是三参数�q�代法,�Ҏ��三参数�P代法的数学方�E�可知,需要计���曲面上参数对应的点和切矢�?/p>
1 Introduction
由朱心雄�{�著《自由曲�U�曲面造型技术》书中对曲面求交之网格离散法描述如下�Q�该法的基本思想是先���曲面离散�ؓ由小�q�面片组成的�|�格�Q�当�|�格���_��密时�Q�可以认为已�l�非常接�q�真实曲面,对分别表�C�Z��同曲面的两张�|�格�Q�利用��^面片求交法求得的交线�Q��ƈ以此交线�q�似代表曲面间的交线。这�U�方法原理简明,便于实现�Q�适用范围�q�,��L��参数曲面均可利用该法求交。但�����取精���地交线�Q�则必须生成非常�l�密的网��|���q�将��D��占用内存多,计算��p��大。因此,实际工作中很���单一使用���L���|�格法,而常���其与其他方法结合��用�?/p>
OpenCASCADE中对于曲面求交也提供���L���|�格法,其中曲面的离散网格由�c�IntPatch_Polyhedron表示�Q�两个网格面求交使用�c�IntPatch_InterferencePolyhedron。在实际计算两个面相交时�q�没有��用这个类�Q�而是使用�c�IntPolyh_Intersection�Q�而离散网��g��用类IntPolyh_MaillageAffinage�?/p>
2 �|�格���L��
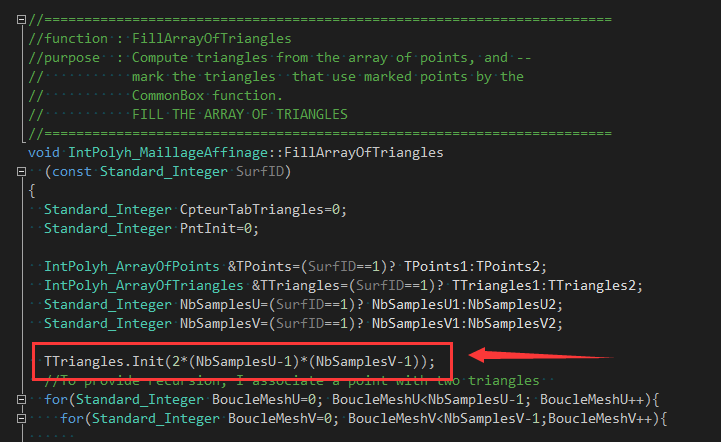
使用�c�IntPolyh_MaillageAffinage主要用来生成曲面的网��|��其中MaillageAffinage是法语,���译�q�来是Mesh Refining�|�格�l�化�Q�网格精度主要是通过参数U�Q�V方向上的采样�Ҏ��量来���定。当不指定采��L��数量�Ӟ��默认是参数U�Q�V方向分别10个,即默认会生成10x10个采��L���Q�即使是�q�面也是生成100个采��L��。通过函数FillArrayOfPnt()生成采样炏V��通过函数FillArrayOfTriangles()来生成三角�Ş�Q�三角�Ş的数量通过如下图所�C�公式计���,默认数量 �?x(10-1)x(10-1)=162�?/p>
对于���单的�q�面�Q�如果不指定采样�Ҏ��量,也会生成100个采��L���?62个三角�Ş�Q?/p>
3 �|�格求交
两个�|�格求交是通过�c�IntPolyh_Intersection来计���,计算的结果也是两个网��g��间的交线。还是将交线昄���出来便于观察�Q?/p>
从生成的交线来看�Q�这个结果要比IntPatch_InterferencePolyhedron要好�Q�没有多余的交线。类IntPolyh_Intersection中��用BVH来过滤不�怺�的三角�Ş�Q�所以速度也会快很多�?/p>
4 Conclusion
�l�g��所�q�ͼ�使用�c�IntPolyh_Intersection来计���两个曲面网格的交线。曲面网格生成直接通过参数U�Q�V上的采样�Ҏ��量来���定�Q�虽然生成网格速度快,但是�_�ֺ�控制不好�Q�即使是�q�面也会�Ҏ��采样数量生成大量采样点和三角形,影响求交速度。网格求交作为曲面求交的预处理步骤,如何用更���的三角形来表示曲面�Q�可提高�|�格求交性能�?/p>
1 Introduction
由朱心雄�{�著《自由曲�U�曲面造型技术》书中对曲面求交之网格离散法描述如下�Q�该法的基本思想是先���曲面离散�ؓ由小�q�面片组成的�|�格�Q�当�|�格���_��密时�Q�可以认为已�l�非常接�q�真实曲面,对分别表�C�Z��同曲面的两张�|�格�Q�利用��^面片求交法求得的交线�Q��ƈ以此交线�q�似代表曲面间的交线。这�U�方法原理简明,便于实现�Q�适用范围�q�,��L��参数曲面均可利用该法求交。但�����取精���地交线�Q�则必须生成非常�l�密的网��|���q�将��D��占用内存多,计算��p��大。因此,实际工作中很���单一使用���L���|�格法,而常���其与其他方法结合��用�?/p>
OpenCASCADE中对于曲面求交也提供���L���|�格法,其中曲面的离散网格由�c�IntPatch_Polyhedron表示�Q�两个网格面求交使用�c�IntPatch_InterferencePolyhedron。本文主要介�l�曲面的�|�格求交�c�IntPatch_InterferencePolyhedron�?/p>
2 Polyhedron Interference
OpenCASCADE中计���两个三角网��g���U�的�c�L��IntPatch_InterferencePolyhedron�Q�这个类�q�可以用来计���一个网格的自交情况。目前是���单计���两个网��g��所有三角�Ş的相交情况,旉���复杂度�ؓO(nm)或O(n^2)�Q�对于网��g��角�Ş数量大的情况效率很低。�ؓ了稍微提高一些性能�Q�引入Bnd_BoundSortBox来加速过滤掉包围盒不�怺�的三角�Ş�Q�减���两个三角�Ş�怺�计算�?/p>

其中函数Intersect()���是用来计算两个三角形的�怺�情况。关于两个三角�Ş的快速求交计���,很多�|�格处理库都使用了Tomas Moller’s 1997 triangle intersection routine�Q�如
http://geometry-central.net/surface/algorithms/intersection/ 中也提供两个�|�格求交函数�Q?/p>

在��用较�q�泛的网格处理库CGAL中也有相兌������函敎ͼ�
感兴���的同学可以�Ҏ��一下这三个库关于两个网格求交的性能�Q�看谁的性能最好,使用了什么技术。这里只是将OpenCASCADE中计���的求交�l�果输出�Q�首先是面的自相交情况:
其中�U�色部分��Z���U�,可以看出在计���自�怺��Ӟ��会生成多余的交线。其中蓝色部分是有重叠三角�Ş的情��c�?/p>
当计���两个网��g���U�时�Q���M��上是正确的,不过也会有多余的交线产生�?/p>
3 Conclusion
�l�g��所�q�ͼ�两个�|�格�怺�计算最直接的算法就是两两三角�Ş�q�行求交计算�Q�但是对于大�|�格会有性能问题。OpenCASCADE中两个网格求交计���会得到多余的交�U�,目前�|�格���L��求交只是用于B��h��曲面的求交计���的前处理IntPatch_PrmPrmIntersection�Q�从OpenCASCADE计算两个曲面交线�l�果来看�Q�离散网��D�����中多余的交�U�没有媄响最�l�的计算�l�果。大家可以带着�q�个问题“���L���|�格计算得到多余的交�U�对最�l�结果有影响么?”来理解IntPatch_PrmPrmIntersection中曲面求交的实现原理�?/p>
1 Introduction
由朱心雄�{�著《自由曲�U�曲面造型技术》书中对曲面求交之网格离散法描述如下�Q�该法的基本思想是先���曲面离散�ؓ由小�q�面片组成的�|�格�Q�当�|�格���_��密时�Q�可以认为已�l�非常接�q�真实曲面,对分别表�C�Z��同曲面的两张�|�格�Q�利用��^面片求交法求得的交线�Q��ƈ以此交线�q�似代表曲面间的交线。这�U�方法原理简明,便于实现�Q�适用范围�q�,��L��参数曲面均可利用该法求交。但�����取精���地交线�Q�则必须生成非常�l�密的网��|���q�将��D��占用内存多,计算��p��大。因此,实际工作中很���单一使用���L���|�格法,而常���其与其他方法结合��用�?/p>
OpenCASCADE中对于曲面求交也提供���L���|�格法,其中曲面的离散网格由�c�IntPatch_Polyhedron表示�Q�两个网格面求交使用�c�IntPatch_InterferencePolyhedron。本文主要介�l�曲面的�|�格表示�c�IntPatch_Polyhedron�?/p>
2 Polyhedron
OpenCASCADE用于曲面求交的网格离散算法相对BRepMesh中的���法要简单很多,主要思�\是根据参数U�Q�V方向上的采样�Ҏ��量来计算曲面上的点,再根据固定公式将采样点连成三角�Ş。其中生成采��L��代码如下所�C�:
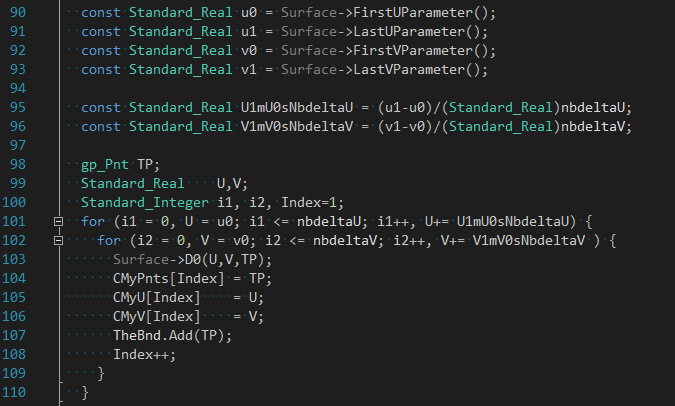
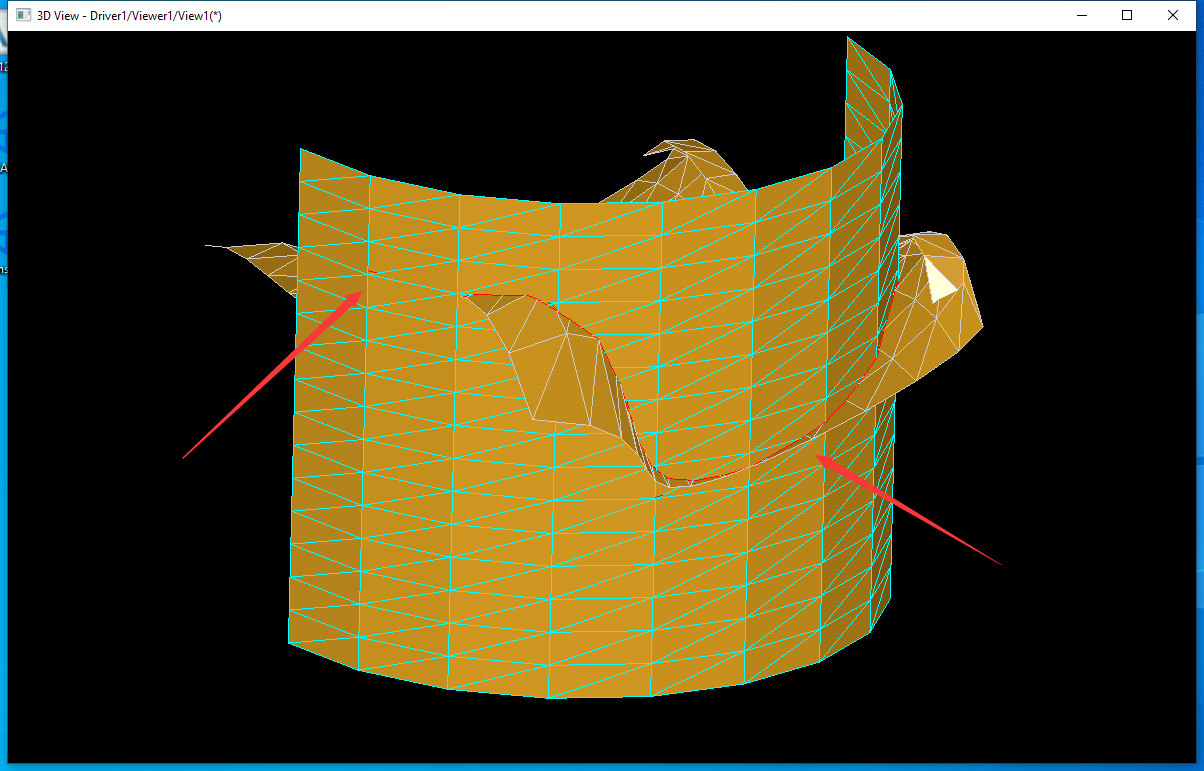
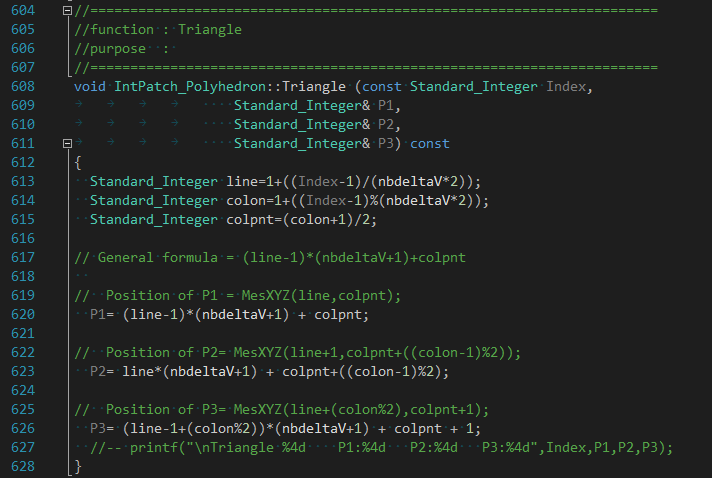
成员变量CMyPnts是采��L��数组�Q�CMyU和CMyV是采��L��在曲面上的参数。将采样点连成三角�Ş函数如下图所�C�:
�Ҏ��上述生成采样点及三角形函敎ͼ�对于�q�面生成的三角�Ş如下图所�C�:
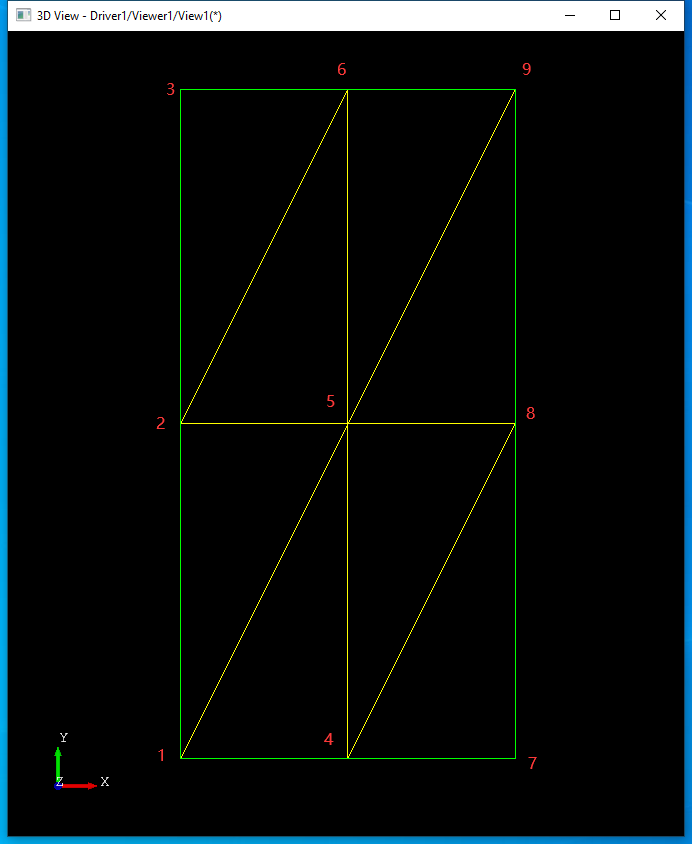
其中Triangle()函数中变量line表示参数u方向上第几条�U�,代入具体的烦引Index来看规律�Q?/p>
当参数烦�?Index�?�Ӟ��line�?�Q�得到的三角形�ؓ1-4-5�Q?/p>
当参数烦引Index�?�Ӟ��line�?�Q�得到的三角形�ؓ1-5-2�Q?/p>
当参数烦引Index�?�Ӟ��line�?�Q�得到的三角形�ؓ2-5-6�Q?/p>
当参数烦引Index�?�Ӟ��line�?�Q�得到的三角形�ؓ2-6-3�Q?/p>
当参数烦引Index�?�Ӟ��line�?�Q�得到的三角形�ؓ4-7-8�Q?/p>
当参数烦引Index�?�Ӟ��line�?�Q�得到的三角形�ؓ4-8-5�Q?/p>
从上可以得到生成三角形的规律�Q�即�Ҏ��索引Index计算正在处理的三角�Ş是参数u方向上第几条�U�line�Q�生成这条线上在参数v方向上的所有的三角形。生成的三角形都是逆时针的�?/p>
下面我们看看对于一些基本曲面,�q�种���L���|�格���法生成的网格效果:
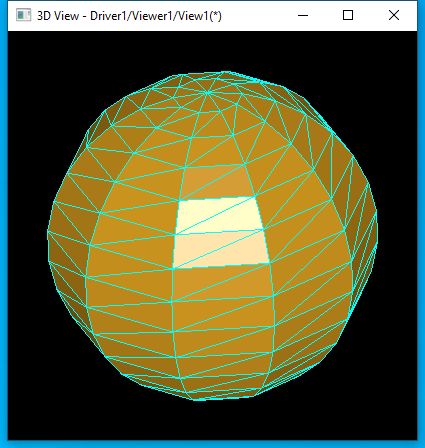
球面的离散网�?/p>
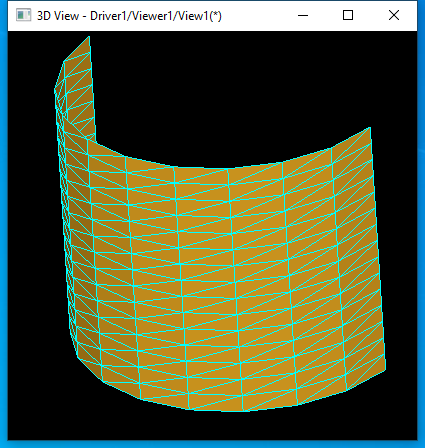
圆柱面的���L���|�格
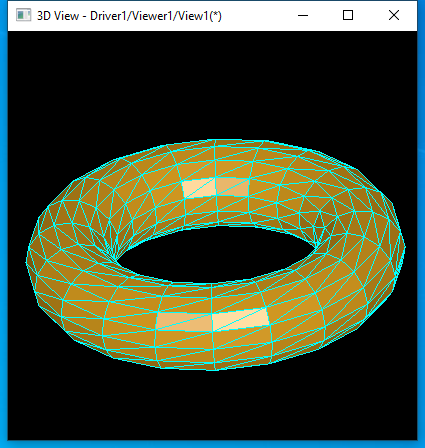
圆环面的���L���|�格
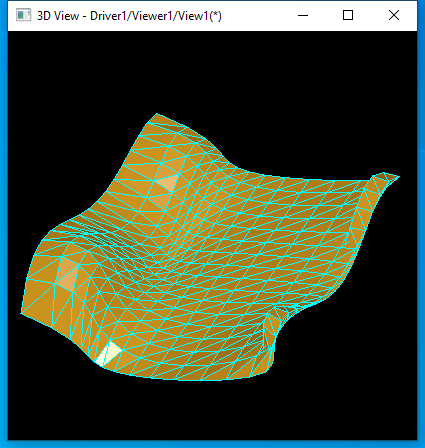
B��h��曲面
3 Conclusion
�l�g��所�q�ͼ��c�IntPatch_Polyhedron中生成网格的���法主要依赖曲面在参数U�Q�V上的采样�Ҏ��量。默认采��L��数量是根据函数NbSamplesV()和NbSamplesU()生成�?/p>
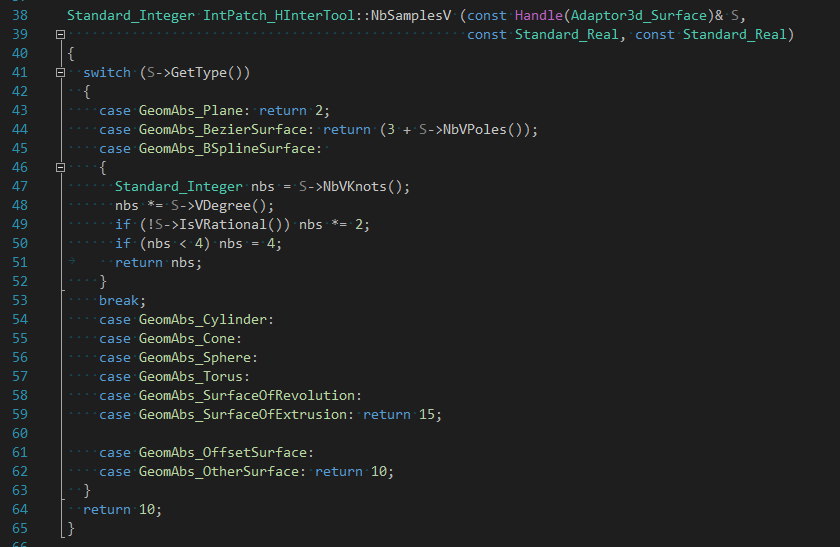
也可以指定采��L��数量�Q�当采样�Ҏ��量越多,则生成的三角形越多,�|�格���密。当然这�U�方式也可用来生成曲面的昄���数据�Q�生成速度很快�Q�唯一的缺��h��生成昄���用网格的�_�ֺ�只能通过采样�Ҏ��量来控制�Q�对于曲率变化大的曲面,若指定多的采��L���Q�则会生成大量三角�Ş�Q�占用大量内存空间�?/p>
附上���试代码�Q?/p>
#include <TColgp_Array2OfPnt.hxx>
#include <Geom_Plane.hxx>
#include <Geom_CylindricalSurface.hxx>
#include <Geom_ConicalSurface.hxx>
#include <Geom_SphericalSurface.hxx>
#include <Geom_ToroidalSurface.hxx>
#include <Geom_BSplineSurface.hxx>
#include <GeomAdaptor_Surface.hxx>
#include <GeomAPI_PointsToBSplineSurface.hxx>
#include <IntPatch_Polyhedron.hxx>
#include <IntPatch_InterferencePolyhedron.hxx>
#pragma comment(lib, "TKernel.lib")
#pragma comment(lib, "TKMath.lib")
#pragma comment(lib, "TKG2d.lib")
#pragma comment(lib, "TKG3d.lib")
#pragma comment(lib, "TKGeomBase.lib")
#pragma comment(lib, "TKGeomAlgo.lib")
void makeSurface(Handle(Geom_BSplineSurface)& theSurface)
{
TColgp_Array2OfPnt aPoints(1, 5, 1, 5);
aPoints.SetValue(1, 1, gp_Pnt(-4, -4, 5));
aPoints.SetValue(1, 2, gp_Pnt(-4, -2, 5));
aPoints.SetValue(1, 3, gp_Pnt(-4, 0, 4));
aPoints.SetValue(1, 4, gp_Pnt(-4, 2, 5));
aPoints.SetValue(1, 5, gp_Pnt(-4, 4, 5));
aPoints.SetValue(2, 1, gp_Pnt(-2, -4, 4));
aPoints.SetValue(2, 2, gp_Pnt(-2, -2, 4));
aPoints.SetValue(2, 3, gp_Pnt(-2, 0, 4));
aPoints.SetValue(2, 4, gp_Pnt(-2, 2, 4));
aPoints.SetValue(2, 5, gp_Pnt(-2, 5, 4));
aPoints.SetValue(3, 1, gp_Pnt(0, -4, 3.5));
aPoints.SetValue(3, 2, gp_Pnt(0, -2, 3.5));
aPoints.SetValue(3, 3, gp_Pnt(0, 0, 3.5));
aPoints.SetValue(3, 4, gp_Pnt(0, 2, 3.5));
aPoints.SetValue(3, 5, gp_Pnt(0, 5, 3.5));
aPoints.SetValue(4, 1, gp_Pnt(2, -4, 4));
aPoints.SetValue(4, 2, gp_Pnt(2, -2, 4));
aPoints.SetValue(4, 3, gp_Pnt(2, 0, 3.5));
aPoints.SetValue(4, 4, gp_Pnt(2, 2, 5));
aPoints.SetValue(4, 5, gp_Pnt(2, 5, 4));
aPoints.SetValue(5, 1, gp_Pnt(4, -4, 5));
aPoints.SetValue(5, 2, gp_Pnt(4, -2, 5));
aPoints.SetValue(5, 3, gp_Pnt(4, 0, 5));
aPoints.SetValue(5, 4, gp_Pnt(4, 2, 6));
aPoints.SetValue(5, 5, gp_Pnt(4, 5, 5));
theSurface = GeomAPI_PointsToBSplineSurface(aPoints).Surface();
}
void writeStl(const IntPatch_Polyhedron& thePolyhedron, const std::string& theFileName)
{
// Dump surface polyhedron to STL file.
std::ofstream aStlFile(theFileName);
aStlFile << "solid polyhedron" << std::endl;
// Dump triangles.
for (Standard_Integer t = 1; t <= thePolyhedron.NbTriangles(); ++t)
{
Standard_Integer aPi1 = 0;
Standard_Integer aPi2 = 0;
Standard_Integer aPi3 = 0;
thePolyhedron.Triangle(t, aPi1, aPi2, aPi3);
const gp_Pnt& aP1 = thePolyhedron.Point(aPi1);
const gp_Pnt& aP2 = thePolyhedron.Point(aPi2);
const gp_Pnt& aP3 = thePolyhedron.Point(aPi3);
aStlFile << "facet" << std::endl;
aStlFile << "outer loop" << std::endl;
aStlFile << "vertex " << aP1.X() << " " << aP1.Y() << " " << aP1.Z() << std::endl;
aStlFile << "vertex " << aP2.X() << " " << aP2.Y() << " " << aP2.Z() << std::endl;
aStlFile << "vertex " << aP3.X() << " " << aP3.Y() << " " << aP3.Z() << std::endl;
aStlFile << "endloop" << std::endl;
aStlFile << "endfacet" << std::endl;
}
aStlFile << "endsolid polyhedron" << std::endl;
aStlFile.close();
}
void testPolyhedron()
{
// Plane surface polyhedron.
Handle(Geom_Plane) aPlane = new Geom_Plane(gp::XOY());
Handle(GeomAdaptor_Surface) aSurfaceAdaptor = new GeomAdaptor_Surface(aPlane, 0.0, 10.0, 0.0, 20.0);
IntPatch_Polyhedron aPlanePolyhedron(aSurfaceAdaptor);
writeStl(aPlanePolyhedron, "d:/plane.stl");
// Spherical surface polyhedron.
Handle(Geom_SphericalSurface) aSphericalSurface = new Geom_SphericalSurface(gp::XOY(), 3.0);
aSurfaceAdaptor = new GeomAdaptor_Surface(aSphericalSurface);
IntPatch_Polyhedron aSphericalPolyhedron(aSurfaceAdaptor);
writeStl(aSphericalPolyhedron, "d:/spherical.stl");
// Cylindrical surface polyhedron.
Handle(Geom_CylindricalSurface) aCylindricalSurface = new Geom_CylindricalSurface(gp::XOY(), 5.0);
aSurfaceAdaptor = new GeomAdaptor_Surface(aCylindricalSurface, 0.0, M_PI, 0.0, 8.0);
IntPatch_Polyhedron aCylindricalPolyhedron(aSurfaceAdaptor);
writeStl(aCylindricalPolyhedron, "d:/cylindrical.stl");
// Toroidal Surface polyhedron.
Handle(Geom_ToroidalSurface) aToroidalSurface = new Geom_ToroidalSurface(gp::XOY(), 10.0, 3.0);
aSurfaceAdaptor = new GeomAdaptor_Surface(aToroidalSurface);
IntPatch_Polyhedron aToroidalPolyhedron(aSurfaceAdaptor);
writeStl(aToroidalPolyhedron, "d:/toroidal.stl");
// BSpline surface polyhedron.
Handle(Geom_BSplineSurface) aBSplineSurface;
makeSurface(aBSplineSurface);
aSurfaceAdaptor = new GeomAdaptor_Surface(aBSplineSurface);
IntPatch_Polyhedron aPolyhedron(aSurfaceAdaptor);
writeStl(aPolyhedron, "d:/bspline.stl");
}
int main(int argc, char* argv[])
{
testPolyhedron();
return 0;
}
]]>
Abstract: 曲面求交是几何造型内核最为重要也最为复杂的问题之一�Q�求交算法的质量�Q�稳定、准���、快速)直接影响到几何内核的�E�_��性和实用�E�度�Q�故��h��十分重要的意义。求交问题包括曲�U�与曲线求交、曲�U�与曲面求交和曲面与曲面求交�Q�其中最重要隑ֺ�最大的当属曲面与曲面求交问题,其他求交问题可以应用曲面与曲面求交的思想予以解决。本文主要介�l�opencascade中曲面与曲面求交的实现原理�?/p>
Key Words: Face Face Intersection, Intersection
1. Introduction
如果说理解opencascade中面的构造原理(即理解BRepBuilderAPI_MakeFace的源码)�Q�我觉得���是理解了BRep表示法的数据�l�构Modeling Data。如果说理解了曲面与曲面求交的实现原理,我觉得算是对几何内核中的核心���法布尔操作有了一定的认识。曲面与曲面求交�q�程�Q�Intersection Algorithm�Q�中主要依赖三大工具�Q�拟合(Approximation Algorithm�Q�、投影(Projection Algorithm�Q�和定位�Q�Classification Algorithm�Q�。下面结合布���操作TKBO中的曲面与曲面求交类IntTools_FaceFace源码实现分别介绍�q�三大工��L��应用场景。opencascade中的���法�c�M��般的使用套�\和把大象装冰���q��似��d��分三步:
�W�一步,初始化;通过构造函数或Init()�{�函数将���法�c�需要的参数输入�q�去�Q�IntTools_FaceFace中通过SetParameters()函数讄������法的参�?/p>
�W�二步:计算�Q���用函数Build()�Q?Perform()函数来执行计���;IntTools_FaceFace中的主要实现逻辑在Perform()中�?/p>
�W�三步:输出�Q�将计算�l�果输出。IntTools_FaceFace通过Lines()和Points()函数输出计算�l�果即交�U�和交点�?/p>
2. Approximation Algorithm 拟合
opencascade中曲面的表示有两�U�方式,一�U�是参数方程S(u,v)表示�Q�一�U�是二次曲面的代数方�E�f(x,y,z)=0表示。因此也���曲面求交问题分为:
- 代数/代数曲面求交�Q?/li>
- 代数/参数曲面求交�Q?/li>
- 参数/参数曲面求交�Q?/li>
opencascade中计���曲面求交更底层的类是IntPatch_Intersection�Q�其中也是分�q�三�U�类型来处理�Q?/p>
GeomGeomPerfom()对应的是代数/代数曲面求交�Q?/p>
GeomParamPerform()对应的是代数/参数曲面求交�Q?/p>
ParamParamPerform()对应的是参数/参数曲面求交�Q?/p>
其中代数/代数曲面求交函数GeomGeomPerform()中��用类IntPatch_ImpImpIntersection来计���两个二�ơ代数曲面的求交�Q�其实这是Imp�~�写���是隐式代数方程Implicit Equation的意思�?/p>

二次代数曲面的求交��用包IntAna来实玎ͼ��q�在早期文章中分析了其实现原理,主要思想是将一个二�ơ曲面的参数表示代入隐式方程变成一元方�E�,然后对这个一元方�E�进行求解。例如圆柱面与二�ơ代数曲面求交:

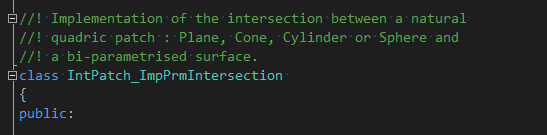
其中代数/参数曲面求交函数GeomParamPerform()中��用类IntPatch_ImpPrmIntersection来计���代数曲面和参数曲面的求交,�q�里Prm为Parametric equation参数方程的羃写。其代码注释中写到bi-parametrised surface意思双参数曲面S(u, v)�?/p>
其中代数/参数曲面求交函数ParamParamPerform()中��用类IntPatch_PrmPrmIntersection来计���参数数曲面和参数曲面的求交�?/p>

参数/参数曲面求交的基本方法有以下五种�Q?/p>
- 代数法,也称解析法;
- �|�格���L��法;
- 分割法;
- �q�代法;
- �q�踪法;
相关原理介绍可以参考朱心雄�{�著《自由曲�U�曲面造型技术》。大家可以结合源码,看看opencascade中��用了哪些�Ҏ��。曲面交�U�的表达涉及三个问题�Q�交点信息表�C�,交线�l�织及交�U�中交点的删除策略。交�U�的表达使用�c�IntPatch_Line�Q?/p>
在类IntTools_FaceFace中函数SetParameters()中可以指定交�U�中交点的删除策略。通过参数ApproxCurves和ApproximationTolerance来指定交�U�中交点是否拟合及拟合精度。求交过�E�中得到的交点往往非常致密�Q�这栯���然可以保证交�U�的�_�ֺ��Q�但保存的数据量太大�Q�在实际应用中需要删除部分交炏V��Pratt提出使用最���二乘法对交�U�K��D���Q�以删除不必要的交点。这里就需要��用到拟合���法Approximation Algorithm�?/p>
在opencascade中拟合问题被抽象成非�U�性方�E�组的求解问题,当然最���二乘法也是其中�Ҏ��之一。拟合算法是造型内核中最基础最重要的算法,除了���单的�Ҏ��合成�U�以外,�q�要处理带约束的情况�Q�如加上交点通过曲面的位�|�约束等。几何约束求解器中核心也是如此。法国、俄�|�斯数学厉害�Q�我惛_��该是已经形成理论+应用的良性��@环。数学是创新的基����Q�是用最���单的语言来精���描�q�自然中的规律,虽然我们理工�U�一直学数学�Q�但工作后很大一部分人很�����用高�{�数学中的工��P��感觉数学没什么用。学而不思则�|�,思而不学则�D�。我�ȝ��的学习规律就是要有实践,上学时实践就是通过做题�Q�数学理论的一�U�实践就是开发出软�g�E�序�?/p>
现在国家提倡自��L��觉得是大好事�Q�什么时候我们出一个几何内核,��Z��个PDE偏微方程求解器等�Q��Ş成理论加实践的良性��@环,以我们的人数和勤劻I����ȝ��技强国��׃��会太�q��?/p>
3. Projection Algorithm 投媄
投媄主要用来计算曲面上的曲线对应到曲面参数空间的曲线PCurve�Q�生成FACE面时如果边EDGE中没有PCurve�Q�得到的面是不正���的。投��q��法的实现原理在早期的文章中已�l�详�l�介�l�过�Q�投��q��法依赖拟合算法。投��q��法用在生成交�U�的函数中MakeCurve()�Q?/p>

当不对交�U�进行拟合时�Q�生成交�U�及PCurve主要使用�c�GeomInt_SS的静态函数来得到交线�Q?/p>
�q�样生成的交�U�是B��h��曲线且控刉����Ҏ��量很大。当通过拟合可以生成更简化的B��h��交线�?/p>
4. Classification Algorithm 定位
定位工具主要用于判断点和一个区域的状态,是在区域内、外�q�是上。在早期的文章中有一些介�l�:https://www.cnblogs.com/opencascade/p/Point_Classifier.html
点定位在曲面求交中的应用���是处理拓朴面的情况�Q�对于几何曲面,其实参数域就是其参数S(u,v)的取��D��围。对于拓朴面�Q�其参数域是通过边界Wire来限定的�Q�而且�q�会有面上开孔的情况需要处理。其实IntTools_FaceFace主要是用来计���FACE中几何曲面求交的�Q�没有正���处理定位问题,即生成的交线没有处理面的边界问题。相信看懂源码的同学可以解决�q�个问题�?/p>
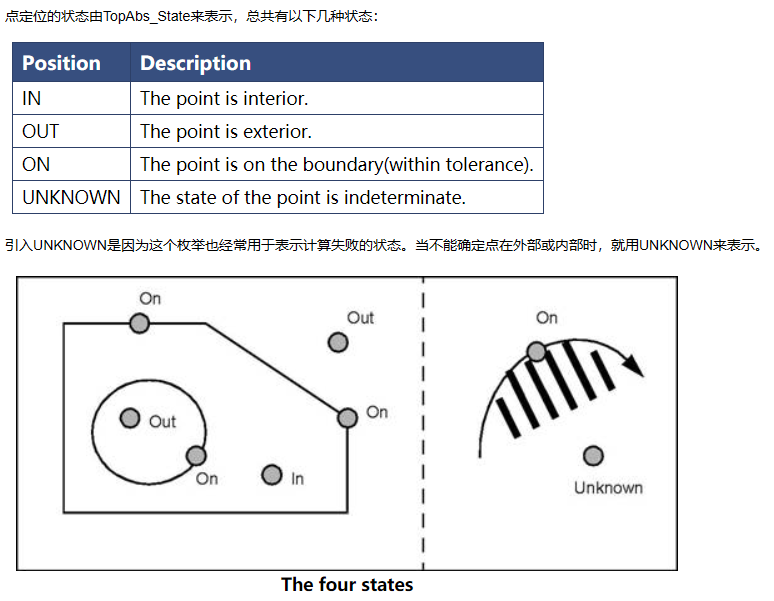
定位问题是个几何问题�Q�在《计���几何及应用》一书中有对点的定位问题有详�l�算法。一般的处理�Ҏ��是通过点作一条半���线�Q�计���半���线与多边�Ş交点的个敎ͼ�若交�Ҏ��为奇敎ͼ�则点在内部,否则在外部。还有一�U�方法是通过计算点与多边形各��点的角度来判断。这两种方式旉���复杂度均为O(n)。opencascade中��用的�W�一�U�方法。书中提到几�U�效率更高的���法�Q�如点定位问题的分层�Ҏ���Q�可以将查询旉���提高到O(logn)。点定位问题的单调链�Ҏ��用O(nlogn)旉���和O(n)�I�间作预处理�Q�查询时间可以O((logn)^2)完成。点定位的三角�Ş�l�分�Ҏ��(Triangulation refinement method)只用O(n)�I�间存放预处理结果,用O(logn)旉���回答点在哪个区域�Q�完成预处理的时间是O(nlogn)。由此可见,opencascade的定位算法还有一些改�q�空间�?/p>
5. Conclusion
几何内核中曲面和曲面求交是最重要最复杂的问题,处理曲面和曲面求交需要拟合Approximation Algorithm、投影Projection Algorithm和定位Classification Algorithm工具。其中拟合和投媄主要是数学问题,定位主要是个几何问题�Q�理解问题就能找到相应的解决工具。庆�q�有opencascade�q�个功能相对完备的开源的几何内核�Q�提供了一个理������p�d���늚��q�_��。理解数学理论后可以去阅��L��码,甚至是参与和贡献�Q�求交、拟合、投影和定位工具都有一些改�q�空间�?/p>
最�q�关注的朋友说文章发得少了,主要原因是有点忙�Q�不是因��Z��守不惛_��享,当然有些朋友也提醒要留一手。对于opencascade的技术分享我是没有保留的�Q�因为opencascade是开源的�Q�如果通过�q�些文章分��n能帮助别�����决一些问题,���是创造�h��|��是有意义的。时不时收到�|�友的感谢,收获的感动不是用金钱可以衡量的�?/p>
]]>

McCad是一个开源工��P��能自动将BRep模型转换成CSG模型。随着核动力技术的发展�Q�不断开展新型反应堆的研�IӞ��反应堆的燃料形式和堆芯布�|�都较�ؓ复杂�Q�由于蒙特卡�|?MC)�Ҏ����h��强大的几何处理能力和较高的计���精���度�Q�它是模拟分析这些复杂堆芯的有效手段。通过使用McCad���复杂BRep模型转换成CSG模型�Q�CSG表示的模型可作�ؓ核反应堆芯计���蒙特卡�|?MC)�Ҏ��的输入�?/p>
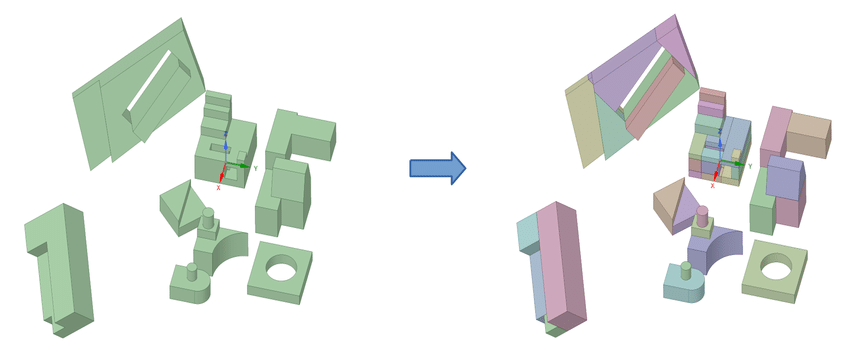
McCad��Z��OpenCASCADE内核已经持箋开发了20�q�_����Z��LGPL协议开源,感兴���的���伙伴可以下载尝试一下:
https://github.com/inr-kit/McCAD-Library
BRep转CSG个�h感觉没有完美的解��x��案,但是应用范围很广。如果�{换效果好�Q�其实还有一个用途,���是���BRep转换的CSG模型导入到PDMS中,从而解决通过机械讑֤�接口MEI导入STEP/IGES后PDMS模型数据变大的问题�?/p>
McCad is an open source tool for automatic conversion of B-Rep models into CSG.
McCad has been continuously developed for more than two decades. It provides automatic conversion of Boundary Representation (BREP) CAD models into Constructive Solid Geometry (CSG), the latter of which is an input syntax often used in Monte Carlo (MC) radiation transport codes. The conversion process, from BREP to CSG, is essential for high-fidelity nuclear analysis of complex nuclear facilities. McCad can convert CAD files in STEP format to different input syntaxes used with MC codes such as MCNP, TRIPOLI, Geant4, etc., so that the manual efforts on building a complex simulation model can be avoided. McCad provides an advanced algorithm to decompose complex solids into its constituent convex primitives, and generates the void space description between the solids, which is required by MC codes.
It relies on OpenCASCADE CAD kernel to perform CAD manipulations and Boolean operations. McCad has been integrated into the SALOME platform, with a detailed manual provided. It is an open-source code released under LGPL license. This code has been currently used for nuclear research institutes crossing continents, for nuclear analyses on fission reactors, fusion facilities and neutron source facilities.
]]>
1 Introduction
OpenCASCADE的显�C�模块的功能性能如何�Q�很多�h都很兛_��。开源社区的FreeCAD目前的显�C�功能都没有使用OpenCASCADE的显�C�模块。早�?014�q�时�Q�我在社�����坛提�����昄���模块交互选择的性能问题�Q?/p>
https://dev.opencascade.org/content/selection-convert-2d-not-very-efficient
当时的版本应该是6.8.0。在6.7.1的发布信息中�q�提��C��我很开心:

当时KGV也正在优化这部分的功能:
https://tracker.dev.opencascade.org/view.php?id=24623
通过引入BVH来更高效地处理选择�Q�这个功能集成到6.9.0的版本中了。在6.8.0版本中已�l�在增强昄���模块的性能�Q�如引入culling机制�Q?/p>
https://tracker.dev.opencascade.org/view.php?id=24307
�?.4.0版本�Q�culling基本完善�Q�当模型���出视锥体范围就从显存中去除�Q?/p>
https://tracker.dev.opencascade.org/view.php?id=30223
到现在最新版本,昄���模块的显�C�和交互功能的性能到底如何�Q�下面给出我的一个测试,���试�l�果仅供参考�?/p>
2 ����g信息
���试电脑的配�|�信息如下表�Q?/p>

�q�台电脑已经是好几年之前的配�|�了�Q�相对现在的��L��配置已经落后了�?/p>
3 ���试�l�果
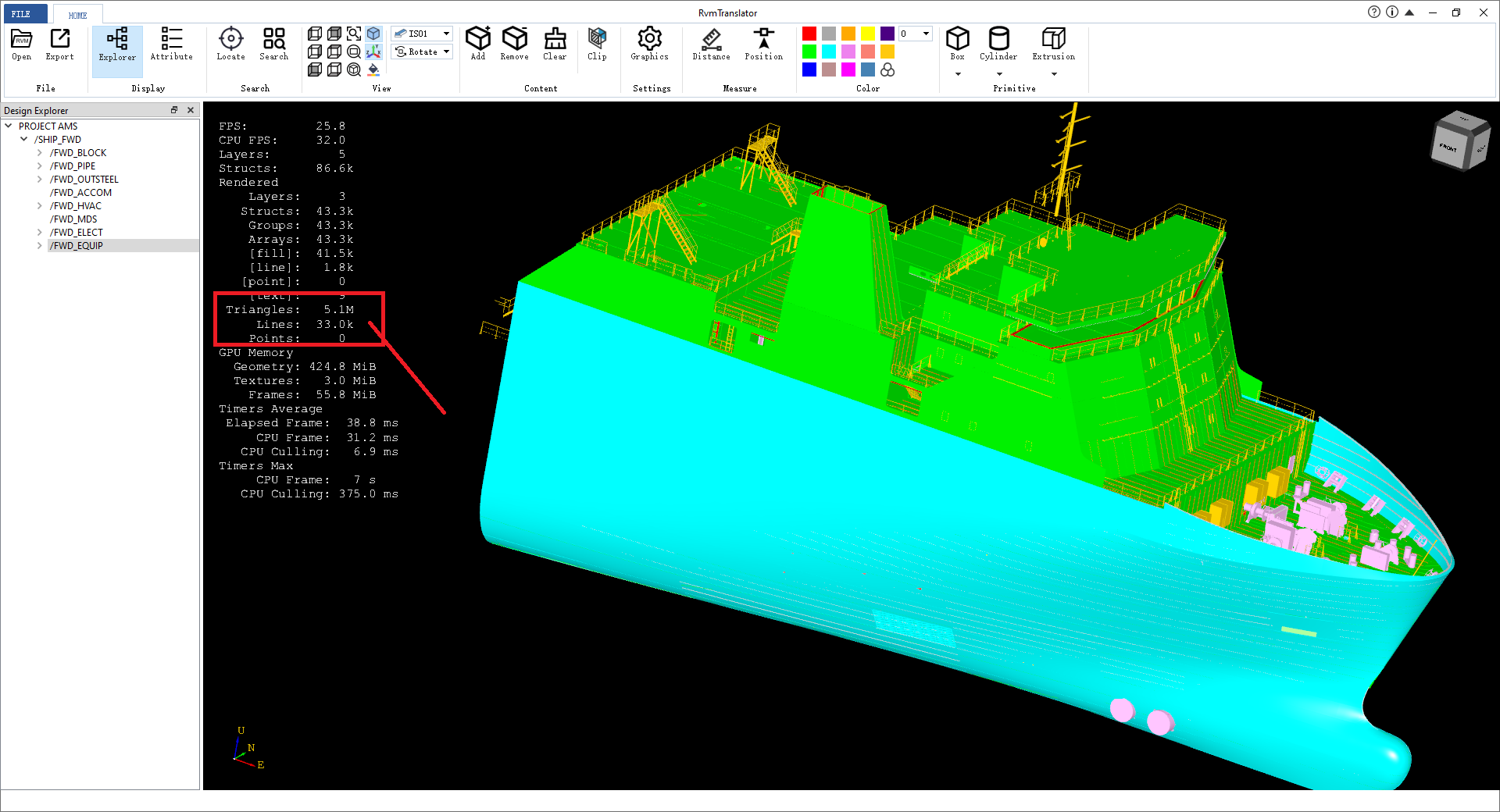
�q�个���试模型是船的艏部模型,包括船体�l�构和舾装模型,��d��的三角面片数量�ؓ5百万�Q���数FPS�?5.8�Q���数大�?2应该���流畅。交互选择性能很好�Q�感觉不到�g�q�,鼠标�U�d��到模型上���可以高亮�?/p>
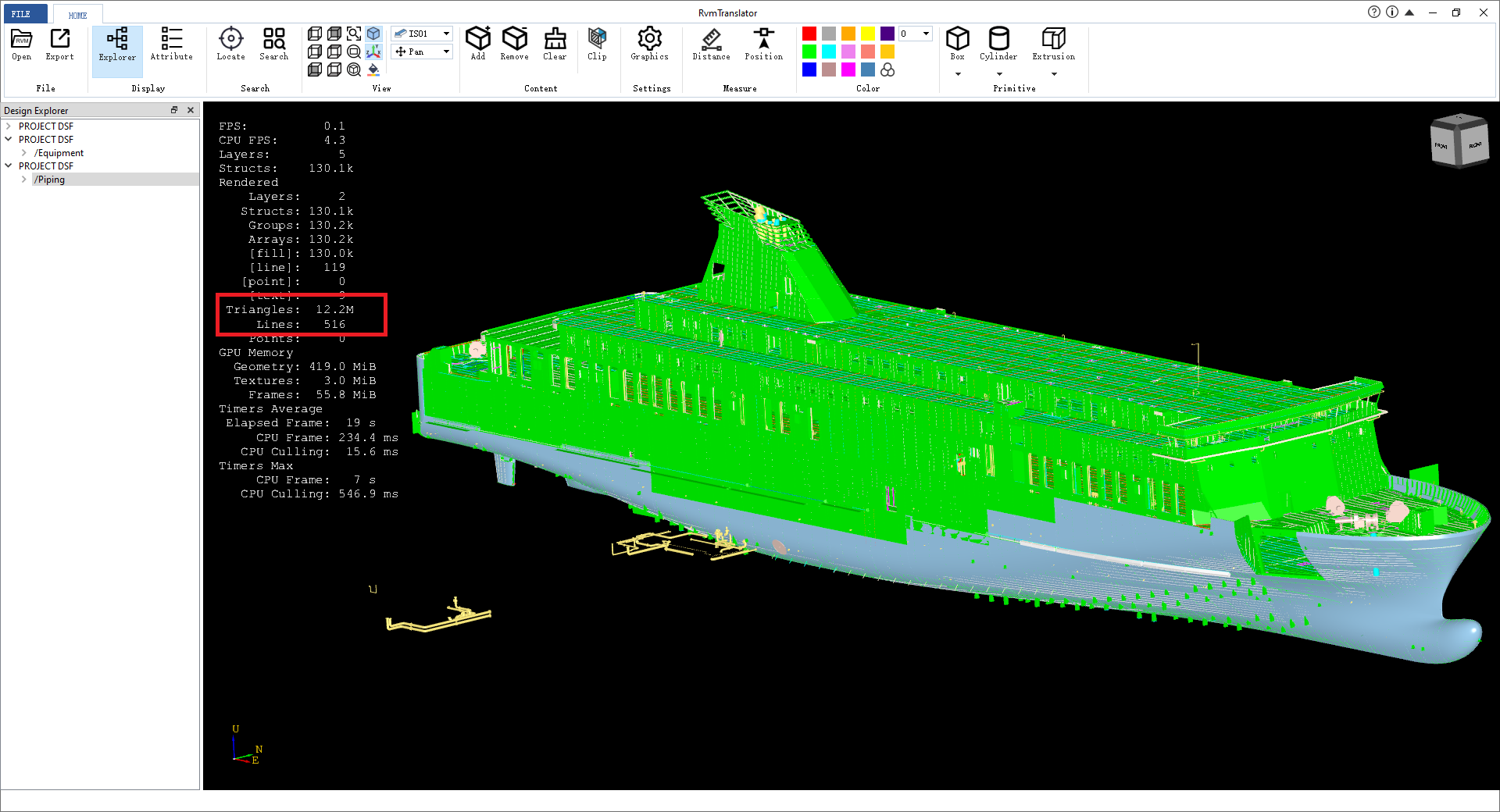
�q�个���试模型是一个渡轮,包括船体�l�构和舾装的所有模型,��d��的三角面片数量�ؓ1�?百万�Q���数FPS�?.1�Q�视图操作(对视囄���放、旋转、移动)已经有比较严重的延迟�Q�但是交互选择性能�q�不错,没有延迟�Q�鼠标移动到模型上也是实旉���亮�?/p>

�q�个是�v�z���^台模型,包括�l�构和舾装模型。这个模型量最大,��d���?�?百万三角面片�Q���数FPS�?.2�Q�视图操作(对视囄���放、旋转、移动)已经有比较严重的延迟�Q�但是交互选择性能�q�不错,没有延迟�Q�鼠标移动到模型上也是实旉���亮。这个最大的模型占用内存情况如下图所�C�:

软�g��d��占存3.4G内存�Q�这其中�q�包含左边的设计��D��树的数据。当���模型放大,���出视图范围外的模型已经被剔除culling�Q�所以可以从上图可以看出三角面片数量变少了,�?百万�?/p>
4 Conclusion
通过以上的测试数据,大家可以�l�合自己行业模型的体量来选择是否使用OpenCASCADE的显�C�模块。对于接�q?千万三角面片的模型来��_��模型量已�l�比较大�Q�在�q�个电脑配置情况下基本能满��一些大体量的模型显�C�及交互操作。因为对于大的设计模型,一般在设计�q�程中,也不是一个�h设计�Q�而是多�h多专业协同设计,一个�h涉及到的模型量一般不会达�?千万�q�个量��。而当设计完成�Q�只需要浏览时�Q�如模型评审�Q�,�q�时���有很多优化手段�?/p>
]]>