Posted on 2023-12-02 12:21
eryar 閱讀(1746)
評論(0) 編輯 收藏 引用 所屬分類:
2.OpenCASCADE

OpenCASCADE曲線上點的反求
eryar@163.com
1 Introduction
曲線可以用代數方程表示����,如圓可以用X^2+Y^2=R^2表示����,也可以用參數方程X(u)=RCos(u), Y(u)=RSin(u)表示。要判斷點是不是在線上�����,用曲線代數方程可以很直接得出結果��,但是使用參數方程就沒有那么直接����。這也是參數曲線上點的反求問題����,參數曲線上點的反求問題應用廣泛,如前面所述判斷點是否在曲線上��、點向曲線投影����、點與線的求交����、點在參數曲線上的參數等,都與點的反求問題相關。本文主要結合代碼介紹OpenCASCADE曲線上點的反求實現原理及使用過程中的一些注意事項�����。
2 實現原理
在《The NURBS Book》書中將點的反求問題歸結為點向曲線投影距離最短的問題��,如下圖所示:
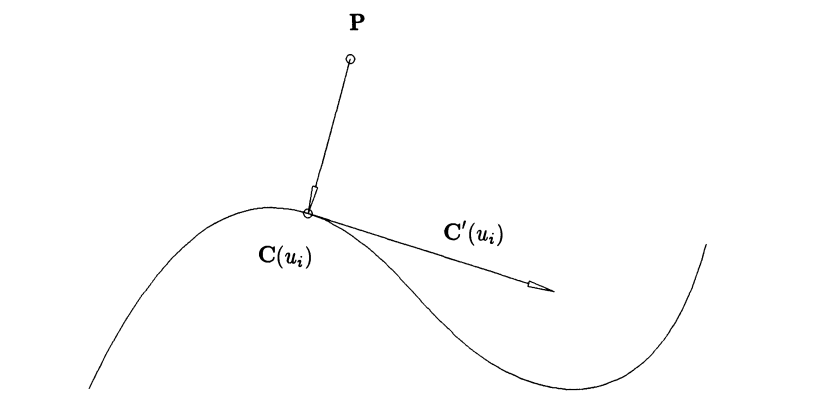
建立函數f(u)=C’(u).(C(u) - P)表示點到曲線距離��,當f(u)=0時為點到曲線的最短距離,不管點P是否在曲線上。幾何意義是點到曲線任意點的向量與任意點處的切向量點積為零�����,表示在兩個向量垂直的時候求得極值點��。注意數學方程中垂直這個幾何意義����。
OpenCASCADE中實現曲線上點的反求原理與《The NURBS Book》書中一致。點的反求使用類GeomLib_Tool::Parameter()函數:
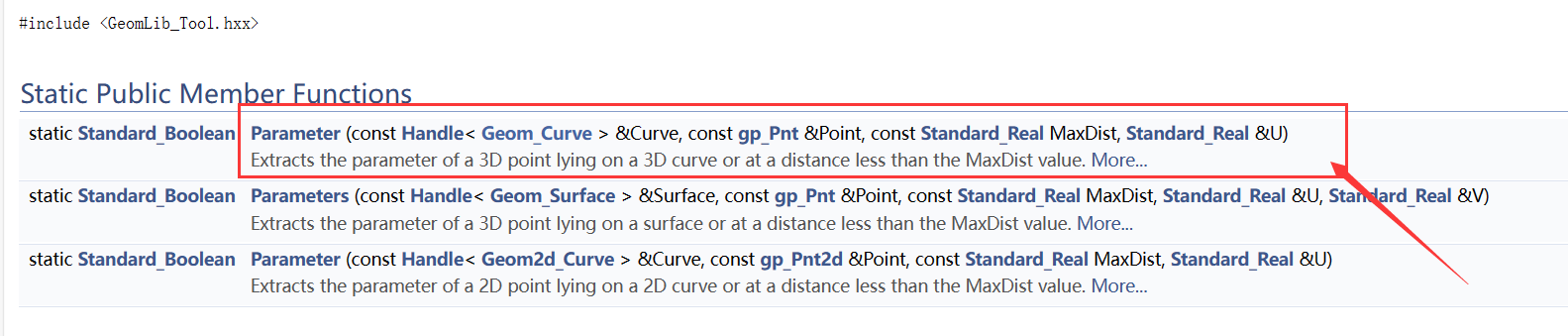
輸入曲線����、點和最大距離�����,計算點是否在曲線上及若在曲線上,點對應參數曲線的參數U����。
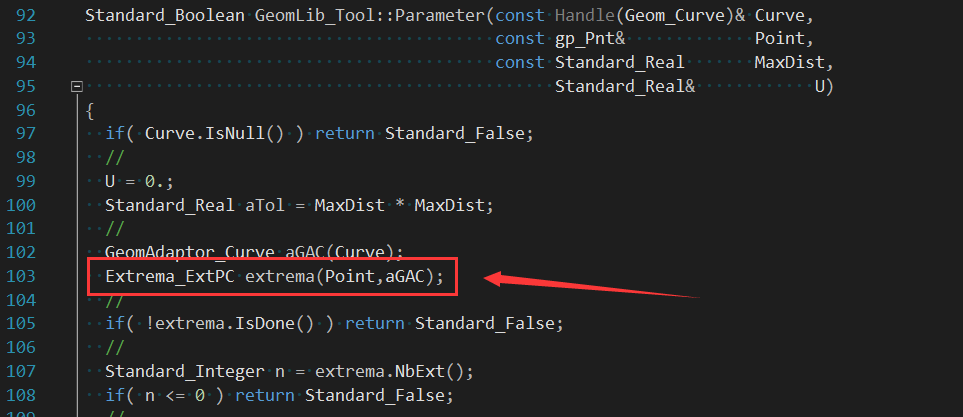
類Extrema_ExtPC計算點P到線C的極值Extrema。根據代碼注釋可以看出點的反求數學方程與《The NURBS Book》書中一致:
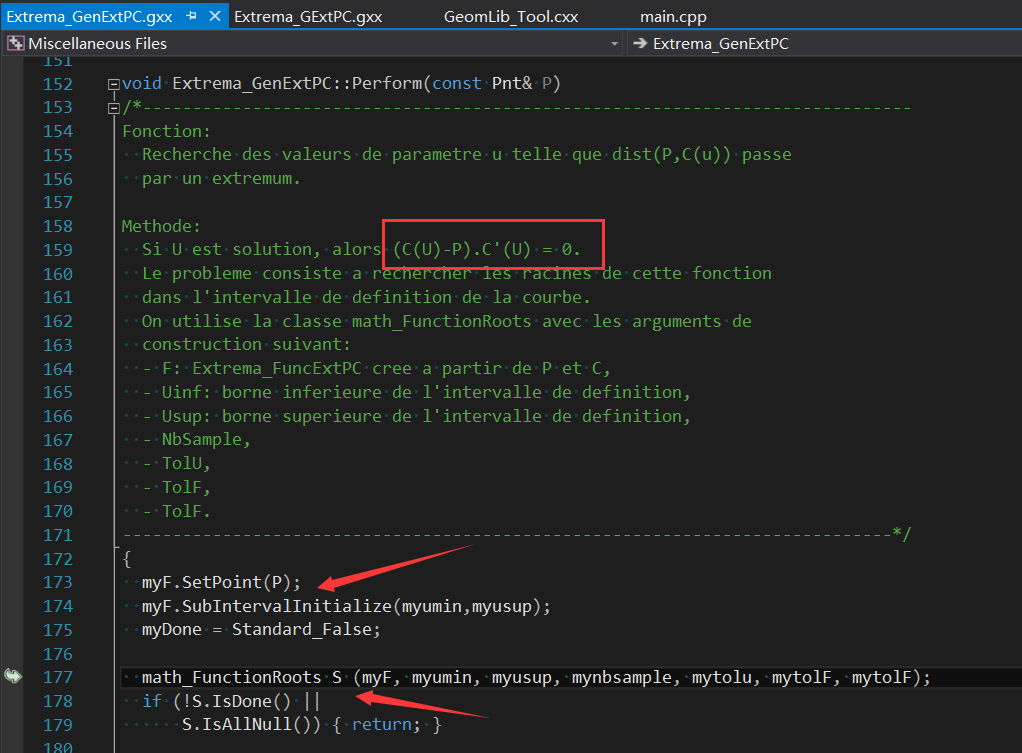
數學方程對應的類的變量為myF,類名為Extrema_FuncExtPC�����,從類math_FunctionWithDerivative派生�����,所以必須實現兩個關鍵虛函數Value()和Derivative()�����。其代碼注釋說明了這兩個函數的實現細節:

其中F(u)對應函數Value():
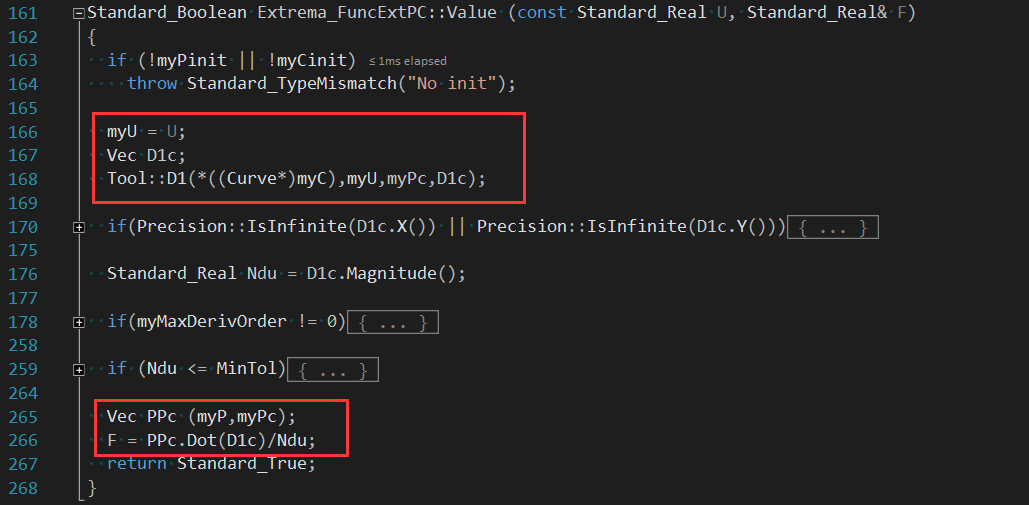
DF(u)對應函數Derivative(),最后使用Newton法math_FunctionRoots對方程進行求根����。
3 注意事項
OpenCASCADE中點的反求GeomLib_Tool::Parameter()����、點向曲線投影GeomAPI_ProjectPointOnCurve����、點與曲線的交點IntTools_Context::ComputeVE等算法都是使用了Extrema_ExtPC類。
當使用GeomLib_Tool::Parameter()函數來判斷點是否在曲線上時,注意端點處點的反求要滿足垂直的條件�����,即使點與曲線某個端點距離小于MaxDist時��,也是返回false�����。即對于曲線端點處的情況需要自己預先處理����,直接算點P與曲線端點距離與MaxDist比較,先處理端點��。

可以看到這里也處理的端點處的情況����,但是最后沒有與MaxDist有關系,最后容差是Precision::SquareConfusion()��。