дҫқжүҳдёАLөҒе·ҘеҺӮи®ҫи®ЎиҪҜдҡgж•°еӯ—еҢ–дәӨд»ҳж•°жҚ®ж–Үд»УһјҢAVEVAе…¬еҸёPDMS/E3Dзҡ„RVMе’ҢIntergraphе…¬еҸёSP3Dзҡ„VUEеQ?/p>

PlantAssistantеҸҜд»Ҙи§ЈжһҗVUEе’ҢRVMдёӯдёүҫlҙжЁЎеһӢж•°жҚ®пјҢеұһжҖ§ж•°жҚ®пјҢдҝқз•ҷи®ҫи®Ўзӣ®еҪ•ж ‘пјҢтq¶еҸҜд»Ҙе°ҶҳqҷдәӣдҝЎжҒҜиҪ¬жҚўжҲҗйҖҡз”Ёзҡ„дёүҫlҙж–Үд»¶ж јејҸпјҢеҰӮGLTF, OBJҪ{үпјҢдёәж•°еӯ—еҢ–дәӨд»ҳжҸҗдҫӣжңҚеҠЎгҖӮPlantAssistantдёүз»ҙӢ№Ҹи§ҲеҠҹиғҪе…Қиҙ№дҪҝз”ЁеQҢдШ“дёүз»ҙжЁЎеһӢиҜ„е®ЎжҸҗдҫӣдёҖдёӘиҪ»йҮҸеҢ–зҡ„е·Ҙе…—чҖ?/p>
дёүз»ҙи§Ҷеӣҫи®„ЎҪ®
ж ТҺҚ®з”ЁжҲ·еҸҚйҰҲеQҢеңЁPlantAssistantдёӯеўһеҠ и§Ҷеӣ„Ўӣёе…Ңҷ®ҫҫ|®йҖүйЎ№еQҢеҰӮи®„ЎҪ®жҳҜеҗҰжҳ„ЎӨәеқҗж ҮиҪҙгҖҒи§Ҷеӣҫж–№еқ—гҖҒдёүҫlҙи§ҶеӣҫиғҢжҷҜпјҢеҸҜд»Ҙи®„ЎҪ®иғҢжҷҜйўңиүІеQҢиҝҳеҸҜд»Ҙи®„ЎҪ®дёҖеј еӣҫзүҮдҪңдёЮZёүҫlҙи§ҶеӣҫиғҢжҷҜгҖ?/p>
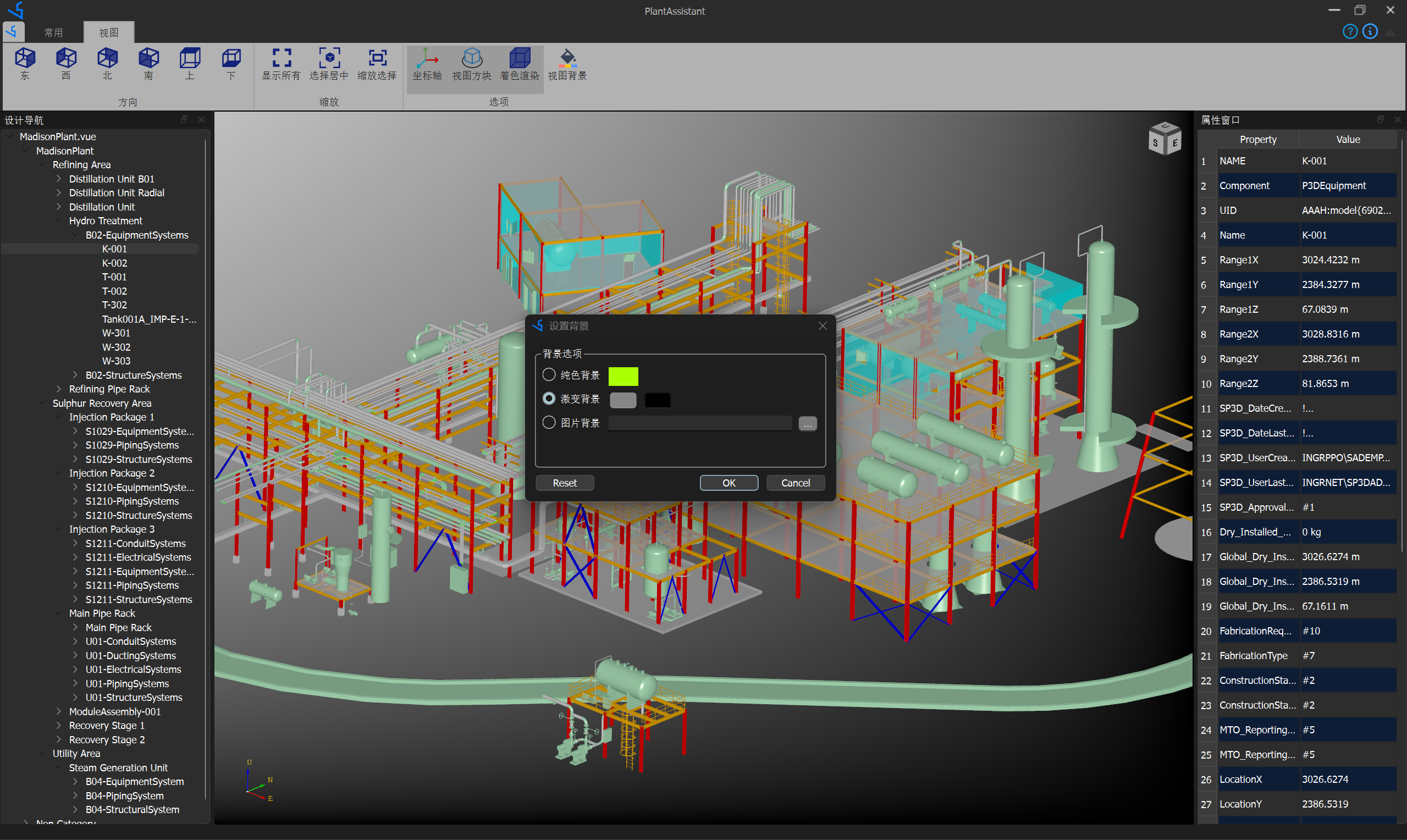
еҸҰеӨ–ҳqҳдҝ®еӨҚдёӯж–ҮжҳҫҪCЮZШ•з Ғзҡ„й—®йўҳеQҢеҢ…жӢ¬и®ҫи®Ўзӣ®еҪ•ж ‘дёҠеҗҚҝU°жҳҫҪCЮZёӯж–ҮдШ•з ҒпјҢеұһжҖ§дёӯж–ҮдШ•з ҒпјҢд»ҘеҸҠеҜјеҮәGLTFдёӯи®ҫи®Ўзӣ®еҪ•ж ‘еҗҚз§°еҸҠеұһжҖ§дёӯж–ҮдШ•з Ғй—®йўҳгҖ?/p>
дёӢиқІPlantAssistant
PlantAssistantиҪҜдҡgеңЁPipeCAD QQҫҹӨж–Ү件дёӯдёӢиқІеQҢж¬ўҳqҺеӨ§е®¶дёӢиҪҪдӢЙз”ЁеҸҚйҰҲж„Ҹи§ҒгҖ?br style="margin: 0px; padding: 0px;" />ӢЖўиҝҺеӨ§е®¶еҠ е…ҘPipeCAD QQдәӨжөҒҫҹ?964851855еQҢдәӨӢ№ҒиКYд»үҷ—®йўҳгҖҒеҝғеҫ—пјҡ
дҫқжүҳдёАLөҒе·ҘеҺӮи®ҫи®ЎиҪҜдҡgж•°еӯ—еҢ–дәӨд»ҳж•°жҚ®ж–Үд»УһјҢAVEVAе…¬еҸёPDMS/E3Dзҡ„RVMе’ҢIntergraphе…¬еҸёSP3Dзҡ„VUEеQ?/p>

жҲ‘们жғПxҠҠе·ҘеҺӮж•°еӯ—еҢ–еҠ©жүӢPlantAssistantеҒҡжҲҗеӨ§е®¶и®ҫи®Ўе·ҘдҪңдёӯзҡ„дёҖдёӘеҘҪеё®жүӢгҖӮиҝҷжҳҜжҲ‘们жһ„жғізҡ„PlantAssistantзҡ„дёҖдәӣеҠҹиғҪпјҢдё»иҰҒжҳҜеҜ№е·ҘеҺӮжЁЎеһӢҳqӣиЎҢе®ЎжҹҘгҖҒжЁЎеһӢзҡ„иҪ¬жҚўе’ҢеӨҚз”ЁеҸҠиҮӘеҠЁеҮәеӣҫеҠҹиғҪгҖ?/p>
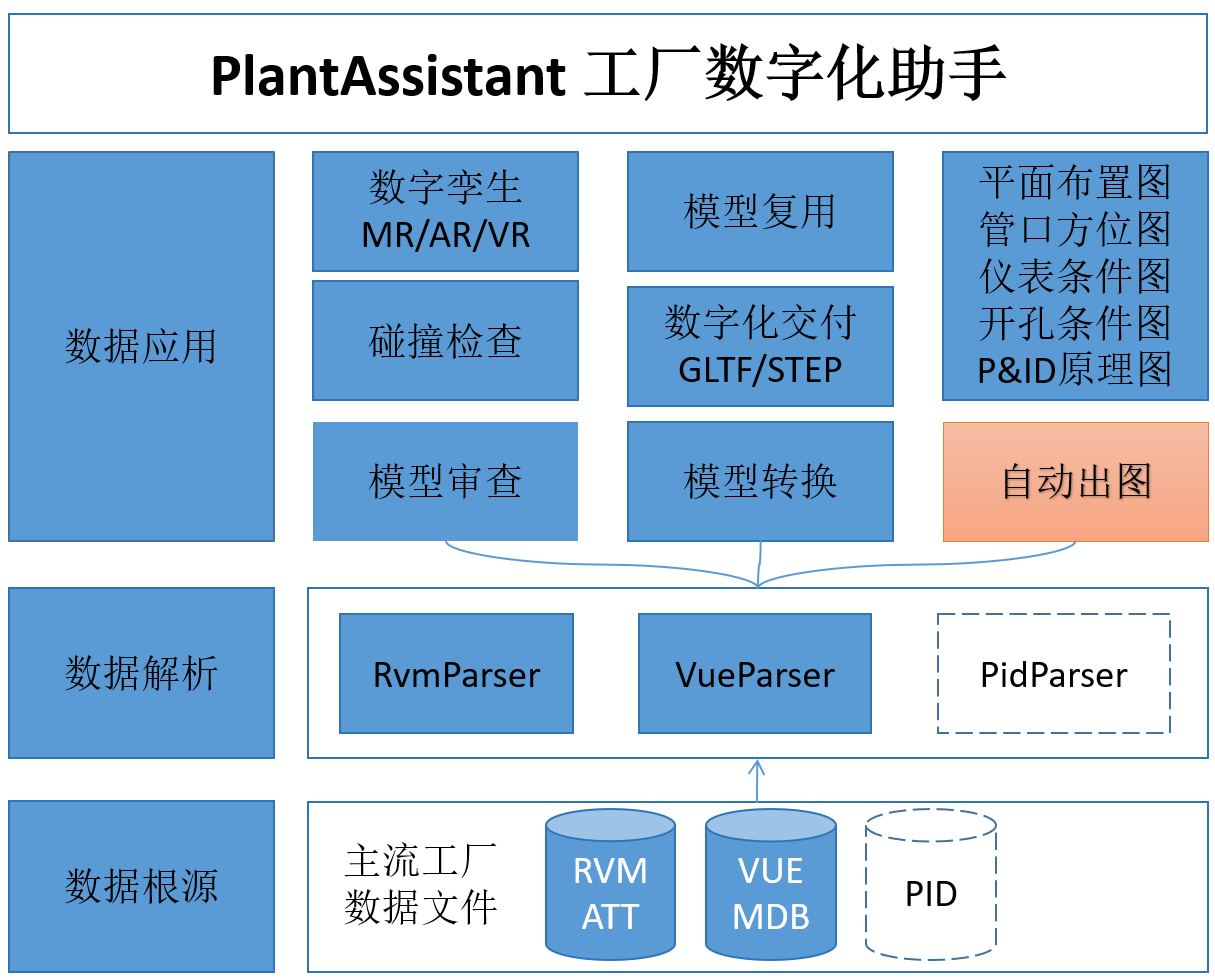
йҖҡиҝҮи§ЈжһҗҳqҷдёӨдёӘдё»Ӣ№Ғи®ҫи®ЎиКY件зҡ„ж•°жҚ®еQҢеҸҜд»Ҙе®һзҺ°е·ҘеҺӮжЁЎеһӢзҡ„дёүз»ҙеҸҜи§ҶеҢ–пјҢд»ҺиҖҢиҝӣиЎҢжЁЎеһӢзҡ„е®ЎжҹҘгҖӮзҺ°еңЁеҸ‘еёғдёҖдёӘзүҲжң¬пјҢеҸҜд»Ҙз”ЁжқҘе…Қиҙ№жҹҘзңӢRVMе’ҢVUEзҡ„дёүҫlҙжЁЎеһӢпјҢтq¶дё”иҪ»йҮҸһ®ҸейyгҖ?/p>
RVM&VUE
PlantAssistantж”ҜжҢҒӢ№Ҹи§ҲRVMжЁЎеһӢеҸҠжҹҘзңӢеҜ№еә”зҡ„еұһжҖ§пјҢзӮ№еҮ»дёүз»ҙжЁЎеһӢеҜ№иұЎеQҢдјҡиҮӘеҠЁе®ҡдҪҚеҲ°и®ҫи®ЎеҜјиҲӘж ‘еQ?/p>
PlantAssistantж”ҜжҢҒӢ№Ҹи§ҲVUEжЁЎеһӢеQҢжҡӮдёҚж”ҜжҢҒеұһжҖ§ж•°жҚ®зҡ„жҹҘзңӢеQҢжӯЈеңЁејҖеҸ‘дёӯеQҢдёӢдёӘзүҲжң¬е°Ҷдјҡж”ҜжҢҒгҖ?/p>
дёӢиқІPlantAssistant
PlantAssistantиҪҜдҡgеңЁPipeCAD QQҫҹӨж–Ү件дёӯдёӢиқІеQҢж¬ўҳqҺеӨ§е®¶дёӢиҪҪдӢЙз”ЁеҸҚйҰҲж„Ҹи§ҒгҖӮж¬ўҳqҺеӨ§е®¶еҠ е…ҘPipeCAD QQдәӨжөҒҫҹ?964851855еQҢдәӨӢ№ҒиКYд»үҷ—®йўҳгҖҒеҝғеҫ—пјҡ

еQҢз®ҖеҚ•жҳҺдә?/span>гҖӮзӣҙжҺҘеңЁж”ҝеҠЎдёӯеҝғҫ|‘з«ҷеңЁзәҝеҠһзҗҶеQҢдёҖеӨ©е°ұеҠһеҘҪдәҶпјҢҳqҳжҳҜеҫҲж–№дҫҝзҡ„еQҢд№ҹҪҺ—еҠһжҲҗдёҖ件称еҝғзҡ„дәӢжғ…гҖӮж–°зҡ„еҗҚеӯ—пјҢж–°зҡ„иөпLӮ№еQ?/p>
дә§е“ҒҪҺҖд»?/span>
е·ҘеҺӮж•°еӯ—еҢ–еҠ©жү?PlantAssistant
ҪҺЎйҒ“иҪҙжөӢеӣ‘Цј•ж“?IsoAlgo
дёүз»ҙжҷшҷғҪеҮәеӣҫиҪҜдҡg AutoDraft
дёүз»ҙҪҺЎйҒ“и®ҫи®ЎиҪҜдҡg PipeCAD
1 Introduction
з”Ёи®ЎҪҺ—жңәз”ҹжҲҗдёүз»ҙзү©дҪ“зҡ„зңҹе®һеӣҫеҪўпјҢжҳҜи®ЎҪҺ—жңәеӣ‘ЦЕһеӯҰз ”ҪI¶зҡ„йҮҚиҰҒеҶ…е®№гҖӮзңҹе®һеӣҫеҪўеңЁд»ҝзңҹжЁЎжӢҹгҖҒеҮ дҪ•йҖ еһӢгҖҒе№ҝе‘ҠеӘ„и§Ҷе’ҢҝU‘еӯҰи®Ўз®—еҸҜи§ҶеҢ–зӯүи®ёеӨҡйўҶеҹҹйғҪжңүзқҖтqҝжіӣеә”з”ЁгҖӮеңЁз”ЁжҳҫҪCшҷ®ҫеӨҮжҸҸҳq°зү©дҪ“зҡ„еӣ‘ЦЕһж—УһјҢеҝ…йЎ»жҠҠдёүҫlҙдҝЎжҒҜз»ҸҳqҮжҹҗҝUҚжҠ•еҪұеҸҳжҚўеңЁдәҢз»ҙзҡ„жҳҫҪCәег^йқўдёҠҫlҳеҲ¶еҮәжқҘгҖӮд»Һдёүз»ҙжҠ•еӘ„еҲоCәҢҫlҙзҡ„йҷҚз»ҙж“ҚдҪңеQҢдјҡеҜЖDҮҙеӣ‘ЦЕһзҡ„дәҢд№үжҖ§гҖӮиҰҒж¶ҲйҷӨҳqҷзұ»дәҢд№үжҖ§пјҢһ®ұеҝ…ҷеХdңЁҫlҳеҲ¶ж—¶ж¶ҲйҷӨиў«йҒ®жҢЎзҡ„дёҚеҸҜи§Ғзҡ„зәҝжҲ–йқўеQҢд№ жғҜдёҠҝUоC№Ӣдёәж¶ҲйҷӨйҡҗи—ҸзәҝHidden Line Removalе’Ңйҡҗи—ҸйқўHidden Face RemovalгҖ?/p>

ҳqҷжҳҜжёІжҹ“жҳ„ЎӨәдёҠеҜ№ж¶Ҳйҡҗзҡ„йңҖжұӮпјҢеңЁж №жҚ®дёүҫlҙжЁЎеһӢиҮӘеҠЁз”ҹжҲҗе·ҘҪEӢеӣҫзҡ„е·ҘҪEӢи®ҫи®ЎиКY件дёӯеQҢеҜ№ж¶Ҳйҡҗзҡ„йңҖжұӮжңүжүҖдёҚеҗҢгҖ?/p>

е·ҘзЁӢи®ҫи®ЎиҪҜдҡgдёҺжңәжў°и®ҫи®ЎиКY件дёҚеҗҢпјҢе·ҘзЁӢи®ҫи®ЎиҪҜдҡgдёҖӢЖЎеҮәеӣҫж¶Ҳйҡҗзҡ„жЁЎеһӢйҮҸеӨ§еQҢеҜ№еҮәеӣҫзҡ„з®—жі•иҰҒжұӮдё»иҰҒжңүеQ?/p>
- дё»иҰҒдҪҝз”Ёж¶ҲйҡҗҫUҝз®—жі•пјӣ
- ж¶Ҳйҡҗеҫ—еҲ°зҡ„зәҝиғҪжүҫеҲоCёҺдёүз»ҙжЁЎеһӢзҡ„е…іҫp»пјҢж–№дҫҝж ҮжіЁжЁЎеһӢдҝЎжҒҜеQҢеҰӮжЁЎеһӢеҗҚз§°гҖҒи§„ж јзӯүеQ?/li>
- иҮӘеҠЁж ҮжіЁеёғеұҖҪҺ—жі•еQҢиғҪеҜТҺ ҮжіЁзҡ„еҗҚз§°гҖҒи§„ж јзӯүиҮӘеҠЁеёғеұҖеQҢеҮҸһ®‘жүӢе·Ҙи°ғж•Я_јӣ
- иҮӘеҠЁһ®әеҜёж ҮжіЁеQ?/li>
- ҪWҰеҸ·еҢ–еӨ„зҗҶпјҢеҰӮз®ЎйҒ“жЁЎеһӢиғҪз”ЁдёҖжқЎзәҝҪWҰеҸ·еҢ–еӨ„зҗҶпјӣ
е…¶е®һжңҖеҗҺжҖИқ»“жҲҗдёҖеҸҘиҜқһ®ұжҳҜдёҖй”®ж №жҚ®жЁЎеһӢз”ҹжҲҗиғҪдәӨд»ҳзҡ„еӣҫҫUёгҖӮиҷҪ然зҺ°еңЁжҠҖжңҜдёҠе…·еӨҮдёүз»ҙжЁЎеһӢдёӢиһRй—ҙзҡ„иғҪеҠӣеQҢдҪҶжҳҜзӣ®еүҚдәҢҫlҙеӣҫҫUжҖҫқ然жҳҜи®ҫи®ЎдәӨд»ҳгҖҒеҠ е·ҘеҲ¶йҖ дё»иҰҒдҫқжҚ®гҖӮе·ҘҪEӢзұ»и®ҫи®ЎиҪҜдҡgдё»иҰҒзҡ„еҠҹиғҪе°ұжҳҜеҝ«йҖҹеҫҸжЁЎпјҢј„°ж’һӢӮҖӢ№Ӣе’ҢиҮӘеҠЁеӣ„Ўәёз”ҹжҲҗгҖӮеҪ“жЁЎеһӢйҮҸеӨ§ж—УһјҢж¶ҲйҡҗйҖҹеәҰеҝ«еҸҠиҮӘеҠЁз”ҹжҲҗзҡ„ж ҮжіЁж–Үеӯ—жҺ’еҲ—ж•ҙйҪҗпјҲжҲ–ж»Ўӯ‘ӣ_·ҘҪEӢд№ жғҜпјүжҲҗдәҶдәҢз»ҙеӣ„ЎәёиҮӘеҠЁз”ҹжҲҗзҡ„ж ёеҝғжҠҖжңҜпјҢд№ҹжҳҜҪEӢеәҸеӨ„зҗҶдёӯзҡ„йҡ„ЎӮ№гҖ?/p>
2 HLR
еҮ дҪ•еҶ…ж ёдёҖиҲ¬йғҪжҸҗдҫӣHLRҪҺ—жі•еQҢз”ЁжқҘж №жҚ®жЁЎеһӢжҠ•еҪЮq”ҹжҲҗдәҢҫlҙе·ҘҪEӢеӣҫгҖӮOpenCASCADEзҡ„HLRжҸҗдҫӣдәҶйҡҗи—Ҹзәҝж¶ҲйҡҗҪҺ—жі•гҖ?/p>

https://www.spatial.com/zh/products/cgm-hlr-hidden-line-removal
OpenCASCADE жҸҗдҫӣдәҶдёӨҝUҚж¶Ҳйҡҗз®—жі•пјҡHLRBRep_Algoе’ҢHLRBRep_PolyAlgoгҖӮиҝҷдәӣз®—жі•йғҪжҳҜеҹәдәҺзӣёеҗҢзҡ„еҺҹзҗҶеQҡжҜ”иҫғеЕһзҠ¶жҜҸжқЎиҫ№зӣёеҜ№жҜҸдёӘйқўзҡ„еҸҜи§ҒжҖ§пјҢтq?и®Ўз®—жҜҸжқЎиҫ№зҡ„еҸҜи§ҒйғЁеҲҶдёҺж¶ҲйҡҗйғЁеҲҶгҖӮз®—жі•йҖҡиҝҮи®Ўз®—еңЁжҢҮе®ҡжҠ•еҪұж–№еҗ‘дёҠзҡ„зү©дҪ“жҳҫҪCәзү№жҖ§пјҢеҺ»йҷӨжҲ–ж Үи®°иў«йқўйҒ®жҢЎзҡ„иҫҸVҖӮиҝҷдёӨдёӘҪҺ—жі•д№ҹдёҺдёҖдәӣжҸҗеҸ–еҠҹиғҪй…ҚеҗҲдӢЙз”ЁпјҢеҰӮйҮҚжһ„дёҖ дёӘз®ҖеҢ–зҡ„жЁЎеһӢҪ{үпјҢҪҺҖеҢ–еҗҺж–°зҡ„жЁЎеһӢз”Юpҫ№ҫl„жҲҗеQҢе°ұжҳҜеңЁжҠ•еӘ„ж–№еҗ‘дёҠзҡ„иҪ®е»“ҫUСқҖ?/p>
3 иҫ№зҡ„еҲҶзұ»
OpenCASCADEзҡ„HLRдёӯе°Ҷиҫ№еҲҶдёЮZ»ҘдёӢзұ»еһӢпјҡ
- Sharp Edges
- Smooth Edges
- Sewn Edges
- Outline Edges
- Isoparameter Edges
д»Һзұ»HLRBRep_HLRToShapeе’Ңзұ»HLRBRep_PolyHLRToShapeдёӯз»ҷеҮЮZәҶҳqҷдәӣиҫ№зҡ„дёҖдәӣе®ҡд№үгҖӮе…¶дёӯSharp EdgeиЎЁзӨәC0ҳqһз®ӢеQҲйқһG1ҳqһз®ӢеQүзҡ„иҫ№пјҢһ®ұжҳҜдёҖиҲ¬EdgeеQ?/p>
Smooth EdgeиЎЁзӨәG1ҳqһз®ӢеQҲйқһG2 ҳqһз®ӢеQүзҡ„иҫ№пјӣ
Sewn EdgeиЎЁзӨәG2ҳqһз®Ӣзҡ„иҫ№еQ?/p>
Outline EdgeиЎЁзӨәжЁЎеһӢзҡ„иҪ®е»“иҫ№еQҢиҝҷҝUҚзұ»еһӢзҡ„иҫ№дёҚеңЁBREPж•°жҚ®дёӯпјҢйңҖиҰҒж №жҚ®жҠ•еҪұж–№еҗ‘з”ҹжҲҗпјӣ
Isoparameter EdgeиЎЁзӨәйқўзҡ„Ҫ{үеҸӮҫUҝз”ҹжҲҗзҡ„иҫ№пјҢҳqҷз§ҚҫcХdһӢзҡ„иҫ№дёҚд№ҹдёҚеңЁBREPж•°жҚ®дёӯпјӣ

е…¶дёӯSharp EdgeгҖҒSmooth Edgeе’ҢSewn EdgeдёҖиҲ¬йғҪжҳҜBREPдёӯзҡ„EDGEж•°жҚ®еQҢиҖҢOutline Edgeе’ҢIsoparameter EdgeжҳҜж №жҚ®и®ҫҫ|®йўқеӨ–з”ҹжҲҗзҡ„иҫҸVҖӮзҗҶи§Јиҫ№зҡ„иҝҷдәӣе®ҡд№үпјҢж–№дҫҝеҜ№HLRҪҺ—жі•ҳqӣиЎҢзҗҶи§ЈгҖӮHLRҪҺ—жі•жҳҜзӣёеҜ№з®ҖеҚ•зҡ„ҪҺ—жі•еQҢдё»иҰҒжҳҜһ®ұе°ҶдёҠиҝ°дә”з§ҚҫcХdһӢзҡ„иҫ№дёҺйқўҳqӣиЎҢжұӮдәӨеQҢеҲӨж–ӯйҒ®жҢЎе…іҫp…RҖ?/p>
зӣ®еүҚOpenCASCADEдёӯзҡ„HLRҪҺ—жі•д»Јз ҒеҶҷеҫ—жңүзӮ№д№ұпјҢдёҠж¬ЎеңЁж·ұеңіoggзҡ„дҝ„ҫ|—ж–ҜејҖеҸ‘дқhе‘ҳжҸҗеҲ°иҰҒйҮҚжһ„HLRйғЁеҲҶзҡ„д»Јз ҒгҖӮж·ұе…ҘзҗҶи§?HLRҪҺ—жі•еQҢдШ“иҮӘеҠЁз”ҹжҲҗеӣ„ЎәёеҠҹиғҪжү“дёӢеҹәзЎҖгҖ?/p>
eryar@163.com
1 Introduction
OpenCASCADEдёӯеҮ дҪ•жӣІҫUҝдёҺжӣІйқўжұӮдәӨдҪҝз”Ёҫc»GeomAPI_IntCSеQҢжҳҜеҜ№зұ»IntCurveSurface_HInterзҡ„з®ҖеҚ•е°ҒиЈ…гҖӮеңЁIntCurveSurface_HInterдёӯеҜ№жӣІзәҝе’ҢжӣІйқўжұӮдәӨеҲҶдёЮZ»ҘдёӢеҮ ҝUҚзұ»еһӢпјҡ
- PerformConicSurfеQҡдәҢӢЖЎжӣІҫUҝдёҺжӣІйқўжұӮдәӨеQҢе…¶дёӯеҸҲеҲҶдШ“дёӨзұ»еQҡдәҢӢЖЎжӣІҫUҝдёҺдәҢж¬ЎжӣІйқўжұӮдәӨе’ҢдәҢӢЖЎжӣІҫUҝе’ҢиҮӘз”ұжӣІйқўжұӮдәӨеQ?/li>
- InternalPerformCurveQuadricеQҡиҮӘз”ұжӣІҫUҝдёҺдәҢж¬ЎжӣІйқўжұӮдәӨеQ?/li>
- InternalPerformеQҡиҮӘз”ұжӣІҫUҝе’ҢиҮӘз”ұжӣІйқўжұӮдәӨеQ?/li>
жң¬ж–Үдё»иҰҒд»Ӣз»ҚжӣІзәҝдёҺжӣІйқўжұӮдәӨзҡ„е®һзҺ°еҺҹзҗҶгҖ?/p>
2 дәҢж¬ЎжӣІзәҝдёҺдәҢӢЖЎжӣІйқўжұӮдә?/h2>
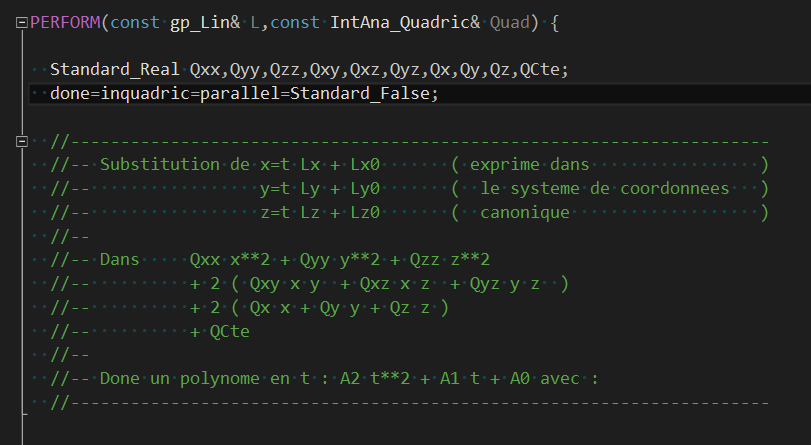
дәҢж¬ЎжӣІзәҝдёҺдәҢӢЖЎжӣІйқўжұӮдәӨдӢЙз”ЁIntAna_ConicQuadи®Ўз®—еQҢдё»иҰҒжҖқиө\жҳҜе°ҶжӣІзәҝз”ЁеҸӮж•°ж–№ҪEӢиЎЁҪCәпјҢд»Је…ҘдәҢж¬ЎжӣІйқўзҡ„д»Јж•°ж–№ҪEӢгҖӮдәҢӢЖЎжӣІйқўеҸҜд»ҘдӢЙз”ЁдәҢӢЖЎеӨҡҷе№ејҸиЎЁзӨәеQҢе°ҶдәҢж¬ЎжӣІзәҝдёҺдәҢӢЖЎжӣІйқўзӣёдәӨиЎЁҪCәжҲҗдёҖдёӘеӨҡҷе№ејҸж–№зЁӢеQҢдӢЙз”Ёmath_DirectPolynomialRootsеҜ№еӨҡҷе№ејҸж–№зЁӢҳqӣиЎҢжұӮи§ЈгҖ?/p>
3 дәҢж¬ЎжӣІзәҝдёҺиҮӘз”ұжӣІйқўжұӮдә?/h2>
дәҢж¬ЎжӣІзәҝдёҺиҮӘз”ұжӣІйқўжұӮдәӨе°ҶжӣІйқўдҪҝз”ЁIntCurveSurface_PolyhedronеңЁUеQҢVдёҠйҮҮж пLҰ»ж•Јеҫ—еҲ°gridҫ|‘ж јгҖӮиҝҷдёӘзұ»е®һзҺ°дёҺIntPolyh_MaillageAffinageҫcХdҠҹиғҪжңүйҮҚеӨҚгҖ?/p>
IntCurveSurface_ThePolygonеӨҡж®өҫUҝдёҺIntf_InterferencePolygonPolyhedron ҫ|‘ж јжұӮдәӨеQҢж №жҚ®еӨҡҢDлҠәҝдёҺзҪ‘ж јжұӮдәӨжғ…еҶөпјҢжү‘ЦҲ°еҲқе§ӢеҖы|јҢдҪҝз”ЁIntImp_IntCSи®Ўз®—ҫ_„ЎЎ®еҖ№{ҖӮдёҺжӣІйқўжұӮдәӨзҡ„MarchingҪҺ—жі•ҫcЦMјјеQҢдӢЙз”Ёи„Pд»Јжі•еҺ»и®ЎҪҺ—зІҫјӢ®дәӨзӮҸVҖӮи„Pд»Јж–№ҪEӢдШ“IntImp_ZerCSParFuncеQҢеҶҷеҮшҷҝҷдёӘж–№ҪEӢзҡ„Value()еҖЖD®ЎҪҺ—е’ҢDerivatives()еҫ®еҲҶи®Ўз®—е…¬ејҸгҖ?/p>
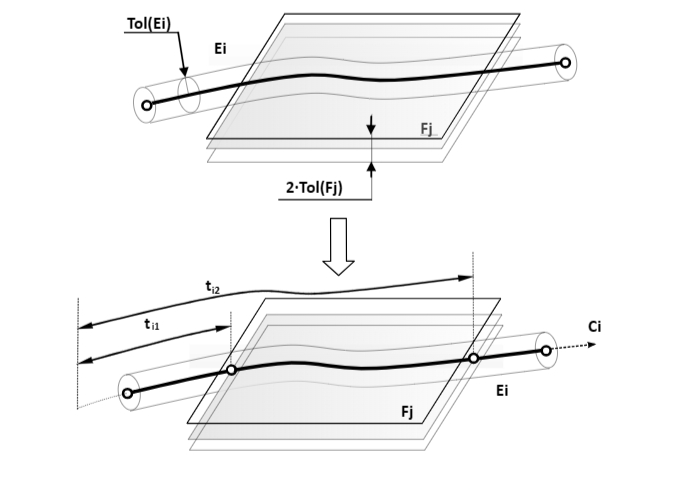
һ®ҶжӣІҫUҝдёҺжӣІйқўжұӮдәӨй—®йўҳиҪ¬еҢ–дёәжұӮжӣІйқўеҸӮж•°u,vе’ҢжӣІҫUҝеҸӮж•°wеQҢдӢЙжӣІзәҝC(w)жӣІйқўS(u,v)дёҠзҡ„зӮҡwҮҚеҗҲпјҢе»әз«ӢеҮҪж•°еҰӮдёӢеQ?/p>
F(u,v,w)=S(u,v) - C(w)
жүҖжұӮзҡ„ҫ_„ЎЎ®дәӨзӮ№ж»Ўиғцж–№зЁӢF(u,v,w)=0еQҢFдёЮZёҖеҗ«жңүдёүдёӘеқҗж Үзҡ„зҹўйҮҸпјҢеҜ№еә”еҮҪж•°Value()еQ?/p>
Fx(u,v,w)=Sx(u,v) - Cx(w) = 0
Fy(u,v,w)=Sy(u,v) - Cy(w) = 0
Fz(u,v,w)=Sz(u,v) - Cz(w) = 0
дёҠйқўдёәеҗ«жңүдёүдёӘж–№ҪEӢзҡ„д»Ҙu,v,wдёәеҸҳйҮҸзҡ„йқһзәҝжҖ§ж–№ҪEӢз»„еQҢзІҫјӢ®дәӨзӮ№е°ұжҳҜйқһҫUҝжҖ§ж–№ҪEӢз»„зҡ„и§ЈгҖӮдӢЙз”Ёзұ»math_FunctionSetRootеә”з”ЁNewton-Raphsonҳqӯд»Јжі•жұӮи§ЈйқһҫUҝжҖ§ж–№ҪEӢз»„зҡ„и§ЈгҖӮдӢЙз”ЁNewtonҳqӯд»Јжі•жңүдёӘеүҚжҸҗжқЎд»¶жҳҜиҰҒжұӮйқһзәҝжҖ§ж–№ҪEӢз»„дёҖйҳ¶еҸҜеҜы|јҢеҚҢҷҰҒеҶҷеҮәJacobianҳqӯд»Јзҹ©йҳөеQҢеҚідёҠиҝ°еҮҪж•°Derivatives()зҡ„е®һзҺ°еҺҹзҗҶпјҡ
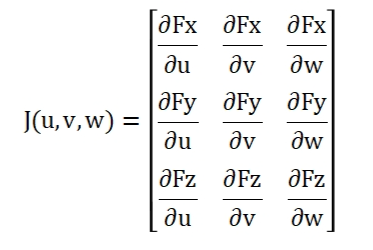
4 иҮӘз”ұжӣІзәҝдёҺдәҢӢЖЎжӣІйқўжұӮдә?/h2>
иҮӘз”ұжӣІзәҝдёҺдәҢӢЖЎжӣІйқўжұӮдәӨIntCurveSurface_TheQuadCurvExactInter еQҢйҖҡиҝҮҫc»IntCurveSurface_TheQuadCurvFuncOfTheQuadCurvExactHInterе»әз«ӢдәҢж¬ЎжӣІйқўдёҺжӣІҫUҝд№Ӣй—ҙзҡ„еҮҪж•°еQҢжҳҜжұӮи§ЈжӣІзәҝдёҠеҸӮж•°Uзҡ„дёҖе…ғеҮҪж•°гҖ?/p>
5 иҮӘз”ұжӣІзәҝдёҺиҮӘз”ұжӣІйқўжұӮдә?/h2>
иҮӘз”ұжӣІзәҝдёҺиҮӘз”ұжӣІйқўжұӮдәӨе’ҢдәҢз»ҙиҮӘз”ұжӣІзәҝжұӮдәӨҫcЦMјјеQҢйҮҮз”Ёзҡ„јӣАL•Јжі•гҖӮеҚіһ®ҶжӣІҫUүKҖҡиҝҮйҮҮж ·јӣАL•ЈжҲҗеӨҡҢDлҠәҝPolygonеQҢе°ҶжӣІйқўйҮҮж ·з”ҹжҲҗҫ|‘ж јPolyhedronеQҢйҖҡиҝҮҫc»IntCurveSurface_TheInterferenceOfHInterжқҘи®ЎҪҺ—еӨҡҢDлҠәҝдёҺзҪ‘ж јзҡ„зӣжҖәӨгҖ?/p>
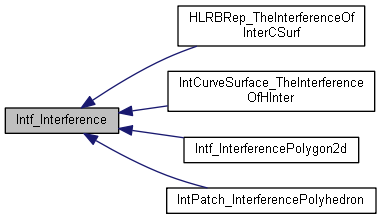
еҢ…Intfдё»иҰҒз”ЁжқҘи®Ўз®—дәҢз»ҙеӨҡж®өҫUСқҖҒдёүҫlҙеӨҡҢDлҠәҝеҸҠзҪ‘ж јзҡ„зӣжҖәӨгҖӮж №жҚ®зҰ»ж•Ји®ЎҪҺ—зҡ„ҫ_—дәӨзӮ№пјҢеҶҚж №жҚ®зұ»IntCurveSurface_TheExactHInterдҪҝз”Ёҳqӯд»Јжі•жұӮеҫ—зІҫјӢ®дәӨзӮҸVҖӮиҝҷдёӘжҖқжғідёҺжӣІйқўе’ҢжӣІйқўжұӮдәӨзӣёеҗҢгҖ?/p>
6 жұӮдәӨҫl“жһң
жӣІзәҝдёҺжӣІйқўжұӮдәӨзҡ„ҫl“жһңдё»иҰҒд№ҹжҳҜдҝқеӯҳеңЁзұ»IntCurveSurface_IntersectionеҜ№иұЎдёӯпјҢҳqҷдёӘҫcИқҡ„и®ҫи®ЎдёҺдәҢҫlҙжӣІҫUҝжұӮдәӨзұ»дјы|јҢдёҚеӨҹзӣҙжҺҘгҖ?/p>
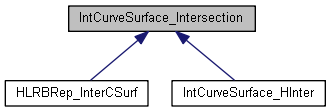
еҸҜд»ҘзңӢеҲ°IntCurveSurface_IntersectionҳqҷдёӘҫcИқҡ„жһ„йҖ еҮҪж•°жҳҜprotectedзҡ„пјҢж„ҸжҖқжҳҜдёҚиғҪзӣҙжҺҘдҪҝз”ЁеQҢйҖҡиҝҮӢz„Ў”ҹҫc»IntCurveSurface_HInterи°ғз”ЁSetValues()еҮҪж•°һ®ҶжұӮдәӨз»“жһңдҝқеӯҳи“vжқҘгҖӮжұӮдәӨз»“жһңдШ“дәӨзӮ№IntCurveSurface_IntersectionPointе’ҢдәӨҫUҝIntCurveSurface_IntersectionSegmentгҖ?/p>
е…¶дёӯдәӨзӮ№дёӯIntCurveSurface_IntersectionPointдҝқеӯҳдәҶдёүҫlҙеқҗж ҮзӮ№еQҢдәӨзӮ№еңЁжӣІйқўдёҠзҡ„U,VеҸӮж•°еQҢдәӨзӮ№еңЁжӣІзәҝдёҠзҡ„еҸӮж•°UеҸҠзӣёдәӨзҠ¶жҖҒгҖӮдәӨҫUҝдё»иҰҒжҳҜҫUҝзҺ°йқўе’ҢйҮҚеҗҲйғЁеҲҶзҡ„еҮ дҪ•еҘҮејӮжғ…еҶү|•°жҚ®гҖ?/p>
д»Һзұ»еӣҫдёҠеҸҜд»ҘзңӢеҮәеQҢиҝҷдёӘеҘ—и·ҜеҗҢж пL”ЁеҲоCәҶHLRҪҺ—жі•дёӯпјҢзҗҶи§ЈҳqҷдёӘеҘ—иө\еҜ№зҗҶи§ЈHLRҪҺ—жі•жңүеё®еҠ©гҖ?/p>
7 Conclusion
ҫlйgёҠжүҖҳqҺНјҢOpenCASCADEдёӯе°ҶжӣІзәҝдёҺжӣІйқўжұӮдәӨж №жҚ®жӣІҫUҝе’ҢжӣІйқўҫcХdһӢзҡ„дёҚеҗҢеҲҶеҲ«еӨ„зҗҶгҖӮдәҢӢЖЎжӣІҫUҝжӣІйқўжұӮдәӨдҫқиө–IntAnaеҢ…пјҢиҮӘз”ұжӣІзәҝе’ҢиҮӘз”ұжӣІйқўжұӮдәӨдӢЙз”ЁзҰ»ж•Јжі•еQҢжңҖҫlҲе®һзҺ°з®—жі•дёҺдёӨдёӘжӣІйқўжұӮдәӨзҡ„MarchingҪҺ—жі•ҫcЦMјјеQҢйҖҡиҝҮјӣАL•Јеҫ—еҲ°зҡ„зІҫдәӨзӮ№еQҢеҶҚд»Је…Ҙҳqӯд»Јж–№зЁӢжұӮеҫ—ҫ_„ЎЎ®и§ЈгҖӮе…¶дёӯжҠҠжӣІзәҝжҲ–жӣІйқўзҰ»ж•Јзҡ„йҮҮж ·зӮТҺІЎжңүиҖғиҷ‘жӣІзәҝжҲ–жӣІйқўзҡ„жӣІзҺҮҪ{үпјҢйҮҮж ·зӮТҺ•°йҮҸиҫғеӨ§пјҢдјҡеӘ„е“ҚжҖ§иғҪ гҖӮжӣІйқўйҮҮж пLҰ»ж•Јд»Јз ҒдёҺжӣІйқўжұӮдәӨдёӯзҡ„жңүйҮҚеӨҚгҖӮд»ҺеҮ дҪ•жұӮдәӨҫcЦMёӯеҸҜд»ҘзңӢеҲ°жІЎжңүе®№е·®зҡ„иҫ“е…ҘпјҢеҸҜд»ҘжҖқиҖғдёҖдёӢиҝҷдёӘй—®йўҳгҖ?/p>
TKGeomAlgoдёӯйҷӨдәҶжӢҹеҗҲз®—жі•еӨ–еQҢеӨ§йғЁеҲҶд»Јз Ғдё»иҰҒһ®ұжҳҜҫUҝзәҝжұӮдәӨгҖҒзәҝйқўжұӮдәӨеҸҠйқўйқўжұӮдәӨҪҺ—жі•гҖӮзҗҶи§Јиҝҷдәӣз®—жі•зҡ„е®һзҺ°еҺҹзҗҶеQҢдШ“BooleanҪҺ—жі•зҡ„жұӮдәӨйҖ»иҫ‘жү“дёӢеҹәзЎҖгҖ?/p>
1 Introduction
OpenCASCADEдёӯеҜ№дәҢз»ҙжӣІзәҝжұӮдәӨе’ҢдёүҫlҙжӣІҫUҝжұӮдәӨжҳҜдёҚеҗҢзҡ„пјҢдёүз»ҙжӣІзәҝжұӮдәӨҫlҹдёҖдҪҝз”ЁјӣАL•Јжі•пјҢдәҢз»ҙжӣІзәҝжұӮдәӨж ТҺҚ®жӣІзәҝҫcХdһӢзҡ„дёҚеҗҢеҲҶҝUҚзұ»еһӢиҝӣиЎҢеӨ„зҗҶгҖӮдәҢҫlҙжӣІҫUҝжұӮдәӨдёӯҳqҳжҸҗдҫӣдәҶи®Ўз®—иҮӘдәӨзҡ„зӣҙжҺҘжҺҘеҸЈгҖӮеңЁTKGeomAlgoдёӯпјҢдё»иҰҒеҶ…е®№һ®ұжҳҜжӢҹеҗҲгҖҒжұӮдәӨз®—жі•пјҢзҗҶи§ЈжұӮдәӨҪҺ—жі•зҡ„е®һзҺ°еҺҹзҗҶпјҢиҫ‘ЦҲ°иғҪйҳ…иҜХd’Ңдҝ®ж”№жәҗз Ғзҡ„зҠ¶жҖҒпјҢиғҪеӨҹеҲҶжһҗе’Ңи§ЈеҶӣ_®һйҷ…йҒҮеҲ°зҡ„й—®йўҳеQҢзҗҶи§ЈOpenCASCADEзҡ„иғҪеҠӣиҫ№з•ҢпјҢж ТҺҚ®йңҖиҰҒйҖүжӢ©жүҖйңҖиҰҒзҡ„еҠҹиғҪеQҢдӢЙиҪҜдҡgҫl“жһңеҸҜжҺ§гҖӮжң¬ж–Үдё»иҰҒд»ӢҫlҚдәҢҫlҙжӣІҫUҝзӣёдәӨзҡ„е®һзҺ°еҺҹзҗҶгҖ?/p>
з”ЧғәҺOpenCASCADEејҖеҸ‘ж—¶й—ҙзӣёеҜ№д№…ҳqңпјҢеңЁдәҢҫlҙжӣІҫUҝжұӮдәӨзӣёе…ід»Јз ҒдёӯеӨ§йҮҸдҪҝз”ЁдәҶе®Ҹе®ҡд№үзҡ„ж–№ејҸжқҘе®һзҺ°C++ зҡ„жЁЎжқҝtemplateиғҪеҠӣеQҢе®Ҹе®ҡд№үеңЁзұ»зҡ„XXX_0.cxxж–ҮдҡgдёӯпјҢеҜ№еә”жЁЎжқҝе®һзҺ°ең?.gxxдёӯпјҡ
ҳqҷз§Қе®һзҺ°ж–№ејҸдјҡи®©д»Јз Ғзҡ„еҸҜиҜАLҖ§еҸҳе·®пјҢдёҚеҲ©дәҺд»Јз Ғз»ҙжҠӨгҖӮеә”иҜҘз”ЁC++зҡ„ж–№ејҸеҜ№ҳqҷдәӣ*.gxxд»Јз ҒйҮҚжһ„еQҢеўһејЮZ»Јз ҒеҸҜиҜАLҖ§е’ҢеҸҜз»ҙжҠӨжҖ§гҖ?/p>
2 жұӮдәӨеҲҶзұ»
дәҢз»ҙжұӮдәӨдҪҝз”Ёҫc»Geom2dAPI_InterCurveCurveеQ?ҳqҷдёӘҫcАLҳҜеҜ№зұ»Geom2dInt_GInterзҡ„е°ҒиЈ…гҖӮеңЁҫc»Geom2dInt_GInterдёӯпјҢеҰӮжһңеҸӘиҫ“е…ҘдёҖжқЎжӣІҫUҝпјҢеҸҜд»Ҙи®Ўз®—иҮӘдәӨеQҢеҰӮжһңиҫ“е…ҘдёӨжқЎжӣІҫUҝпјҢи®Ўз®—дёӨжқЎжӣІзәҝзҡ„зӣёдәӨгҖ?/p>
- IntCurve_IntConicConicеQҡдәҢӢЖЎжӣІҫUҝдёҺдәҢж¬ЎжӣІзәҝжұӮдәӨгҖӮдәҢӢЖЎжӣІҫUҝдёҺдәҢж¬ЎжӣІзәҝжұӮдәӨйғҪе…ҲдҪҝз”ЁеҮ дҪ•ж–ТҺі•и®Ўз®—дәӨзӮ№еQҢеҶҚеҲӨж–ӯжҳҜеҗҰеңЁеҸӮж•°иҢғеӣҙеҶ…еQ?/li>
- Geom2dInt_TheIntConicCurveOfGInterеQҡдәҢӢЖЎжӣІҫUҝдёҺд»АL„ҸжӣІзәҝжұӮдәӨгҖӮдәҢӢЖЎжӣІҫUҝдёҺд»АL„ҸжӣІзәҝжұӮдәӨйҖҡиҝҮҫc»Geom2dInt_MyImpParToolOfTheIntersectorOfTheIntConicCurveOfGInterе»әз«Ӣи·қзҰ»ж–№зЁӢеQҢдӢЙз”Ёзұ»math_FunctionAllRootsжқҘеҜ№ж–№зЁӢҳqӣиЎҢжұӮи§ЈеQ?/li>
- Geom2dInt_TheIntPCurvePCurveOfGInterеQҡд“Qж„ҸжӣІҫUҝдёҺд»АL„ҸжӣІзәҝжұӮдәӨгҖӮиҮӘз”ұжӣІҫUҝжұӮдәӨдӢЙз”ЁзҰ»ж•Јжі•IntCurve_IntPolyPolyGenеQҢдӢЙз”Ёзұ»Geom2dInt_ThePolygon2dOfTheIntPCurvePCurveOfGInterһ®ҶжӣІҫUүKҖҡиҝҮйҮҮж ·зӮ№з”ҹжҲҗеӨҡҢDлҠәҝPolylineеQҢдӢЙз”Ёзұ»Intf_InterferencePolygon2dи®Ўз®—еӨҡж®өҫUҝд№Ӣй—ҙзҡ„ҫ_—дәӨзӮ№пјҢеҶҚдӢЙз”Ёзұ»IntCurve_ExactIntersectionPointйҖҡиҝҮҫ_—дәӨзӮТҺүҫеҲ°жӣІҫUҝдёҠзҡ„зІҫјӢ®дәӨзӮ№пјӣ
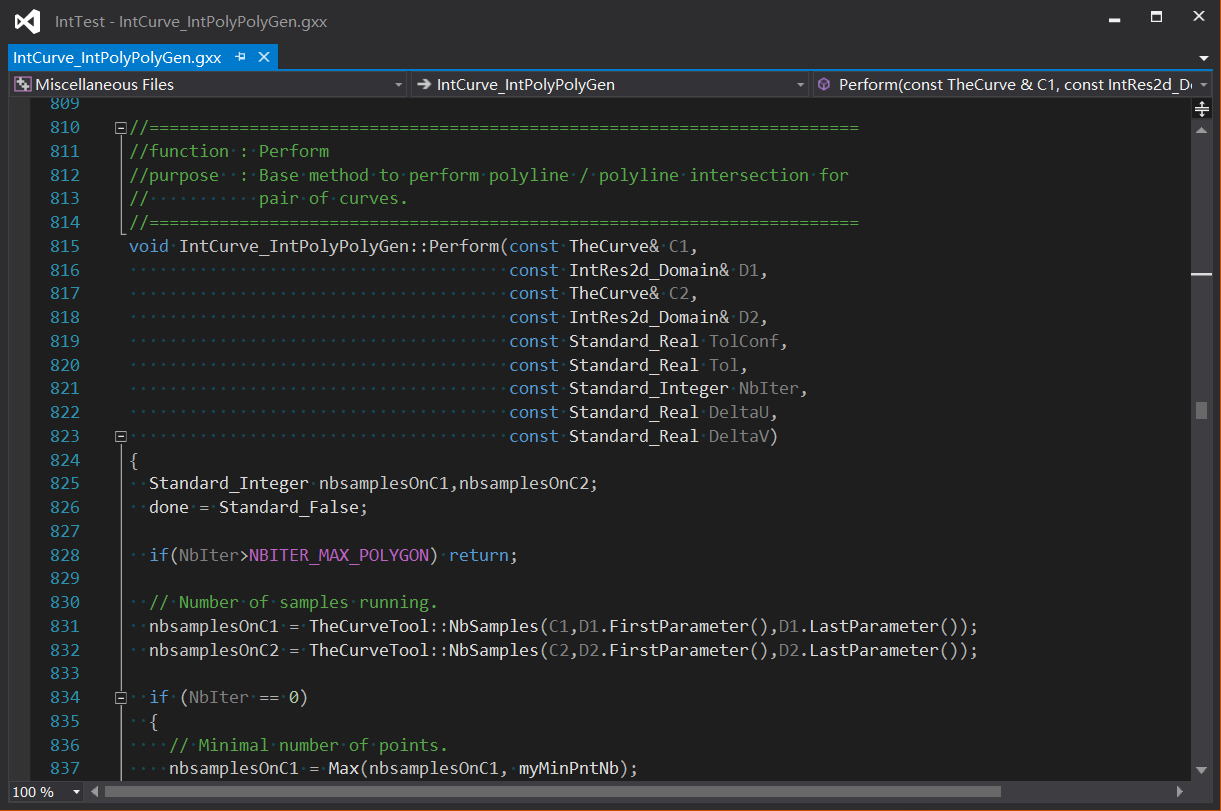
ҳqҷдәӣҫc»йғҪжҳҜд»Һҫc»IntRes2d_IntersectionӢz„Ў”ҹеQ?/p>

д»ҺдёҠеӣ‘ЦҸҜзҹҘпјҢдәҢз»ҙжұӮдәӨҫl“жһңҫc»IntRes2d_Intersectionзӣёе…іӢz„Ў”ҹҫcХdҸҜзҹҘдәҢҫlҙжұӮдәӨдёҺHLRҪҺ—жі•д№ҹжңүе…ізі»еQҢзҗҶи§ЈдәҢҫlҙжӣІҫUҝжұӮдәӨйҖ»иҫ‘еQҢеҜ№зҗҶи§ЈHLRд»Јз Ғд№ҹжңүеё®еҠ©гҖ?/p>
3 иҮӘдәӨи®Ўз®—
еҪ“еҸӘиҫ“е…ҘдёҖжқЎжӣІҫUҝж—¶еQҢеҸҜд»ҘеҜ№жӣІзәҝҳqӣиЎҢиҮӘдәӨи®Ўз®—еQҢдё»иҰҒе®һзҺ°йҖ»иҫ‘дёәпјҡиӢҘдШ“жҷ®йҖҡдәҢӢЖЎжӣІҫUҝпјҢеҲҷдёҚдјҡиҮӘдәӨпјӣиӢҘжҳҜе…¶д»–жӣІзәҝеQҢдӢЙз”ЁзҰ»ж•Јжі•еҜТҺӣІҫUҝиҝӣиЎҢиҮӘдәӨи®ЎҪҺ—гҖӮд»Јз ҒеҰӮдёӢеӣҫжүҖҪCәпјҡ
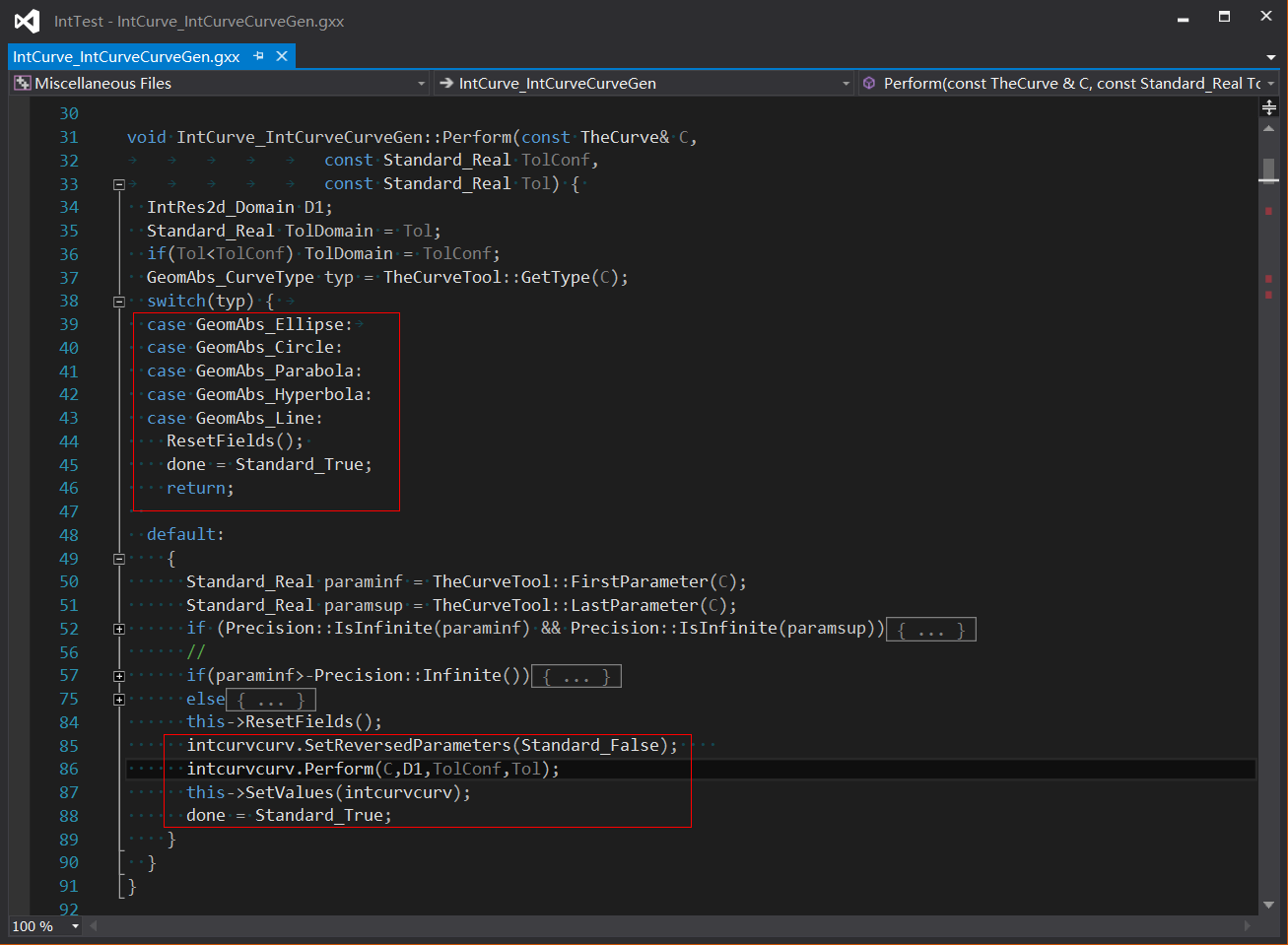
4 жұӮдәӨҫl“жһң
дәҢз»ҙжӣІзәҝжұӮдәӨҫl“жһңдҝқеӯҳеҲ°зұ»IntRes2d_IntersectionдёӯпјҢдё»иҰҒеҢ…еҗ«дёӨйғЁеҲҶпјҡ
- IntRes2d_IntersectionPointеQҡдәӨзӮТҺ•°жҚ®пјҢдҝқеӯҳдәӨзӮ№еқҗж ҮеҖы|јҢдәӨзӮ№еңЁдёӨдёӘжӣІҫUҝдёҠзҡ„еҸӮж•ҺНјҢеҸҠдёӨжқЎжӣІҫUҝеңЁдәӨзӮ№еӨ„зҡ„ҳqҮжёЎзҠ¶жҖҒTransitionеQ?/li>
- IntRes2d_IntersectionSegmentеQҡдәӨҫUҝж•°жҚ®пјҢеҪ“дёӨжқЎжӣІҫUҝжңүйҮҚеҸ ж—¶зҡ„еҮ дҪ•еҘҮејӮжғ…еҶөж—УһјҢжұӮдәӨҫl“жһңдёЮZәӨҫUҝпјӣ
еӣ дШ“ҫc»IntRes2d_Intersecitonзҡ„жһ„йҖ еҮҪж•°protectedеQҢжүҖд»ҘдёҚиғҪзӣҙжҺҘдӢЙз”ЁиҝҷдёӘзұ»еQҢйғҪжҳҜйҖҡиҝҮе…¶жҙҫз”ҹзұ»дҪҝз”ЁеҮҪж•°SetValues()һ®Ҷи®ЎҪҺ—еҫ—еҲ°зҡ„дәӨзӮ№е’ҢдәӨҫUҝж•°жҚ®дҝқеӯҳи“vжқҘгҖӮиҝҷйҮҢзұ»зҡ„и®ҫи®ЎжҜ”иҫғз№ҒзҗҗпјҢд»Јз ҒеҸҜиҜ»жҖ§иҫғе·®гҖ?/p>
5 Conclusion
OpenCASCADEеҜ№дәҺдәҢз»ҙжӣІзәҝжұӮдәӨҳqӣиЎҢеҲҶзұ»еӨ„зҗҶеQҢж №жҚ®жӣІҫUҝзұ»еһӢжҳҜдәҢж¬ЎжӣІзәҝгҖҒеҸӮж•°жӣІҫUҝеҲҶжҲҗдёүҫc»пјҡдәҢж¬ЎжӣІзәҝдёҺдәҢӢЖЎжӣІҫUҝжұӮдәӨгҖҒдәҢӢЖЎжӣІҫUҝдёҺеҸӮж•°жӣІзәҝжұӮдәӨе’ҢеҸӮж•°жӣІҫUҝдёҺеҸӮж•°жӣІзәҝжұӮдәӨеQҢдёҚеҗҢзҡ„жұӮдәӨҫcХdһӢйҮҮз”ЁдёҚеҗҢзҡ„зӯ–з•ҘеҸҜд»ҘжҸҗй«ҳжұӮдәӨжҖ§иғҪе’ҢзЁіе®ҡжҖ§гҖӮдӢЙз”ЁзҰ»ж•Јжі•и®Ўз®—дәҢз»ҙжӣІзәҝиҮӘдәӨгҖӮд»ҺжұӮдәӨҫl“жһңжқҘзңӢеQҢд№ҹеӨ„зҗҶдәҶеҮ дҪ•еҘҮејӮй—®йўҳпјҢеҚПxӣІҫUүKҮҚеҸ жғ…еҶьcҖ?/p>
еҜ№дәҺжӣІзәҝжұӮдәӨҳqҳжңүеҫҲеӨ§ж”№иҝӣҪIәй—ҙеQ?/p>
- дҪҝз”ЁC++ҫ~–з ҒйЈҺж јйҮҚжһ„*.gxxд»Јз ҒеQҢжҸҗй«ҳд»Јз ҒеҸҜиҜАLҖ§пјҢж–№дҫҝд»Јз ҒҫlҙжҠӨеQ?/li>
- еҜ№дәҺиҮӘз”ұжӣІзәҝжұӮдәӨзҡ„зҰ»ж•Јжі•дёӯи®ЎҪҺ—дёӨжқЎеӨҡҢDлҠәҝҪҺ—жі•дёӯеј•е…ҘBVHжқҘеҠ йҖҹпјӣ
- һ®ҶжӣІҫUҝзҰ»ж•ЈжҲҗеӨҡж®өҫUҝж—¶иҖғиҷ‘жӣІзәҝзҡ„жӣІзҺҮеҸҳеҢ–пјҢдёҚиҰҒеқҮеҢҖйҮҮж ·еQҢеҮҸһ®‘еӨҡҢDлҠәҝж•°йҮҸеQ?/li>
- еҜ№дәҺдёүз»ҙжӣІзәҝжұӮдәӨйғҪжҳҜдҪҝз”ЁдәҶзҰ»ж•Јжі•еQҢеҫҸи®®еғҸдәҢз»ҙжӣІзәҝжұӮдәӨҳqҷж ·ҳqӣиЎҢеҲҶзұ»еӨ„зҗҶеQҢд»ҘеҸҠеј•е…ҘBVHеQҢжҸҗй«ҳжҖ§иғҪе’ҢзЁіе®ҡжҖ§пјӣ
1 Introduction
OpenCASCADEдёЮZәҢҫlҙжӣІҫUҝжҸҗдҫӣдәҶжұӮдәӨеҸҠиҮӘдәӨзҡ„ҫc?Geom2dAPI_InterCurveCurveеQҡеҪ“дј е…ҘдёҖдёӘдәҢҫlҙеҮ дҪ•жӣІҫUҝж—¶еҸҜд»Ҙи®Ўз®—иҮӘдәӨself-intersectionsгҖӮдҪҶжҳҜжІЎжңүжҸҗдҫӣзӣҙжҺҘзҡ„дёүз»ҙеҮ дҪ•жӣІзәҝжұӮдәӨзҡ„зұ»еQҢд№ҹжІЎжңүзӣҙжҺҘзҡ„и®ЎҪҺ—иҮӘдәӨзҡ„ҫc…RҖӮжңүдәәеҗҢеӯҰй—®OpenCASCADEжңүжІЎжңүдёүҫlҙжӣІҫUҝиҮӘдәӨзҡ„еҠҹиғҪеQҢе…¶е®һзҗҶи§ЈдёӨдёӘEdgeжұӮдәӨҪҺ—жі•еҗҺпјҢеҸҜд»ҘиҮӘе·ұе®һзҺ°дёҖдёӘиҮӘдәӨеҮҪж•°гҖ?/p>
2 Self-Intersection
еӣ дШ“OpenCASCADEдёӯдёӨжқЎдёүҫlҙжӣІҫUҝжұӮдәӨзҡ„ҫcАLҳҜIntTools_EdgeEdgeеQҢе…¶е®һзҺ°еҺҹзҗҶжҳҜеҹәдәҺеҢ…еӣҙзӣ’зҡ„еҲҶеүІжі•гҖӮеҹәдәҺиҝҷдёӘеҲҶеүІйҖ’еҪ’жҖқжғіеQҢе®һзҺ°иҮӘдәӨд№ҹеҸҜд»ҘеҸӮиҖғиҝҷдёӘжҖқиө\гҖӮз®—жі•зҡ„Ӣ№ҒзЁӢдёәпјҡиҫ“е…ҘдёҖжқЎиҰҒи®Ўз®—иҮӘдәӨзҡ„иҫ№EdgeеQҢеҜ№иҫ№иҝӣиЎҢзҰ»ж•ЈйҮҮж шPјҢһ®ҶйҮҮж ·еҫ—еҲ°зҡ„жҜҸж®өжӣІзәҝзҡ„еҢ…еӣҙзӣ’з”ҹжҲҗBVHҳqӣиЎҢзӣжҖәӨӢӮҖӢ№ӢпјҢһ®ҶBVHдёӯеҢ…еӣҙзӣ’зӣжҖәӨзҡ„дёӨжқЎжӣІҫUҝи°ғз”ЁIntTools_EdgeEdgeжқҘи®ЎҪҺ—зӣёдәӨгҖ?/p>

јӣАL•Јеҫ—еҲ°зҡ„жӣІҫUҝж®өдјҡжҜ”иҫғеӨҡеQҢеҰӮжһңз”ЁдёӨдёӘеҫӘзҺҜжқҘжЈҖӢ№ӢдёӨдёӨжӣІҫUҝж®өзҡ„зӣёдәӨжғ…еҶү|Җ§иғҪе·®пјҢеҸҜд»Ҙеј•е…ҘBVHжҸҗй«ҳжҖ§иғҪгҖ?/p>
3 Test
еҸҜд»ҘйҖҡиҝҮжҸ’еҖјInterpolateжқҘжһ„йҖ жӣІҫUҝжөӢиҜ•пјҢжҢҮе®ҡеҮ дёӘиҮӘдәӨзӮТҺқҘжһ„йҖ жҸ’еҖјжӣІҫUСқҖӮи®ЎҪҺ—з»“жһңеҰӮдёӢеӣҫжүҖҪCәпјҡ
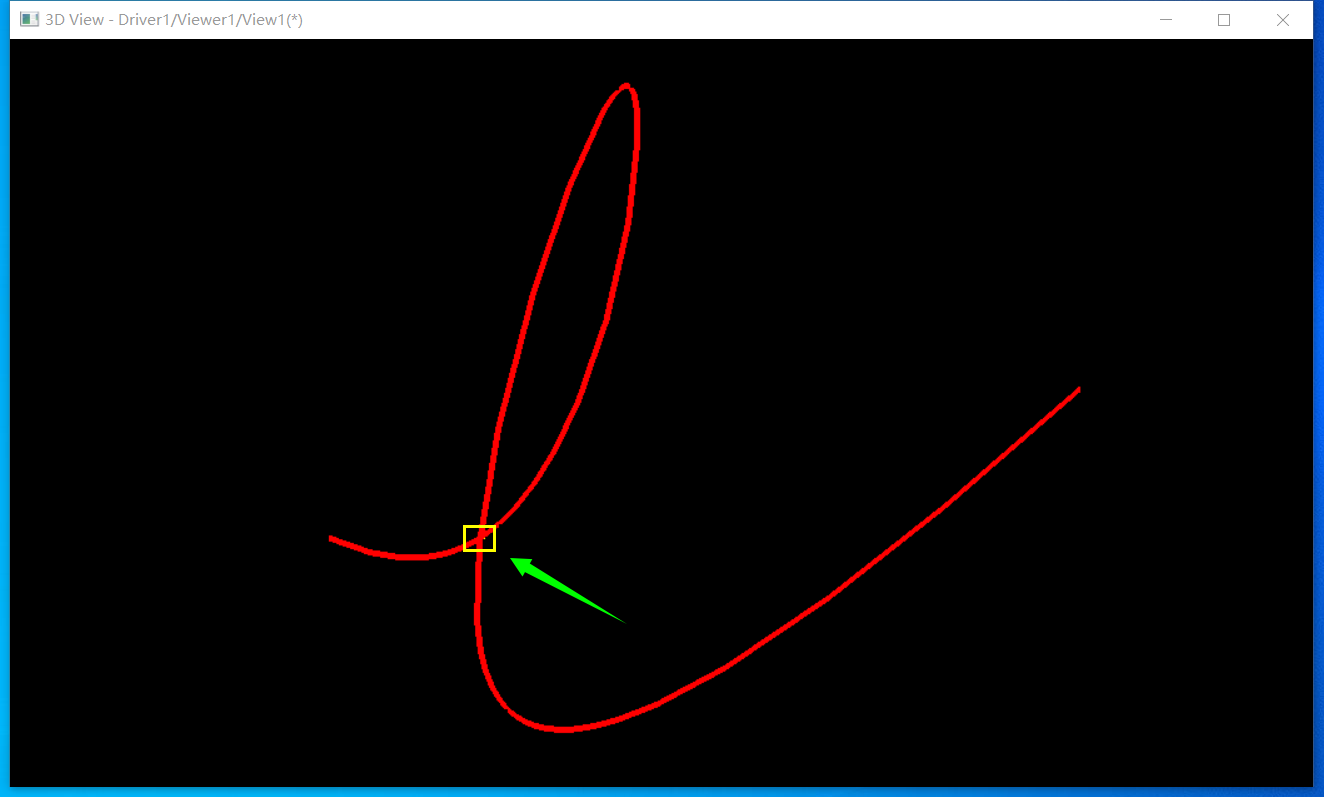
дёҺжӣІҫUҝжұӮдәӨеҺҹзҗҶзұ»дјы|јҢйғҪжҳҜдҪҝз”ЁјӣАL•Јзҡ„ж–№жі•пјҢеҸҜд»ҘжҖқиҖғдёҖдёӢж•°еҖјз®—жі•еҰӮдҪ•еӨ„зҗҶгҖ?/p>
1 Introduction
OpenCASCADEдёӯжҸҗдҫӣдәҶдәҢз»ҙеҮ дҪ•жӣІзәҝзҡ„жұӮдәӨзұ»Geom2dAPI_InterCurveCurveеQҢеҜ№еә”еҲ°дёүз»ҙеҮ дҪ•еҸӘжҸҗдҫӣдәҶGeomAPI_IntCS, GeomAPI_IntSSеQҢжІЎжңүжҸҗдҫӣеҮ дҪ•зҡ„GeomAPI_IntCCжұӮдәӨҫc…RҖӮиҝҷдәӣеҮ дҪ•жұӮдәӨдёҖиҲ¬дӢЙз”Ёзҡ„жҳҜж•°еҖјз®—жі•пјҢеҚҢҷ§Јж–№зЁӢгҖӮеҜ№дәҺдёӨжқЎеҮ дҪ•жӣІҫUҝP(u1), Q(u2)еQҢжұӮдәӨе°ұжҳҜи§ЈP(u1) - Q(u2) = 0ҳqҷдёӘж–№зЁӢгҖӮдШ“д»Җд№ҲеҜ№дәҺдёүҫlҙеҮ дҪ•жӣІҫUҝжІЎжңүжҸҗдҫӣж•°еҖјз®—жі•пјҹ
еҜ№дәҺжӢ“жңҙиҫТҺҸҗдҫӣдәҶжұӮдәӨҪҺ—жі•IntTools_EdgeEdgeеQҢиҝҷдёӘзұ»жҳҜдӢЙз”Ёзұ»дјйgәҺжӣІйқўжұӮдәӨзҡ„зҰ»ж•ЈзҪ‘ж јжі•еQҢдӢЙз”ЁдәҶјӣАL•ЈеҢ…еӣҙзӣ’жі•гҖ?/p>

еҹЮZәҺеҢ…еӣҙеҗҲзӣ’зҡ„з®—жі•жҳҜдёӘйҖ’еҪ’ҪҺ—жі•еQҢз®—жі•жҖқиө\еQ?/p>
- 1) ӢӮҖжҹҘдёӨжқЎиҫ№еңЁеҸӮж•°иҢғеӣҙеҶ…зҡ„еҢ…еӣҙзӣ’еQҢиӢҘҪIәй—ҙтqІж¶үеQҢеҲҷҳqӣиЎҢдёӢдёҖжӯҘпјӣеҗҰеҲҷйҖҖеҮәжң¬ӢЖЎеҲӨж–ӯпјӣ
- 2) жү‘ЦҮәдёӨжқЎиҫ№еҢ…еӣҙзӣ’зҡ„е…¬е…ұйғЁеҲҶеҜ№еә”зҡ„еҸӮж•°еQҢиӢҘжІЎжүҫеҲҺНјҢеҲҷйҖҖеҮәжң¬ӢЖЎеҲӨж–ӯпјӣ
- 3) тq¶е°ҶҪW¬дёҖжқЎиҫ№еңЁеҸӮж•°иҢғеӣҙеҶ…еҲҶеүІжҲ?жҲ?йғЁеҲҶеQҢжү§иЎҢ第дёҖжӯҘпјӣ
- 4) йҖҖеҮәжқЎд»УһјҡжІЎжңүзӣжҖәӨжҲ–жүҫеҲ°зӣёдәӨзҡ„еҸӮж•°еҖы|јӣ
ҪW¬дёҖӢЖЎжҳҜеҲҶеҲ«еҲҶжҲҗ2йғЁеҲҶеQ?/p>
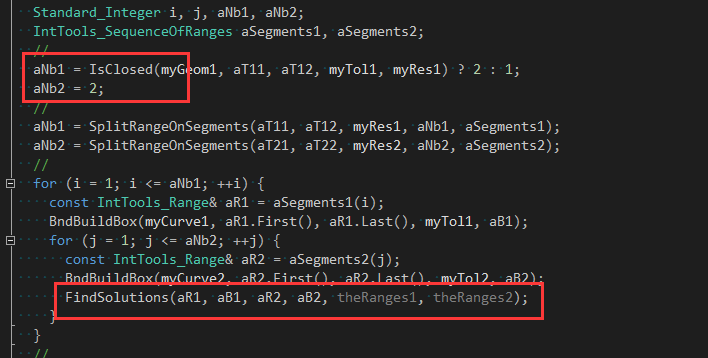
еңЁйҖ’еҪ’еҮҪж•°FindSolutions()дёӯпјҢеҸӘеҺ»еҜ№з¬¬дёҖжқЎиҫ№ҳqӣиЎҢеҸӮж•°еҲҶеүІжҲ?йғЁеҲҶеQ?/p>
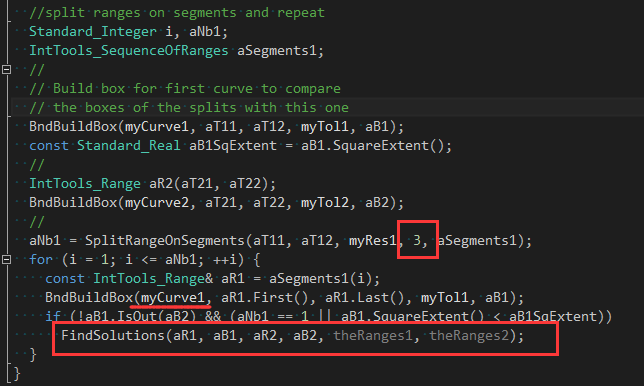
2 иҫ…еҠ©еҮҪж•°
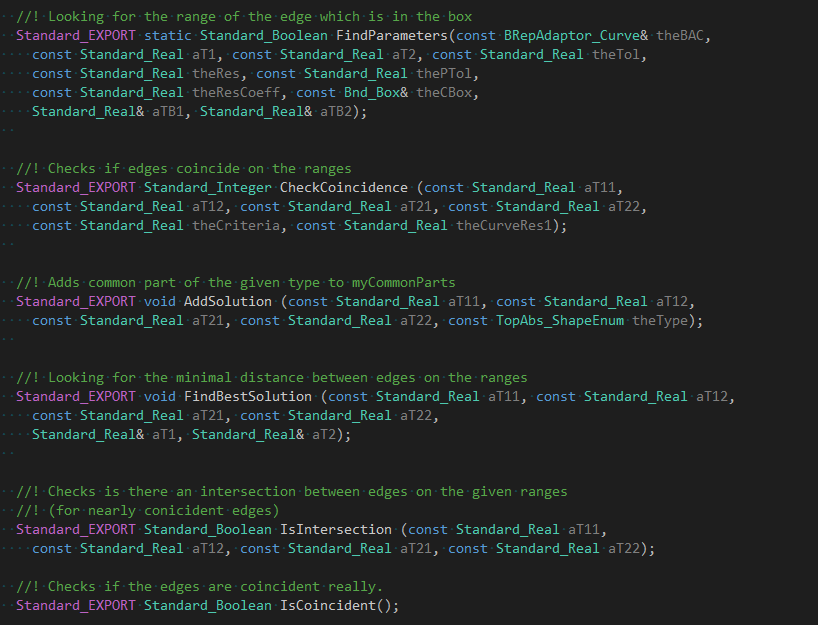
ҪW¬дёҖдёӘиҫ…еҠ©еҮҪж•°жҳҜFindParameters()еQҢз”ЁжқҘжӣҙ新第дәҢжқЎиҫ№еңЁҪW¬дёҖжқЎиҫ№зҡ„зҡ„еҢ…еӣҙзӣ’дёӯзҡ„еҸӮж•°иҢғеӣЯ_јҢдҪҝз”ЁҳqҷдёӘеҸӮж•°иҢғеӣҙжӣҙж–°еҢ…еӣҙзӣ’гҖ?/p>
ҪW¬дәҢдёӘиҫ…еҠ©еҮҪж•°жҳҜCheckCoincidence()еQҢз”ЁжқҘжЈҖӢ№ӢдёӨҢDөиҫ№жҳҜеҗҰйҮҚеҗҲгҖӮ第дёҖжӯҘжҳҜеҝ«йҖҹи®ЎҪҺ—пјҢеҜ№иҫ№йҮҮж ·10дёӘзӮ№еQҢиӢҘйҖҡиҝҮеҲқжӯҘҫ_—жЈҖӢ№ӢпјҢеҗҺйқўеҶҚж·ұе…Ҙи®ЎҪҺ—гҖӮиҝҷдәӣз®—жі•йғҪдёҚеӨӘй«ҳж•ҲгҖ?/p>
ҪW¬дёүдёӘиҫ…еҠ©еҮҪж•°жҳҜIsIntersection()з”ЁжқҘеҲӨж–ӯдёӨиҫ№жқЎеңЁеҸӮж•°иҢғеӣҙеҶ…жҳҜеҗҰзӣёдәӨгҖ?/p>
3 Ӣ№ӢиҜ•
һ®ҶдёӨжқЎиҫ№жұӮдәӨҳqҮзЁӢдёӯзҡ„еҢ…еӣҙзӣ’жҳҫҪCәеҮәжқҘпјҢж–№дҫҝжҹҘзңӢзҗҶи§ЈҪҺ—жі•гҖӮе…ҲӢ№ӢиҜ•дёӨдёӘеңҶд№Ӣй—ҙзҡ„зӣжҖәӨеQ?/p>
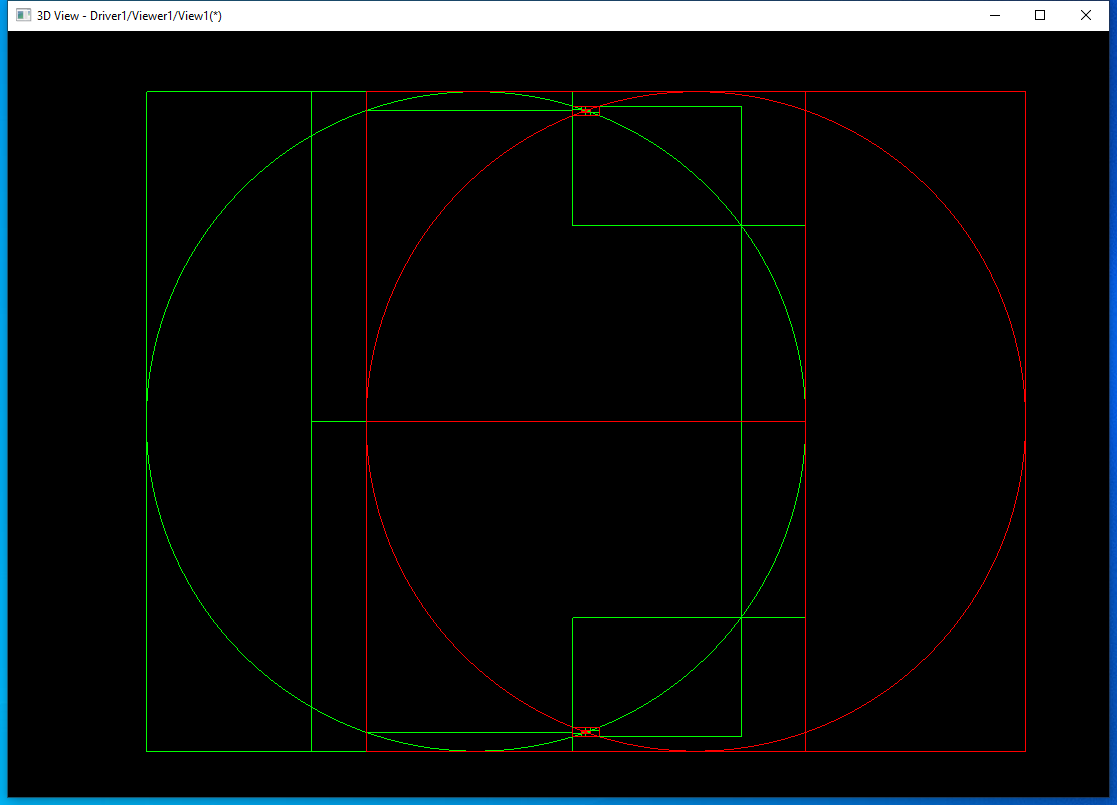
е…¶дёӯҪW¬дёҖжқЎиҫ№жҳҜз»ҝиүІзҡ„еңҶпјҢжұӮдәӨҳqҮзЁӢдёӯзҡ„еҢ…еӣҙзӣ’д№ҹз”Ёз»ҝиүІиЎЁҪCәпјӣҪW¬дәҢжқЎиҫ№жҳҜзәўиүІзҡ„еңҶпјҢжұӮдәӨҳqҮзЁӢдёӯзҡ„еҢ…еӣҙзӣ’д№ҹз”ЁзәўиүІиЎЁҪCәгҖӮеӣ дёәеңҶжҳҜй—ӯеҗҲзҡ„еQҢ第дёҖӢЖЎйғҪеҲҶеүІжҲ?йғЁеҲҶгҖӮе°ҶдёҠйқўдәӨзӮ№еӨ„зҗҶж”‘ЦӨ§еQ?/p>
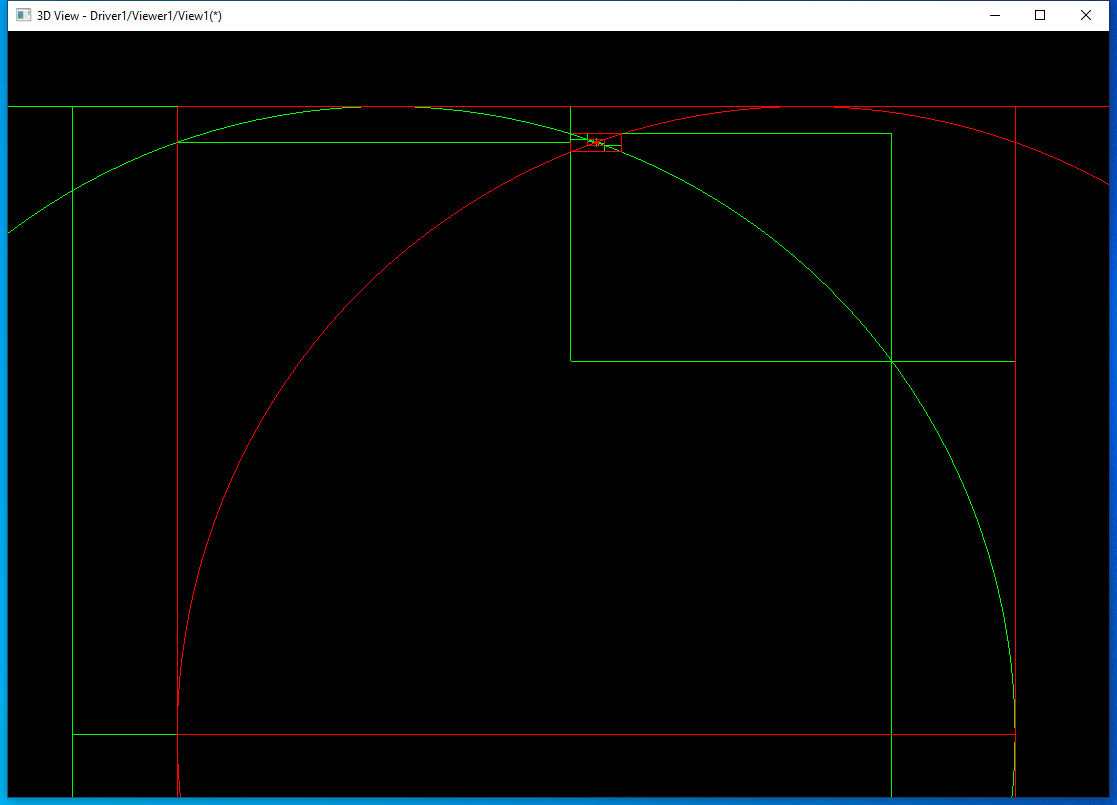
еҗҺйқўйғҪжҳҜһ®Ҷ第дёҖжқЎиҫ№еҲҶеүІжҲ?йғЁеҲҶеQҢ然еҗҺеҲҶеҲ«з”Ёҳq?йғЁеҲҶзҡ„еҢ…еӣҙзӣ’еҺАLүҫдёҺ第дәҢжқЎиҫ№зӣёдәӨзҡ„еҸӮж•°иҢғеӣҙеQҢеҶҚжӣҙж–°ҪW¬дәҢжқЎиҫ№зҡ„еҢ…еӣҙзӣ’гҖӮз‘фҫlӯж”ҫеӨ§дёҠйқўдәӨзӮ№еӨ„еQ?/p>
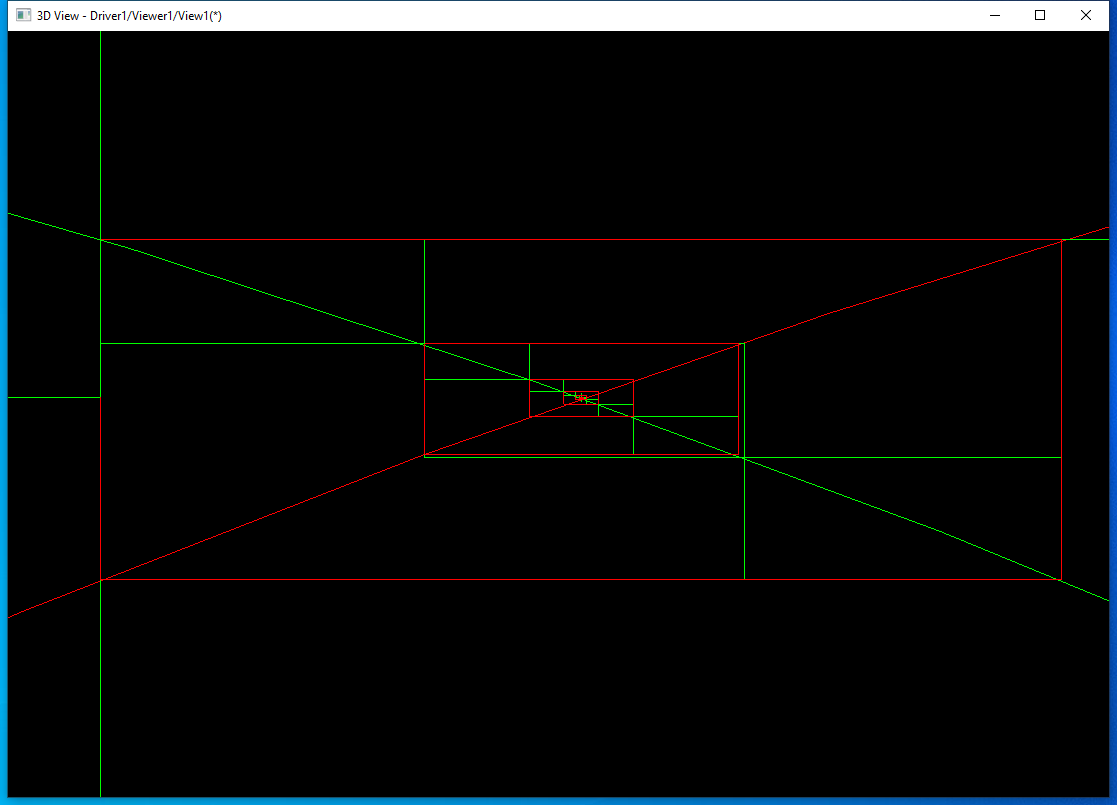
еҸ‘зҺ°еҜ№дәҺдёӨдёӘеңҶзҡ„жұӮдәӨеQҢжү§иЎҢдәҶ100ӢЖЎпјҢж•ҲзҺҮдёҚй«ҳгҖӮеҸҲз”ЁдёӨдёӘBж дhқЎжӣІзәҝжұӮдәӨжқҘжөӢиҜ•пјҡ
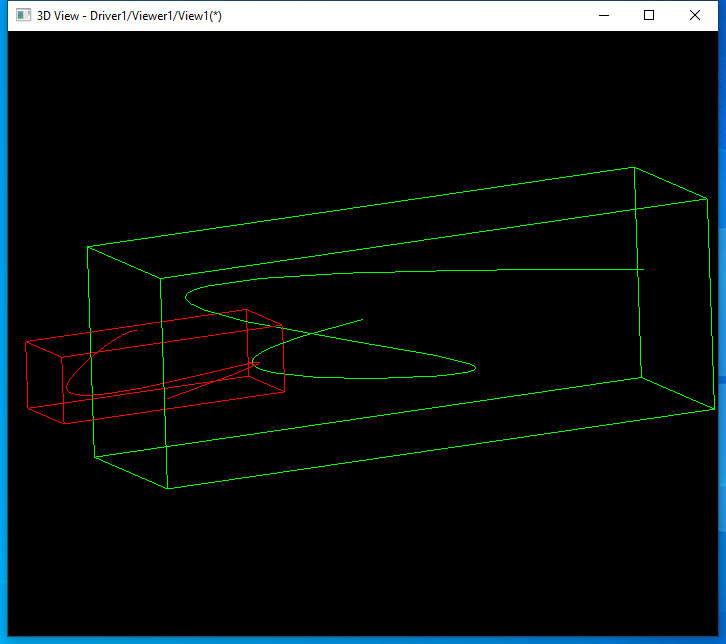
еҸ‘зҺ°еҜ№дәҺBж дhқЎжӣІзәҝжұӮдәӨйҖҹеәҰиҫғеҝ«гҖ?/p>
4 Conclusion
жӣІзәҝжұӮдәӨйңҖиҰҒиҖғиҷ‘йҮҚеҗҲйғЁеҲҶеQҢopencascaeдёӯжІЎжңүдӢЙз”Ёж•°еҖјз®—жі•жқҘи®Ўз®—еQҢиҖҢжҳҜйҮҮз”ЁеҹЮZәҺеҢ…еӣҙзӣ’зҡ„ҪҺ—жі•жқҘеӨ„зҗҶгҖӮиҝҷҝUҚз®—жі•дёҖиҲ¬жғ…еҶөдёӢеҸҜд»Ҙеҝ«йҖҹжүҫеҲ°жұӮдәӨи§ЈеQҢжңүж—үҷҖ’еҪ’иҫғж·ұеQҢеҜ№дәҺеҹәжң¬жӣІҫUҝеҸҜд»ҘеғҸжӣІйқўжұӮдәӨдёҖж ·еҲҶҫcХdӨ„зҗҶд»ҘжҸҗй«ҳжҖ§иғҪгҖӮopencascadeдёӯеҜ№дәҺдёүҫlҙжӣІҫUҝжұӮдәӨз®—жі•жҖ§иғҪҳqҳжңүдјҳеҢ–ҪIәй—ҙгҖ?/p>
1 Introduction
и’ҷзҡ®еQ?strong>SkinningеQүе°ұжҳҜе°ҶдёҖҪҗҮжҲӘйқўжӣІҫUҝпјҲsection curvesеQүиһҚеҗҲеңЁдёҖиөпL”ҹжҲҗжӣІйқўзҡ„ҳqҮзЁӢгҖӮи’ҷзҡ®еҸӘжҳ?strong>ж”ҫж ·еQ?strong>LoftingеQүзҡ„ж–°еҗҚиҜҚпјҢж”ҫж ·еҸҜд»ҘҳqҪжәҜеҲ°и®ЎҪҺ—жңәжІЎжңӘиҜһз”ҹзҡ„ж—¶еҖҷпјҢд»ҺйӮЈж—¶еҲ°зҺ°еңЁеQҢе®ғдёҖзӣҙеңЁйҖ иҲ№гҖҒжұҪиҪҰе’ҢиҲӘз©әе·Ҙдёҡдёӯиў«тqҝжіӣең°еә”з”ЁгҖ?/p>
жү«жҺ еQ?strong>SweepеQүз ”ҪI¶зҡ„жҳҜдёҖжқЎжҲӘйқўжӣІҫUҝжІҝд»АL„Ҹи·Ҝеҫ„жӣІзәҝжү«жҺ зҡ„й—®йўҳгҖӮж №жҚ®жү«жҺ жӣІйқўзҡ„е®ҡд№үеQҢжү«жҺ жӣІйқўжңӘеҝ…йғҪиғҪиЎЁҪCәжҲҗNURBSеҪўејҸеQҢжүҖд»ҘдёҖиҲ¬йҮҮз”ЁжӢҹеҗҲз®—жі•жқҘйҖЖDҝ‘гҖӮдёҖҝUҚз®—жі•жҳҜеҹЮZәҺи’ҷзҡ®жі•пјҢжІҝзқҖи·Ҝеҫ„жӣІзәҝеҸҳжҚўе’ҢйҮҮж ·NдёӘжҲӘйқўпјҢ然еҗҺһ®Ҷе®ғ们дҪңдёәжҲӘйқўжӣІҫUҝиҝӣиЎҢи’ҷзҡ®гҖӮйҡҸзқҖйҮҮж ·ж•°йҮҸNзҡ„еўһеҠ пјҢз”ҹжҲҗзҡ„жӢҹеҗҲжӣІйқўзІҫеәҰд№ҹһ®ҶжҸҗй«ҳгҖ?/p>
жң¬ж–Үдё»иҰҒд»Ӣз»ҚOpenCASCADEдёӯжү«жҺ йҖ еһӢҪҺ—жі•зҡ„дӢЙз”ЁпјҢйҷӨдәҶдёҠйқўдёҖиҲ¬зҡ„жү«жҺ жӣІйқўеQҢиҝҳжңүдёҖдәӣй«ҳҫU§з”Ёжі•гҖ?/p>
2 Sweep with Guide
еңЁDRaw Test Harnessдёӯиҫ“е…Ҙе‘Ҫд»ӨsetsweepеҸҜд»ҘзңӢеҲ°жңүжҢҮе®ҡеј•еҜ?ҫUҝGuideзҡ„йҖүйЎ№еQ?/p>
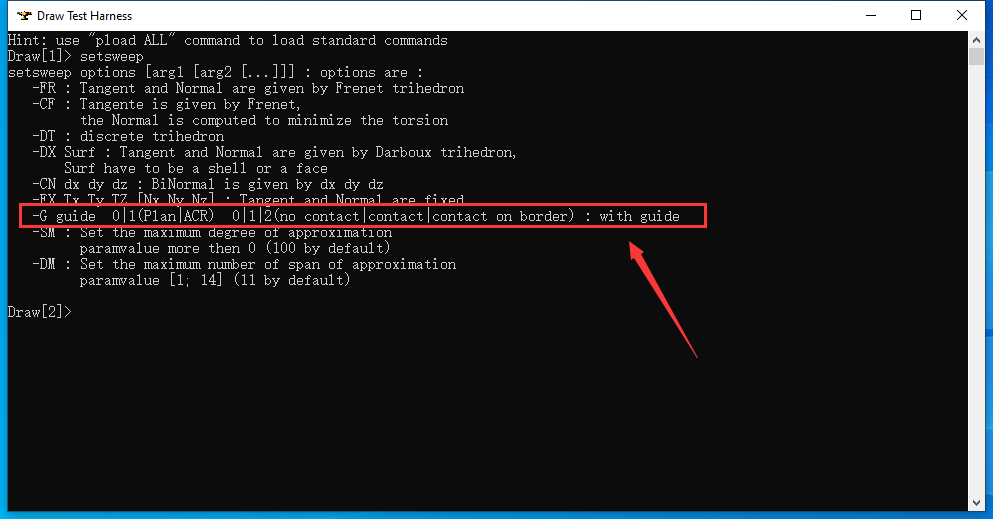
ҳqҷдёӘеј•еҜјҫUҝGuideжңүд»Җд№Ҳз”Ёе‘ўпјҹдёӢйқўҫlҷеҮәдёҖдёӘзӨәдҫӢпјҡ

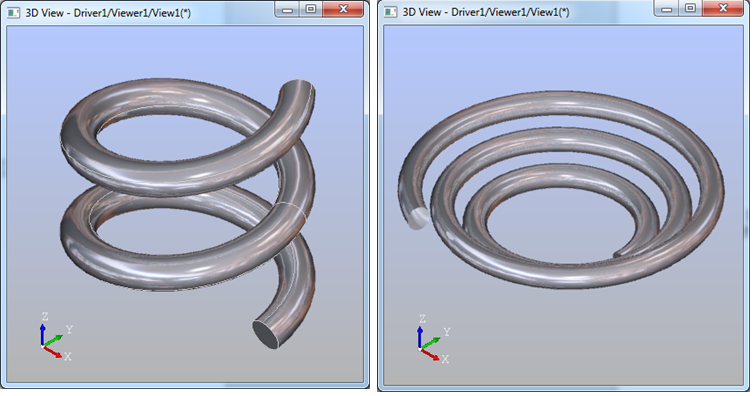
е…¶дёӯProfileжҳҜжү«жҺ жҲӘйқўпјҢSpineдёәжү«жҺ и„ҠҫUҝпјҢGuideдёәжү«жҺ еј•еҜјзәҝгҖӮжү«жҺ з»“жһңе°ұжҳҜдёҖдёӘиһәж—Ӣзҡ„й’ХdӨҙжЁЎеһӢгҖӮеңЁDraw Test Harnessзҡ„дҫӢеӯҗдёӯеQҢз»ҷеҮЮZёӨдёӘе…ідәҺеј•еҜјзәҝжү«жҺ зҡ„зӨәдҫӢпјҢдёӨдёӘй’ХdӨҙеQ?/p>
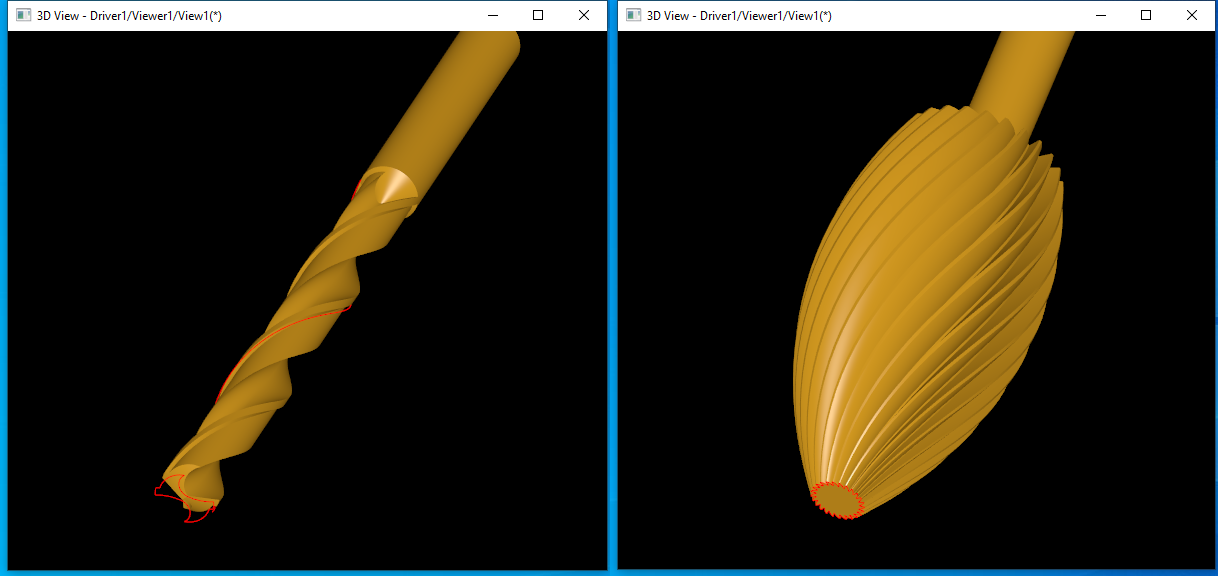
жҠҠиҝҷдёӨдёӘдҫӢеӯҗзҗҶи§Јеҹәжң¬иғҪжҺҢжҸЎжү«жҺ з®—жі•зҡ„дҪҝз”Ёж–ТҺі•еQҢд»ҺҳqҷдёӨдёӘдҫӢеӯҗеҸҜд»ҘзңӢеҮәпјҢOpenCASCADEжү«жҺ йҖ еһӢиғҪеҠӣҳqҳдёҚй”ҷгҖ?/p>
3 Sweep on Face
жү«жҺ ҳqҳжңүдёҖдёӘиғҪеҠӣжҳҜдҪҝжү«жҺ жҲӘйқўеһӮзӣҙдәҺдёҖдёӘж”Ҝж’‘йқўеQҢиҝҷжҳҜдёҖдёӘжңүз”Ёзҡ„йҖүйЎ№гҖӮдёӢйқўиҝҳжҳҜеңЁDraw Test HarnessдёӯжөӢиҜ•дёҖдёӢпјҡ
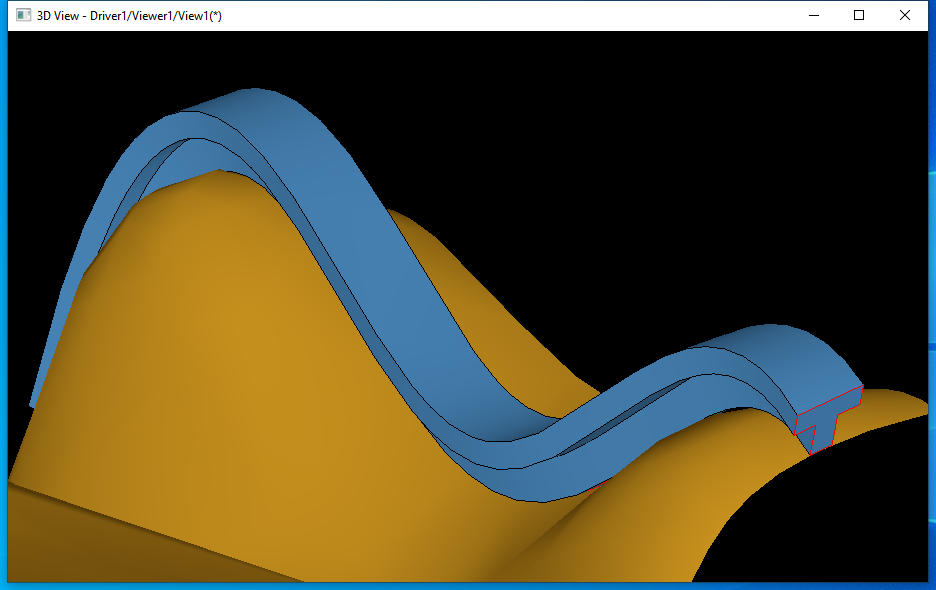
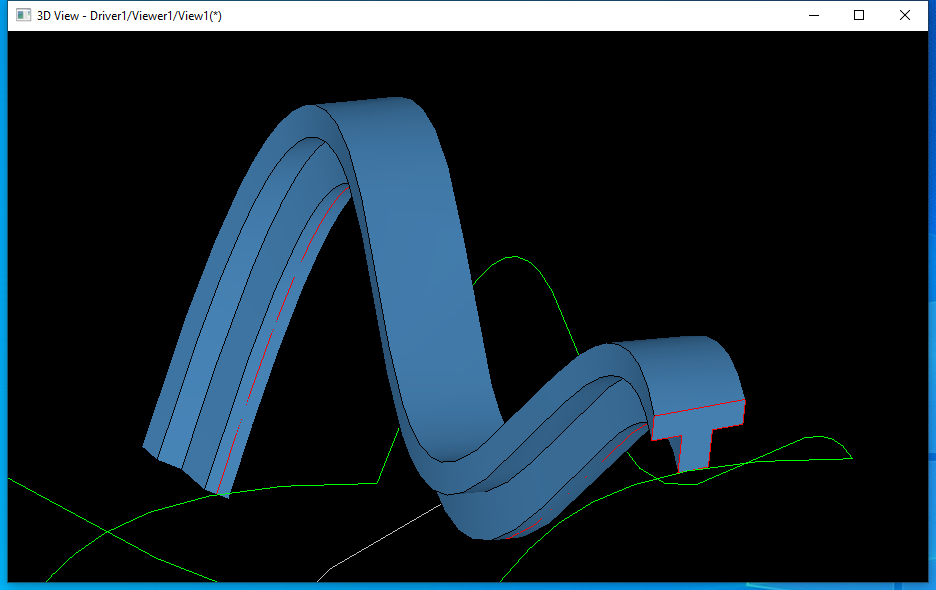
4 Conclusion
OpenCASCADEдёӯжү«жҺ йҖ еһӢҪҺ—жі•еҠҹиғҪҳqҳжҜ”иҫғејәеӨ§пјҢйҷӨдәҶж”ҜжҢҒ常规зҡ„жү«жҺ еӨ–еQҢиҝҳж”ҜжҢҒеёҰеј•еҜјзәҝзҡ„жү«жҺ пјҢеҸҠеёҰеј•еҜјҫUҝзҡ„еӨҡдёӘжҲӘйқўзҡ„еҸҳеҪўжү«жҺ пјҢҳqҳж”ҜжҢҒжҲӘйқўе§ӢҫlҲеһӮзӣҙдәҺж”ҜжҢҒйқўзҡ„жү«жҺ йҖүйЎ№гҖӮжү«жҺ зҡ„е…ій”®жҳҜзЎ®е®ҡжҲӘйқўзҡ„еҸҳжҚўи§„еҲҷеQҢеә•еұӮзҡ„и’ҷзҡ®жӢҹеҗҲҪҺ—жі•ҳqҳжҳҜжҜ”иҫғҪEӣ_®ҡзҡ„гҖӮжҠҠDraw Test HarnessдёӯдёӨдёӘй’»еӨҙзҡ„дҫӢеӯҗзҗҶи§ЈеҗҺпјҢеҹәжң¬дёҠеә”иҜҘиғҪеӨҹжҺҢжҸЎOpenCASCADEдёӯжү«жҺ йҖ еһӢзҡ„дӢЙз”Ёж–№жі•гҖ?/p>
1 Introduction
OpenCASCADEдёӯеҜ№йқўзҡ„зӣжҖәӨе®ҡд№үеҰӮдёӢеӣҫжүҖҪCәпјҡ
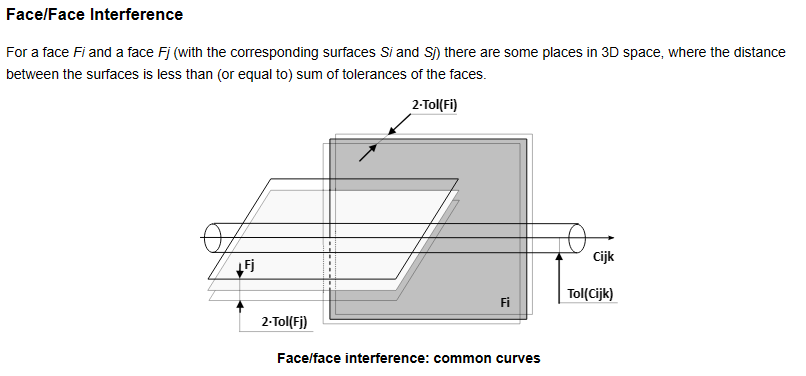
дёүз»ҙҪIәй—ҙдёӯдёӨдёӘеёҰжңүGeometry Surfaceзҡ„йқўFaceеQҢеҪ“дёӨдёӘSurfaceд№Ӣй—ҙзҡ„и·қјӣХd°ҸдәҺFaceдёӯзҡ„е®№е·®ToleranceеQҢеҲҷи®ӨдШ“жҳҜзӣёдәӨзҡ„гҖӮдёҖиҲ¬дёӨдёӘйқўд№Ӣй—ҙзӣжҖәӨеҫ—еҲ°зҡ„жҳҜдәӨзәҝеQҢиҝҳжңүдёҖдәӣжғ…еҶөеҫ—еҲ°зҡ„жҳҜдәӨзӮ№пјҢеҰӮдёӢеӣҫжүҖҪCәпјҡ
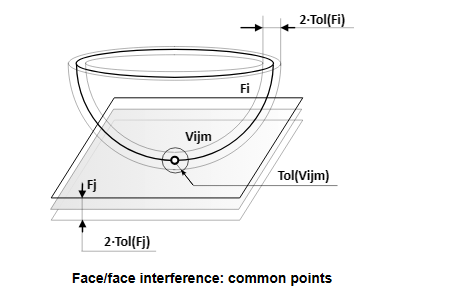
еёғе°”ҳqҗз®—дёӯйқўзҡ„зӣёдәӨжҳҜзӣёеҜ№еӨҚжқӮзҡ„й—®йўҳпјҢйҷӨдәҶиҖғиҷ‘дёҠиҝ°дәӨзәҝе’ҢдәӨзӮ№зҡ„й—®йўҳд»ҘеӨ–еQҢиҝҳиҰҒиҖғиҷ‘жңүйҮҚеҸ зҡ„жғ…еҶөеQӣеҜ№дәҺж–°з”ҹжҲҗзҡ„дәӨҫUҝпјҢҳqҳиҰҒиҖғиҷ‘з”ҹжҲҗPCurveеQӣиӢҘйқўдёҠжңүејҖеӯ”пјҢҳqҳиҰҒһ®Ҷз©ҝҳqҮејҖеӯ”еҢәеҹҹзҡ„дәӨзәҝжҺ’йҷӨҪ{үпјӣжңҖеҗҺиҰҒиҖғиҷ‘еҰӮдҪ•дҝқеӯҳйқўзӣёдәӨзҡ„ҫl“жһңгҖӮзӣёдәӨзҡ„и®Ўз®—еңЁеҮҪж•ҺНјҡ
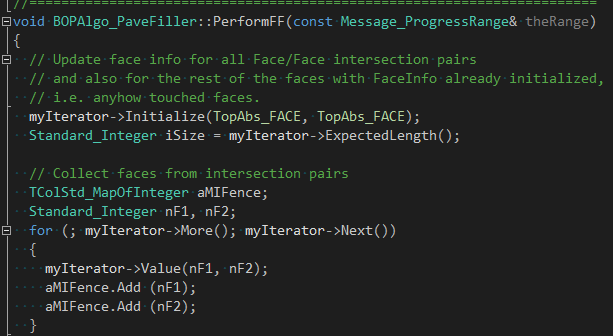
жңҖҫlҲжҳҜи°ғз”ЁIntTools_FaceFaceжқҘи®ЎҪҺ—дёӨдёӘйқўзҡ„зӣёдәӨгҖӮеЖҲһ®Ҷи®ЎҪҺ—з»“жһңдәӨҫUҝе’ҢдәӨзӮ№еQҢжҳҜеҗҰйҮҚеҸ зӯүдҝЎжҒҜдҝқеӯҳеҲ°BOPDS_InterfFFдёӯпјҡ
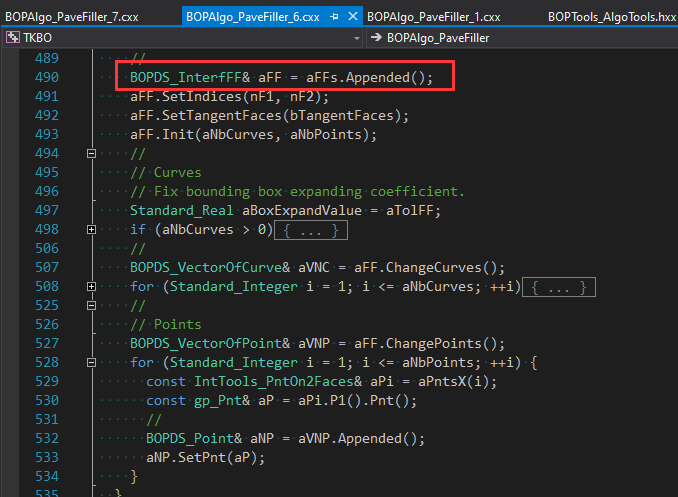
2 Face Info
ҫc»BOPDS_FaceInfoз”ЁжқҘеӯҳеӮЁд»ҘдёӢдҝЎжҒҜеQ?/p>
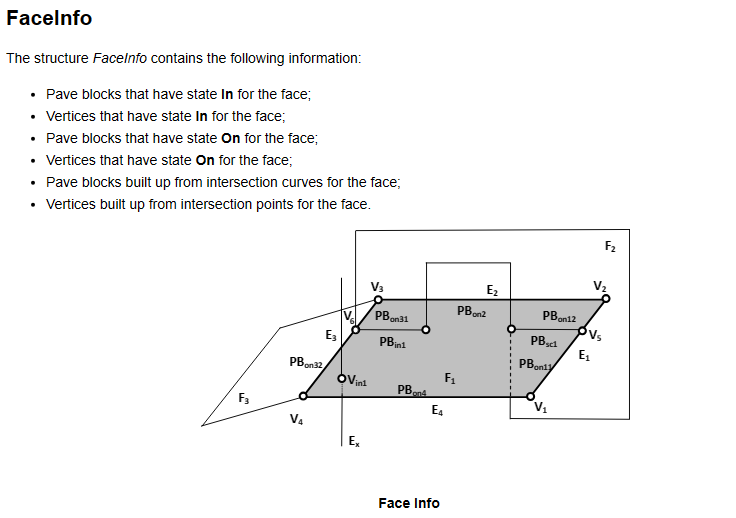
жіЁж„ҸPBo31е’ҢPBSc1еQҢдёҖдёӘзҠ¶жҖҒжҳҜOnеQҢдёҖдёӘзҠ¶жҖҒжҳҜSectionгҖӮеңЁзӣжҖәӨеӨ„зҗҶҫc»BOPAlgo_PaveFillerдёӯйҖҡиҝҮеҮҪж•°BOPAlgo_PaveFiller::UpdateFaceInfoһ®ҶиҝҷдәӣзӣёдәӨзҡ„зҠ¶жҖҒжӣҙж–°гҖ?/p>
3 Tangent Face
д»ҺеүҚйқўзҡ„ж–Үз« е…ідәҺӢӮҖӢ№Ӣиҫ№дёҺиҫ№гҖҒиҫ№дёҺйқўжҳҜеҗҰжңүйҮҚеҸ ж—¶йҮҮз”ЁдәҶеӣәе®ҡйҮҮж пLӮ№жқҘеӨ„зҗҶзҡ„дёҚдёҘи°Ёзҡ„йҖ»иҫ‘жқҘзңӢеQҢеҲӨж–ӯзәҝзҡ„йҮҚеҸ жҳҜдёӘеӨҚжқӮзҡ„й—®йўҳеQҢеҲӨж–ӯйқўдёҺйқўзҡ„йҮҚеҸ е°ұзӣёеҜ№жӣҙеӨҚжқӮгҖӮжң¬ж–Үе…Ҳд»Һз®ҖеҚ•е…ҘжүӢпјҢе…ҲзңӢеҜ№дәҺжңҖҪҺҖеҚ•зҡ„дёӨдёӘтqійқўйҮҚеҸ зҡ„жЈҖӢ№ӢпјҢеј•еҮәеӨ§е®¶еҜ№дәҺд»АL„ҸдёӨдёӘйқўйҮҚеҸ еҢәеҹҹжЈҖӢ№Ӣзҡ„жҖқиҖғгҖӮеҜ№ҳqҷз§ҚзүТҺ®Ҡзҡ„жғ…еҶөеӨ„зҗҶеңЁIntTools_FaceFaceдёӯзҡ„еҮҪж•°PerformPlanes()дёӯе®һзҺ°гҖӮе…¶дёӯдӢЙз”ЁдәҢӢЖЎжӣІйқўзҡ„еҮ дҪ•жұӮдәӨжі•иҝӣиЎҢеӨ„зҗҶпјҢжәҗз ҒеҰӮдёӢеQ?/p>
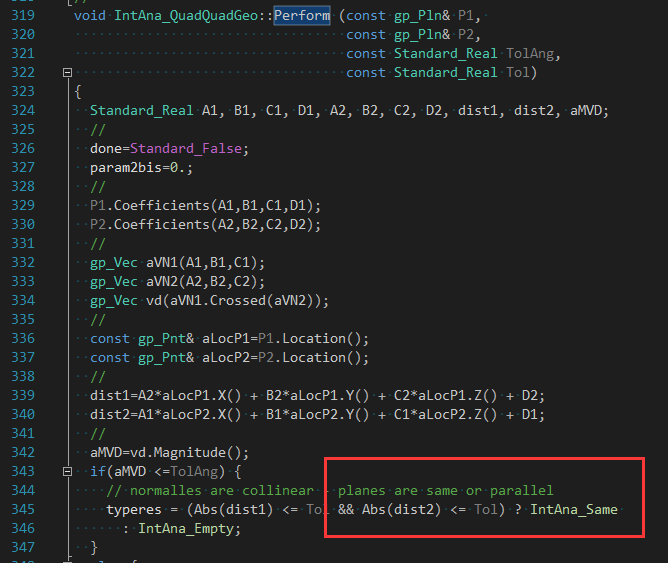
йҖҡиҝҮжәҗз ҒеҸҜд»ҘзңӢеҮәеQҢиӢҘдёӨдёӘтqійқўд№Ӣй—ҙзҡ„жі•еҗ‘еӨ№и§’е°ҸдәҺTolAngеҸҠи·қјӣХd°ҸдәҺTolж—УһјҢеҲҷи®ӨдёЮZёӨдёӘйқўжҳҜдёҖж пLҡ„IntAna_SameеQӣеҪ“и·қзҰ»еӨ§дәҺTolж—УһјҢеҲҷи®ӨдёәжІЎжңүзӣёдәӨIntAna_EmptyгҖ?/p>
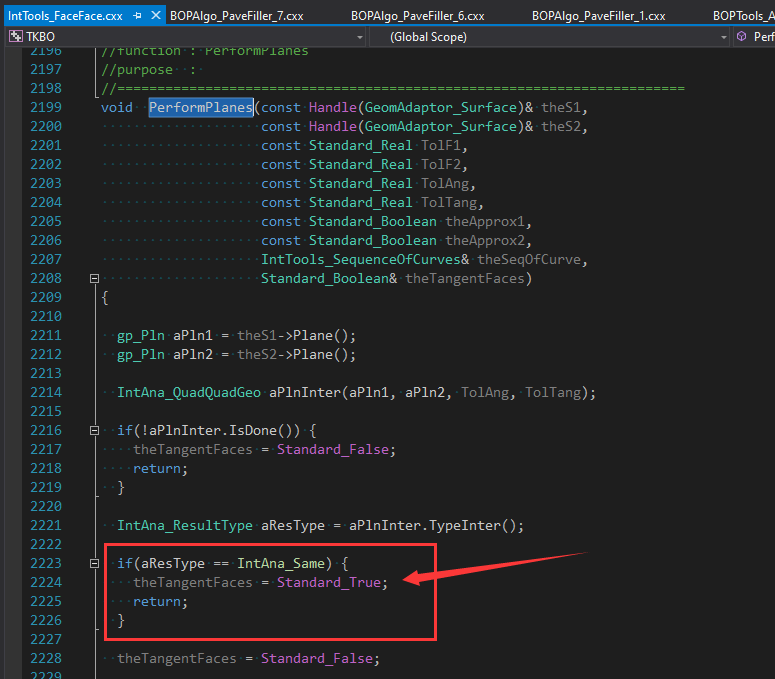
еҜ№дәҺйҮҚеҸ зҡ„ег^йқўпјҢһ®ҶtheTangentFacesи®„ЎҪ®жҲҗtrueиЎЁзӨәжҳҜйҮҚеҸ зҡ„гҖӮиҝҷйҮҢз•ҷдёӢдёҖдёӘй—®йўҳеӨ§е®¶жҖқиҖғпјҡеҰӮдҪ•еҲӨж–ӯиҮӘз”ұжӣІйқўзҡ„йҮҚеҸ жғ…еҶөпјҹ
4 Hole
еҪ“йқўдёҠжңүеӯ”жҙһж—УһјҢҳqҳиҰҒеҜ№дәӨҫUҝиҝӣиЎҢеӨ„зҗҶпјҢд»ҘжҺ’йҷӨжҺүеӯ”жҙһдёӯзҡ„дәӨзәҝгҖӮеҪ“дҪҝз”ЁIntTools_FaceFaceжқҘи®ЎҪҺ—дёӨдёӘйқўзҡ„дәӨҫUҝж—¶еQҢеҸҜд»ҘзңӢеҲоCәӨҫUҝзҡ„иҢғеӣҙдёҚжӯЈјӢ®пјҢжІЎжңүеӨ„зҗҶеӯ”жҙһжғ…еҶөеQҢз”ҡиҮід№ҹжІЎжңүеӨ„зҗҶйқўзҡ„иҫ№з•ҢгҖӮеҰӮдёӢеӣҫжүҖҪCәзәўиүІзҡ„дәӨзәҝдёЮZӢЙз”ЁIntTools_FaceFaceи®Ўз®—еҫ—еҲ°зҡ„пјҡ
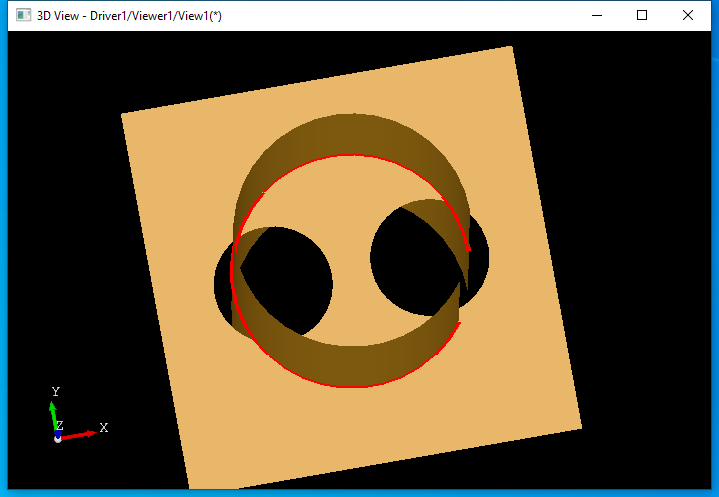
еҪ“дӢЙз”ЁBOPAlgo_PaveFillerи®Ўз®—дәӨзәҝтq¶з»“еҗҲPaveBlockеҫ—еҲ°дәӨзәҝжҳ„ЎӨәеҰӮдёӢеӣҫжүҖҪCәпјҡ
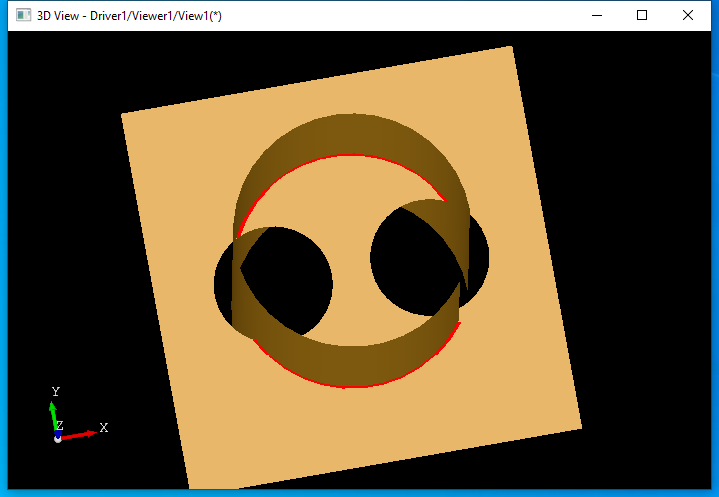
иҷҪ然计算дёӨдёӘйқўд№Ӣй—ҙзҡ„зӣжҖәӨеӨ„зҗҶжңҖҫlҲжҳҜи°ғз”Ёзҡ„IntTools_FaceFaceеQҢдҪҶжҳҜиҰҒеҫ—еҲ°жӯЈзЎ®зҡ„дәӨҫUүKңҖиҰҒдӢЙз”Ёзұ»BOPAlgo_PaveFillerгҖӮиҝҷйҮҢд№ҹз•ҷдёӢй—®йўҳдҫӣеӨ§е®¶жҖқиҖғпјҡдёЮZ»Җд№ҲIntTools_FaceFaceи®Ўз®—зҡ„дәӨҫUҝиҢғеӣҙдёҚжӯЈзЎ®еQҹдШ“д»Җд№ҲBOPAlgo_PaveFillerи®Ўз®—зҡ„дәӨҫUҝжӯЈјӢ®пјҹ
5 Conclusion
ҫlйgёҠжүҖҳqҺНјҢеёғе°”ж•°жҚ®дёӯйқўзҡ„зӣёдәӨзҡ„ҫl“жһңеҸҜиғҪжңүдәӨҫUҝпјҢд№ҹеҸҜиғҪжңүдәӨзӮ№гҖӮе°ҶжұӮдәӨҫl“жһңдҝқеӯҳеҲ°FaceInfoдёӯгҖӮд»ҺҪҺҖеҚ•зҡ„дёӨдёӘтqійқўйҮҚеҸ жқҘзңӢеQҢе°ҶйҮҚеҸ зҡ„зҠ¶жҖҒз”ЁеҸҳйҮҸtheTangetFacesжқҘдҝқеӯҳгҖӮйӮЈд»АL„ҸдёӨдёӘжӣІйқўйҮҚеҸ еҰӮдҪ•еҲӨж–ӯе‘ўпјҹйқўзҡ„зӣжҖәӨиҷҪ然жҸҗдҫӣҫc»IntTools_FaceFaceжқҘи®ЎҪҺ—пјҢдҪҶжҳҜжІЎжңүжӯЈзЎ®еӨ„зҗҶдәӨзәҝзҡ„иҢғеӣЯ_јҢдёЮZ»Җд№ҲBOPAlgo_PaveFillerдёӯеҸҜд»ҘжӯЈјӢ®еӨ„зҗҶдәӨҫUҝе‘ўеQ?/p>
јңқеӨ§е®¶дёӯҝUӢеӣҪеәҶиҠӮж—Ҙеҝ«д№җпјҒ
1 Introduction
еңЁOpenCASCADEдёӯеҜ№дәҺиҫ№зҡ„зӣёдәӨеҲҶдёЮZёүҫc»пјҡиҫ№дёҺзӮ№пјҢиҫ№дёҺиҫ№пјҢиҫ№дёҺйқўпјҢиҫ№дёҺзӮ№зҡ„зӣжҖәӨе·Із»ҸеҪ’з»“дёәзӮ№дёҺиҫ№зҡ„зӣёдәӨеӨ„зҗҶдәҶеQҢиҫ№зҡ„зӣёдәӨдё»иҰҒеӨ„зҗҶиҫ№дёҺиҫ№еQҢиҫ№дёҺйқўзҡ„зӣёдәӨгҖӮиҫ№дёҺиҫ№гҖҒиҫ№дёҺйқўзҡ„зӣёдәӨдјҡеј•е…ҘдёҖдёӘж–°зҡ„ж•°жҚ®з»“жһ?е…¬е…ұйғЁеҲҶCommon PartеQҢз”ЁдәҺдҝқеӯҳйҮҚеҸ зҡ„е…¬е…ұйғЁеҲҶж•°жҚ®гҖ?/p>
2 Edge/Edge Interferences
еҜ№дәҺдёӨжқЎиҫ№зҡ„зӣжҖәӨжҳҜжҢҮеңЁдёӨжқЎиҫ№зҡ„жҹҗдәӣең°ж–№зҡ„и·қзҰ»һ®ҸдәҺиҫ№зҡ„е®№е·®д№Ӣе’ҢеQҢдё»иҰҒеҲҶдёЮZёӨҝUҚжғ…еҶөпјҢдёҖҝUҚжҳҜдёӨжқЎиҫ№еҸӘжңүдёҖдёӘдәӨзӮ№зҡ„жғ…еҶөеQӣдёҖҝUҚжҳҜжңүйҮҚеҸ йғЁеҲҶзҡ„жғ…еҶөеQӣе…ҲзңӢеҸӘжңүдёҖдёӘдәӨзӮТҺғ…еҶөпјҡ

жҲ‘们еңЁDRAWдёӯйҖҡиҝҮи„ҡжң¬жһ„йҖ жңҖҪҺҖеҚ•зҡ„жғ…еҶөжқҘжөӢиҜ•гҖ?/p>
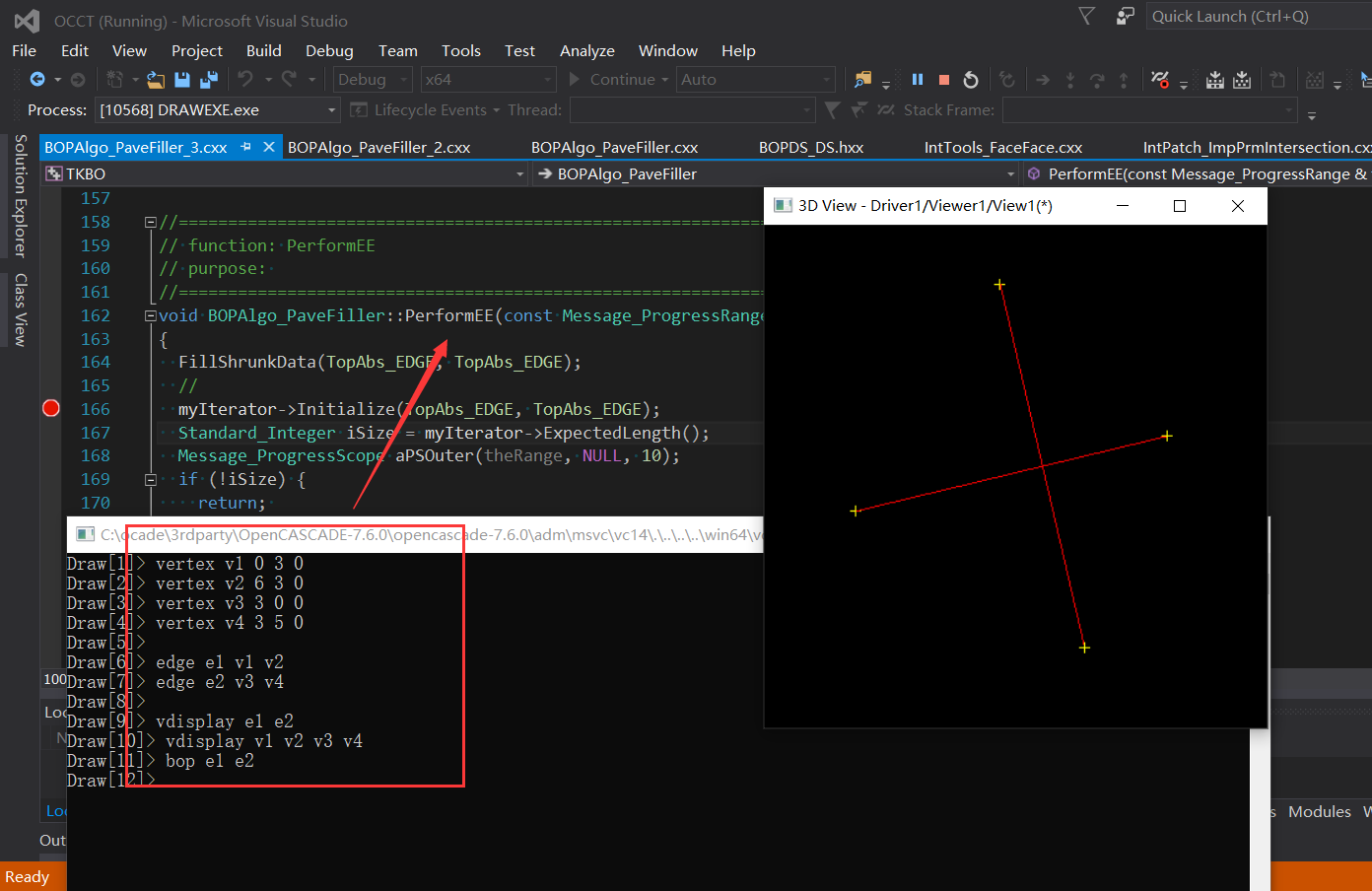
еңЁеӨ„зҗҶиҫ№дёҺиҫ№зӣжҖәӨзҡ„еҮҪж•°BOPAlgo_PaveFiller::PerformEE()дёӯпјҢеҜТҺҜҸдёӨжқЎиҫ№и°ғз”ЁBOPAlgo_EdgeEdgeҳqӣиЎҢжұӮдәӨгҖӮд»ҺҳqҷйҮҢеҸҜд»ҘзңӢеҲ°Pave Blockзҡ„дӢЙз”ЁпјҢзӣёеҪ“дәҺеҜ№жҜҸдёӨжқЎиҫ№дёҠзҡ„жҜҸеҜ№Pave BlockйғЁеҲҶҳqӣиЎҢжұӮдәӨгҖӮиҝҷйҮҢжңүдёҖдәӣдјҳеҢ–з©әй—Я_јҢзӣ®еүҚжҳҜдӢЙз”Ёзҡ„дёӨдёӘеҫӘзҺҜеӨ„зҗҶеQҢеҸҜд»Ҙе°қиҜ•дӢЙз”ЁBVHжқҘжҸҗеҚҮдёҖдәӣжҖ§иғҪгҖӮеҪ“жҜҸеҜ№Pave BlockеҜ№еә”зҡ„зӮ№зҡ„зғҰеј•еҸ·дёҖиҮҙж—¶еQҢеҚіжҜҸеҜ№Pave Blockзҡ„з«ҜзӮҡwҮҚеҸ ж—¶еQҢдӢЙз”Ёеҝ«йҖҹи®ЎҪҺ—зҡ„ҪҺ—жі•жқҘеҲӨж–ӯжҳҜеҗҰжңүйҮҚеҸ гҖ?/p>
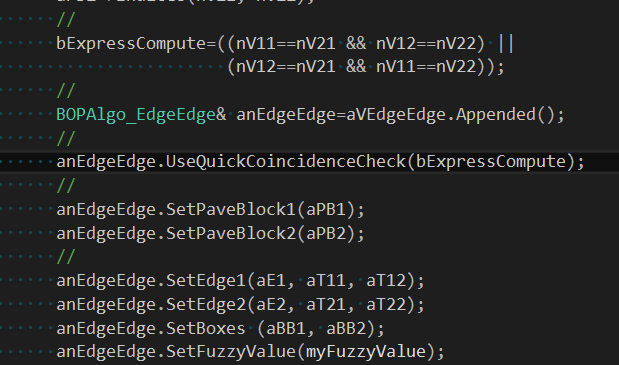
еҜ№дәҺиҫ№зҡ„жұӮдәӨҫl“жһңдҝқеӯҳеҲ°BOPDS_InterfEEдёӯпјҢйғҪдјҡдҝқеӯҳжҳҜе“ӘдёӨжқЎиҫ№зӣёдәӨеҸҠзӣжҖәӨзҡ„е…¬е…ұйғЁеҲҶгҖӮеҜ№дәҺзӣёдәӨдәҺдёҖзӮ№зҡ„е…¬е…ұйғЁеҲҶзҡ„зұ»еһӢдШ“TopAbs_VERTEXеQҢеҜ№дәҺжңүйҮҚеҸ йғЁеҲҶзҡ„е…¬е…ұйғЁеҲҶзұ»еһӢдШ“TopAbs_EDGEеQ?/p>

еҪ“дёӨиҫТҺқЎжңүйҮҚеҸ йғЁеҲҶж—¶еQҢеҰӮдёӢеӣҫжүҖҪCәпјҡ
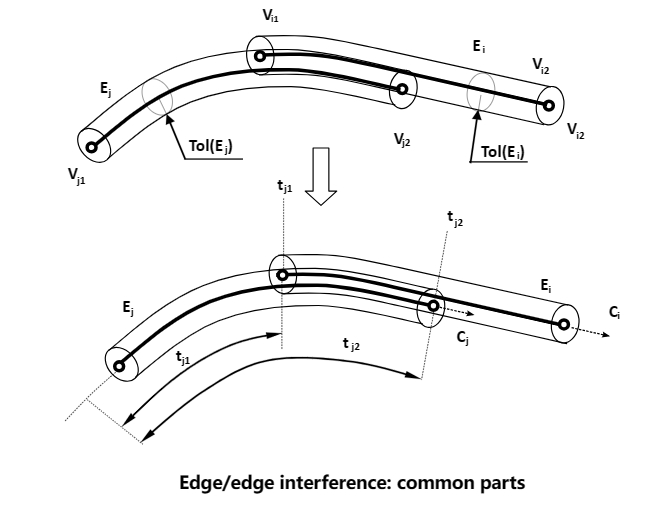
еҰӮдҪ•ӢӮҖӢ№ӢдёӨжқЎиҫ№зҡ„е…¬е…ұйғЁеҲҶе‘ўеQҹеңЁеҮҪж•°IntTools_EdgeEdge::IsCoincident()дёӯе®һзҺҺНјҡ
//=======================================================================
//function : IsCoincident
//purpose :
//=======================================================================
Standard_Boolean IntTools_EdgeEdge::IsCoincident()
{
Standard_Integer i, iCnt, aNbSeg, aNbP2;
Standard_Real dT, aT1, aCoeff, aTresh, aD;
Standard_Real aT11, aT12, aT21, aT22;
GeomAPI_ProjectPointOnCurve aProjPC;
gp_Pnt aP1;
//
aTresh=0.5;
aNbSeg=23;
myRange1.Range(aT11, aT12);
myRange2.Range(aT21, aT22);
//
aProjPC.Init(myGeom2, aT21, aT22);
//
dT=(aT12-aT11)/aNbSeg;
//
iCnt=0;
for(i=0; i <= aNbSeg; ++i) {
aT1 = aT11+i*dT;
myGeom1->D0(aT1, aP1);
//
aProjPC.Perform(aP1);
aNbP2=aProjPC.NbPoints();
if (!aNbP2) {
continue;
}
//
aD=aProjPC.LowerDistance();
if(aD < myTol) {
++iCnt;
}
}
//
aCoeff=(Standard_Real)iCnt/((Standard_Real)aNbSeg+1);
return aCoeff > aTresh;
}д»ҺдёҠҳqоC»Јз ҒеҸҜд»ҘзңӢеҮәпјҢеҜ№дәҺйҮҚеҸ йғЁеҲҶзҡ„жЈҖӢ№ӢжҳҜһ®ҶдёҖжқЎиҫ№ж ТҺҚ®ӢӮҖӢ№ӢиҢғеӣҙеҲҶжҲ?3ҢDөйҮҮж пLӮ№еQҢи®ЎҪҺ—жҜҸдёӘзӮ№еҲ°еҸҰдёҖжқЎиҫ№зҡ„и·қјӣ»пјҢж»ЎиғцжқЎдҡgзҡ„йҮҮж пLӮ№зҡ„ж•°йҮҸи¶…ҳq?2дёӘпјҢеҹәжң¬и®ӨдШ“жҳҜйҮҚеҸ зҡ„гҖӮд»ҺҳqҷйҮҢеҸҜд»ҘзңӢеҮәҳqҷж ·ӢӮҖӢ№ӢйҮҚеҸ зЁҚеҫ®жңүзӮ№дёҚдёҘи°}гҖӮеӣәе®ҡйҮҮж пLӮ№ж•°йҮҸеҜ№дәҺһ®Ҹж®өжӣІзәҝжқҘиҜҙж•°йҮҸҳqҮеӨ§еQҢеҜ№дәҺеҫҲй•ҝзҡ„жӣІзәҝжқҘиҜҙж•°йҮҸеҸҲеҒҸһ®ҸпјҢҳqҷйҮҢжңүеҫ…жҸҗй«ҳгҖӮеҰӮжһңйҮҚеҸ пјҢеҲҷе°Ҷе…¬е…ұйғЁеҲҶзҡ„ж•°жҚ®дҝқеӯҳи“vжқҘпјҡ

еҜ№дәҺӢ№ӢиҜ•зҡ„TCLи„ҡжң¬дёҚдјҡиө°иҝҷдёӘйҖҡз”Ёзҡ„еҲӨж–ӯжөҒҪEӢпјҢдјҡзӣҙжҺҘжңүIntTools_EdgeEdge::ComputeLineLine()еҮҪж•°жқҘеӨ„зҗҶиҝҷҝUҚзү№ҢDҠжғ…еҶөпјҡ
д»Һдҝқеӯҳзҡ„ж•°жҚ®еҸҜд»ҘзңӢеҮәеQҢе…¬е…ұйғЁеҲҶзҡ„зӣжҖәӨҫcХdһӢдёәTopAbs_VERTEXеQҢеҸҠдәӨзӮ№еҲҶеҲ«еңЁдёӨжқЎиҫ№дёҠзҡ„еҸӮж•°гҖӮе…ідәҺжңүйҮҚеҸ йғЁеҲҶзҡ„дёӨжқЎиҫ№зӣжҖәӨеQҢеҗҢеӯҰ们еҸҜд»ҘиҮӘиЎҢдҪҝз”ЁDRAWи„ҡжң¬жқҘжөӢиҜ•дёҖдёӢгҖ?/p>
3 Edge/Face Interferences
иҫ№дёҺйқўзҡ„зӣжҖәӨдјҡйҒҮеҲ°е’Ңиҫ№дёҺиҫ№зӣёдәӨзұ»дјјзҡ„жғ…еҶөеQҢеҚідјҡжңүйҮҚеҸ йғЁеҲҶCommon PartгҖӮд№ҹеҲҶдШ“дёӨз§Қжғ…еҶөеQҢдёҖҝUҚжғ…еҶү|ҳҜиҫ№дёҺйқўеҸӘжңүдёҖдёӘдәӨзӮ№зҡ„жғ…еҶөеQҢдәӨзӮ№еҸҜиғҪдјҡжңүеӨҡдёӘпјӣдёҖҝUҚжғ…еҶү|ҳҜжңүйҮҚеҸ йғЁеҲҶзҡ„жғ…еҶөгҖ?/p>
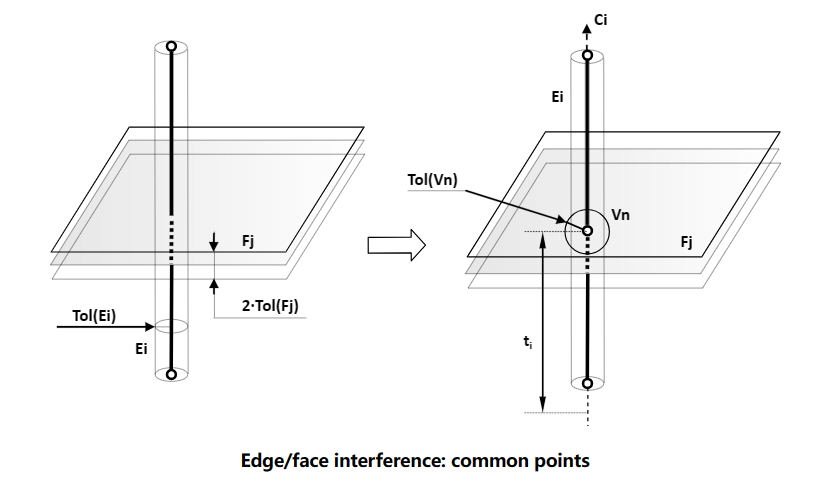
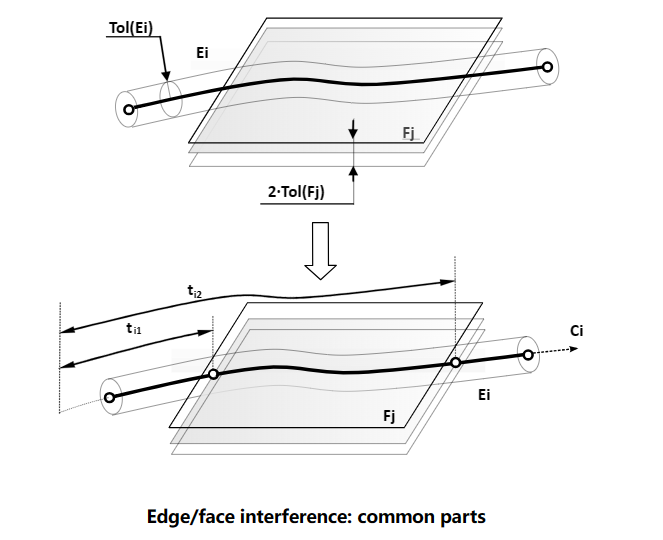
жҲ‘们еҸҜд»ҘеңЁдӢЙз”Ёи„ҡжң¬жқҘӢ№ӢиҜ•дёҖдёӢйҮҚеҸ зҡ„жғ…еҶөеQ?/p>
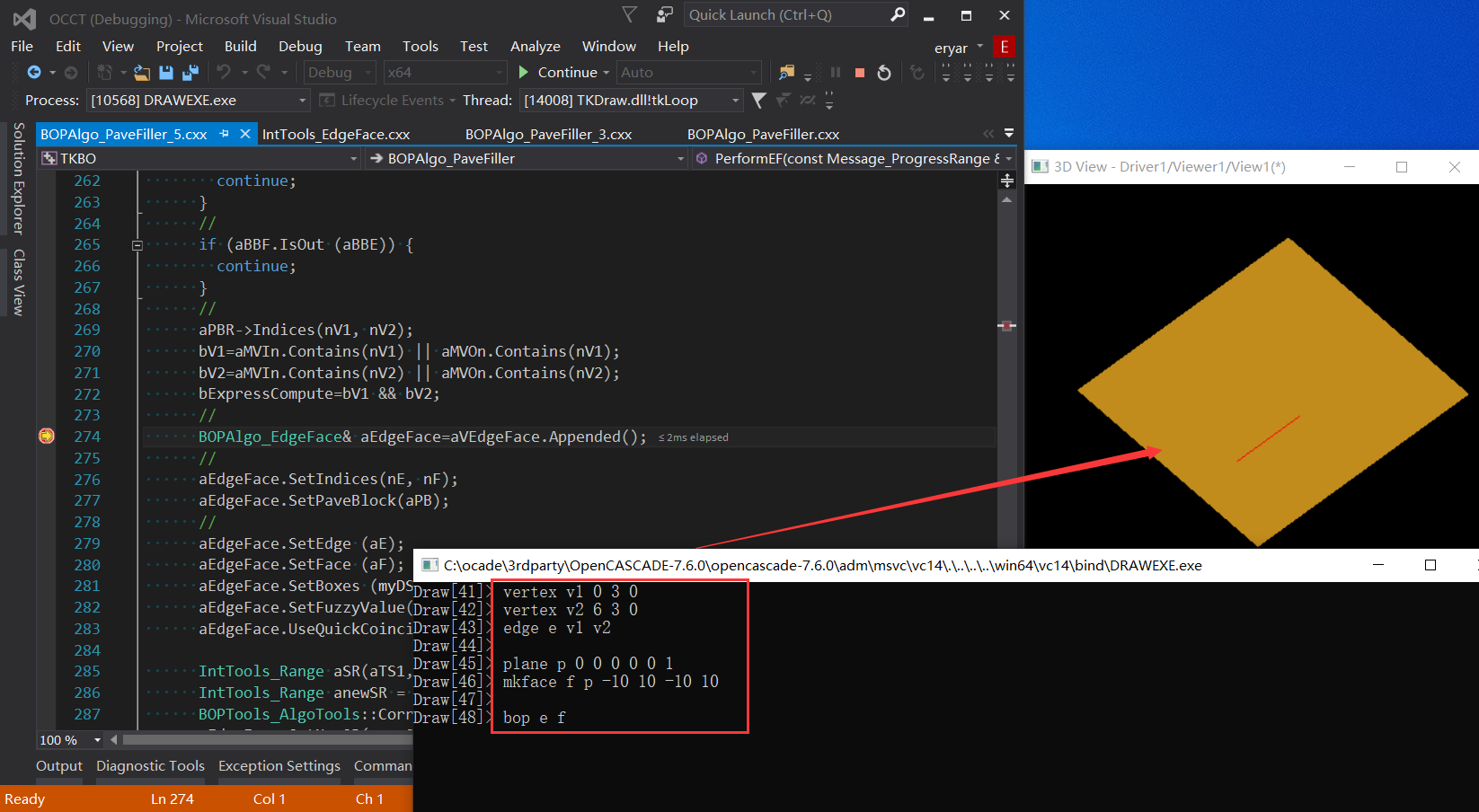
д»Һд»Јз ҒдёӯеҸҜд»ҘзңӢеҮәеҪ“иҫ№зҡ„з«ҜзӮ№еңЁйқўдёҠж—УһјҢеҲҷдјҡеҲӨж–ӯиҫ№дёҺйқўдјҡдёҚдјҡйҮҚеҸ CoincidenceгҖӮеҲӨж–ӯйҖ»иҫ‘дёҺеҲӨж–ӯиҫ№жҳҜеҗҰйҮҚеҸ ҫcЦMјјеQҢйғҪжҳҜдӢЙз”Ёеӣәе®?3дёӘйҮҮж пLӮ№зҡ„ж–№ејҸеӨ„зҗҶпјҢтq¶еҠ дёҠе®ҡдҪҚеҷЁжқҘеҲӨж–ӯзӮ№жҳҜеҗҰеңЁйқўдёҠпјҢеӣ дШ“йқўдёҠеҸҜиғҪдјҡжңүеӯ”жҙһеQ?/p>
//=======================================================================
//function : IsCoincident
//purpose :
//=======================================================================
Standard_Boolean IntTools_EdgeFace::IsCoincident()
{
Standard_Integer i, iCnt;
Standard_Real dT, aT, aD, aT1, aT2, aU, aV;
gp_Pnt aP;
TopAbs_State aState;
gp_Pnt2d aP2d;
//
GeomAPI_ProjectPointOnSurf& aProjector=myContext->ProjPS(myFace);
Standard_Integer aNbSeg=23;
if (myC.GetType() == GeomAbs_Line &&
myS.GetType() == GeomAbs_Plane)
aNbSeg = 2; // Check only three points for Line/Plane intersection
const Standard_Real aTresh = 0.5;
const Standard_Integer aTreshIdxF = RealToInt((aNbSeg+1)*0.25),
aTreshIdxL = RealToInt((aNbSeg+1)*0.75);
const Handle(Geom_Surface) aSurf = BRep_Tool::Surface(myFace);
aT1=myRange.First();
aT2=myRange.Last();
Standard_Real aBndShift = 0.01 * (aT2 - aT1);
//Shifting first and last curve points in order to avoid projection
//on surface boundary and rejection projection point with minimal distance
aT1 += aBndShift;
aT2 -= aBndShift;
dT=(aT2-aT1)/aNbSeg;
//
Standard_Boolean isClassified = Standard_False;
iCnt=0;
for(i=0; i <= aNbSeg; ++i) {
aT = aT1+i*dT;
aP=myC.Value(aT);
//
aProjector.Perform(aP);
if (!aProjector.IsDone()) {
continue;
}
//
aD=aProjector.LowerDistance();
if (aD > myCriteria) {
if (aD > 100. * myCriteria)
return Standard_False;
else
continue;
}
//
++iCnt;
//We classify only three points: in the begin, in the
//end and in the middle of the edge.
//However, exact middle point (when i == (aNbSeg + 1)/2)
//can be unprojectable. Therefore, it will not be able to
//be classified. Therefore, points with indexes in
//[aTreshIdxF, aTreshIdxL] range are made available
//for classification.
//isClassified == TRUE if MIDDLE point has been chosen and
//classified correctly.
if(((0 < i) && (i < aTreshIdxF)) || ((aTreshIdxL < i ) && (i < aNbSeg)))
continue;
if(isClassified && (i != aNbSeg))
continue;
aProjector.LowerDistanceParameters(aU, aV);
aP2d.SetX(aU);
aP2d.SetY(aV);
IntTools_FClass2d& aClass2d=myContext->FClass2d(myFace);
aState = aClass2d.Perform(aP2d);
if(aState == TopAbs_OUT)
return Standard_False;
if(i != 0)
isClassified = Standard_True;
}
//
const Standard_Real aCoeff=(Standard_Real)iCnt/((Standard_Real)aNbSeg+1);
return (aCoeff > aTresh);
}жұӮдәӨҫl“жһңдёҺиҫ№дёҺиҫ№зӣжҖәӨҫcХdһӢеQҢдјҡдҝқеӯҳиҫ№дёҺйқўзҡ„зҙўеј•еQҢеҸҠе…¬е…ұйғЁеҲҶзҡ„ж•°жҚ®гҖӮйҷӨдәҶдҝқеӯҳиҝҷдәӣж•°жҚ®д»ҘеӨ–пјҢҳqҳе’ҢзӮ№дёҺйқўзӣёдәӨдёҖж шPјҢжӣҙж–°йқўдёҠзҡ„дҝЎжҒҜFaceInfoеQҢеҚіжңүе“Әдәӣиҫ№еңЁйқўдёҠгҖ?/p>
4 Conclusion
ҫlйgёҠжүҖҳqҺНјҢиҫ№дёҺиҫҸVҖҒиҫ№дёҺйқўзӣжҖәӨдјҡеҫ—еҲ°е…¬е…ұйғЁеҲҶCommon PartеQҢе…¬е…ұйғЁеҲҶеҸҜиғҪжҳҜзӮ№пјҢд№ҹеҸҜиғҪжҳҜйҮҚеҸ зҡ„иҫ№гҖӮеңЁҳqҮжЧoзӣжҖәӨзҡ„иҫ№дёҺиҫ№гҖҒиҫ№дёҺйқўж—үҷғҪжңүдёҖе®ҡзҡ„дјҳеҢ–ҪIәй—ҙеQҢеҚідҪҝз”ЁBVHжқҘеҠ йҖҹжЈҖӢ№ӢзӣёдәӨйғЁеҲҶгҖӮеңЁеҝ«йҖҹеҲӨж–ӯиҫ№дёҺиҫ№жҳҜеҗҰйҮҚеҸ гҖҒиҫ№дёҺйқўжҳҜеҗҰйҮҚеҸ йғЁеҲҶзҡ„д»Јз ҒйҮҮз”Ёеӣәе®ҡж•°йҮҸзҡ„йҮҮж ·зӮ№зҡ„еӨ„зҗҶж–№ејҸдёҚеӨӘдёҘи°}гҖӮе°ҶзӣжҖәӨзҡ„з»“жһңеҸҠҳqҮзЁӢж•°жҚ®йғҪдҝқеӯҳеҲ°BOPDS_DSдёӯдҪңдёәеҗҺйқўз®—жі•дӢЙз”ЁгҖ?/p>
1 IMGUI
ImGui жҳҜдёҖдёӘз”ЁдәҺC++зҡ„з”ЁжҲпL•Ңйқўеә“еQҢи·Ётqӣ_Ҹ°гҖҒж— дҫқиө–еQҢж”ҜжҢҒOpenGLгҖҒDirectXҪ{үеӨҡҝUҚжёІжҹ“APIеQҢжҳҜдёҖҝUҚеҚіж—¶UIеQҲImmediate Mode User InterfaceеQүеә“еQҢдҝқз•ҷжЁЎејҸдёҺеҚПx—¶жЁЎејҸзҡ„еҢәеҲ«еҸӮиҖ?a target="_blank" rel="noopener">дҝқз•ҷжЁЎејҸдёҺеҚіж—¶жЁЎеј?/strong>гҖӮImGuiжёІжҹ“йқһеёёеҝ«пјҢдҪҶз•ҢйқўдёҠжңүеӨ§йҮҸзҡ„ж•°жҚ®йӣҶйңҖиҰҒжёІжҹ“еҸҜиғҪдјҡжңүдёҖдәӣй—®йўҳпјҢйңҖиҰҒдӢЙз”ЁдёҖдәӣзј“еӯҳжҠҖе·§гҖӮзј“еӯҳеҸӘжҳҜйҒҝе…Қж•°жҚ®зҡ„жӣҙж–°йҖ»иҫ‘иҖ—ж—¶еӨӘд№…еҪұе“ҚжёІжҹ“еQҢе®һйҷ…жёІжҹ“иҝҮҪEӢдёҚеӯҳеңЁз“үҷўҲгҖ?/p>
IMGUIеҫҲиҪ»йҮҸпјҢҳqҳж”ҜжҢҒи·Ётqӣ_Ҹ°еQҢеҜ№дәҺе°Ҹзҡ„жөӢиҜ•зЁӢеәҸIMGUIжҳҜзҗҶжғізҡ„GUIгҖ?/p>
еҹЮZәҺopencascadeзҡ„glfw sampleеҠ е…ҘIMGUIеQҢиҝҷж ·е°ұеҸҜд»ҘејҖеҸ‘дёҖдәӣеёҰжңүGUIзҡ„зЁӢеәҸгҖӮиҝҷдәӣзЁӢеәҸе°Ҹе·§дё”иғҪж–№дҫҝи·Ётqӣ_Ҹ°еQҢзңӢдёҠеҺ»ж•Ҳжһңд№ҹдёҚй”ҷгҖ?/p>
зҺ°еңЁһ®ҶOcctImguiејҖжәҗпјҢејҖжәҗең°еқҖеQҡhttps://github.com/eryar/OcctImgui дҪҝз”ЁPremakeжқҘз”ҹжҲҗи§ЈеҶПx–№жЎҲпјҢеҸӘйңҖиҰҒе°Ҷpremake5.luaдёӯзҡ„зӣёе…іҪW¬дёүж–№еә“зҡ„иө\еҫ„дҝ®ж”№дёҖдёӢпјҢеҚӣ_ҸҜд»ҘзӣҙжҺҘзј–иҜ‘иҝҗиЎҢгҖ?/p>
зӣ®еүҚocctзҡ„и§ҶеӣҫдҪңдёәж•ҙдёӘиғҢжҷҜпјҢдёӢдёҖжӯҘеҸҜд»ҘеҒҡжҲҗеғҸCADRaysдёӯйӮЈж шPјҢһ®Ҷocctзҡ„и§ҶеӣҫдҪңдёшҷ§Ҷеӣ„Ўҡ„дёҖйғЁеҲҶеQҢиҝҷж ·е°ұеҸҜд»ҘдҪҝз”ЁIMGUIзҡ„DockingеҠҹиғҪгҖ?/p>
дҪҝз”ЁIMGUIд№ҹеҸҜд»ҘејҖеҸ‘еҮәеҫҲCoolзҡ„з•ҢйқўпјҢжңҖеҗҺж”ҫдёӨдёӘеҹЮZәҺIMGUIејҖеҸ‘зҡ„еӣ‘ЦЕһз•ҢйқўеQ?/p>
https://github.com/adriengivry/Overload https://github.com/sasobadovinac/CADRays https://github.com/MeshInspector/MeshLib2 OcctImgui
3 Next