性能提升-空間二叉查找樹
Abstract. OpenCASCADE provides NCollection_UBTree to achieve high performance search overlapped boxes. The algorithm of unbalanced binary tree of overlapped bounding boxes. Once the tree of boxes of geometric objects is constructed, the algorithm is capable of fast geometric selection of objects. The tree can be easily updated by adding to it a new object with bounding box. The time of adding to the tree of one object is O(log(N)), where N is the total number of objects, so the time of building a tree of N objects is O(N(log(N)). The search time of one object is O(log(N)). Defining various classes inheriting NCollection_UBTree::Selector we can perform various kinds of selection over the same b-tree object.
Key Words. Unbalanced Binary Tree, Binary Search Tree, Binary Sort Tree, Bounding Box
1 Introduction
非平衡二叉樹(Unbalanced Binary Tree)又叫二叉查找樹(Binary Search Tree)或二叉排序樹(Binary Sort Tree)。它的定義很簡單,就是左子樹上所有節(jié)點(diǎn)的值都要小于根節(jié)點(diǎn)上的值。右子樹上所有節(jié)點(diǎn)值都要大于根節(jié)點(diǎn)上的值。在二叉查找樹上執(zhí)行操作時間與樹的高度成正比。對于一棵含有n個結(jié)點(diǎn)的完全二叉樹,這些操作的最壞情況運(yùn)行時間為O(lg(n))。但是如果樹是含n個結(jié)點(diǎn)的線性鏈,則這些操作的最壞的情況運(yùn)行時間為O(n)。一棵隨機(jī)構(gòu)造的二叉查找樹的期望高度為O(lg(n)),從而這種樹上操作的平均時間為O(lg(n))。
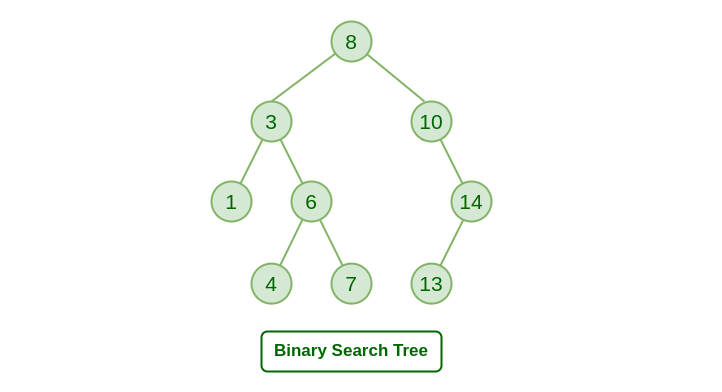
幾何搜索(geometry searching)大致分兩類:一類是區(qū)域搜索問題(range searching problem),另一類是點(diǎn)的定位問題(point location problem)。區(qū)域搜索問題要回答的是給定一個區(qū)域,看有多少模型屬于這個區(qū)域。當(dāng)然,我們可以對所有模型進(jìn)行遍歷,這種算法時間復(fù)雜度為O(N),效率不高。常見的高效的區(qū)域搜索算法有k-D樹,k-D樹就是一種多維的平衡二叉樹。還有比較常見的KNN問題,這些都是計算幾何處理的問題。
OpenCASCADE中提供一種空間查找二叉樹算法NCollection_UBTree,字面意思是非平衡二叉樹Unbalanced Binary Tree。把上圖中的數(shù)字換成包圍盒,構(gòu)造二叉查找樹。為了解決查找二叉樹單鏈問題,加入隨機(jī)處理,可以使查找性能達(dá)到O(log(N)),相對普通遍歷速度而言還是不錯的。本文結(jié)合示例代碼說明如何使用這個非平衡二叉樹。
2 Example
在OpenCASCADE中有多個函數(shù)來實(shí)現(xiàn)將很多無序邊Edges連接成Wire,需要查詢一條邊Edge的一個頂點(diǎn)Vertex在一定精度范圍內(nèi)相連的頂點(diǎn)Vertex有哪些?
首先,實(shí)現(xiàn)一個選擇類,通過選擇類來進(jìn)行過濾:
typedef NCollection_UBTree<Standard_Integer, Bnd_Box> BoxTree;
typedef NCollection_UBTreeFiller<Standard_Integer, Bnd_Box> BoxTreeFiller;
class BoxSelector : public BoxTree::Selector
{
public:
BoxSelector(const TColgp_SequenceOfPnt& thePoints, Standard_Real theTolerance)
: Selector()
, myPoints(thePoints)
, myTolerance(theTolerance)
{
}
virtual Standard_Boolean Reject(const Bnd_Box& theBox) const
{
return theBox.IsOut(myBox);
}
virtual Standard_Boolean Accept(const Standard_Integer& theIndex)
{
if (theIndex > myPoints.Size() || theIndex == myIndex)
{
return Standard_False;
}
const gp_Pnt& aPnt = myPoints.Value(theIndex);
if (aPnt.SquareDistance(myPnt) < myTolerance)
{
myResultIndex.Append(theIndex);
return Standard_True;
}
return Standard_False;
}
void SetCurrentPoint(const gp_Pnt& thePnt, Standard_Integer theIndex)
{
myPnt = thePnt;
myBox.Add(thePnt);
myIndex = theIndex;
}
const TColStd_ListOfInteger& GetResultIndex() const
{
return myResultIndex;
}
void ClearResultIndex()
{
myResultIndex.Clear();
}
protected:
private:
const TColgp_SequenceOfPnt& myPoints;
gp_Pnt myPnt;
Bnd_Box myBox;
Standard_Integer myIndex;
Standard_Real myTolerance;
TColStd_ListOfInteger myResultIndex;
};主要實(shí)現(xiàn)兩個抽象函數(shù)Reject()和Accept(),以及設(shè)置當(dāng)前選擇器的狀態(tài)。Reject()函數(shù)用來判斷要查找的Box與當(dāng)前空間范圍的狀態(tài),如果在外,則返回True。當(dāng)兩個Box有相交時,會調(diào)用Accept()函數(shù),在此函數(shù)中判斷兩個點(diǎn)的距離是否在容差范圍內(nèi),若在容差范圍內(nèi),則將點(diǎn)記錄起來。主函數(shù)main代碼如下:
int main(int argc, char* argv[])
{
// Fill tree with random points.
BoxTree aBoxTree;
BoxTreeFiller aTreeFiler(aBoxTree);
math_BullardGenerator aRandom;
TColgp_SequenceOfPnt aPoints;
for (Standard_Integer i = 1; i <= 100; ++i)
{
gp_Pnt aPnt(aRandom.NextReal(), aRandom.NextReal(), aRandom.NextReal());
aPoints.Append(aPnt);
Bnd_Box aBox;
aBox.Add(aPnt);
aTreeFiler.Add(i, aBox);
}
aTreeFiler.Fill();
// Query points near the given point.
BoxSelector aSelector(aPoints, 0.1);
for (Standard_Integer i = aPoints.Lower(); i <= aPoints.Upper(); ++i)
{
const gp_Pnt& aPnt = aPoints.Value(i);
aSelector.SetCurrentPoint(aPnt, i);
Standard_Integer aSize = aBoxTree.Select(aSelector);
if (aSize > 0)
{
std::cout << "Search Point : " << aPnt.X() << " \t " << aPnt.Y() << " \t " << aPnt.Z() << std::endl;
const TColStd_ListOfInteger& aResult = aSelector.GetResultIndex();
for (TColStd_ListOfInteger::Iterator aIt(aResult); aIt.More(); aIt.Next())
{
const gp_Pnt& aPoint = aPoints.Value(aIt.Value());
std::cout << "Target Point : " << aPoint.X() << " \t " << aPoint.Y() << " \t " << aPoint.Z() << std::endl;
}
std::cout << "=============================" << std::endl;
}
aSelector.ClearResultIndex();
}
return 0;
}先用隨機(jī)函數(shù)隨機(jī)生成100個點(diǎn),并將點(diǎn)通過BoxTreeFiller添加到查找樹aBoxTree中,調(diào)用Fill函數(shù)構(gòu)造查找樹。
再使用類BoxSelector來進(jìn)行快速查找,查找之前先設(shè)置當(dāng)前點(diǎn)及包圍盒。然后調(diào)用aBoxTree.Select(aSelector)進(jìn)行查找。
3 Conclusion
類NCollection_UBTree通過構(gòu)造包圍盒的非平衡二叉樹來加快區(qū)域搜索速度。如何提高搜索速度,是計算幾何處理的范疇。在OpenCASCADE中這個類使用場景比較多,如將無序邊構(gòu)造成Wire時都用這個類:BRepLib_MakeWire::Add(const TopTools_ListOfShape& L), ShapeAnalysis_FreeBounds::ConnectEdgesToWires()。包括后面引入的BVH都是為了提高搜索速度,在合適的場景中多使用這些算法,會對程序性能的提升有很大幫助。





