OpenCASCADE曲面求交之網格離散法1

eryar@163.com

1 Introduction

由朱心雄等著《自由曲線曲面造型技術》書中對曲面求交之網格離散法描述如下：該法的基本思想是先將曲面離散為由小平面片組成的網格，當網格足夠密時，可以認為已經非常接近真實曲面，對分別表示不同曲面的兩張網格，利用平面片求交法求得的交線，并以此交線近似代表曲面間的交線。這種方法原理簡明，便于實現，適用范圍廣，任意參數曲面均可利用該法求交。但為獲取精確地交線，則必須生成非常細密的網格，這將導致占用內存多，計算花費大。因此，實際工作中很少單一使用離散網格法，而常將其與其他方法結合使用。

OpenCASCADE中對于曲面求交也提供離散網格法，其中曲面的離散網格由類IntPatch_Polyhedron表示，兩個網格面求交使用類IntPatch_InterferencePolyhedron。本文主要介紹曲面的網格表示類IntPatch_Polyhedron。

2 Polyhedron

OpenCASCADE用于曲面求交的網格離散算法相對BRepMesh中的算法要簡單很多，主要思路是根據參數U，V方向上的采樣點數量來計算曲面上的點，再根據固定公式將采樣點連成三角形。其中生成采樣點代碼如下所示：

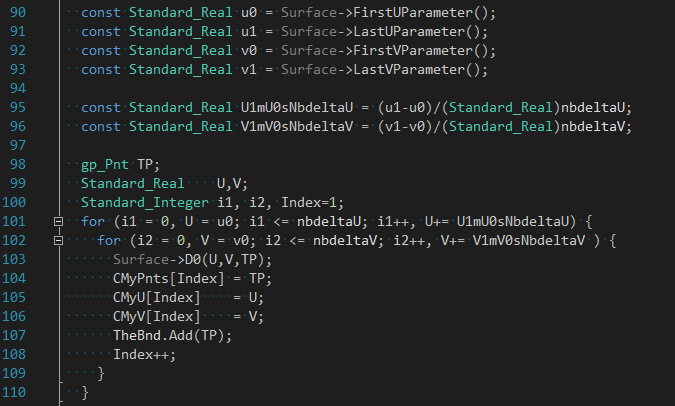
成員變量CMyPnts是采樣點數組，CMyU和CMyV是采樣點在曲面上的參數。將采樣點連成三角形函數如下圖所示：

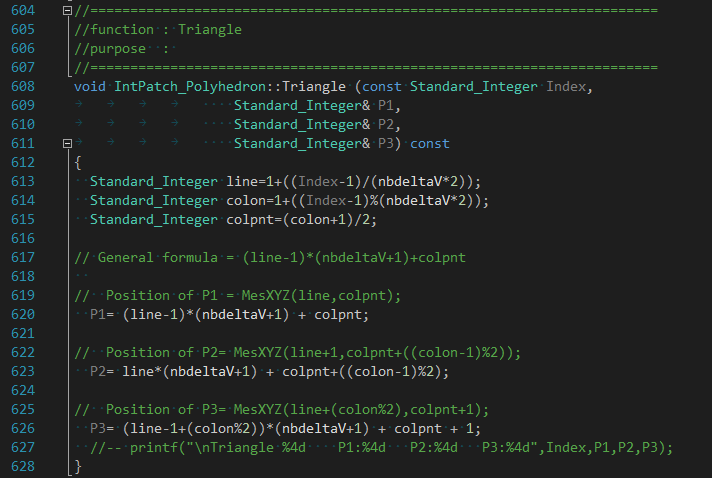
根據上述生成采樣點及三角形函數，對于平面生成的三角形如下圖所示：

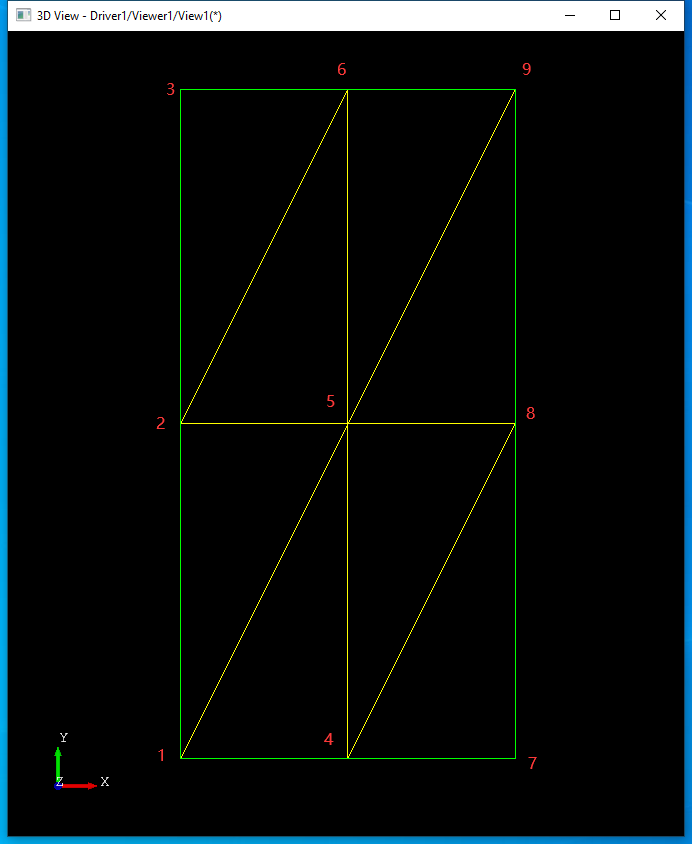
其中Triangle()函數中變量line表示參數u方向上第幾條線，代入具體的索引Index來看規律：

當參數索引 Index為1時，line為1，得到的三角形為1-4-5；

當參數索引Index為2時，line為1，得到的三角形為1-5-2；

當參數索引Index為3時，line為1，得到的三角形為2-5-6；

當參數索引Index為4時，line為1，得到的三角形為2-6-3；

當參數索引Index為5時，line為2，得到的三角形為4-7-8；

當參數索引Index為6時，line為2，得到的三角形為4-8-5；

從上可以得到生成三角形的規律，即根據索引Index計算正在處理的三角形是參數u方向上第幾條線line，生成這條線上在參數v方向上的所有的三角形。生成的三角形都是逆時針的。

下面我們看看對于一些基本曲面，這種離散網格算法生成的網格效果：

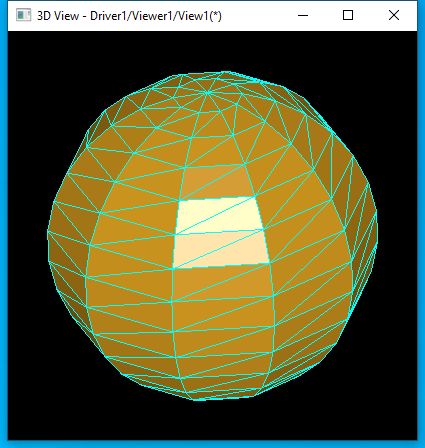
球面的離散網格

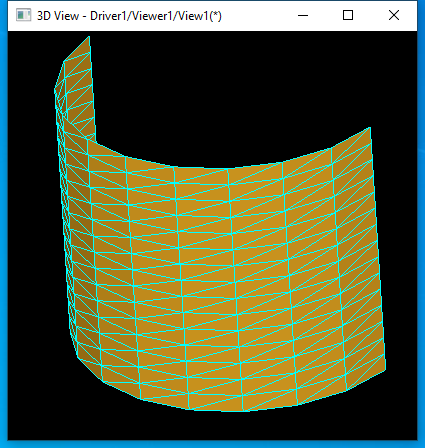
圓柱面的離散網格

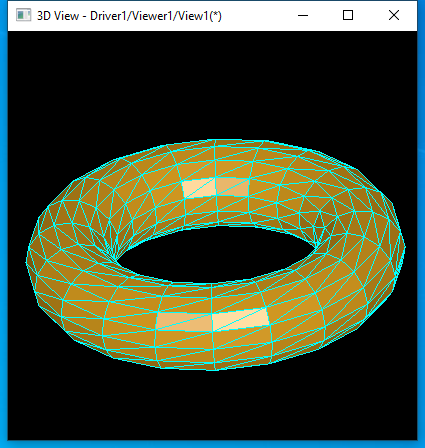
圓環面的離散網格

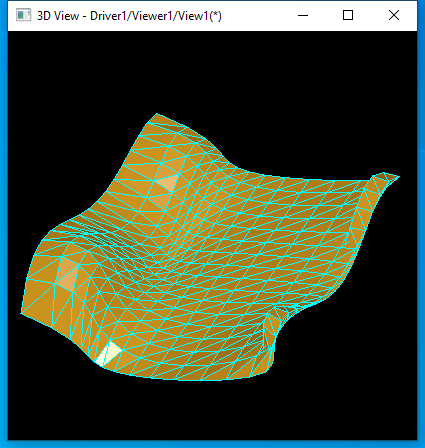
B樣條曲面

3 Conclusion

綜上所述，類IntPatch_Polyhedron中生成網格的算法主要依賴曲面在參數U，V上的采樣點數量。默認采樣點數量是根據函數NbSamplesV()和NbSamplesU()生成。

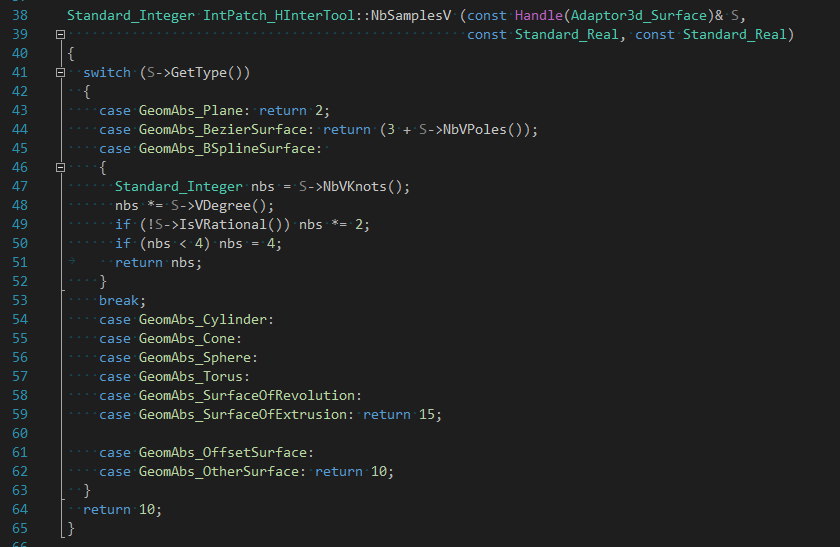
也可以指定采樣點數量，當采樣點數量越多，則生成的三角形越多，網格越密。當然這種方式也可用來生成曲面的顯示數據，生成速度很快，唯一的缺陷是生成顯示用網格的精度只能通過采樣點數量來控制，對于曲率變化大的曲面，若指定多的采樣點，則會生成大量三角形，占用大量內存空間。

附上測試代碼：

#include <TColgp_Array2OfPnt.hxx>
#include <Geom_Plane.hxx>
#include <Geom_CylindricalSurface.hxx>
#include <Geom_ConicalSurface.hxx>
#include <Geom_SphericalSurface.hxx>
#include <Geom_ToroidalSurface.hxx>
#include <Geom_BSplineSurface.hxx>
#include <GeomAdaptor_Surface.hxx>
#include <GeomAPI_PointsToBSplineSurface.hxx>
#include <IntPatch_Polyhedron.hxx>
#include <IntPatch_InterferencePolyhedron.hxx>
#pragma comment(lib, "TKernel.lib")
#pragma comment(lib, "TKMath.lib")
#pragma comment(lib, "TKG2d.lib")
#pragma comment(lib, "TKG3d.lib")
#pragma comment(lib, "TKGeomBase.lib")
#pragma comment(lib, "TKGeomAlgo.lib")
void makeSurface(Handle(Geom_BSplineSurface)& theSurface)
{
    TColgp_Array2OfPnt aPoints(1, 5, 1, 5);
    aPoints.SetValue(1, 1, gp_Pnt(-4, -4, 5));
    aPoints.SetValue(1, 2, gp_Pnt(-4, -2, 5));
    aPoints.SetValue(1, 3, gp_Pnt(-4, 0, 4));
    aPoints.SetValue(1, 4, gp_Pnt(-4, 2, 5));
    aPoints.SetValue(1, 5, gp_Pnt(-4, 4, 5));
    aPoints.SetValue(2, 1, gp_Pnt(-2, -4, 4));
    aPoints.SetValue(2, 2, gp_Pnt(-2, -2, 4));
    aPoints.SetValue(2, 3, gp_Pnt(-2, 0, 4));
    aPoints.SetValue(2, 4, gp_Pnt(-2, 2, 4));
    aPoints.SetValue(2, 5, gp_Pnt(-2, 5, 4));
    aPoints.SetValue(3, 1, gp_Pnt(0, -4, 3.5));
    aPoints.SetValue(3, 2, gp_Pnt(0, -2, 3.5));
    aPoints.SetValue(3, 3, gp_Pnt(0, 0, 3.5));
    aPoints.SetValue(3, 4, gp_Pnt(0, 2, 3.5));
    aPoints.SetValue(3, 5, gp_Pnt(0, 5, 3.5));
    aPoints.SetValue(4, 1, gp_Pnt(2, -4, 4));
    aPoints.SetValue(4, 2, gp_Pnt(2, -2, 4));
    aPoints.SetValue(4, 3, gp_Pnt(2, 0, 3.5));
    aPoints.SetValue(4, 4, gp_Pnt(2, 2, 5));
    aPoints.SetValue(4, 5, gp_Pnt(2, 5, 4));
    aPoints.SetValue(5, 1, gp_Pnt(4, -4, 5));
    aPoints.SetValue(5, 2, gp_Pnt(4, -2, 5));
    aPoints.SetValue(5, 3, gp_Pnt(4, 0, 5));
    aPoints.SetValue(5, 4, gp_Pnt(4, 2, 6));
    aPoints.SetValue(5, 5, gp_Pnt(4, 5, 5));
    theSurface = GeomAPI_PointsToBSplineSurface(aPoints).Surface();
}
void writeStl(const IntPatch_Polyhedron& thePolyhedron, const std::string& theFileName)
{
    // Dump surface polyhedron to STL file.
    std::ofstream aStlFile(theFileName);
    aStlFile << "solid polyhedron" << std::endl;
    // Dump triangles.
    for (Standard_Integer t = 1; t <= thePolyhedron.NbTriangles(); ++t)
    {
        Standard_Integer aPi1 = 0;
        Standard_Integer aPi2 = 0;
        Standard_Integer aPi3 = 0;
        thePolyhedron.Triangle(t, aPi1, aPi2, aPi3);
        const gp_Pnt& aP1 = thePolyhedron.Point(aPi1);
        const gp_Pnt& aP2 = thePolyhedron.Point(aPi2);
        const gp_Pnt& aP3 = thePolyhedron.Point(aPi3);
        aStlFile << "facet" << std::endl;
        aStlFile << "outer loop" << std::endl;
        aStlFile << "vertex " << aP1.X() << " " << aP1.Y() << " " << aP1.Z() << std::endl;
        aStlFile << "vertex " << aP2.X() << " " << aP2.Y() << " " << aP2.Z() << std::endl;
        aStlFile << "vertex " << aP3.X() << " " << aP3.Y() << " " << aP3.Z() << std::endl;
        aStlFile << "endloop" << std::endl;
        aStlFile << "endfacet" << std::endl;
    }
    aStlFile << "endsolid polyhedron" << std::endl;
    aStlFile.close();
}
void testPolyhedron()
{
    // Plane surface polyhedron.
    Handle(Geom_Plane) aPlane = new Geom_Plane(gp::XOY());
    Handle(GeomAdaptor_Surface) aSurfaceAdaptor = new GeomAdaptor_Surface(aPlane, 0.0, 10.0, 0.0, 20.0);
    IntPatch_Polyhedron aPlanePolyhedron(aSurfaceAdaptor);
    writeStl(aPlanePolyhedron, "d:/plane.stl");
    // Spherical surface polyhedron.
    Handle(Geom_SphericalSurface) aSphericalSurface = new Geom_SphericalSurface(gp::XOY(), 3.0);
    aSurfaceAdaptor = new GeomAdaptor_Surface(aSphericalSurface);
    IntPatch_Polyhedron aSphericalPolyhedron(aSurfaceAdaptor);
    writeStl(aSphericalPolyhedron, "d:/spherical.stl");
    // Cylindrical surface polyhedron.
    Handle(Geom_CylindricalSurface) aCylindricalSurface = new Geom_CylindricalSurface(gp::XOY(), 5.0);
    aSurfaceAdaptor = new GeomAdaptor_Surface(aCylindricalSurface, 0.0, M_PI, 0.0, 8.0);
    IntPatch_Polyhedron aCylindricalPolyhedron(aSurfaceAdaptor);
    writeStl(aCylindricalPolyhedron, "d:/cylindrical.stl");
    // Toroidal Surface polyhedron.
    Handle(Geom_ToroidalSurface) aToroidalSurface = new Geom_ToroidalSurface(gp::XOY(), 10.0, 3.0);
    aSurfaceAdaptor = new GeomAdaptor_Surface(aToroidalSurface);
    IntPatch_Polyhedron aToroidalPolyhedron(aSurfaceAdaptor);
    writeStl(aToroidalPolyhedron, "d:/toroidal.stl");
    // BSpline surface polyhedron.
    Handle(Geom_BSplineSurface) aBSplineSurface;
    makeSurface(aBSplineSurface);
    aSurfaceAdaptor = new GeomAdaptor_Surface(aBSplineSurface);
    IntPatch_Polyhedron aPolyhedron(aSurfaceAdaptor);
    writeStl(aPolyhedron, "d:/bspline.stl");
}
int main(int argc, char* argv[])
{
    testPolyhedron();
    return 0;
}