Topology and Geometry in OpenCascade-Topology

eryar@163.com

摘要Abstract：本文簡要介紹了幾何造型中的邊界表示法（BRep），并結(jié)合程序說明OpenCascade中的邊界表示的具體實現(xiàn)，即拓樸與幾何的聯(lián)系。對具有幾何信息的拓樸結(jié)構(gòu)頂點（vertex）、邊（edge）、面（face）進(jìn)行了詳細(xì)說明。本文通過ACIS與OpenCascade進(jìn)行對比來對拓樸（Topology）的概念進(jìn)行說明。并通過示例程序，說明如何在OpenCascade中取得與一個拓樸對象相連的其他拓樸對象，包括父對象和子對象。

關(guān)鍵字Key Words：OpenCascade、ACIS、BRep、Topology、Geometry

一、引言 Introduction

邊界表示（Boundary Representation）也稱為BRep表示，它是幾何造型中最成熟、無二義的表示法。實體的邊界通常是由面的并集來表示，而每個面又由它所在的曲面的定義加上其邊界來表示，面的邊界是邊的并集，而邊又是由點來表示的。

邊界表示的一個重要特征是描述形體的信息包括幾何信息（Geometry）和拓樸信息（Topology）兩個方面。拓樸信息描述形體上的頂點、邊、面的連接關(guān)系，它形成物體邊界表示的“骨架”。形體的幾何信息猶如附著在“骨架”上的肌肉。例如，形體的某個面位于某一個曲面上，定義這一曲面方程的數(shù)據(jù)就是幾何信息。此外，邊的形狀、頂點在三維空間中的位置（點的坐標(biāo)）等都是幾何信息，一般來說，幾何信息描述形體的大小、尺寸、位置和形狀等。

在邊界表示法中，邊界表示就按照體－面－環(huán)－邊－點的層次，詳細(xì)記錄構(gòu)成形體的所有幾何元素的幾何信息及其相互連接的拓樸關(guān)系。這樣，在進(jìn)行各種運算和操作中，就可以直接取得這些信息。

拓樸是指一個模型中的不同實體之間的關(guān)系，它描述了幾何實體之間的連接方式。拓樸定義了一個空間位置不固定的浮動模型。當(dāng)拓樸實體與幾何信息關(guān)聯(lián)在一起時，它的空間位置才確定。

拓樸可以是有邊界的、沒邊界的和半封閉的，它允許實體是完全實體，也可以是不完全實體。例如，實體可以沒有面，面可以沒有邊，實體也可以從內(nèi)部將它分割成殼的內(nèi)部面。這種實體在物理世界中是不存在的，但在幾何造型內(nèi)核中可以表現(xiàn)出來。

二、ACIS中的拓樸結(jié)構(gòu) Topology of ACIS

ACIS模型的邊界表示（B-Rep）是將模型的拓樸結(jié)構(gòu)按層次分解成下述對象：

1. 體（Body）：是實體對象的最高層次，是塊（lump）的集合。體可以是線、面、或?qū)嵭捏w；

2. 塊（Lump）：空間一維、二維或三維點連接而成的集合，與其他塊（lump）不關(guān)聯(lián)，其邊界由殼（shell）組成；

3. 殼（Shell）：互聯(lián)的線或面的集合，它可以界定實體的外部或內(nèi)部區(qū)域；

4. 子殼（Subshell）：殼的進(jìn)一步分解，用于處理內(nèi)部處理算法的效率；

5. 面（Face）：被一個或多個邊（edge）組成的環(huán)（loop）界定的曲面中的連通域。面可以是“雙向”的，這時它的厚度趨于無窮小。面也可以是“單向”的，這時面的法線指向面的外部，另一邊側(cè)是面的內(nèi)部；

6. 環(huán)（Loop）：面（face）的邊界中互相連接的部分，它由一系列的有向邊（coedge）組成。通常環(huán)是封閉的，沒有實際的開始和結(jié)束點，但是ACIS中的環(huán)可以是開環(huán)；

7. 線（Wire）：沒有附著在面上的，連接在一起的有向邊（coedge）；

8. 有向邊（Coedge）：表示面（face）或線（wire）中對某個邊的引用；

9. 邊（Edge）：與曲線關(guān)聯(lián)的拓樸，由頂點（vertex）界定。

10. 頂點（Vertex）：點是幾何造型中的最基本元素。用計算機(jī)存儲、管理、輸出形體的實質(zhì)就是對點集及其連接關(guān)系的處理。

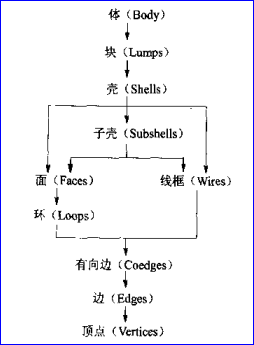
Figure 2.1 Topology of ACIS

上圖說明了概念上的拓樸對象之間的關(guān)系，這些對象組成了ACIS邊界表示方法的基礎(chǔ)。它們在ACIS中分別用類BODY、LUMP、SHELL、SUBSHELL、FACE、LOOP、WIRE、COEDGE、EDGE和VERTEX實現(xiàn)，這些類派生于類ENTITY。

ACIS通過在它的數(shù)據(jù)結(jié)構(gòu)中整合了線框、曲面和實體這三種表示方法，將這三種不同的幾何體聯(lián)系在一起。線框?qū)嶓w可以和實體（solid）與面實體共享，它們可以是共享邊、有向邊與頂點。由于這種共存的實現(xiàn)，使ACIS具有了表示混合維度模型與各種各樣不封閉模型的能力，如一個平面可以只在3個方向上有邊界邊，另外一方向沒有邊界。

Figure 2.2 Class Diagram of ACIS Topology

ACIS的對象都有包圍盒（Bound），這在求交運算中很有用，可以提高效率。如果兩個對象的包圍盒相交，那么這兩個對象則可能相交，然后再執(zhí)行更精確的求交運算。如果兩個對象的包圍盒不相交，則這兩個對象一定不相交，這樣進(jìn)一步的精確求交運算就不需要了。

既然拓樸表示了各對象之間的連接關(guān)系，那么給定一個對象時，可以容易得到其相連接其它對象。圖3說明了ACIS中組成實體、面、線和混合體的所有實體類，這些類及其方法提供了一個邊界表示造型器所必需的數(shù)據(jù)和方法。層次關(guān)系中向上和向下的指示說明這些類之間允許數(shù)據(jù)的快速切換，利用這種功能就可以確定兩個實體是否共享邊或頂點。從圖中可以看出拓樸類都有指向?qū)?yīng)的幾何體類的指針。

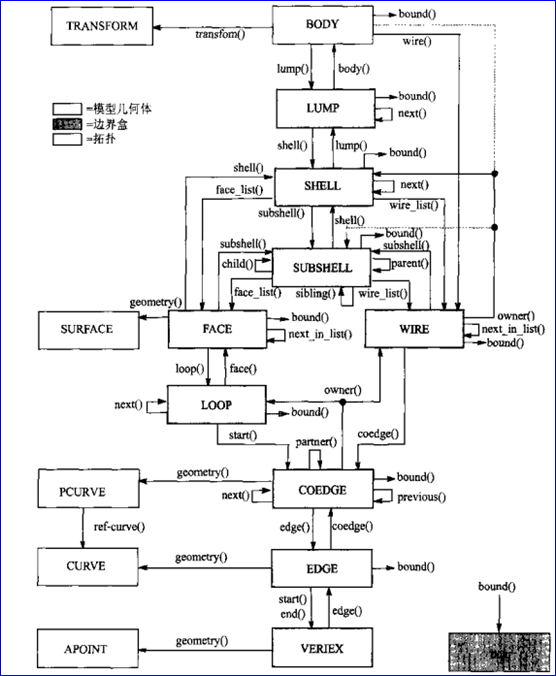
Figure 2.3 Topology structure of ACIS

從上圖可以看出，任意給定一個對象，可以快速獲得與其相連的其它對象，不管是向下還是向上。如給定一個FACE對象，可以通過loop()向下獲得LOOP對象；可以通過shell()向上獲得SHELL對象。

除了頂點以外，其他拓樸對象都有bound()，可以取得其包圍盒。

下面是統(tǒng)計一個模型中所有面的數(shù)量的程序，該程序就是利用拓樸類的公共成員函數(shù)來完成面的統(tǒng)計功能。通過這個程序來說明函數(shù)的使用方法。

三、OpenCascade中的拓樸結(jié)構(gòu) Topology of OpenCascade

3.1 OpenCascade拓樸簡介 Introduction of OpenCascade Topology

OpenCascade中的拓樸（topology）是根據(jù)STEP標(biāo)準(zhǔn)ISO-10303-42設(shè)計的。也許讀一下這個標(biāo)準(zhǔn)中的有關(guān)概念還是很有幫助的。STEP ISO-10303-42的相關(guān)資源：

http://www.steptools.com/support/stdev_docs/express/step_irs/index.html

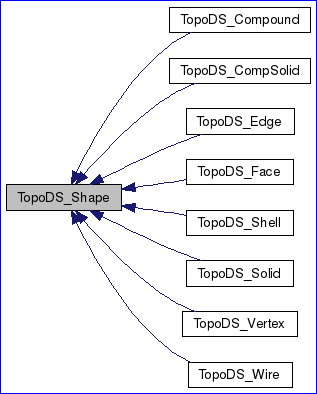
Figure 3.1 Topology data structure in OpenCascade

TopoDS_Shape由值控制，包含三個成員變量：myLocation、myOrient、myTShape。

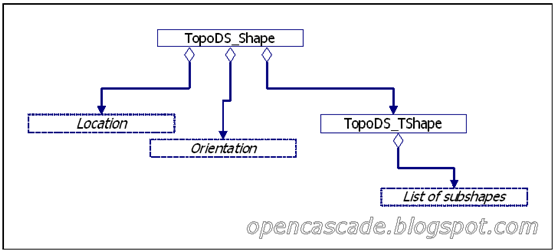
Figure 3.2 TopoDS_Shape member fields

其中TopoDS_TShape中包含與此對象相連接的子對象。

下圖所示為由一條邊連接的兩個面組成的殼（shell）：

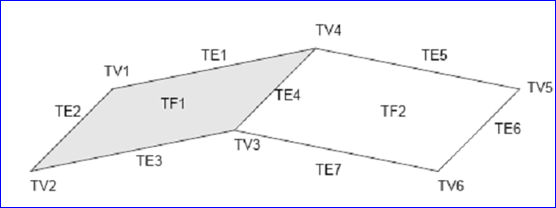
Figure 3.3 Structure of a shell formed from two faces

上圖所示的形狀表示為TS， 面TF1和TF2，有七條邊TE1~TE7和六個頂點TV1~TV6。

環(huán)TW1引用邊TE1~TE4；環(huán)TW2引用TE4~TE7 。邊引用的頂點如下：TE1（TV1，TV4），TE2（TV1，TV2），TE3（TV2，TV3），TE4（TV3，TV4），TE5（TV4，TV5），TE6（TV5，TV6），TE7（TV3，TV6）。

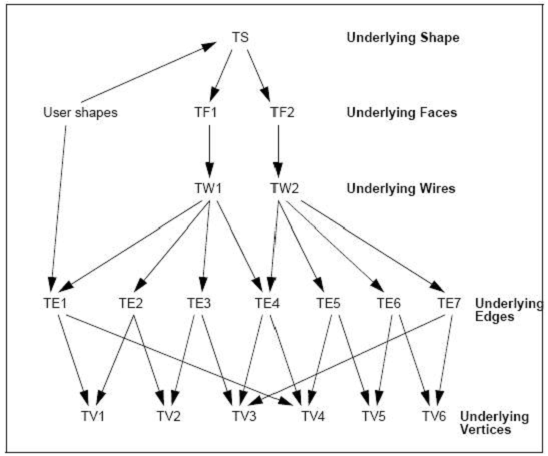
Figure 3.4 Data structure of the shell formed from two faces connected at an edge

注：OpenCascade中的這個數(shù)據(jù)結(jié)構(gòu)中不包含“反向引用（back references）”，即所有的引用只從復(fù)雜形狀到簡單形狀。（Note that this data structure does not contain any “back references”. All references go from more comples underlying shapes to less complex ones.）有點有向圖的意思。

這個根據(jù)OpenCascade的拓樸結(jié)構(gòu)的類圖可知，訪問形狀的子對象是很容易的。為了獲得一個對象的拓樸，不管是向上還是向下，OpenCascade提供了專門類和函數(shù)來實現(xiàn)。當(dāng)向下訪問拓樸對象時，OpenCascacde提供了兩種方法來遍歷子對象。向上遍歷時，OpenCascade提供了一個靜態(tài)函數(shù)TopExp::MapShapesAndAncestors()來實現(xiàn)。以下分別對其進(jìn)行說明。

3.2 遍歷子對象 Iteration over Children

遍歷子對象是向下來訪問拓樸關(guān)系。OpenCascade中遍歷一個形狀的子對象的兩個方法分別為：

l 直接使用類TopoDS_Iterator來遍歷：

Direct children can be retrieved using TopoDS_Iterator，如下函數(shù)可以訪問當(dāng)前對象所有的子對象，不管子對象的類型。通過遞歸的方式來實現(xiàn)。

TopoDS_Iterator有兩個標(biāo)志位，用于控制在查詢子對象時設(shè)定是否考慮父對象的位置和朝向（location and orientation）。若位置（location）標(biāo)志設(shè)置為開，那么所有子對象返回的值就像它們是獨立的對象一樣，而且位置是在具有全局坐標(biāo)系的三維空間中的位置。（例如用戶將看到單獨取出來的邊edge與其父對象環(huán)wire中顯示的位置是一樣的。）若朝向（orientation）標(biāo)設(shè)置為開，則返回的子對象的朝向?qū)兂筛笇ο蟮某蚺c子對象朝向的乘積（例如，子對象和父對象兩者都是反向reversed或是向前forward，則結(jié)果仍然向前。向前與反向的任意組合結(jié)果都將為反向）。

若標(biāo)志位為關(guān)，則子對象就只返回其自身保存的位置和朝向。默認(rèn)情況下，兩個標(biāo)志位都設(shè)置為開。

l 使用類TopExp_Explorer來遍歷指定類型的子對象：

若只想訪問形狀指定類型的子對象，可以使用類TopExp_Explorer來實現(xiàn)。如下程序所示為訪問對象的邊的功能。

類TopExp_Explorer還有一個附加參數(shù)，可以用來指定要跳過的父對象類型。這個參數(shù)在下面的情況下很有用。例如只想取得“懸空”邊（floating edge, 即不屬于面的邊），就可用下面代碼來實現(xiàn)：

3.3 反向引用 Back references

在使用OpenCascade時，你可能也注意到了，或者根據(jù)類圖分析到拓樸對象包含其子對象，而不是相反的方式。這是可以理解的，同一個對象或者子對象可以屬于不同的對象。例如任意共享邊可以屬于至少兩個面。然而有時也需要從子對象追蹤到與其相連的父對象。在OpenCascade中提供了靜態(tài)函數(shù)TopExp::MapShapesAndAncestors()來實現(xiàn)這個功能。

上面的代碼生成了myShape中面和邊之間的映射。若myShape是長方體，每一條邊會映射到兩個面上。若遍歷同樣的長方體，并在每一個面中盡力找到邊的父對象，那么明顯的該映射中一條邊只有一個面，也就是當(dāng)前正在搜索的面。

四、示例程序 Example Code

1. 統(tǒng)計一個長方體面的數(shù)量

程序輸出結(jié)果為：

2. 反向訪問

程序輸出結(jié)果：

五、結(jié)論 Conclusion

OpenCascade中的拓樸關(guān)系不像ACIS中那樣直接，但是也提供了向下訪問子形狀、向上訪問父形狀的類和函數(shù)，使用起來要涉及到好幾個類，不是很方便。

當(dāng)向上訪問與頂點相連接的邊時，有重復(fù)數(shù)據(jù)。

六、參考資料 References

1. Roman Lygin, OpenCascade notes, opencascade.blogspot.com

2. 詹海生等, 基于ACIS的幾何造型技術(shù)與系統(tǒng)開發(fā), 清華大學(xué)出版社, 2002

3. 孫家廣等. 計算機(jī)圖形學(xué). 清華大學(xué)出版社

4. OpenCascade source code.