Topology and Geometry in OpenCascade-Face
eryar@163.com
摘要Abstract：本文簡(jiǎn)要介紹了幾何造型中的邊界表示法（BRep），并結(jié)合程序說明OpenCascade中的邊界表示的具體實(shí)現(xiàn)，即拓樸與幾何的聯(lián)系。對(duì)具有幾何信息的拓樸結(jié)構(gòu)頂點(diǎn)（vertex）、邊（edge）、面（face）進(jìn)行了詳細(xì)說明。本文僅對(duì)面（Face）進(jìn)行說明。
關(guān)鍵字Key Words：OpenCascade、BRep、Topology、Geometry、Face
一、引言 Introduction
面（Face）由一個(gè)外環(huán)和若干個(gè)內(nèi)環(huán)來表示，內(nèi)環(huán)完全在外環(huán)之內(nèi)。根據(jù)環(huán)（Wire）的定義，在面上沿環(huán)的方向前進(jìn)，左側(cè)總在面內(nèi)，右側(cè)總在面外。面有方向性，一般用其外法矢方向作為該面的正向。若一個(gè)面的法矢向外，稱為正向面；反之，稱為反向面。面的形狀（surface）由面的幾何信息來表示，可以是平面或曲面，平面可用平面方程來描述，曲面可以用控制多邊形或型值點(diǎn)來描述（NURBS曲面），也可用曲面方程（隱式、顯式或參數(shù)形式）來描述。對(duì)于參數(shù)曲面，通常在其二維參數(shù)域上定義環(huán)，這樣就可以由一些二維的有向邊來表示環(huán)，集合運(yùn)算中對(duì)面的分割也可在二維參數(shù)域上進(jìn)行。
OpenCascade中的面結(jié)構(gòu)如下圖所示：
Figure 1.1 OpenCascade Face
根據(jù)其類圖可知，面除了其參數(shù)曲面mySurface外，還包含顯示曲面的剖分（由三角形組成）。當(dāng)面在著色顯示模式下時(shí)會(huì)計(jì)算出面的三角形。可視化的算法是由BRepMesh::Mesh()來為每個(gè)面三角剖分后用來顯示。
二、面 Face
面（Face）是用來描述三維實(shí)體邊界的拓樸實(shí)體。面是由底層的曲面及一個(gè)或多個(gè)環(huán)（Wire）來描述。例如，一個(gè)圓柱體包含三個(gè)面：底面、頂面和側(cè)面。每個(gè)面都是無限的（無界的）（Geom_Plane和Geom_CylindricalSurface），通過邊界來限定無限的面得到面。即用位于Geom_Circle上的邊形成的環(huán)，限定出底面和頂面。側(cè)面包含四條邊：其中兩條邊與頂面和底面其享，剩下的兩條邊是縫合邊（seam edge），參看之前的討論。限定側(cè)面的環(huán)包含縫合邊兩次，兩個(gè)縫合邊具有不同的朝向。
2.1 曲面 Surface
讓我們簡(jiǎn)要回顧一下什么是曲面（surface）。如果你在高中時(shí)學(xué)過數(shù)學(xué)分析（mathematical analysis），那么你可能對(duì)這個(gè)概念已經(jīng)熟記于心。如果沒學(xué)過，那么可能需要讀些文章來自學(xué)。在wikipedia上有關(guān)于參數(shù)曲面的簡(jiǎn)單例子。
曲面將二維參數(shù)空間{u, v}映射到三維空間。如下圖所示：
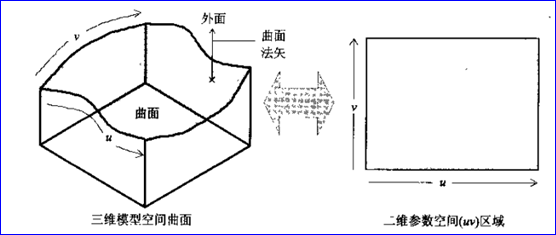
Figure 2.1 Map parameter space{u, v} into 3D space
參數(shù)區(qū)間可以有界，也可以是無界的，也可以只在一個(gè)方向上有界。如平面（Plane）的參數(shù)空間是無界的；NURBS是有界的；圓柱面（Cylindrical Surface）在U方向上有界（U∈[0，2π]），在V方向上是無界的。
Geom_Surface::Value()返回一個(gè)對(duì)應(yīng)于參數(shù)空間中的參數(shù)（U，V）的空間點(diǎn)（X，Y，Z）。例如：地球上的任意一點(diǎn)都由緯度（V）和經(jīng)度（U）表示，但是在世界坐標(biāo)系中可以看作三維點(diǎn)（假如地球的中心定義為原點(diǎn)）。這個(gè)函數(shù)是純虛函數(shù)，所有派生自Geom_Surface的類都有對(duì)這個(gè)函數(shù)的實(shí)現(xiàn)，使計(jì)算各種曲面上對(duì)應(yīng)參數(shù)的空間點(diǎn)的方式統(tǒng)一。
讓我們回想一下，邊必須具有三維曲線（3D Curve）和曲面空間中的參數(shù)曲線（pcurve）。而OpenCascade要求面的邊界（環(huán)wire）在三維和二維空間中必須是閉合的。因此，圓柱的側(cè)面是采用前面我們討論的那樣來描述的。
2.2 朝向 Orientation
面的朝向表示面的法向與曲面法向之間的關(guān)系（Face orientation shows how face normal is aligned with its surface normal）。若面的朝向是TopAbs_FORWARD（向前），則面的法向與曲面的法向一致；若面的朝向是TopAbs_REVERSED（反向），則面的法向與曲面的法向相反。面的法向表示材質(zhì)的位置，材料位于面的背面。在正確描述的實(shí)體中，所有面的法向都是向外的，如下圖所示：
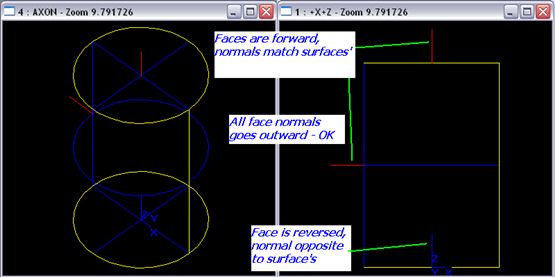
Figure 2.2 In a correct solid body all face normals go outward
面上的材料是由邊的朝向確定的。方向是由曲面不是面（）的法向和邊的微分的叉積確定。若邊的朝向向前，則邊的導(dǎo)數(shù)等于它的三維曲線的導(dǎo)數(shù)；若邊的朝向反向，則邊的導(dǎo)數(shù)與它的三維曲線的導(dǎo)數(shù)相反。也許考慮邊的參數(shù)曲線會(huì)更易于理解：假如邊是向前的，材料在它的左側(cè)，假如是反向的，則材料在它的右側(cè)。這讓我想起了格林公式中對(duì)平面區(qū)域的邊界曲線正向的規(guī)定：對(duì)平面區(qū)域D的邊界曲線L，我們規(guī)定L的正向如下：當(dāng)觀察者沿L的這個(gè)方向行走時(shí)，D內(nèi)在他附近處的那一部分總在他的左邊。
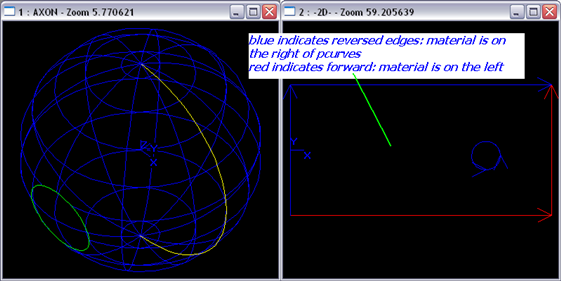
Figure 2.3 Orientation of the edge
當(dāng)用積分區(qū)域的概念來理解邊的朝向時(shí)好像要容易些。把參數(shù)空間看作積分區(qū)域D，其中藍(lán)色的邊表示材料在參數(shù)曲線的右側(cè)；紅色的邊表示材料在邊的左側(cè)。
2.3 容差 Tolerance
面的容差的幾何意義是包圍面的一個(gè)具有厚度的板。如下圖所示：
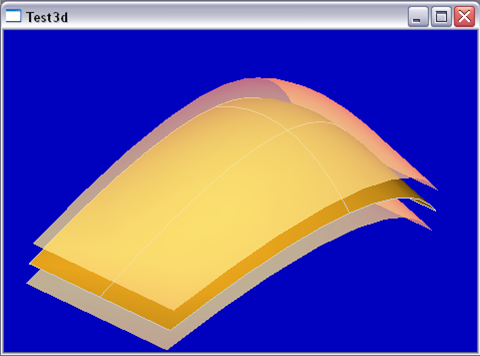
Figure 2.4 Face Tolerance
與邊和頂點(diǎn)的容差相比，建模算法中用到面的容差的情況相對(duì)要少。通常都使用默認(rèn)值Precision::Confusion()。通常情況下，OpenCascade要求注意以下條件：
當(dāng)邊位于面上，頂點(diǎn)位于邊上時(shí)，面的容差<=邊的容差<=頂點(diǎn)的容差。
2.4 三角剖分 Triangulation
除了面的參數(shù)表示，為了面的顯示，需要對(duì)面進(jìn)行三角剖分，剖分得到的三角形也保存在面的數(shù)據(jù)結(jié)構(gòu)中。當(dāng)在著色渲染模式下時(shí)，可視化算法內(nèi)部調(diào)用了BRepMesh::Mesh()來對(duì)每個(gè)面進(jìn)行三角剖分，并將三角剖分得到的三角形加到面的數(shù)據(jù)結(jié)構(gòu)中。
2.5 附加位置 Additional location
與邊和頂點(diǎn)不同，面有附加位置信息（TopLoc_Location），它是面（BRep_TFace）的成員變量。所以，在使用底層曲面或三角剖分得到的三角形時(shí)，不要忘了將其考慮進(jìn)去。
三、示例程序 Example Code
3.1 底層創(chuàng)建面并訪問其數(shù)據(jù) Creating a face bottom-up and accessing the data
與創(chuàng)建邊和頂點(diǎn)一樣，需要類BRep_Builder和Brep_Tool來從底層創(chuàng)建面和訪問面中的數(shù)據(jù)。代碼如下所示：
1 BRep_Builder aBuilder;
2 TopoDS_Face aFace;
3
4 aBuilder.MakeFace (aFace, aSurface, Precision::Confusion());
5
6 
7
8 TopLoc_Location aLocation;
9 Handle(Geom_Surface) aSurf = BRep_Tool::Surface (aFace, aLocation);
10
11 gp_Pnt aPnt = aSurf->Value (aU, aV).Transformed (aLocation.Transformation());
12
13 //or to transform a surface at once
14 //Handle(Geom_Surface) aSurf = BRep_Tool::Surface (aFace);
15 //gp_Pnt aPnt = aSurf->Value (aU, aV);
16 Handle(Poly_Triangulation) aTri = BRep_Tool::Triangulation (aFace, aLocation);
17
18 aPnt = aTri->Nodes.Value (i).Transformed (aLocation.Transformation());
19
20
一定要考慮面的附加位置信息。
四、結(jié)論 Conclusion
面是邊界表示法BRep中有幾何數(shù)據(jù)的最后一個(gè)拓樸結(jié)構(gòu)。為了面的顯示，需要對(duì)其進(jìn)行三角剖分，三角剖分后的數(shù)據(jù)也是保存在面的數(shù)據(jù)結(jié)構(gòu)中。面還有附加位置數(shù)據(jù)需要考慮，若不考慮附加位置，剖分后的三角形都是相對(duì)于原點(diǎn)的。
從底層創(chuàng)建面和訪問面的屬性數(shù)據(jù)，與頂點(diǎn)和邊一樣，使用類BRep_Builder和類BRep_Tool來實(shí)現(xiàn)。
五、參考資料
1. Roman Lygin, OpenCascade notes, opencascade.blogspot.com
2. 孫家廣等. 計(jì)算機(jī)圖形學(xué). 清華大學(xué)出版社
3. OpenCascade source code.