OpenCascade中網格的數據結構
Mesh Data Structure in OpenCascade
eryar@163.com
摘要Abstract:本文對網格數據結構作簡要介紹,并結合使用OpenCascade中的數據結構,將網格數據在OpenSceneGraph中可視化。
關鍵字KeyWords:OpenCascade、OpenSceneGraph、Triangulation、Mesh Data Structure
一、引言 Introduction
三角網格就是全部由三角形組成的多邊形網格。多邊形和三角網格在圖形學和建模中廣泛使用,用來模擬復雜物體的表面,如建筑、車輛、人體,當然,還有茶壺等自由曲面。任意多邊形網格都能轉換成三角網格。三角網格以其簡單性而吸引人,相對于一般多邊形網格許多操作對三角網格列容易。
常用的網格數據文件有:
1.Wavefront OBJ(*.obj)
2.3D Max(*.max, *.3ds)
3.VRML(*.vrl)
4.Inventor(*.iv)
5.PLY(*.ply, *.ply2)
6.STL(*.stl)
7.Off(*.off) in CGAL library
有些文件以文本方式保存,有些可以以二進制方式保存。如下圖所示為OBJ文件的格式:

Figure 1.1 Wavefront OBJ File Format
l Vertices
n 以‘V’開始;
n 其后為坐標值(x,y,z);
l Faces
n 以‘F’開始;
n 其后為面的頂點索引值;
l Other properties
n Normal, texture coordinates, material, etc.
二、三角網格的表示 Mesh Data Structure
三角網格為一個三角形列表,所以最直接的表示方法是用三角形數組:
struct Triangle
{
Vector3 p[3];
};
struct TriangleMesh
{
int triCount;
Triangle* triList;
};
對于某些應用程序,這種表示方法已經足夠。然而,術語“網格”隱含的相鄰三角形的連通性未在這種簡單表示中有任何體現。實際應用中出現的三角網格,每個三角形都和其他三角形共享邊。于是三角網格需要存儲三類信息:
l 頂點。每個三角形有三個頂點,各頂點都有可能和其他三角形共享;
l 邊。連接兩個頂點的邊,每個三角形有三條邊;
l 面。每個三角形對應一個面。我們可以用頂點或邊列表表示面;
根據應用程序的不同,有多種有效的網格表示方法。常用的一種標準的存儲格式為索引三角網格。
在索引三角網格中,我們維護了兩個列表:頂點表與三角形表。每個頂點包含一個3D位置,也可能有表面法向量、紋理映射坐標、光照值附加數據。每個三角形由頂點列表的三個索引值組成。通常頂點列出的順序是非常重要的,因為我們必須考慮面的“正面”和“反面”。從前面看時,我們將用順時針方向列出頂點。
在OpenCascade中,分別用類TColgp_Array1OfPnt和Poly_Array1OfTriangle表存儲頂點表和三角形表。注意到索引三角形列表中的鄰接信息是隱含的,即邊信息沒有存儲,但我們可以通過搜索三角形表找出公共邊。和前面“三角形數組”方式相比,這種方式確實能節省不少空間。原因是信息存于頂點級別,它的整數索引比之三角形數組里存儲的頂點重復率要小得多。實踐中,三角網里確實有大量的連接性問題。
簡單索引三角網格對于基本應用已經足夠了。但為更加高效地實現某些操作還可以進一步改進。主要的問題是鄰接信息沒有顯式表達,所以必須從三角形列表中搜索。另一種表達方法可以常數時間內取得這種信息。方法是顯式維護一個邊列表,每邊由兩個端點定義,同時維護一個共享該邊的三角形列表。這樣三角形可視為三條邊而非三個點的列表,也就是說它是邊列表的索引。該思想的一個擴展稱作“Winged Edge”模型(翼邊模型),對每一頂點,存儲使用該點的邊的索引。這樣三角形和邊都可以通過定位點列表快速查找。
大多數顯卡并不直接支持索引三角網。渲染三角形時,一般是將三個頂點同時提交。這樣,共享頂點會多次提交,三角形用到一次就提交一次。因為內存和圖形硬件間的數據傳輸是瓶頸,所以許多API和硬件支持特殊三角網格式以減少傳輸量。基本思想是排序點和面,使得顯存中已有的三角形不需要再次傳輸。
從最高靈活性到最低靈活性,我們討論三種方案:
n 頂點緩存;
n 三角帶Triangle Strip;
n 三角扇Triangle Fan;
三、程序示例 Code Example
在安裝好的CGAL庫中發現其例子中有很多off文件,其格式同常見的網格文件格式基本相同,結合OpenCascade和OpenSceneGraph,讀取off文件,將其表示的網格模型顯示出來。程序代碼如下所示:
1 /*
2 * Copyright (c) 2013 eryar All Rights Reserved.
3 *
4 * File : Main.cpp
5 * Author : eryar@163.com
6 * Date : 2013-08-10 18:02
7 * Version : V1.0
8 *
9 * Description : Mesh Viewer for the general mesh file format.
10 * Poly_Triangulation data structure can save vertices and triangle index.
11 *
12 */
13
14 // OpenSceneGraph library.
15 #include <osgDB/ReadFile>
16 #include <osgViewer/Viewer>
17 #include <osgGA/StateSetManipulator>
18 #include <osgViewer/ViewerEventHandlers>
19
20 #pragma comment(lib, "osgd.lib")
21 #pragma comment(lib, "osgDBd.lib")
22 #pragma comment(lib, "osgGAd.lib")
23 #pragma comment(lib, "osgViewerd.lib")
24
25 // OpenCascade library.
26 #include <TColgp_Array1OfPnt.hxx>
27 #include <Poly_Array1OfTriangle.hxx>
28 #include <Poly_Triangulation.hxx>
29
30 #pragma comment(lib, "TKernel.lib")
31 #pragma comment(lib, "TKMath.lib")
32
33 /**
34 * @breif Build the mesh from *.off file.
35 */
36 osg::Node* buildMesh(const std::string& fileName)
37 {
38 std::ifstream offFile(fileName.c_str());
39 std::string strBuffer;
40
41 osg::ref_ptr<osg::Geode> geode = new osg::Geode();
42 osg::ref_ptr<osg::Geometry> triGeom = new osg::Geometry();
43 osg::ref_ptr<osg::Vec3Array> vertices = new osg::Vec3Array();
44 osg::ref_ptr<osg::Vec3Array> normals = new osg::Vec3Array();
45
46 Standard_Integer nbNodes = 0;
47 Standard_Integer nbTriangles = 0;
48
49 // Ignore "OFF"
50 offFile>>strBuffer;
51 offFile>>nbNodes>>nbTriangles>>strBuffer;
52
53 TColgp_Array1OfPnt nodes(0, nbNodes);
54 Poly_Array1OfTriangle triangles(0, nbTriangles);
55
56 // Read node coordinate and store them.
57 Standard_Real dx = 0.0;
58 Standard_Real dy = 0.0;
59 Standard_Real dz = 0.0;
60
61 for (Standard_Integer i = 0; i < nbNodes; i++)
62 {
63 offFile>>dx>>dy>>dz;
64
65 nodes(i).SetCoord(dx, dy, dz);
66 }
67
68 // Read the triangles
69 Standard_Integer ni = 0;
70 Standard_Integer n1 = 0;
71 Standard_Integer n2 = 0;
72 Standard_Integer n3 = 0;
73
74 for (Standard_Integer i = 0; i < nbTriangles; i++)
75 {
76 offFile>>ni>>n1>>n2>>n3;
77
78 triangles(i).Set(n1, n2, n3);
79 }
80
81 // Construct the mesh data by Poly_Triangulation.
82 gp_Pnt node1;
83 gp_Pnt node2;
84 gp_Pnt node3;
85 Poly_Triangle triangle;
86 Handle_Poly_Triangulation T = new Poly_Triangulation(nodes, triangles);
87
88 for (Standard_Integer i = 0; i < nbTriangles; i++)
89 {
90 triangle = triangles.Value(i);
91
92 triangle.Get(n1, n2, n3);
93
94 node1 = nodes.Value(n1);
95 node2 = nodes.Value(n2);
96 node3 = nodes.Value(n3);
97
98 gp_XYZ vector12(node2.XYZ() - node1.XYZ());
99 gp_XYZ vector13(node3.XYZ() - node1.XYZ());
100 gp_XYZ normal = vector12.Crossed(vector13);
101 Standard_Real rModulus = normal.Modulus();
102
103 if (rModulus > gp::Resolution())
104 {
105 normal.Normalize();
106 }
107 else
108 {
109 normal.SetCoord(0., 0., 0.);
110 }
111
112 vertices->push_back(osg::Vec3(node1.X(), node1.Y(), node1.Z()));
113 vertices->push_back(osg::Vec3(node2.X(), node2.Y(), node2.Z()));
114 vertices->push_back(osg::Vec3(node3.X(), node3.Y(), node3.Z()));
115
116 normals->push_back(osg::Vec3(normal.X(), normal.Y(),normal.Z()));
117 }
118
119 triGeom->setVertexArray(vertices.get());
120 triGeom->addPrimitiveSet(new osg::DrawArrays(osg::PrimitiveSet::TRIANGLES, 0, vertices->size()));
121 triGeom->setNormalArray(normals);
122 triGeom->setNormalBinding(osg::Geometry::BIND_PER_PRIMITIVE);
123
124 geode->addDrawable(triGeom);
125
126 return geode.release();
127 }
128
129 int main(int argc, char* argv[])
130 {
131 osgViewer::Viewer myViewer;
132
133 std::string strFile;
134
135 (argc > 1) ? strFile = argv[1] : strFile = "ChineseDragon-10kv.off";
136
137 myViewer.setSceneData(buildMesh(strFile));
138
139 myViewer.addEventHandler(new osgGA::StateSetManipulator(myViewer.getCamera()->getOrCreateStateSet()));
140 myViewer.addEventHandler(new osgViewer::StatsHandler);
141 myViewer.addEventHandler(new osgViewer::WindowSizeHandler);
142
143 return myViewer.run();
144 }
程序效果圖如下所示:
Figure 3.1 ChineseDragon-10kv.off

Figure 3.2 Camel.off

Figure 3.3 cow.off
Figure 3.4 elephant.off
Figure 3.5 man.off
Figure 3.6 pinion.off
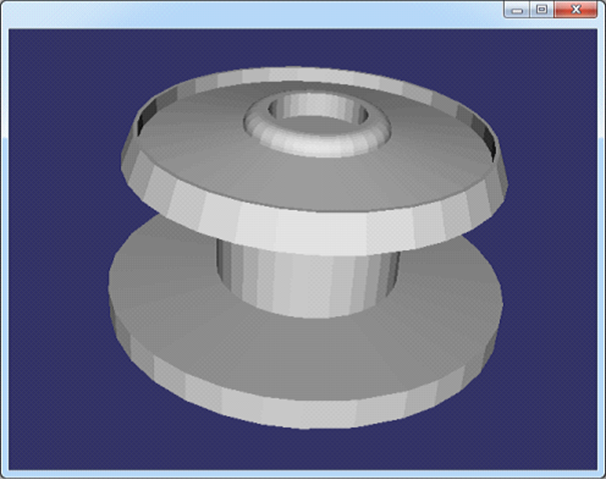
Figure 3.7 spool.off
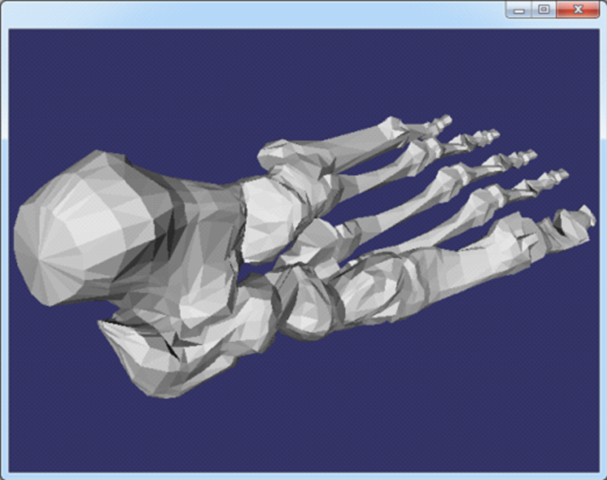
Figure 3.8 bones.off
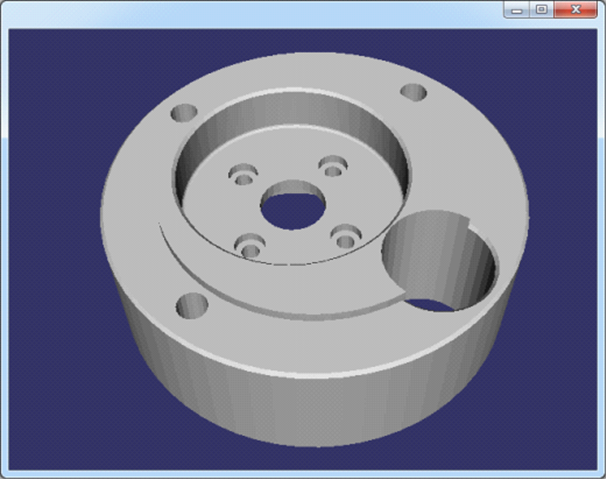
Figure 3.9 couplingdown.off
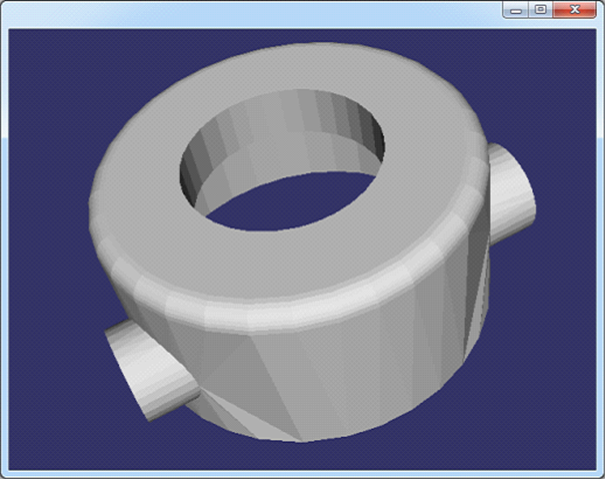
Figure 3.10 rotor.off
Figure 3.11 joint.off
Figure 3.12 knot1.off

Figure 3.13 anchor.off
Figure 3.14 mushroom.off
Figure 3.15 sphere.off
Figure 3.16 star.off
看到這些三維模型,很有感覺!在有關計算機圖形學的期刊上有可能也會看到上面的模型。
四、結論 Conclusion
三角網格在計算中用來近似表示三維模型。存儲三角網格的標準方式是使用索引三角網格方式。結合OpenCascade中的數據結構,將CGAL示例中的off文件在OpenSceneGraph中顯示出來,感覺很棒!