OpenCascade Law Function
eryar@163.com
1.Introduction
在OpenCASCADE的TKGeomAlgo Toolkit中提供了一個Law Package,在Law包中有一個基類:Law_Function,字面上翻譯為 規則函數。其類圖如下所示:
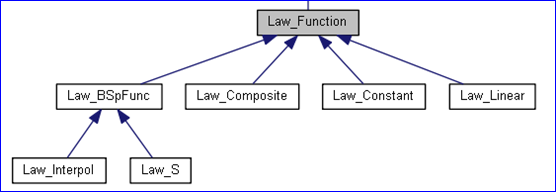
Figure 1. Law Function class diagram
本文主要對Law_Function的子類進行介紹,進一步理解OpenCASCADE中Law相關類的作用。
2.Law Functions
根據Law_Function可知,Law_Function的子類有常量規則Law_Constant、線性規則Law_Linear、組合規則Law_Composite及B樣條規則Law_BSpFunc。抽象類Law_Function的純虛函數有:
l Continuity(): 規則函數的連續性;
l Value():計算對應參數X的函數值Y;
l D1():計算規則函數在參數X處的一階導數;
l D2():計算規則函數在參數X處的二階導數;
l Bounds():規則函數的定義區間;

從上面的虛函數可以看出類Law_Function是一個一元變量的函數,與類math_Function的功能類似。
3.Test Code
下面的代碼將規則函數Law_Function的幾個子類通過生成Draw腳本,在Draw Test Harness中進行可視化,直觀地顯示出了幾個規則函數,便于理解。
/*
Copyright(C) 2018 Shing Liu(eryar@163.com)
Permission is hereby granted, free of charge, to any person obtaining a copy
of this software and associated documentation files(the "Software"), to deal
in the Software without restriction, including without limitation the rights
to use, copy, modify, merge, publish, distribute, sublicense, and / or sell
copies of the Software, and to permit persons to whom the Software is
furnished to do so, subject to the following conditions :
The above copyright notice and this permission notice shall be included in all
copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT.IN NO EVENT SHALL THE
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
SOFTWARE.
*/
#include <TColgp_Array1OfPnt2d.hxx>
#include <Law_Constant.hxx>
#include <Law_Linear.hxx>
#include <Law_BSpFunc.hxx>
#include <Law_S.hxx>
#include <Law_Interpol.hxx>
#pragma comment(lib, "TKernel.lib")
#pragma comment(lib, "TKMath.lib")
#pragma comment(lib, "TKG2d.lib")
#pragma comment(lib, "TKG3d.lib")
#pragma comment(lib, "TKGeomBase.lib")
#pragma comment(lib, "TKGeomAlgo.lib")
Standard_Integer aId = 0;
void draw(const Handle(Law_Function)& theLaw, std::ostream& theOutput)
{
const Standard_Integer aStep = 20;
Standard_Real aFirst = 0.0;
Standard_Real aLast = 0.0;
Standard_Real aDelta = 0.0;
Standard_Real aX = 0.0;
Standard_Real aY = 0.0;
theLaw->Bounds(aFirst, aLast);
aDelta = (aLast - aFirst) / aStep;
theOutput << "polyline law" << ++aId;
for (Standard_Integer i = 0; i <= aStep; ++i)
{
aX = aFirst + i * aDelta;
aY = theLaw->Value(aX);
theOutput << " " << aX << " " << aY << " 0.0";
}
theOutput << "\n vdisplay law" << aId << std::endl;
theOutput << "vaspects law" << aId << " -setColor " << ((aId % 2) ? " red " : " yellow ") << std::endl;
}
void test(std::ostream& theOutput)
{
// 1. Constant law.
Handle(Law_Constant) aConstantLaw = new Law_Constant();
aConstantLaw->Set(2.0, 0.0, 1.0);
draw(aConstantLaw, theOutput);
// 2. Linear evolution law.
Handle(Law_Linear) aLinearLaw = new Law_Linear();
aLinearLaw->Set(1.0, 2.0, 3.0, 5.0);
draw(aLinearLaw, theOutput);
// 3. An "S" evolution law.
Handle(Law_S) aSLaw = new Law_S();
aSLaw->Set(3.0, 5.0, 6.0, 8.0);
draw(aSLaw, theOutput);
// 4. Provides an evolution law that interpolates a set of parameter and value pairs (wi, radi)
TColgp_Array1OfPnt2d aPoints(1, 4);
aPoints.SetValue(1, gp_Pnt2d(6.0, 8.0));
aPoints.SetValue(2, gp_Pnt2d(7.0, 5.0));
aPoints.SetValue(3, gp_Pnt2d(8.0, 9.0));
aPoints.SetValue(4, gp_Pnt2d(9.0, 2.0));
Handle(Law_Interpol) anInterpolativeLaw = new Law_Interpol();
anInterpolativeLaw->Set(aPoints);
draw(anInterpolativeLaw, theOutput);
}
int main(int argc, char* argv[])
{
std::ofstream aTclFile("d:/tcl/law.tcl");
test(aTclFile);
return 0;
}
程序會在d:/tcl中生成一個law.tcl文件,將此文件加載到Draw 中即可顯示出規則函數對應的曲線,如下圖所示:
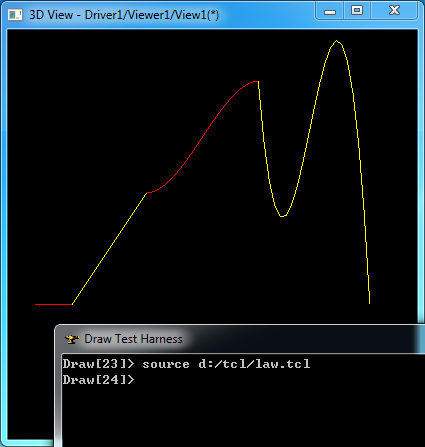
Figure 2. Visualization Law Function Curves
由圖可知,常量規則函數在定義區間內是一條直線;線性規則函數是一條直線;S型函數是S型的B樣條曲線;插值函數是根據指定點插值得到的B樣條曲線。
4.Conclusion
在OpenCASCADE中經常可以看到一些與Law相關的類,本文介紹了TKGeomAlgo中的Law包,綜上所述可知,Law就是一元函數,與math_Function的概念一致。
本文顯示規則曲線的方式可供借鑒,提高開發效率。只需要生成一個文本文件,就可以將結果可視化,對于其他三維的也是一樣。
為了方便大家在移動端也能看到我的博文和討論交流,現已注冊微信公眾號,歡迎大家掃描下方二維碼關注。
