久久播电影网,成人精品一区二区久久,久久中文字幕无码专区

Apply Newton Method to Find Extrema in OPEN CASCADE

Posted on 2015-12-06 10:47 eryar 閱讀(2521) 評論(0) 編輯收藏引用所屬分類: 2.OpenCASCADE

Apply Newton Method to Find Extrema in OPEN CASCADE

Abstract. In calculus, Newton’s method is used for finding the roots of a function. In optimization, Newton’s method is applied to find the roots of the derivative. OPEN CASCADE implement Newton method to find the extrema for a multiple variables function, such as find the extrema point for a curve and a surface.

Key Words. Nonlinear Programming, Newton Method, Extrema, OPEN CASCADE

1. Introduction

Newton法作為一種經(jīng)典的解無約束優(yōu)化問題的方法，在20世紀(jì)80~90年代發(fā)展起來的解線性規(guī)劃和凸規(guī)劃的內(nèi)點法中起到了重要作用。Newton法最初是Newton提出用于解非線性方程的，Newton曾用該法求解Kepler方程x-asinx=b，并得到精度很高的近似解。通過《OPEN CASCADE Multiple Variable Function》對OPEN CASCADE中多元函數(shù)的表達有了一個認(rèn)識。多元函數(shù)如何應(yīng)用的呢？下面提出一個問題及如何用程序來解決這個問題。對于任意給定的曲線和曲面，如何求出曲線和曲面上距離最近的點，假設(shè)曲線和曲面都是至少C2連續(xù)的。關(guān)于參數(shù)連續(xù)性可參考《OPEN CASCADE Curve Continuity》。如下圖所示：

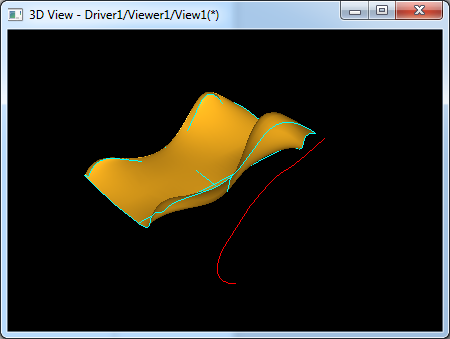
Figure 1.1 A Curve and A Surface

本文給出OPEN CASCADE中對此類問題的一種解法，即應(yīng)用Newton法求解非線性無約束多元函數(shù)的極值。學(xué)習(xí)如何將實際問題抽象成數(shù)學(xué)模型，從而使用數(shù)學(xué)的方法進行求解。

2.Construct Function

在實際應(yīng)用中，一個問題是不是可以表述為一個最優(yōu)化模型和怎么表示為一個最優(yōu)化模型，這是優(yōu)化方法是否可以應(yīng)用的前提，因而十分重要。但優(yōu)化問題的建模和其他數(shù)學(xué)問題的建模一樣，不屬于精確科學(xué)或數(shù)學(xué)的范疇，而是一項技術(shù)或技藝，沒有統(tǒng)一標(biāo)準(zhǔn)和方法。當(dāng)然建立的模型是否正確和模型的優(yōu)劣是可以通過實際效果來檢驗的。

OPEN CASCADE使用從math_MultipleVarFunctionWithHessian派生的一個具體類Extrema_GlobOptFuncCS來計算C2連續(xù)的曲線和曲面之間的距離的平方值。抽象出來的數(shù)學(xué)模型為：

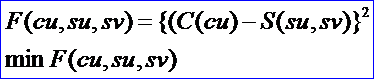
因為是從具有Hessian Matrix的多元函數(shù)派生，所以要求曲線曲面具有至少C2連續(xù)，即有至少有二階導(dǎo)數(shù)。且在類中分別實現(xiàn)計算函數(shù)值，計算一階導(dǎo)數(shù)值（梯度），計算二階導(dǎo)數(shù)值（Hessian Matrix）。計算函數(shù)值的代碼如下所示：

//======================================================================
//function : value
//purpose  :
//======================================================================
void Extrema_GlobOptFuncCS::value(Standard_Real cu,
                                  Standard_Real su,
                                  Standard_Real sv,
                                  Standard_Real &F)
{
  F = myC->Value(cu).SquareDistance(myS->Value(su, sv));
}

其中參數(shù)cu為參數(shù)曲線的參數(shù)，su,sv分別為參數(shù)曲面的參數(shù)。根據(jù)參數(shù)曲線曲面上的參數(shù)計算出相應(yīng)的點，然后計算出兩個點之間的距離的平方值即為函數(shù)值。與上述公式對應(yīng)。

根據(jù)多元函數(shù)一階導(dǎo)數(shù)（梯度）的定義，可得出梯度的計算公式如下：

計算梯度的代碼如下所示，從程序代碼可見程序就是上公式的具體實現(xiàn)。

//======================================================================
//function : gradient
//purpose  :
//======================================================================
void Extrema_GlobOptFuncCS::gradient(Standard_Real cu,
                                     Standard_Real su,
                                     Standard_Real sv,
                                     math_Vector &G)
{
  gp_Pnt CD0, SD0;
  gp_Vec CD1, SD1U, SD1V;

  myC->D1(cu, CD0, CD1);
  myS->D1(su, sv, SD0, SD1U, SD1V);

  G(1) = + (CD0.X() - SD0.X()) * CD1.X()
         + (CD0.Y() - SD0.Y()) * CD1.Y()
         + (CD0.Z() - SD0.Z()) * CD1.Z();
  G(2) = - (CD0.X() - SD0.X()) * SD1U.X()
         - (CD0.Y() - SD0.Y()) * SD1U.Y()
         - (CD0.Z() - SD0.Z()) * SD1U.Z();
  G(3) = - (CD0.X() - SD0.X()) * SD1V.X()
         - (CD0.Y() - SD0.Y()) * SD1V.Y()
         - (CD0.Z() - SD0.Z()) * SD1V.Z();
}

根據(jù)Hessian Matrix的定義，得到計算Hessian Matrix的公式如下：

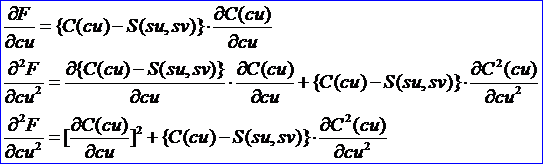
將函數(shù)積的求導(dǎo)法則應(yīng)用于求偏導(dǎo)數(shù)得到上述公式。同理求出Hessian Matrix的其他各項，如下公式所示：

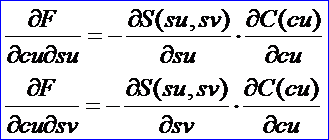
計算多元函數(shù)的二階導(dǎo)數(shù)Hessian Matrix的程序代碼如下所示：

//======================================================================
//function : hessian
//purpose  :
//======================================================================
void Extrema_GlobOptFuncCS::hessian(Standard_Real cu,
                                    Standard_Real su,
                                    Standard_Real sv,
                                    math_Matrix &H)
{
  gp_Pnt CD0, SD0;
  gp_Vec CD1, SD1U, SD1V, CD2, SD2UU, SD2UV, SD2VV;

  myC->D2(cu, CD0, CD1, CD2);
  myS->D2(su, sv, SD0, SD1U, SD1V, SD2UU, SD2VV, SD2UV);

  H(1,1) = + CD1.X() * CD1.X()
           + CD1.Y() * CD1.Y()
           + CD1.Z() * CD1.Z()
           + (CD0.X() - SD0.X()) * CD2.X()
           + (CD0.Y() - SD0.Y()) * CD2.Y()
           + (CD0.Z() - SD0.Z()) * CD2.Z();

  H(1,2) = - CD1.X() * SD1U.X()
           - CD1.Y() * SD1U.Y()
           - CD1.Z() * SD1U.Z();

  H(1,3) = - CD1.X() * SD1V.X()
           - CD1.Y() * SD1V.Y()
           - CD1.Z() * SD1V.Z();

  H(2,1) = H(1,2);

  H(2,2) = + SD1U.X() * SD1U.X()
           + SD1U.Y() * SD1U.Y()
           + SD1U.Z() * SD1U.Z()
           - (CD0.X() - SD0.X()) * SD2UU.X()
           - (CD0.Y() - SD0.Y()) * SD2UU.Y()
           - (CD0.Z() - SD0.Z()) * SD2UU.Z();

  H(2,3) = + SD1U.X() * SD1V.X()
           + SD1U.Y() * SD1V.Y()
           + SD1U.Z() * SD1V.Z()
           - (CD0.X() - SD0.X()) * SD2UV.X()
           - (CD0.Y() - SD0.Y()) * SD2UV.Y()
           - (CD0.Z() - SD0.Z()) * SD2UV.Z();

  H(3,1) = H(1,3);

  H(3,2) = H(2,3);

  H(3,3) = + SD1V.X() * SD1V.X()
           + SD1V.Y() * SD1V.Y()
           + SD1V.Z() * SD1V.Z()
           - (CD0.X() - SD0.X()) * SD2VV.X()
           - (CD0.Y() - SD0.Y()) * SD2VV.Y()
           - (CD0.Z() - SD0.Z()) * SD2VV.Z();
}

根據(jù)高階偏導(dǎo)數(shù)的定理可知，當(dāng)f(X)在點X0處所有二階偏導(dǎo)數(shù)連續(xù)時，那末在該區(qū)域內(nèi)這兩個二階混合偏導(dǎo)數(shù)必相等。所以Hessian Matrix為一個對稱矩陣，故

H(2,1)=H(1,2)

H(3,1)=H(1,3)

H(3,2)=H(2,3)

由此完成一個具有二階偏導(dǎo)數(shù)的多元函數(shù)的數(shù)學(xué)模型，用面向?qū)ο蟮姆绞角逦乇硎玖顺鰜怼：臀乙娺^的國內(nèi)一些程序相比，這種抽象思路還是很清晰，便于程序的理解和擴展。國內(nèi)有個圖形庫是C風(fēng)格的，一個函數(shù)幾千行，光函數(shù)參數(shù)就很多，參數(shù)名也很隨意，函數(shù)內(nèi)部變量名稱更是無法理解，什么i，j，k，ii，jj之類。這種程序別說可擴展，就是維護起來也是讓人頭疼的啊！

有了函數(shù)表達式，下面就是計算這個函數(shù)的極值了。

3.Newton’s Method

關(guān)于應(yīng)用Newton法計算一元非線性方程的根已經(jīng)在《OpenCASCADE Root-Finding Algorithm》中進行了說明，這里要學(xué)習(xí)下如何使用Newton法應(yīng)用于多元函數(shù)極值的計算。對于一元函數(shù)f(x)的求極值問題，當(dāng)f(x)連續(xù)可微時，最優(yōu)點x滿足f’(x)=0。于是當(dāng)f(x)二次連續(xù)可微時，求解f’(x)=0的Newton法為：

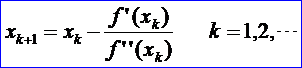
該方法稱為解無約束優(yōu)化問題的Newton方法。由《數(shù)學(xué)分析》可知，當(dāng)f(x)是凸函數(shù)時，f’(x)=0的解是minf(x)的整體最優(yōu)解。將Newton法擴展到多元函數(shù)的情況，也是利用二階Taylor級數(shù)將函數(shù)展開，得到多元函數(shù)的極值迭代公式：

關(guān)于多元函數(shù)Newton法公式的推導(dǎo)，可參考《最優(yōu)化方法》等書籍。Newton法的算法步驟如下：

A. 給定初始點，及精度；

B. 計算函數(shù)f(xk)的一階導(dǎo)數(shù)（梯度），二階導(dǎo)數(shù)（Hessian Matrix）：若|梯度|<精度，則停止迭代，輸出近似極小點；否則轉(zhuǎn)C；

C. 根據(jù)Newton迭代公式，計算x(k+1)；

OPEN CASCADE中Newton法計算極值的類是math_NewtonMinimum，可參考其代碼學(xué)習(xí)。下面給出前面提出的曲線曲面極值求解的實現(xiàn)代碼：

/*
*    Copyright (c) 2015 Shing Liu All Rights Reserved.
*
*           File : main.cpp
*         Author : Shing Liu(eryar@163.com)
*           Date : 2015-12-05 21:00
*        Version : OpenCASCADE6.9.0
*
*    Description : Learn Newton's Method for multiple variables
*                  function.
*/

#define WNT
#include <TColgp_Array1OfPnt.hxx>
#include <TColgp_Array2OfPnt.hxx>

#include <math_NewtonMinimum.hxx>

#include <GeomTools.hxx>
#include <BRepTools.hxx>

#include <GC_MakeSegment.hxx>

#include <GeomAdaptor_HCurve.hxx>
#include <GeomAdaptor_Surface.hxx>

#include <Extrema_GlobOptFuncCS.hxx>

#include <GeomAPI_PointsToBSpline.hxx>
#include <GeomAPI_PointsToBSplineSurface.hxx>

#include <BRepBuilderAPI_MakeEdge.hxx>
#include <BRepBuilderAPI_MakeFace.hxx>

#pragma comment(lib, "TKernel.lib")
#pragma comment(lib, "TKMath.lib")
#pragma comment(lib, "TKG2d.lib")
#pragma comment(lib, "TKG3d.lib")
#pragma comment(lib, "TKBRep.lib")
#pragma comment(lib, "TKGeomBase.lib")
#pragma comment(lib, "TKGeomAlgo.lib")
#pragma comment(lib, "TKTopAlgo.lib")

void testNewtonMethod(void)
{
    // approximate curve from the points
    TColgp_Array1OfPnt aCurvePoints(1, 5);
    aCurvePoints.SetValue(1, gp_Pnt(0.0, 0.0, -2.0));
    aCurvePoints.SetValue(2, gp_Pnt(1.0, 2.0, 2.0));
    aCurvePoints.SetValue(3, gp_Pnt(2.0, 3.0, 3.0));
    aCurvePoints.SetValue(4, gp_Pnt(4.0, 3.0, 4.0));
    aCurvePoints.SetValue(5, gp_Pnt(5.0, 5.0, 5.0));

    GeomAPI_PointsToBSpline aCurveApprox(aCurvePoints);

    // approximate surface from the points.
    TColgp_Array2OfPnt aSurfacePoints(1, 5, 1, 5);
    aSurfacePoints(1, 1) = gp_Pnt(-4,-4,5);
    aSurfacePoints(1, 2) = gp_Pnt(-4,-2,5);
    aSurfacePoints(1, 3) = gp_Pnt(-4,0,4);
    aSurfacePoints(1, 4) = gp_Pnt(-4,2,5);
    aSurfacePoints(1, 5) = gp_Pnt(-4,4,5);

    aSurfacePoints(2, 1) = gp_Pnt(-2,-4,4);
    aSurfacePoints(2, 2) = gp_Pnt(-2,-2,4);
    aSurfacePoints(2, 3) = gp_Pnt(-2,0,4);
    aSurfacePoints(2, 4) = gp_Pnt(-2,2,4);
    aSurfacePoints(2, 5) = gp_Pnt(-2,5,4);

    aSurfacePoints(3, 1) = gp_Pnt(0,-4,3.5);
    aSurfacePoints(3, 2) = gp_Pnt(0,-2,3.5);
    aSurfacePoints(3, 3) = gp_Pnt(0,0,3.5);
    aSurfacePoints(3, 4) = gp_Pnt(0,2,3.5);
    aSurfacePoints(3, 5) = gp_Pnt(0,5,3.5);

    aSurfacePoints(4, 1) = gp_Pnt(2,-4,4);
    aSurfacePoints(4, 2) = gp_Pnt(2,-2,4);
    aSurfacePoints(4, 3) = gp_Pnt(2,0,3.5);
    aSurfacePoints(4, 4) = gp_Pnt(2,2,5);
    aSurfacePoints(4, 5) = gp_Pnt(2,5,4);

    aSurfacePoints(5, 1) = gp_Pnt(4,-4,5);
    aSurfacePoints(5, 2) = gp_Pnt(4,-2,5);
    aSurfacePoints(5, 3) = gp_Pnt(4,0,5);
    aSurfacePoints(5, 4) = gp_Pnt(4,2,6);
    aSurfacePoints(5, 5) = gp_Pnt(4,5,5);

    GeomAPI_PointsToBSplineSurface aSurfaceApprox(aSurfacePoints);

    // construct the function.
    Handle_Adaptor3d_HCurve aAdaptorCurve = new GeomAdaptor_HCurve(aCurveApprox.Curve());
    Adaptor3d_Surface* aAdaptorSurface = new GeomAdaptor_Surface(aSurfaceApprox.Surface());

    Extrema_GlobOptFuncCS aFunction(&(aAdaptorCurve->Curve()), aAdaptorSurface);

    math_Vector aStartPoint(1, 3, 0.2);
    math_NewtonMinimum aSolver(aFunction, aStartPoint);
    aSolver.Perform(aFunction, aStartPoint);

    if (aSolver.IsDone())
    {
        aSolver.Dump(std::cout);
        math_Vector aLocation = aSolver.Location();

        gp_Pnt aPoint1 = aAdaptorCurve->Value(aLocation(1));
        gp_Pnt aPoint2 = aAdaptorSurface->Value(aLocation(2), aLocation(3));
        GC_MakeSegment aSegmentMaker(aPoint1, aPoint2);

        BRepBuilderAPI_MakeEdge anEdgeMaker(aSegmentMaker.Value());
        BRepTools::Write(anEdgeMaker.Shape(), "d:/tcl/min.brep");
    }

    GeomTools::Dump(aCurveApprox.Curve(), std::cout);
    GeomTools::Dump(aSurfaceApprox.Surface(), std::cout);

    BRepBuilderAPI_MakeEdge anEdgeMaker(aCurveApprox.Curve());
    BRepBuilderAPI_MakeFace aFaceMaker(aSurfaceApprox.Surface(), Precision::Approximation());

    BRepTools::Write(anEdgeMaker.Shape(), "d:/tcl/edge.brep");
    BRepTools::Write(aFaceMaker.Shape(), "d:/tcl/face.brep");

    // need release memory for the adaptor surface pointer manually.
    // whereas do not need release memory for the adaptor curve.
    // because it is mamanged by handle.
    delete aAdaptorSurface;
}

int main(int argc, char* argv[])
{
    testNewtonMethod();

    return 0;
}

上述代碼通過擬合點得到的任意一曲線和曲面，計算其極值。其中在生成函數(shù)類時需要曲線曲面適配器的指針，這里分別使用了由Handle管理的類和無Handle管理的類來對比，說明Handle的用法。即Handle是個智能指針，和C#中的內(nèi)存管理一樣，只需要new，不用手工delete。而沒用Handle管理的類，在new了之后，不再使用時，需要手工將內(nèi)存釋放。

生成BREP文件是為了便于在Draw Test Harness中查看顯示效果，計算結(jié)果顯示如下：

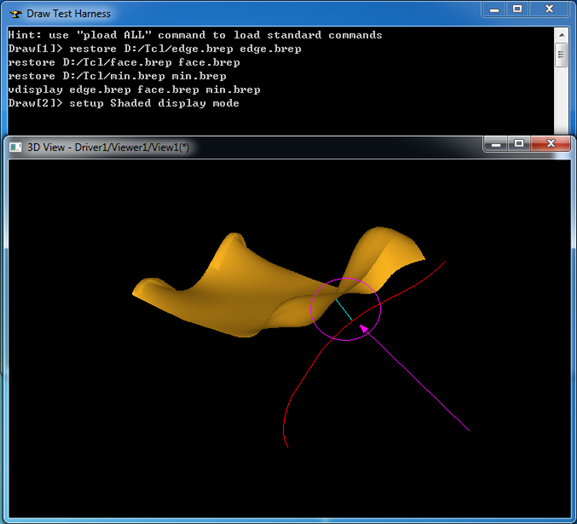
Figure 3.1 The minimum between a curve and a surface

如上圖所示的青色的線即是曲線和曲面之間距離最短的線。

4.Conclusion

綜上所述，在學(xué)習(xí)了最優(yōu)化理論之后，應(yīng)該結(jié)合實際進行應(yīng)用。從OPEN CASCADE的計算曲線和曲面之間的極值的類中可以學(xué)習(xí)如何將實際問題抽象成數(shù)學(xué)模型，進而使用數(shù)學(xué)工具對問題進行求解。

理解了多元函數(shù)的Newton法求極值，再回過頭去看看一元函數(shù)的求根或求極值問題，感覺應(yīng)該會簡單很多。如參數(shù)曲線曲面上根據(jù)三維點反求參數(shù)問題，就可以歸結(jié)為一元函數(shù)和二元函數(shù)的極值問題，可以很快寫出函數(shù)方程為如下：

同樣可以應(yīng)用Newton法來求極值。特別地，當(dāng)曲線和曲面有交點時，那么極值點就是曲線和曲面的交點了。

通過學(xué)習(xí)和應(yīng)用math_MultipleVarFunction及其子類，借鑒其將抽象數(shù)學(xué)概念用清晰的類來表示的方法，使程序便于理解，從而方便維護及擴展，提高程序質(zhì)量。例如，若從類math_MultipleVarFunctionWithHessian類派生，所以要求函數(shù)至少具有C2連續(xù)，才能使用Newton方法。

5. References

1. http://mathworld.wolfram.com/NewtonsMethod.html

2. https://en.wikipedia.org/wiki/Newton%27s_method_in_optimization

3. Shing Liu. OpenCASCADE Root-Finding Algorithm

4. http://tutorial.math.lamar.edu/Classes/CalcI/NewtonsMethod.aspx

5. 同濟大學(xué)數(shù)學(xué)教研室. 高等數(shù)學(xué). 高等教育出版社. 1996

6. 同濟大學(xué)應(yīng)用數(shù)學(xué)系. 線性代數(shù). 高等教育出版社. 2003

7. 易大義, 陳道琦. 數(shù)值分析引論. 浙江大學(xué)出版社. 1998

8. 《運籌學(xué)》教材編寫組. 運籌學(xué). 清華大學(xué)出版社. 2012

9. 何堅勇. 最優(yōu)化方法. 清華大學(xué)出版社. 2007

10. 楊慶之. 最優(yōu)化方法. 科學(xué)出版社. 2015

11. 王宜舉, 修乃華. 非線性最優(yōu)化理論與方法. 科學(xué)出版社. 2012

12. 趙罡, 穆國旺, 王拉柱. 非均勻有理B樣條. 清華大學(xué)出版社. 2010

PDF Version and Source Code Apply Newton Method to Find Extrema in OPEN CASCADE

只有注冊用戶登錄后才能發(fā)表評論。
【推薦】100%開源！大型工業(yè)跨平臺軟件C++源碼提供，建模，組態(tài)！

相關(guān)文章: OpenCASCADE HLR 輪廓線 OpenCASCADE-HLR Edge OpenCASCADE 線面求交 OpenCASCADE二維曲線求交 OpenCASCADE曲線上點的反求 OpenCASCADE - 曲線自交 OpenCASCADE 曲線求交 [書]-OpenCASCADE參考書籍 OpenCASCADE 掃掠曲面布爾數(shù)據(jù) 面的相交

網(wǎng)站導(dǎo)航: 博客園 IT新聞 BlogJava 博問 Chat2DB 管理

eryar

導(dǎo)航

公告

常用鏈接

留言簿(110)

隨筆分類(692)

隨筆檔案(603)

Links

搜索

最新評論

閱讀排行榜

評論排行榜

Apply Newton Method to Find Extrema in OPEN CASCADE

Apply Newton Method to Find Extrema in OPEN CASCADE