eryar

OpenCASCADE Root-Finding Algorithm

eryar@163.com

Abstract. A root-finding algorithm is a numerical method, or algorithm, for finding a value x such that f(x)=0, for a given function f. Such an x is called a root of the function f. In OpenCASCADE math package, implemente Newton-Raphson method to find the root for a function. The algorithm can be used for finding the extrema value for curve or surface, .i.e Point Inversion, find the parameter for a point on the curve or surface. The paper focus on the usage of OpenCASCADE method and its application.

Key Words. OpenCASCADE, Extrema, Newton-Raphson, Root-Finding, FunctionRoot

1. Introduction

代數方程求根問題是一個古老的數學問題，早在16世紀就找到了三次、四次方程的求根公式。但直到19世紀才證明n>=5次的一般代數方程式不能用代數公式求解。在工程和科學技術中，許多問題常常歸結為求解非線性方程的問題，因此，需要研究用數值方法求得滿足一定精度的代數方程式的近似解。

我國古代宋朝數學家秦九韶在他1247年所著的《數書九章》中，給出一個求代數方程根的近似方法，這個方法一般書上都稱為和納Horner方法（英國數學家W.G.Horner）。實際上Horner在1819年才提出這個方法，比秦九韶晚五百多年。每當看到教科書中這樣的介紹不知是該驕傲，還是該嗤之以鼻。古人發明創造的東西比外國人早，而現在國內用于CAD、CAM的軟件大都是國外進口的，像CATIA，AutoCAD，Pro/E，UG NX，SolidWorks，AVEVA Plant/Marine，Intergraph，ACIS，Parasolid……等等不勝枚舉，很少看到中國軟件的身影。而這些軟件廣泛應用于航空、造船、機械設計制造、工廠設計等各個行業，每年的軟件授權費用不知幾何？衷心希望當代國人奮發作為，為世界增添色彩。

閑話少說，本文主要關注非線性方程的數值解法，重點介紹了Newton-Rophson法及在OpenCASCADE中應用，即求點到曲線曲面的極值，也就是曲線曲面點的反求參數問題。對數值算法感興趣的讀者，可以參考《數值分析》、《計算方法》之類的書籍以獲取更詳細信息。

2.Numerical Methods

方程求根的方法有很多，在《數學手冊》中列舉了如下一些方法：

v 秦九韶法；

v 二分法；

v 迭代法；

v 牛頓法Newton’s Method；

v 弦截法；

v 拋物線法；

v 林士諤－趙訪熊法；

其中二分法是求實根的近似計算中行之有效的最簡單的方法，它只要求函數是連續的，因此它的使用范圍很廣，并便于在計算機上實現，但是它不能求重根也不能求虛根，且收斂較慢。

Newton法在單根鄰近收斂快，具有二階收斂速度，但Newton法對初值要求比較苛刻，即要求初值選取充分靠近方程的根，否則Newton法可能不收斂。擴大初值的選取范圍，可采用Newton下山法。

Newton’s Method的實現原理的演示動畫如下圖所示：

http://upload.wikimedia.org/wikipedia/commons/e/e0/NewtonIteration_Ani.gif

Figure 2.1 Newton’s Method(Newton-Raphson) 

由上面的動畫可以清楚理解Newton法的原理。用數學的文字描述如下：設f(x)二次連續可導，xk是f(x)=0的第k次近似解。我們用曲線y=f(x)過點(xk,yk)的切線Lk：

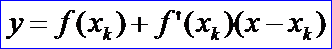
來近似曲線f(x)。取Lk與X軸的交點為f(x)=0的第k+1次近似解為：

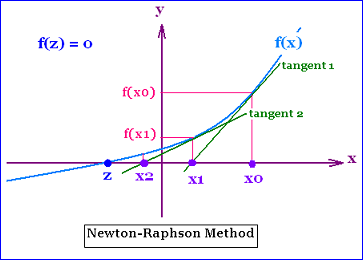
Figure 3.2 Newton-Raphson Method

其中：

稱為Newton公式。

Newton法對初值x0要求苛刻，在實際應用中往往難以滿足。Newton下山法是一種降低對初值要求的修正Newton法。

關于Newton方法的公開課的視頻我找到網易上有節課，介紹了Newton方法的原理及用法，網址為：http://v.163.com/movie/2006/8/T/V/M6GLI5A07_M6GLLGSTV.html，在后半部分。老師用實際例子來講解還挺有意思的，感興趣的讀者也可以完整地看看，也可復習下微積分的知識點。

3.OpenCASCADE Function Root

OpenCASCADE的math包中實現了方程求根的算法，相關的類有math_FunctionRoot，math_FunctionRoots，math_NewtonFunctionRoot等。在《Fundation Classes User’s Guide》中有對通用數學算法的介紹，即OpenCASCADE中實現了常見的數學算法：

v 求解線性代數方程的根的算法；

v 查找方程極小值的算法；

v 查找非線性方程（組）的根；

v 查找對角矩陣的特征值及特征向量的算法；

所有的數學算法以相同的方式來實現，即：在構造函數中來做大部分的計算，從而給出適當的參數。所有相關數據都保存到結果對象中，因此所有的計算盡量以最高效的方式來求解。函數IsDone()表明計算成功。如下所示分別為采用不同的算法來計算如下方程在[0，2]區間上的根：

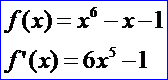
實現程序代碼如下所示：

由上述代碼可知，要想使用求根算法，必須從math_FunctionWithDerivative派生且重載其三個純虛函數Value(), Derivative(), Values()，在這三個純虛函數中計算相關的值及導數值即可。所以實際使用時，正確重載這三個函數是正確使用求根算法的關鍵。

求根用了三個不同的類，即三種方法來實現：

v math_FunctionRoot：即Newton-Raphson法；

v math_BissecNewton：是Newton-Raphson和二分法的組合算法；

v math_NewtonFunctionRoot：Newton Method；

計算結果如下圖所示：

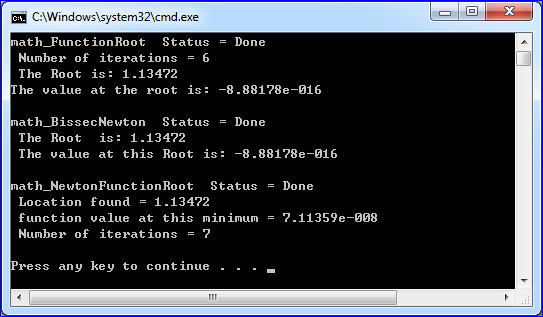
Figure 3.1 Root-Finding result of OpenCASCADE

由計算結果可知，三種方法計算的結果相同，都是1.13472，與書中結果吻合。但是math_NewtonFunctionRoot的迭代次比math_FunctionRoot多一次，且計算精度要低很多。

使用math_BissecNewton求根不用設置初始值，比較方便，精度與math_FunctionRoot一致。

4.Application

在工程和科學技術中，許多問題常常歸結為求解非線性方程的問題。在OpenCASCADE中的應用更多了，從下面一張類圖可見一斑：

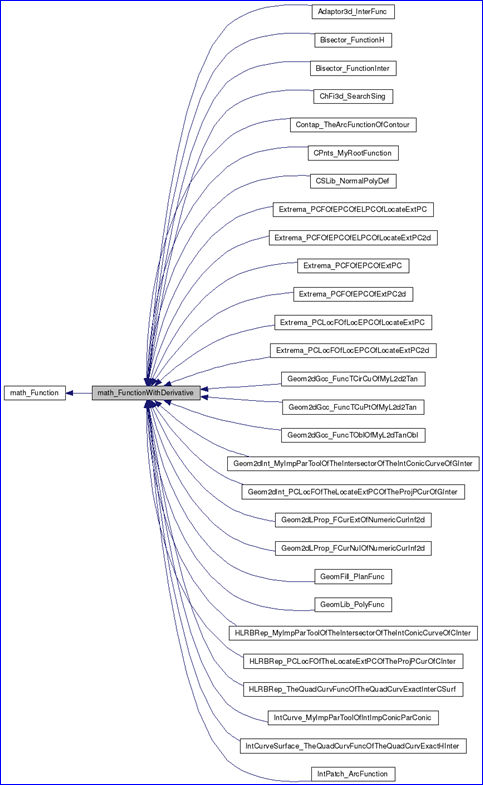
Figure 4.1 math_FunctionWithDerivative class diagram

由圖可知，從類math_FunctionWithDerivative派生出了很多可導函數的類，這些函數都可用于求根的類中，從而計算出對應方程的根。

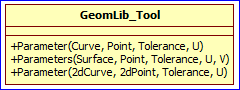
下面給出一個實際應用，即曲線曲面上點的反求問題，來說明如何應用上述求根算法來解決實際的問題。由于曲線曲面的參數表示法，通過參數u或(u,v)可以方便地求出曲線上的點或曲面上的點。若給定一個點P(x,y,z)，假設它在p次NURBS曲線C(u)上，求對應的參數u’使得C(u’)=P，這個問題稱為點的反求（point inverse）。在OpenCASCADE中提供了簡單的函數接口來實現點的反求，使用類為GeomLib_Tool：

如何將點的反求問題歸結為方程求根的問題，就要根據條件來建立方程了。一種簡單并完全可以解決這一問題的方法是：利用Newton迭代法來最小化點P和C(u)的距離，如下圖所示。如果最小距離小于一個事先指定的精度值，則認為點P在曲線上。這種方法有效地解決了更一般的“點在曲線上的投影”的問題。

因為方程求根的Newton方法需要指定初值u0，所以可按如下方法得到一個用于Newton法的初值u0：

v 如果已知點P在給定精度內位于曲線上，則用強凸包性確定候選的段，對于一般的點到曲線的投影問題，則選擇所要的段作為候選段；

v 在每個候選段上，計算n個按參數等間隔分布的點。計算出所有這些點和點P的距離，選擇其中距點P最近的點的參數作為u0。點數n一般利用某種啟發的方法來選擇。

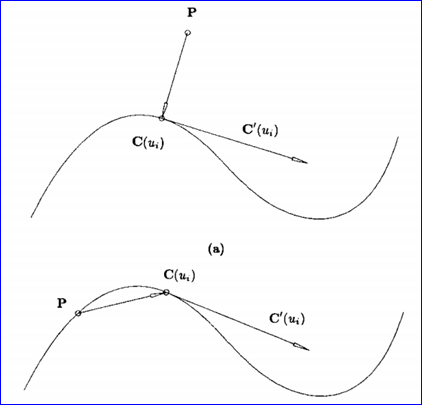
Figure 4.2 Point projection and Point inversion

需要強調的是使用Newton方法，一個好的初值對于迭代的收斂性及收斂速度是非常重要的。現在假設已經確定了初值u0，利用數量積定義函數：

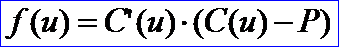
不管P點是否位于曲線上，當f(u)=0時，點P到C(u)的距離達到最小。對f(u)求導得：

代入Newton迭代公式得：

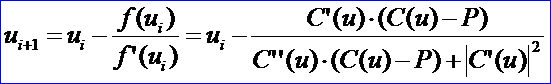
在OpenCASCADE中曲線點的反求主要是使用了派生自math_FunctionWithDerivative的類Extrema_PCFOfEPCOfExtPC，類圖如下所示：

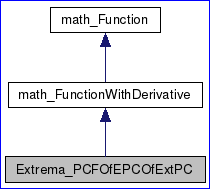
Figure 4.3 class diagram for point inverstion

所以需要實現三個純虛函數Value(), Derivative(), Values()，將其實現代碼列出如下所示：

根據代碼可知，實現原理與上述一致。下面給出一個簡單的例子，來說明及方便調試點的反求算法。示例程序代碼如下所示：

根據圓上一點，求出對應的參數值，計算結果如下所示：

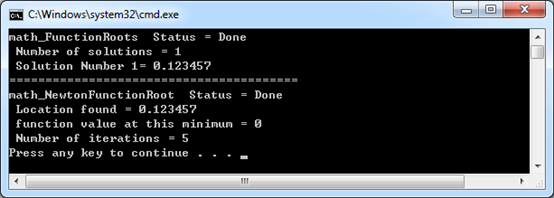
5.Conclusion

Newton法可以選作對導數能有效求值，且導數在根的鄰域中連續的任何函數方程的求根方法。Newton法在單根鄰近收斂快，精度高，具有二階收斂速度，但Newton法對初值要求比較高，即要求初值選取充分靠近方程的根，否則Newton法可能不收斂。

OpenCASCADE的math包中提供了求根的幾種實現算法，雖然代碼有些亂，但是這種抽象的思想還是相當不錯的，便于擴展應用。理解了math_FunctionRoot的算法，進而可以理解從math_FunctionWithDerivative派生的類的原理了。

通過曲線上點的反求問題引出使用求根算法的具體實例，從中可以看出關鍵還是要將實際問題抽象成一個方程。有了方程，根據Newton迭代公式，求出相應的值和導數值，就可以得到方程的高精度的根了。

對數值算法感興趣的讀者，可以參考《計算方法》、《數值分析》等相關書籍，從而可以在理解OpenCASCADE的代碼的基礎上，可以自己來實現相關算法。

6. References

1. 數學手冊編寫組. 數學手冊. 高等教育出版社. 1979

2. 趙罡，穆國旺，王拉柱譯. 非均勻有理B樣條. 清華大學出版社. 2010

3. Les Piegl, Wayne Tiller. The NURBS Book. Springer-Verlag. 1997

4. 易大義，沈云寶，李有法編. 計算方法. 浙江大學出版社. 2002

5. 易大義，陳道琦編. 數值分析引論. 浙江大學出版社. 1998

6. 李慶楊，王能超，易大義.數值分析.華中理工大學出版社. 1986

7. 同濟大學數學教研室. 高等數學(第四版). 高等教育出版社. 1996

8. Newton's Method video: 

http://v.163.com/movie/2006/8/T/V/M6GLI5A07_M6GLLGSTV.html

9. http://en.wikipedia.org/wiki/Root-finding_algorithm

10. http://mathworld.wolfram.com/Root-FindingAlgorithm.html

11. http://mathworld.wolfram.com/NewtonsMethod.html