OPEN CASCADE Multiple Variable Function
eryar@163.com
Abstract. Multiple variable function with gradient and Hessian matrix is very very import in OPEN CASCADE optimization algorithms. In order to understand these optimization algorithm better, let’s study some basic knowledge about Gradient, Hessian Matrix.
Key Words. Multiple Variable Function, Gradient, Hessian Matrix, 最優化算法,
1. Introduction
當函數只有一個自變量時，感覺相對簡單，一切還在掌握之中。如參數u表示的B樣條曲線，當參數u在[0，1]之間變化時，就可以得到與參數對應的曲線上的點。當函數有多個自變量時，就有點力不從心，畢竟人們都喜歡安穩，不喜歡太多的變化。當變化太多時，得到的結果也更豐富多彩。如有兩個參數u，v表示的B樣條曲面，參數變化的范圍是一個u∈[0，1]，v∈[0，1]矩形空間，與參數u，v對應的是一片曲面上的點。
在實際應用中，與多元函數的一階導數（Gradient梯度）、二階導數（Hessian Matrix）和多元函數的極值等概念也是理解非線性最優化問題的基礎知識。
OPEN CASCADE中一些求極值和逼近等算法中就使用了非線性最優化算法，如下類圖所示：
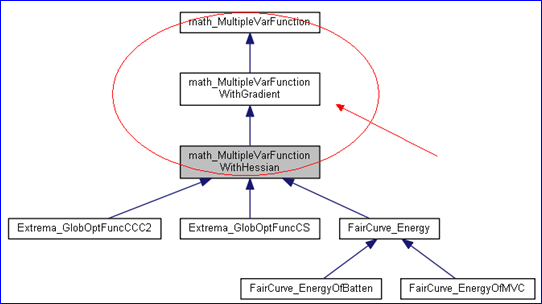
Figure 1.1 Multiple Variable Function in OPEN CASCADE
如上圖所示，具有二階導數（Hessian Matrix）的多元函數應用到全局優化的求極值算法中。在用能量法實現的曲線光順（Fair Curve）算法中也使用到了具有二階導數的多元函數。為了更好地理解最優化的具體實現，先學習下OPEN CASCADE中與多元函數有關概念的表達方式：多元函數、梯度Gradient和Hessian Matrix。
2.Multiple Variable Function
在《高等數學》中給出了多元函數的定義：設D是平面上一個點集。如果對于每個點P(x,y)∈D，變量z按照一定法則總有確定的值和它對應，則稱z是變量x,y的二元函數。點集D稱為該函數的定義域，x,y稱為自變量，z稱為因變量。當自變量的個數大于1個時，即n≥2，n元函數統稱為多元函數。
在OPEN CASCADE中與多元函數最直接的對應就是類Geom_Surface，即參數表示的曲面，參數u,v的取值區域為多元函數的定義域，當指定uv時得到的曲面上的點即為多元函數值。OPEN CASCADE的數學包中還給出了更抽象地多元函數類：math_MultipleVarFunction。
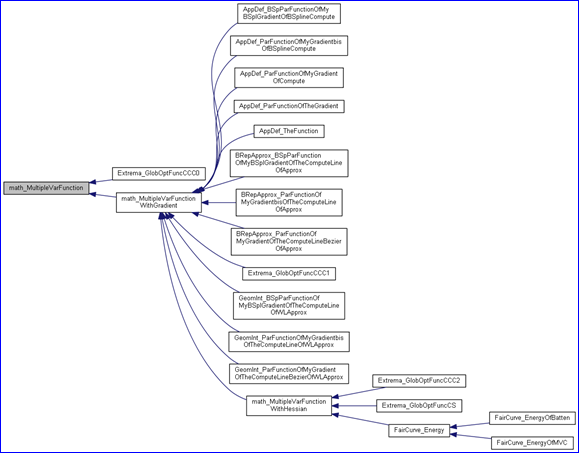
Figure 2.1 math_MultipleVarFunction class diagram
由上面的類圖可知，類math_MultipleVarFunction是個抽象類，有兩個純虛函數：
v NbVariables() const = 0：自變量的個數；
v Value(const math_Vector& X, Standard_Real& F) = 0：計算指定自變量X對應的函數值F。自變量X是個向量，其中的值分別對應多個自變量；
下面給出一個多元函數的具體應用，即計算二重積分。題目來源為《高等數學》教材習題9－2（1）：
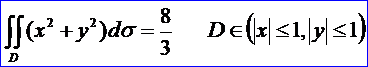
在OPEN CASCADE中計算上述二重積分代碼如下所示：
/*
* Copyright (c) 2015 Shing Liu All Rights Reserved.
*
* File : main.cpp
* Author : Shing Liu(eryar@163.com)
* Date : 2015-11-28 21:00
* Version : OpenCASCADE6.9.0
*
* Description : Test Gauss Multiple integration.
*/
#define WNT
#include <math_MultipleVarFunction.hxx>
#include <math_GaussMultipleIntegration.hxx>
#pragma comment(lib, "TKernel.lib")
#pragma comment(lib, "TKMath.lib")
class math_TestFunction : public math_MultipleVarFunction
{
public:
virtual Standard_Integer NbVariables() const
{
return 2;
}
virtual Standard_Boolean Value(const math_Vector& X, Standard_Real& F)
{
F = X(1) * X(1) + X(2) * X(2);
return Standard_True;
}
};
void testMultipleIntegration(void)
{
math_Vector aLower(1, 2);
math_Vector aUpper(1, 2);
math_IntegerVector aOrder(1, 2, 10);
aLower(1) = -1.0;
aLower(2) = -1.0;
aUpper(1) = 1.0;
aUpper(2) = 1.0;
math_TestFunction aFunction;
math_GaussMultipleIntegration aIntegrator(aFunction, aLower, aUpper, aOrder);
if (aIntegrator.IsDone())
{
std::cout << aIntegrator;
}
}
int main(int argc, char* argv[])
{
testMultipleIntegration();
return 0;
}
通過從抽象類math_MultipleVarFunction派生出一個具體的多元函數類，在虛函數Value()計算指定向量X對應的函數值，通過函數NbVariables()確定自變量的個數。為什么可以對類math_Vector的對象用括號直接進行取值和賦值呢？因為在這個類中重載了括號運算符。計算結果如下圖所示：
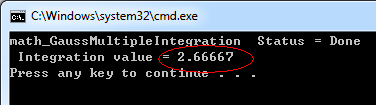
Figure 2.2 Integration Value
因為使用math_GaussMultipleIntegration時需要指定積分區域，且只能為常數，所以如下所示的積分區域中包含變量的多重積分就不能計算：
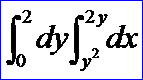
OPEN CASCADE中與多元函數對應的一元函數的積分計算參考：
OPEN CASCADE Gauss Integration:
http://www.shnenglu.com/eryar/archive/2014/09/11/208275.html
3.Gradient
在二元函數情形，設計函數z=f(x,y)在平面區域D內具有一階連續偏導數，則對于每一點P(x,y)∈D都可以定出一個向量：
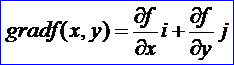
這向量稱為函數z=f(x,y)在點P(x,y)的梯度(gradient)，記作gradf(x,y)。對于多元函數u=f(X)，X=(x1,x2, ..., xn)T，有如下定義：
設u=f(X)，X∈S，若在點x0=(x1(0),x2(0), ..., xn(0))T處對于自變量X=(x1,x2, ..., xn)T的各個分量的偏導數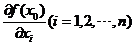
都存在，則稱函數u=f(X)在點x0處一階可導，并稱向量
是u=f(X)在點x0處的梯度Gradient或一階導數。
無約束優化最優性的一階必要條件是：若x0是無約束優化問題的局部最優值點，則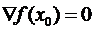
。
由數學分析可知，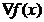
的方向為f(X)的等值面（等值線）的法線在點x0處的方向，即沿梯度方向函數值變化最快。目標函數梯度為零的點稱為無約束優化問題的穩定點。穩定點可能是目標函數的極大值點，也可能是極小值點，甚至二者都不是。最后一種情況對應的點稱為函數的鞍點，即在從該點出發的一個方向上是函數的極大值，而在另一個方向上是極小值點。
對無約束優化問題，目標函數在最優值點的任意方向上的導數都為零，即目標函數在最優值點的切平面是水平的。不過無約束優化問題的局部最大值點和鞍點也滿足上述條件。因此，要確認一個穩定點是否為最優值點，還需要考慮該點的二階最優性條件。
在OPEN CASCADE中與此對應的類是math_MultipleVarFunctionWithGradient，即具有梯度的多元函數。這個類也是抽象類，不能直接實例化，若要使用需要派生出新類，并實現以下幾個純虛函數：
v NbVariables() const = 0：多元函數自變量個數；
v Value(const math_Vector& X, Standard_Real& F) = 0：計算多元函數在指定變量X處對應的函數值F，通過引用傳出；
v Gradient(const math_Vector& X, math_Vector& G) = 0：計算多元函數在指定變量X處的梯度值，通過引用傳出；
v Values(const math_Vector& X, Standard_Real& F, math_Vector& G) = 0：計算多元函數在指定變量X處的函數值F和梯度值G；
4.Hessian Matrix
多元函數的二階導數和Hessian Matrix的定義如下：設u=f(X)，x0∈S，若f在點x0∈S處對于自變量x∈S的各分量的二階偏導數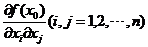
都存在，則稱函數f(X)在點x0處二階可導，且稱矩陣
為f(X)在點x0處的二階導數或Hessian Matrix，Hessian Matrix有時也記作H(x0)。
無約束最優化最優性條件的二階必要條件為：設f(X)在點x0∈S處二次可微，若x0最f(X)的局部極小點，則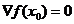
且
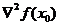半正定。
無約束最優化最優性條件的二階充分條件為：設f(X)在點x0∈S處二次可微，若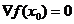
且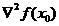
正定，則x0是函數f(X)的嚴格局部極小點。
二次型是X=(x1,x2,...,xn)T的二次齊次函數，它在研究非線性最優化問題中具有重要作用。通過線性代數中正定二次型相關定理，可以得出Hessian Matrix正定的判斷條件。相對于高等數學中關于二元函數極值充分條件的定理，使用Hessian Matrix更具一般性，適用于任意多元函數。終于知道正定二次型的一個應用，將原來在線性代數課本中突然冒出這么個抽象概念，能與實際應用有些關聯。看來線性代數必需在實際應用中才能有所理解，如關于現代控制工程中的微分方程組的求解，會用到特征值的理論；無約束最優化問題中極值充分條件的說明要用到正定二次型理論等。難怪當時在學習線性代數的時候那么吃力，對這些抽象概念不理解，學習的時候就只能是機械的記憶，如果以后用不到，肯定都還給老師了。OPEN CASCADE中與Hessian Matrix對應的類是math_MultipleVarFunctionWithHessian，其類圖如下所示：
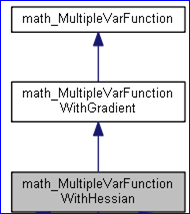
Figure 4.1 math_MultipleVarFunctionWithHessian class diagram
由上面類圖可知，math_MultipleVarFunctionWithHessian派生自帶梯度的多元函數類math_MultipleVarFunctionWithGradient。因此，比帶梯度的多元函數類多個求值的虛線函數：
Values(const math_Vector&X, Standard_Real&F, math_Vector&G, math_Matrix&H) = 0
通過這個線虛函數計算出多元函數在指定變量X處的函數F，梯度值G和Hessian Matrix H。
因為math_MultipleVarFunctionWithHessian有純虛函數，所以也不能直接實例化，需要根據實際情況從其派生類來使用。正如本文開頭所示的類圖中幾個類一樣，從帶有Hessian Matrix的多元函數派生出新類來計算全局極值和曲線光順，如下類圖所示：
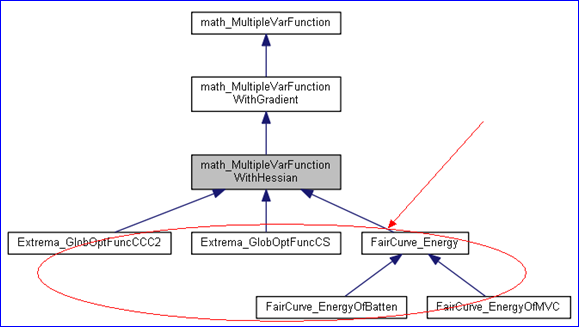
Figure 4.2 math_MultipleVarFunctionWithHessian class diagram
5.Conclusion
在OPEN CASCADE的數學包Package math中不僅描述了只有一個自變量的一元函數math_Function，也描述了具有多個自變量的多元函數，及其一階導數（梯度）和二階導數（Hessian Matrix）。通過應用多元函數的積分計算，可以看出OCC對這些概念進行的類封裝還是很清晰，便于理解和使用。對于這些基礎概念的介紹，便于理解后面具體的優化算法的使用。
從OPEN CASCADE中的優化算法可以看出，核心是數學這個精巧工具的熟練應用。可以找出《高等數學》、《線性代數》、《最優化方法》、《非線性最優化理論與方法》、《數值分析》等相關書籍，通過對比OPEN CASCADE中的程序實現有效的理論聯系實踐，提高學習效率。而對高等數學和線性代數可以做到溫故知新，對原來百思不解的問題可以有個Aha!的恍然大悟，找到學習的樂趣。
6. References
1. 同濟大學數學教研室. 高等數學. 高等教育出版社. 1996
2. 同濟大學應用數學系. 線性代數. 高等教育出版社. 2003
3. 易大義, 陳道琦. 數值分析引論. 浙江大學出版社. 1998
4. 《運籌學》教材編寫組. 運籌學. 清華大學出版社. 2012
5. 何堅勇. 最優化方法. 清華大學出版社. 2007
6. 楊慶之. 最優化方法. 科學出版社. 2015
7. 王宜舉, 修乃華. 非線性最優化理論與方法. 科學出版社. 2012