OpenCASCADE Gauss Integration
eryar@163.com
Abstract. Numerical integration is the approximate computation of an integral using numerical techniques. The numerical computation of an integral is sometimes called quadrature. The most straightforward numerical integration technique uses the Newton-Cotes formulas(also called quadrature formulas), which approximate a function tabulated sequence of regularly spaced intervals by various degree polynomials. If the functions are known analytically instead of being tabulated at equally spaced intervals, the best numerical method of integrations is called Gauss Integration(Gaussian quadrature). By picking the abscissas at which to evaluate the function, Gaussian quadrature produces the most accurate approximations possible. In OpenCASCADE math package it implement the Gauss-Legendre integration. So I will focus on the usage of the class in OpenCASCADE.
Key Words. OpenCASCADE, Gauss Integration, Gauss-Legendre, Numerical Analysis
1. Introduction
在科學和工程計算問題中,經常要計算一些定積分或微分,它們的精確值無法算出或計算量太大,只能用數值的方法給出具有指定誤差限的近似值。最直觀的數值積分方法有Newton-Cotes,其將積分區間等分之,并取分點為積分節點。這種做法雖然簡化了計算,但卻降低了所得公式的代數精度。
Gauss型求積公式是一種高精度的數值積分公式。在求積節點數相同的情況下,即計算工作量相近的情況下,利用Gauss型求積公式往往可以獲得準確程序較高的積分結果,只是它在不等距的無理數上計算被積函數。
OpenCASCADE的math包中實現了Gauss-Legendre積分算法。本文主要介紹其使用方法,進而對其應用進行理解。
2. The Gauss-Legendre Integration
Gauss型求積公式是數值穩定的,且對有限閉區間上的連續函數,Gauss求積的數值隨節點數目的增加而收斂到準確積分值。
常用的Gauss型求積公式有Gauss-Legendre求積公式,Gauss-Chebyshev求積公式,Gauss-Laguerre求積公式和Gauss-Hermite求積公式等。
對于一般區間[a, b]上的Gauss型求積公式,可通過變量變換,由Gauss-Legendre求積公式得到:
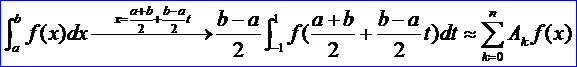 其中:
其中:
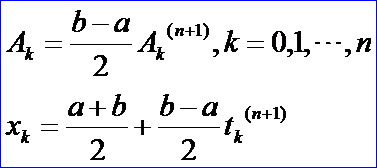
OpenCASCADE中對應的類有math_GaussSingleIntegration,主要實現的函數為Perform(),計算過程如下:
v 查表求得Gauss點及求積系數;
//Recuperation des points de Gauss dans le fichier GaussPoints.
math::GaussPoints(Order,GaussP);
math::GaussWeights(Order,GaussW);
v 根據Gauss-Legendre求積公式計算;
// Changement de variable pour la mise a l'echelle [Lower, Upper] :
xm = 0.5*(Upper + Lower);
xr = 0.5*(Upper - Lower);
Val = 0.;
Standard_Integer ind = Order/2, ind1 = (Order+1)/2;
if(ind1 > ind) { // odder case
Ok1 = F.Value(xm, Val);
if (!Ok1) return;
Val *= GaussW(ind1);
}
// Sommation sur tous les points de Gauss: avec utilisation de la symetrie.
for (j = 1; j <= ind; j++) {
dx = xr*GaussP(j);
Ok1 = F.Value(xm-dx, F1);
if(!Ok1) return;
Ok1 = F.Value(xm+dx, F2);
if(!Ok1) return;
// Multiplication par les poids de Gauss.
Standard_Real FT = F1+F2;
Val += GaussW(j)*FT;
}
// Mise a l'echelle de l'intervalle [Lower, Upper]
Val *= xr;
對比Gauss-Legendre求積公式來理解上述代碼還是比較清晰的。下面給出使用此類的一個具體實例:
/*
* Copyright (c) 2014 eryar All Rights Reserved.
*
* File : Main.cpp
* Author : eryar@163.com
* Date : 2014-09-11 20:46
* Version : 1.0v
*
* Description : Demo for Gauss-Legendre Integration usage.
*
* Key words : OpenCascade, Gauss-Legendre Integration
*/
#define WNT
#include <math_Function.hxx>
#include <math_GaussSingleIntegration.hxx>
#pragma comment(lib, "TKernel.lib")
#pragma comment(lib, "TKMath.lib")
class Test_GaussFunction : public math_Function
{
public:
virtual Standard_Boolean Value(const Standard_Real x, Standard_Real &y)
{
y = x;
return Standard_True;
}
private:
};
void TestGaussIntegration(void)
{
Test_GaussFunction aFunction;
math_GaussSingleIntegration aSolver(aFunction, 1, 10, 10);
std::cout << aSolver << std::endl;
}
int main(int argc, char* argv[])
{
TestGaussIntegration();
return 0;
}
主要是從math_Function派生一個類來在虛函數Value()中重定義求積函數即可。上述實例中計算的是如下積分:
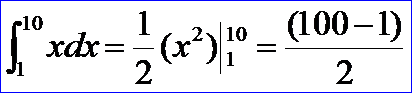
計算結果如下圖所示:
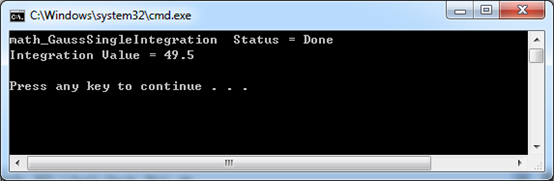
Figure 2.1 Gauss-Legendre Integtation Result
3. Application
由高等數學知識可知,積分的應用主要用于計算圖形面積,體積及曲線的弧長,功等。
積分在OpenCASCADE中的主要應用有計算曲線長度,曲面面積及實體的體積等。如下圖所示:
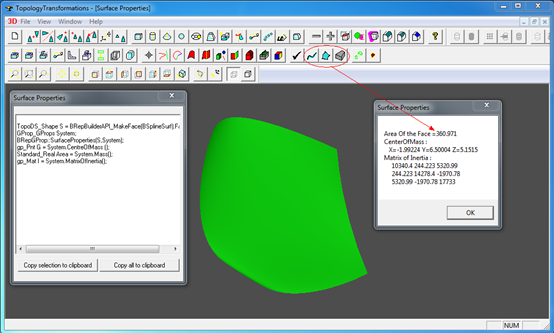
Figure 3.1 Compute Area of a Surface
示例代碼如下所示:
TopoDS_Shape S = BRepBuilderAPI_MakeFace(BSS, Precision::Confusion()).Face();
GProp_GProps System;
BRepGProp::SurfaceProperties(S,System);
gp_Pnt G = System.CentreOfMass ();
Standard_Real Area = System.Mass();
gp_Mat I = System.MatrixOfInertia();
4. Conclusion
OpenCASCADE中實現的Gauss-Legendre求積算法,由于是查表求得Gauss點及求積系數,所以計算速度快。唯一不足是對高斯點數有限制。
綜上所述,可知數值計算在OpenCASCADE中重要作用。一個TKMath庫相當于實現了一本《數值分析》課本中的大部分內容。所以有興趣的朋友可結合《數值分析》或《計算方法》之類的書籍,來對OpenCASCADE的數學庫TKMath進行理論聯系實際的深入理解。
5. References
1. Wolfram MathWorld, Numerical Integration,
http://mathworld.wolfram.com/NumericalIntegration.html
2. 易大義,沈云寶,李有法編. 計算方法. 浙江大學出版社. 2002
3. 易大義,陳道琦編. 數值分析引論. 浙江大學出版社. 1998
4. 李慶楊,王能超,易大義.數值分析.華中理工大學出版社. 1986
5. 同濟大學數學教研室. 高等數學(第四版). 高等教育出版社. 1996