OpenCASCADE Interpolation - Lagrange
eryar@163.com
Abstract. Power basis polynomial is the most simple polynomial function. It also be called power series. OpenCASCADE provides basic computation functions for polynomial functions, such as evaluate the result for a given polynomial, Lagrange interpolation, Hermite interpolation, .etc. The package named PLib, means Polynomial functions Library. The paper focus on the Lagrange interpolation usage of PLib.
Key Words. OpenCASCADE, PLib, Interpolation, Lagrange, 插值
1.Introduction
無(wú)窮級(jí)數(shù)是高等數(shù)學(xué)的一個(gè)重要組成部分，它是表示函數(shù)、研究函數(shù)性質(zhì)及進(jìn)行數(shù)值計(jì)算的一種工具。由高等數(shù)學(xué)中的無(wú)窮級(jí)數(shù)的概念可知，函數(shù)項(xiàng)級(jí)數(shù)中簡(jiǎn)單而常見(jiàn)的一類(lèi)級(jí)數(shù)就是各項(xiàng)都是冪函數(shù)的函數(shù)項(xiàng)級(jí)數(shù)即所謂的冪級(jí)數(shù)（Power Series）。因?yàn)閮缂?jí)數(shù)的形式簡(jiǎn)單，易于理解，且可以高效計(jì)算曲線(xiàn)上的點(diǎn)及各階導(dǎo)數(shù)，所以在幾何造型中經(jīng)常用冪級(jí)數(shù)來(lái)近似表示曲線(xiàn)曲面。由于將函數(shù)展開(kāi)成冪級(jí)數(shù)是有條件的，所有并不是所有的曲線(xiàn)曲面都可以用冪級(jí)數(shù)的多項(xiàng)式來(lái)逼近。
對(duì)無(wú)窮級(jí)數(shù)概念比較陌生的讀者可以把《高等數(shù)學(xué)》的書(shū)找出來(lái)翻翻看，重溫一下大學(xué)的時(shí)光。一打開(kāi)做了筆記有點(diǎn)泛黃的舊書(shū)，就會(huì)回想起青澀的校園時(shí)光。
當(dāng)時(shí)學(xué)習(xí)《高等數(shù)學(xué)》的時(shí)候感覺(jué)很抽象難理解，因?yàn)闊o(wú)法將理論與實(shí)踐聯(lián)系起來(lái)，看不到直觀效果，有時(shí)也會(huì)冒出“學(xué)數(shù)學(xué)有什么用？”這種問(wèn)題。當(dāng)你遇到相關(guān)的問(wèn)題再去看國(guó)內(nèi)的教材時(shí)，覺(jué)得國(guó)內(nèi)的教材寫(xiě)得還是很細(xì)致用心的。現(xiàn)在獲取信息已經(jīng)很便利了，如OpenCASCADE這個(gè)開(kāi)源的庫(kù)，其TKMath工具箱可以看成是數(shù)值計(jì)算理論聯(lián)系實(shí)踐的一個(gè)具體實(shí)例。結(jié)合OpenCASCADE的源碼來(lái)對(duì)相關(guān)理論的學(xué)習(xí)，效率會(huì)事半功倍。
本文對(duì)冪級(jí)數(shù)的概念做簡(jiǎn)單介紹，并結(jié)合源程序詳細(xì)說(shuō)明OpenCASCADE中的PLib包中關(guān)于冪級(jí)數(shù)多項(xiàng)式的計(jì)算及Lagrange插值的用法。
2.Polynomial Evaluation
高等數(shù)學(xué)的書(shū)中把冪級(jí)數(shù)的重點(diǎn)落在如何將其他的函數(shù)展開(kāi)成冪級(jí)數(shù)，即用冪級(jí)數(shù)來(lái)逼近函數(shù)，而沒(méi)有介紹如何用數(shù)值的方法來(lái)對(duì)冪級(jí)數(shù)進(jìn)行計(jì)算。在算法導(dǎo)論一書(shū)[2]中找到相關(guān)多項(xiàng)式的表示及計(jì)算的實(shí)現(xiàn)方法，給出了多項(xiàng)式在數(shù)據(jù)結(jié)構(gòu)上的表示方式及求值算法。對(duì)于一個(gè)冪級(jí)數(shù)多項(xiàng)式：
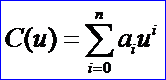
多項(xiàng)式的表示有系數(shù)表示法和點(diǎn)值表示法。系數(shù)表示法（Coefficient Representation）就是將多項(xiàng)式的系數(shù)組成一個(gè)向量來(lái)表示這個(gè)多項(xiàng)式。對(duì)用系數(shù)表示法表示的多項(xiàng)式的求值計(jì)算可以采用Horner法則，也是是著名的秦九韶算法。此算法的實(shí)現(xiàn)代碼在《The NURBS Book》[3]一書(shū)中給出了，此處略去，只給出OpenCASCADE中對(duì)冪級(jí)數(shù)多項(xiàng)式的計(jì)算的函數(shù)的使用。
void testPolynomialEvaluation(void)
{
// evaluate 1 dimension polynmoial.
Standard_Real aCoeff[3] = {2.0, 2.0, 3.0};
Standard_Real aResult = 0.0;
for (int i = 0; i < 3; ++i)
{
PLib::EvalPolynomial(i, 0, 2, 1, aCoeff[0], aResult);
std::cout << "x=" << i << ", (2.0 + 2.0*x + 3.0*x^2): " << aResult << std::endl;
}
}
從上述代碼可以看出，OpenCASCADE的PLib包中對(duì)多項(xiàng)式的表示方法是采用的系數(shù)表示法。其系數(shù)分別為：2.0，2.0，3.0，即表示了冪級(jí)數(shù)：
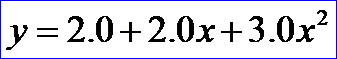
當(dāng)x=0, 1,2時(shí)計(jì)算結(jié)果如下圖所示：
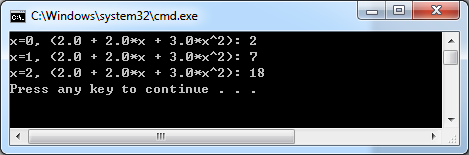
Figure 2.1 Polynomial Evaluation
3.Polynomial Interpolation
多項(xiàng)式的插值問(wèn)題是多項(xiàng)式求值的逆問(wèn)題。多項(xiàng)式求值問(wèn)題幾何意義就是已知曲線(xiàn)的表達(dá)式計(jì)算曲線(xiàn)上的點(diǎn)；而插值問(wèn)題是已經(jīng)曲線(xiàn)上的一些點(diǎn)來(lái)求通過(guò)這些點(diǎn)的曲線(xiàn)表達(dá)式。多項(xiàng)式插值中最常見(jiàn)最基本的問(wèn)題是求一次數(shù)不超過(guò)n的代數(shù)多項(xiàng)式：
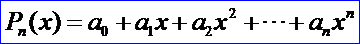
使
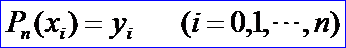
滿(mǎn)足插值條件的多項(xiàng)式稱(chēng)為函數(shù)f(x)在節(jié)點(diǎn)xi處的n次插值多項(xiàng)式。由插值條件可知，插值多項(xiàng)式的系數(shù)滿(mǎn)足線(xiàn)性方程組：
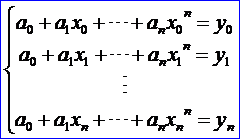
由線(xiàn)性代數(shù)可知，其系數(shù)行列式是n+1階Vandermonde行列式，且：
因?yàn)椴逯档狞c(diǎn)是不同的點(diǎn)，所以行列式V不為0，即線(xiàn)性方程組有唯一解。這也是算法導(dǎo)論一書(shū)中這樣說(shuō)“從某種意義上說(shuō)，多項(xiàng)式的系數(shù)表示法與點(diǎn)值表示法是等價(jià)的，即用點(diǎn)值形式表示的多項(xiàng)式都對(duì)應(yīng)唯一一個(gè)系數(shù)形式的多項(xiàng)式”的理論依據(jù)。即插值多項(xiàng)式的唯一性。這里不僅指出了插值多項(xiàng)式存在的唯性，而且也提供了一種解法，即通過(guò)解線(xiàn)性方程組來(lái)確定系數(shù)。根據(jù)這個(gè)思路，給出對(duì)上面已知系數(shù)求值的多項(xiàng)式進(jìn)行插值，代碼如下所示：
void testPolynomialInterpolation(void)
{
// given three points: (0, 2), (1, 7), (2, 18) to interpolate a polynomial
math_Matrix A(1, 3, 1, 3, 0.0);
math_Vector B(1, 3);
math_Vector X(1, 3);
A(1, 1) = 1.0; A(1, 2) = 0.0; A(1, 3) = 0.0; B(1) = 2.0;
A(2, 1) = 1.0; A(2, 2) = 1.0; A(2, 3) = 1.0; B(2) = 7.0;
A(3, 1) = 1.0; A(3, 2) = 2.0; A(3, 3) = 4.0; B(3) = 18.0;
// solve functions: Ax = B
math_Gauss aSolver(A);
aSolver.Solve(B, X);
if (aSolver.IsDone())
{
std::cout << X << std::endl;
}
}
已知多項(xiàng)式通過(guò)三個(gè)點(diǎn)（0, 2），（1, 7），（2, 18)，求通過(guò)這三個(gè)點(diǎn)的多項(xiàng)式表達(dá)式。根據(jù)插值條件列出線(xiàn)性方程組如下：
將系數(shù)a0,a1,a2看成線(xiàn)性方程組的待求變量，使用類(lèi)math_Gauss來(lái)對(duì)線(xiàn)性方程組進(jìn)行求解，計(jì)算結(jié)果如下所示：
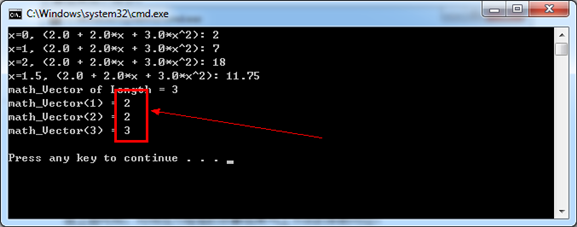
Figure 3.1 Polynomial Interpolation Result
由上圖可知，對(duì)線(xiàn)性方程組的求解結(jié)果與上節(jié)點(diǎn)的系數(shù)對(duì)應(yīng)。
4.Lagrange Interpolation
在《計(jì)算方法》、《數(shù)值逼近》等書(shū)中看到Lagrange的名字，就想到《高等數(shù)學(xué)》書(shū)中很多與之相關(guān)的定理、定義等，如：Lagrange中值定理、Lagrange型余項(xiàng)、條件極值的Lagrange乘數(shù)法等等。在網(wǎng)上搜索了下Lagrange，原來(lái)他也是OpenCASCADE的發(fā)源地的人：法國(guó)人。Joseph-Louis Lagrange，法國(guó)著名數(shù)學(xué)家、物理學(xué)家。1736年1月25日生于意大利都靈，1813年4月10日卒于法國(guó)巴黎。他在數(shù)學(xué)、力學(xué)和天文學(xué)三個(gè)學(xué)科領(lǐng)域都有歷史性的貢獻(xiàn)，其中尤以數(shù)學(xué)方面的成就最為突出。以下圖片來(lái)自網(wǎng)易公開(kāi)課《數(shù)學(xué)傳奇》：從笛卡爾到龐加萊—法國(guó)數(shù)學(xué)的人文傳統(tǒng)，公開(kāi)課網(wǎng)址：http://open.163.com/special/cuvocw/shuxuechuanqi.html
為什么優(yōu)雅浪漫的法國(guó)人的數(shù)學(xué)大師層出不窮呢？因?yàn)樗麄冏顑?yōu)秀的人在學(xué)習(xí)數(shù)學(xué)。數(shù)學(xué)已經(jīng)成為法國(guó)人傳統(tǒng)文化中最優(yōu)秀的一部分了。
數(shù)學(xué)也是中國(guó)傳統(tǒng)文化的一部分，中國(guó)古代數(shù)學(xué)成就也很多：《周髀算經(jīng)》； 《九章算術(shù)》（三國(guó)時(shí)劉徽著）； 祖沖之； 算盤(pán)。天文學(xué)：天象觀察記錄， 發(fā)明觀測(cè)儀器：圭表；渾儀；簡(jiǎn)儀；高表；仰儀，制定歷法(農(nóng)歷)。想想后來(lái)為什么沒(méi)有大的發(fā)展，原因可能是科舉制度造成的，考試的內(nèi)容偏文。
Lagrange父親是法國(guó)陸軍騎兵里的一名軍官，后由于經(jīng)商破產(chǎn)，家道中落。據(jù)Lagrange本人回憶，如果幼年時(shí)家境富裕，他也就不會(huì)作數(shù)學(xué)研究了。經(jīng)歷了挫折之后沒(méi)被打倒的人后期成就會(huì)更大，像《紅樓夢(mèng)》的作者曹雪芹。嚴(yán)重跑題了，回到Lagrange插值問(wèn)題上來(lái)。從Lagrange中值定理的證明及Lagrange乘數(shù)法求極值的方式中可以看出Lagrange有個(gè)特點(diǎn)，那就是喜歡引入輔助函數(shù)來(lái)解決問(wèn)題，可以看出Lagrange是非常精明的。對(duì)多項(xiàng)式插值也不例外，通過(guò)構(gòu)造了一個(gè)Lagrange插值基函數(shù)來(lái)簡(jiǎn)化多項(xiàng)式的插值，如下公式為L(zhǎng)agrange插值基函數(shù)：
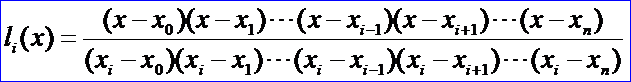設(shè)：
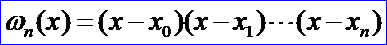
則Lagrange插值基函數(shù)可以表示為簡(jiǎn)潔的形式：
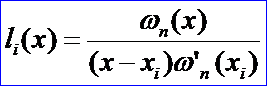
則n次多項(xiàng)式
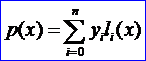
滿(mǎn)足插值條件。OpenCASCADE的PLib包中也提供了Lagrange插值的函數(shù)來(lái)進(jìn)行多項(xiàng)式插值計(jì)算。其用法的代碼如下所示：
void testLagrangeInterpolation(void)
{
// given three points: (0,2), (1,7), (2,18) to interpolate a polynomial
Standard_Real aValues[3] = {2.0, 7.0, 18.0};
Standard_Real aParameters[3] = {0.0, 1.0, 2.0};
Standard_Real aResult = 0.0;
// this do not output the coeff of the interpolate polynomial
PLib::EvalLagrange(1.5, 0, 2, 1, aValues[0], aParameters[0], aResult);
std::cout << "Result: " << aResult << std::endl;
}
下面對(duì)PLib::EvalLagrange()函數(shù)的7個(gè)參數(shù)進(jìn)行說(shuō)明：
Parameter | 待根據(jù)Lagrange插值多項(xiàng)式求值的參數(shù) |
DerivativeRequest | 插值多項(xiàng)式導(dǎo)數(shù)次數(shù) |
Degree | 插值多項(xiàng)式的次數(shù) |
Dimension | 插值多項(xiàng)式的維次 |
Values | 插值多項(xiàng)式的值 |
Parameters | 插值多項(xiàng)式的參數(shù) |
Results | 參數(shù)Parameter在Lagrange插值多項(xiàng)式中的值 |
上述代碼計(jì)算的是這樣一個(gè)問(wèn)題，已知f(0)=2; f(1)=7, f(2)=18，求f(1.5)的近似值。計(jì)算結(jié)果如下圖所示：
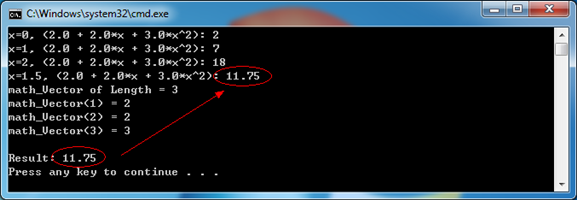
Figure 4.1 Lagrange Interpolation Result
由上圖可知，經(jīng)過(guò)Lagrange拋物插值得到的結(jié)果與直接計(jì)算得到的結(jié)果吻合。為了更好的說(shuō)明OpenCASCADE中PLib包的Lagrange插值的用意，下面將《計(jì)算方法》[6]中Lagrange插值部分中的例題進(jìn)行計(jì)算來(lái)結(jié)計(jì)算結(jié)果進(jìn)行比較。已知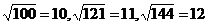
分別用線(xiàn)性插值和拋物插值求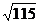
的近似值。相關(guān)計(jì)算代碼如下所示：
// sqrt(100)=10, sqrt(121)=11, sqrt(144)=12, evaluate sqrt(115) value.
Standard_Real aSqrtValues[3] = {10.0, 11.0, 12.0};
Standard_Real aSqrtParameters[3] = {100.0, 121.0, 144.0};
// linear interpolation
PLib::EvalLagrange(115.0, 0, 1, 1, aSqrtValues[0], aSqrtParameters[0], aResult);
std::cout << "Linear Interpolate Result: " << aResult << std::endl;
// Parabolic Interpolation
PLib::EvalLagrange(115.0, 0, 2, 1, aSqrtValues[0], aSqrtParameters[0], aResult);
std::cout << "Parabolic Interpolate Result: " << aResult << std::endl;
計(jì)算結(jié)果如下所示：
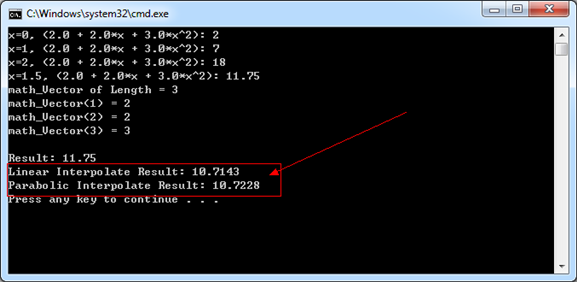
Figure 4.2 Linear Interpolate and Parabolic Interpolate Result
將上圖4.2的結(jié)果與書(shū)中的計(jì)算結(jié)果進(jìn)行對(duì)比發(fā)現(xiàn)，下面的結(jié)果為《計(jì)算方法》書(shū)中的結(jié)果：
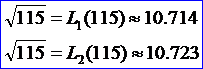
PLib中Lagrange插值結(jié)果準(zhǔn)確，精度較高。
從上面的結(jié)果來(lái)看，Lagrange插值方法比直接解線(xiàn)性方程組的方法要簡(jiǎn)單，且Lagrange插值法比解線(xiàn)性方程組的實(shí)現(xiàn)要簡(jiǎn)單很多，只用一個(gè)函數(shù)即可。
5.Conclusion
通過(guò)將最簡(jiǎn)單的多項(xiàng)式進(jìn)行求值，及用求解線(xiàn)性方程組的方法插值和Lagrange插值多項(xiàng)式，來(lái)學(xué)習(xí)曲線(xiàn)擬合中要求較高“插值”，因?yàn)槠湟笄€(xiàn)嚴(yán)格通過(guò)插值點(diǎn)。曲線(xiàn)擬合中的逼近就沒(méi)有這個(gè)要求，只是要求曲線(xiàn)與插值點(diǎn)之間的容差盡量小。
通過(guò)應(yīng)用OpenCASCADE的PLib包中的函數(shù)，可以發(fā)現(xiàn)對(duì)冪級(jí)數(shù)的多項(xiàng)式的表示法一般會(huì)用系數(shù)表示法，且都會(huì)使用高效的Horner法則，也是秦九韶算法。
直接根據(jù)定義來(lái)插值冪次多項(xiàng)式時(shí)，可以使用Gauss消元法來(lái)求解線(xiàn)性方程組。這種方式計(jì)算工作量大，而Lagrange插值法結(jié)構(gòu)緊湊，便于編程實(shí)現(xiàn)，且代碼相對(duì)簡(jiǎn)單。通過(guò)對(duì)《計(jì)算方法》書(shū)中例題的計(jì)算，來(lái)驗(yàn)證PLib::EvalLagrange()函數(shù)的用法及計(jì)算結(jié)果。
6.References
1. 同濟(jì)大學(xué)數(shù)學(xué)教研室. 高等數(shù)學(xué). 高等教育出版社. 1996
2. 同濟(jì)大學(xué)應(yīng)用數(shù)學(xué)系. 線(xiàn)性代數(shù). 高等教育出版社. 2003
3. Thomas H. Cormen. Introduction to Algorithms. The MIT Press. 2001
4. Les Piegl, Wayne Tiller. The NURBS Book. Springer-Verlag. 1995
5. Shing Liu. Polynomial Library in OpenCASCADE. 2013
http://www.shnenglu.com/eryar/archive/2013/05/08/200118.html
6. 易大義,沈云寶,李有法. 計(jì)算方法. 浙江大學(xué)出版社. 2002
7. 蔣爾雄,趙風(fēng)光,蘇仰鋒. 數(shù)值逼近. 復(fù)旦大學(xué)出版社. 2012
8. 王仁宏,李崇君,朱春鋼. 計(jì)算幾何教程. 科學(xué)出版社. 2008
9. 蔡天新. 數(shù)學(xué)傳奇. http://open.163.com/special/cuvocw/shuxuechuanqi.html
10. 科學(xué)出版社名詞室. 新漢英數(shù)學(xué)詞匯. 科學(xué)出版社. 2004