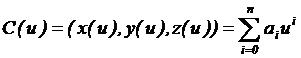Polynomial Library in OpenCascade
eryar@163.com
摘要Abstract：分析冪基曲線即多項式曲線在OpenCascade中的計算方法，以及利用OpenSceneGraph來顯示OpenCascade的計算結(jié)果，加深對多項式曲線的理解。
關(guān)鍵字Key Words：OpenCascade、PLib、OpenSceneGraph、Polynomial Library
一、 概述 Overview
CAGD（Computer Aided Geometry Design）中，基表示的參數(shù)矢函數(shù)形式已經(jīng)成為形狀數(shù)學描述的標準形式。人們首先注意到在各類函數(shù)中，多項式函數(shù)（Polynomial Function）能較好地滿足要求。它表示形式簡單，又無窮次可微，且容易計算函數(shù)值及各階導數(shù)值。采用多項式函數(shù)作為基函數(shù)即多項式基，相應(yīng)可以得到參數(shù)多項式曲線曲面。
人們很早就注意到這樣一個問題：設(shè)f(x)∈C[a,b]，對于任意給的ε>0，是否存在這樣的多項式p(x)，使得
對一切a≤x≤b一致成立？
1885年，Weierstrass證明了p(x)的存在性；
1912年，Bernstein將滿足條件的多項式構(gòu)造出來。
Weierstrass定理：設(shè)f(x)∈C[a,b]，那么對于任意給的ε>0，都存在這樣的多項式p(x)，使得
Weierstrass定理說明，[a,b]上的任何連續(xù)函數(shù)都可以用多項式來一致逼近。該定理實際上正好解決了利用多項式組成的函數(shù)來表示連續(xù)函數(shù)的問題。
冪（又稱單項式monomial）基uj(j=0,1,,,n)是最簡單的多項式基。相應(yīng)多項式的全體構(gòu)成n次多項式空間。n次多項式空間中任一組n+1個線性無關(guān)的多項式都可以作為一組基，因此就有無窮多組基。不同組基之間僅僅相差一個線性變換。
如果允許坐標函數(shù)x(u)，y(u)，z(u)是任意的，則可以得到范圍很廣的曲線。但是在實際開發(fā)一個幾何造型系統(tǒng)時，我們需要一些折中，理想的情況是將坐標函數(shù)限制在滿足下述條件的一類函數(shù)中：
l 能夠精確地表示用戶需要的所有曲線；
l 在計算機中能夠被方便、高效、精確地處理，特別是可以高效地計算曲線上的點及各階導矢；函數(shù)的數(shù)值計算對浮點數(shù)舍入誤差不敏感；函數(shù)所需要的存儲量較小；
l 比較簡單，在數(shù)學上易于理解。
一類被廣泛使用的函數(shù)就是多項式。盡管它們滿足上標準中的后兩項，但有很多類型的重要曲線（及曲面）不能用多項式精確表示，在系統(tǒng)中，這些曲線只能用多項式逼近。同一參數(shù)多項式曲線可以采用不同的基表示，如冪基表示和Bezier表示，由些決定了它們具有不同的性質(zhì)，因而就有不同的優(yōu)點。
二、 冪基曲線的計算 Calculate Polynomial Function
一條n次曲線的冪基表示形式是：
，其中
是矢量。
給定u0，計算冪基曲線上的點C（u0）的最有效算法是英國數(shù)學家W.G.Horner提出的Horner方法。Horner算法是遞歸概念的一個典型實例，它采用最少的乘法來進行多項式求值，使計算由X^n問題轉(zhuǎn)化為O（n）的問題。
l 當次數(shù)＝1時：
l 當次數(shù)＝2時：
l ……
l 當次數(shù)＝n時：
用數(shù)組來直接計算：
1 void Horner1(a, n, u0, C)
2 {
3 C = a[n];
4
5 for (int i = n-1; i >= 0; i--)
6 {
7 C = C * u0 + a[i];
8 }
9 }
10
在OpenSceneGraph中來計算：
1 void Horner(osg::Vec3Array* a, double u, osg::Vec3& p)
2 {
3 int n = a->size() - 1;
4
5 p = a->at(n);
6
7 for (int i = n-1; i >= 0; i--)
8 {
9 p = p * u + a->at(i);
10 }
11 }
三、 冪基曲線的顯示 Render Power Basis Curve
利用Horner方法可以計算[0,1]區(qū)間上相應(yīng)曲線上的點，將這些點連成線就構(gòu)成了冪基曲線的近似表示。在OpenSceneGraph中顯示冪基曲線程序如下所示：
1 /**
2 * Copyright (c) 2013 eryar All Rights Reserved.
3 *
4 * File : Main.cpp
5 * Author : eryar@163.com
6 * Date : 2013-05-06
7 * Version : 0.1
8 *
9 * Description : PLib means Polynomial functions library.
10 * The PLib in occ provides basic computation functions
11 * for polynomial functions.
12 *
13 */
14
15 // OpenSceneGraph
16 #include <osg/Vec3>
17 #include <osg/Array>
18 #include <osg/Geode>
19 #include <osg/Group>
20 #include <osg/MatrixTransform>
21 #include <osgGA/StateSetManipulator>
22 #include <osgViewer/Viewer>
23 #include <osgViewer/ViewerEventHandlers>
24
25 #pragma comment(lib, "osgd.lib")
26 #pragma comment(lib, "osgGAd.lib")
27 #pragma comment(lib, "osgViewerd.lib")
28
29 // OpenCascade
30 #include <PLib.hxx>
31 #include <TColgp_Array1OfPnt.hxx>
32 #include <TColStd_Array1OfReal.hxx>
33
34 #pragma comment(lib, "TKernel.lib")
35 #pragma comment(lib, "TKMath.lib")
36
37 /*
38 * @breif Compute point on power basis curve.
39 * @param [in] a:
40 * @param [in] x:
41 * @return: Point on power basis curve.
42 */
43 void Horner(osg::Vec3Array* a, double u, osg::Vec3& p)
44 {
45 int n = a->size() - 1;
46
47 if (-1 == n)
48 {
49 return ;
50 }
51
52 p = a->at(n);
53
54 for (int i = n-1; i >= 0; i--)
55 {
56 p = p * u + a->at(i);
57 }
58 }
59
60 osg::Node* RenderPowerBasisCurve()
61 {
62 const int nStep = 100;
63 osg::Geode* curveNode = new osg::Geode();
64 osg::ref_ptr<osg::Geometry> curveGeom = new osg::Geometry();
65 osg::ref_ptr<osg::Vec3Array> curvePnts = new osg::Vec3Array();
66
67 // Test to compuate point on power basis curve.
68 osg::ref_ptr<osg::Vec3Array> ctrlPnts = new osg::Vec3Array;
69 ctrlPnts->push_back(osg::Vec3(0, 0, 6));
70 ctrlPnts->push_back(osg::Vec3(3, 0, 6));
71 ctrlPnts->push_back(osg::Vec3(6, 0, 3));
72 //ctrlPnts->push_back(osg::Vec3(6, 0, 0));
73
74 for (int i = 0; i < nStep; i++)
75 {
76 osg::Vec3 pnt;
77 Horner(ctrlPnts, i * 1.0 / nStep, pnt);
78
79 curvePnts->push_back(pnt);
80 }
81
82 curveGeom->setVertexArray(curvePnts);
83 curveGeom->addPrimitiveSet(new osg::DrawArrays(osg::PrimitiveSet::LINE_STRIP, 0, curvePnts->size()));
84
85 curveNode->addDrawable(curveGeom);
86
87 return curveNode;
88 }
89
90 osg::Node* TestPLib(void)
91 {
92 const int nStep = 100;
93 osg::Geode* curveNode = new osg::Geode();
94 osg::ref_ptr<osg::Geometry> curveGeom = new osg::Geometry();
95 osg::ref_ptr<osg::Vec3Array> curvePnts = new osg::Vec3Array();
96
97 TColgp_Array1OfPnt poles(1, 3);
98 TColStd_Array1OfReal fp(1, poles.Length() * 3);
99 TColStd_Array1OfReal points(0, 1, 3);
100
101 Standard_Real* polynomialCoeff = (Standard_Real*) &(fp(fp.Lower()));
102 Standard_Real* result = (Standard_Real*)&(points(points.Lower()));
103
104 poles.SetValue(1, gp_Pnt(0, 0, 6));
105 poles.SetValue(2, gp_Pnt(3, 0, 6));
106 poles.SetValue(3, gp_Pnt(6, 0, 3));
107
108 // Change poles to flat array.
109 PLib::SetPoles(poles, fp);
110
111 // Three control point, so degree is 3-1=2.
112 Standard_Integer nDegree = 3 - 1;
113
114 // Because point are 3 Dimension.
115 Standard_Integer nDimension = 3;
116
117 for (int i = 0; i < nStep; i++)
118 {
119 PLib::NoDerivativeEvalPolynomial(
120 i * 1.0 / nStep,
121 nDegree,
122 nDimension,
123 nDegree * nDimension,
124 polynomialCoeff[0],
125 result[0]);
126
127 //
128 curvePnts->push_back(osg::Vec3(result[0], result[1], result[2]));
129 }
130
131 curveGeom->setVertexArray(curvePnts);
132 curveGeom->addPrimitiveSet(new osg::DrawArrays(osg::PrimitiveSet::LINE_STRIP, 0, curvePnts->size()));
133
134 curveNode->addDrawable(curveGeom);
135
136 return curveNode;
137 }
138
139 int main(int argc, char* argv[])
140 {
141 osgViewer::Viewer myViewer;
142 osg::ref_ptr<osg::Group> root = new osg::Group();
143
144 root->addChild(RenderPowerBasisCurve());
145
146 // Translate along x axis.
147 osg::ref_ptr<osg::MatrixTransform> transform = new osg::MatrixTransform();
148 transform->setMatrix(osg::Matrix::translate(1, 0, 0));
149 transform->addChild(TestPLib());
150
151 root->addChild(transform);
152
153 myViewer.setSceneData(root);
154
155 myViewer.addEventHandler(new osgGA::StateSetManipulator(myViewer.getCamera()->getOrCreateStateSet()));
156 myViewer.addEventHandler(new osgViewer::StatsHandler);
157 myViewer.addEventHandler(new osgViewer::WindowSizeHandler);
158
159 return myViewer.run();
160 }
161
設(shè)置不同的控制點ctrlPnts，就得到不同的曲線。
當n=1時，有兩個控制點a0, a1，表示由a0到a0+a1的直線段，如圖3.1所示：
Figure 3.1 連接兩點（0,0,6）到（3,0,6）的直線
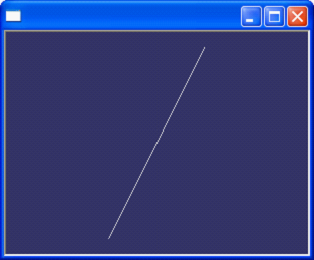
當n=2時，曲線是一段由a0到a0+a1+a2的拋物線弧，如圖3.2所示：
Figure 3.2 拋物線弧（0,0,6）（3,0,6）（6,0,3）
四、 occ中的多項式計算庫The PLib in OCC
在OpenCascade中的基礎(chǔ)模塊（FoundationClasses）的數(shù)學計算工具箱（TKMath Toolkit）中有個PLib包，用以對多項式進行基本的計算。PLib庫中的函數(shù)都是靜態(tài)函數(shù)，所以都是類函數(shù)，可以用類名加函數(shù)名直接調(diào)用。
PLib可對多項式進行如下計算：
l 計算多項式的值：EvalPolynomial；
l 計算Lagrange插值：EvalLagrange；
l 計算Hermite插值：EvalCubicHermite；
其中計算多項式值的方法也是用的Horner方法。
包PLib中提供了計算幾何的數(shù)學基礎(chǔ)中多項式插值中大部分插值計算。結(jié)合書籍《計算幾何教程》科學出版社中第一章的理論內(nèi)容及OpenCascade的源程序，可以方便計算幾何的數(shù)學基礎(chǔ)知識的學習。
五、 使用PLib Apply PLib Class
因為包PLib中的類PLib都是靜態(tài)函數(shù)，所以函數(shù)傳入的參數(shù)比較多，若要使用這些計算函數(shù)，需要對其函數(shù)參數(shù)進行了解。為了對不同維數(shù)多項式進行計算，類PLib中把空間點轉(zhuǎn)換成了實數(shù)數(shù)組，并提供了相互轉(zhuǎn)換的函數(shù)。以計算多項式值為例，來說明使用PLib的方法。程序代碼如下所示：
1 osg::Node* TestPLib(void)
2 {
3 const int nStep = 100;
4 osg::Geode* curveNode = new osg::Geode();
5 osg::ref_ptr<osg::Geometry> curveGeom = new osg::Geometry();
6 osg::ref_ptr<osg::Vec3Array> curvePnts = new osg::Vec3Array();
7
8 TColgp_Array1OfPnt poles(1, 3);
9 TColStd_Array1OfReal fp(1, poles.Length() * 3);
10 TColStd_Array1OfReal points(0, 1, 3);
11
12 Standard_Real* polynomialCoeff = (Standard_Real*) &(fp(fp.Lower()));
13 Standard_Real* result = (Standard_Real*)&(points(points.Lower()));
14
15 poles.SetValue(1, gp_Pnt(0, 0, 6));
16 poles.SetValue(2, gp_Pnt(3, 0, 6));
17 poles.SetValue(3, gp_Pnt(6, 0, 3));
18
19 // Change poles to flat array.
20 PLib::SetPoles(poles, fp);
21
22 // Three control point, so degree is 3-1=2.
23 Standard_Integer nDegree = 3 - 1;
24
25 // Because point are 3 Dimension.
26 Standard_Integer nDimension = 3;
27
28 for (int i = 0; i < nStep; i++)
29 {
30 PLib::NoDerivativeEvalPolynomial(
31 i * 1.0 / nStep,
32 nDegree,
33 nDimension,
34 nDegree * nDimension,
35 polynomialCoeff[0],
36 result[0]);
37
38 //
39 curvePnts->push_back(osg::Vec3(result[0], result[1], result[2]));
40 }
41
42 curveGeom->setVertexArray(curvePnts);
43 curveGeom->addPrimitiveSet(new osg::DrawArrays(osg::PrimitiveSet::LINE_STRIP, 0, curvePnts->size()));
44
45 curveNode->addDrawable(curveGeom);
46
47 return curveNode;
48 }
函數(shù)PLib::SetPoles可以將空間坐標點轉(zhuǎn)換為實數(shù)數(shù)組。在調(diào)用無微分計算多項式的函數(shù)時，將坐標點的實數(shù)數(shù)組的首地址作為參數(shù)之一傳入。
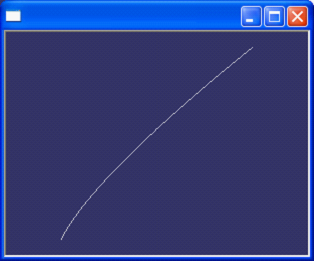
為了與前面的Horner方法計算多項式的結(jié)果進行對比，將OpenCascade對相同點計算的結(jié)果也顯示出來。如下圖5.1所示：
Figure 5.1 PLib compute result VS. Previous Horner method
由上圖可知，PLib的計算結(jié)果與前面的Horner方法計算結(jié)果相同。查看OpenCascade的源程序，得其多項式計算方法也是采用的Horner方法。
1 void PLib::NoDerivativeEvalPolynomial(const Standard_Real Par,
2
3 const Standard_Integer Degree,
4
5 const Standard_Integer Dimension,
6
7 const Standard_Integer DegreeDimension,
8
9 Standard_Real& PolynomialCoeff,
10
11 Standard_Real& Results)
12
13 {
14
15 Standard_Integer jj;
16
17 Standard_Real *RA = &Results ;
18
19 Standard_Real *PA = &PolynomialCoeff ;
20
21 Standard_Real *tmpRA = RA;
22
23 Standard_Real *tmpPA = PA + DegreeDimension;
24
25 switch (Dimension) {
26
27 case 1 : {
28
29 *tmpRA = *tmpPA;
30
31 for (jj = Degree ; jj > 0 ; jj--) {
32
33 tmpPA--;
34
35 *tmpRA = Par * (*tmpRA) + (*tmpPA);
36
37 }
38
39 break;
40
41 }
42
43 }
44
45
從上述計算一維多項式的代碼可以看出，計算方法與前面的Horner方法相同。
六、 結(jié)論
學習使用Horner方法來計算多項式的值，并將計算結(jié)果在OpenSceneGraph中顯示。通過使用OpenCascade的多項式庫PLib來計算多項式的值，并結(jié)合其源程序來理解如何使用庫PLib。庫PLib為了統(tǒng)一多項式的計算，將空間點都轉(zhuǎn)換成數(shù)組后再進行計算，在這其中大量使用了指針，代碼可讀性也不是很好，需要仔細、耐心。
七、 參考資料
1. 王仁宏、李崇君、朱春鋼 計算幾何教程 科學出版社 2008.6
2. 趙罡、穆國旺、王拉柱 非均勻有理B樣條《The NURBS Book》 清華大學出版社 2010.12
3. OpenCascade source code