Make Helix Curve in OpenCASCADE
eryar@163.com
Abstract. OpenCASCADE does not provide helix curve directly, but you can build a helix curve by the pcurve of a surface(curve on surface). When you understand the pcurve of a surface, you can make a helix curve easily. The paper first make a helix by Tcl in Draw Test Harness, then translate the Tcl script to OpenCASCADE C++ code.
Key Words. OpenCASCADE, Helix Curve, PCurve, Sweep, Spring
1. Introduction
螺旋線是實(shí)踐中常用到的曲線,例如平頭螺絲釘?shù)耐饩壡€就是螺旋線。當(dāng)我們擰緊平頭螺絲釘時(shí),它的外緣曲線上的任一點(diǎn)M一方面繞螺絲釘?shù)妮S旋轉(zhuǎn),另一方面又沿平行于軸線的方向前進(jìn),點(diǎn)M就走出一段螺旋線。[1]
如果空間一點(diǎn)M在圓柱面x*x+y*y=a*a上以角速度ω繞z軸旋轉(zhuǎn),同時(shí)又以線速度υ沿平等于z軸正方向上升(其中ω,υ都是常數(shù)),那未點(diǎn)M構(gòu)成的圖形叫螺旋線。其參數(shù)方程為:
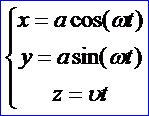
Figure 1.1 A Helix Curve
OpenCASCADE中并沒有直接提供構(gòu)造螺旋線的類和函數(shù),因此只有自己來構(gòu)造了,其中構(gòu)造的核心是要理解PCurve(曲面的參數(shù)曲線)。本文先以Tcl腳本在Draw Test Harness中快速生成一個(gè)螺旋線,再將相應(yīng)的Tcl腳本轉(zhuǎn)換成C++代碼。在理解Pcurve概念的基礎(chǔ)上來構(gòu)造螺旋線還是很簡單的,甚至還可以擴(kuò)展應(yīng)用。
2.Make Helix Curve
在OpenCASCADE提供的一個(gè)經(jīng)典例子:生成一個(gè)酒瓶中,就有螺旋線的應(yīng)用,即生成瓶口處的螺紋。當(dāng)時(shí)看這例子的時(shí)候也是沒有完全理解,究竟怎么生成的那個(gè)螺旋線?感謝lifenli的提醒,使我又重溫了一遍例子,頓時(shí)茅塞頓開,明白了pcurve的一個(gè)應(yīng)用。
由《OpenCASCADE BRep Format》[4]中可知,圓柱面的參數(shù)方程為:
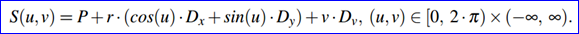
假設(shè)當(dāng)你在參數(shù)空間[u,v]中創(chuàng)建一條二維曲線后,可根據(jù)這個(gè)二維曲線來計(jì)算對應(yīng)曲面上的三維曲線。根據(jù)二維曲線的不同定義,得到的結(jié)果如下:
條件 | 參數(shù)方程 | 參數(shù)曲線 |
U=0 | S(v)=P+r*cos(u)+vDz | 與Z軸平行的直線 |
V=0 | S(u)=P+r*(cos(u)*Dx+sin(u)*Dy) | 與XOY面平行的圓 |
U!=0 && V != 0 | S(u,v)=P+r(cos(u)*Dx+sin(u)*Dy)+vDz | 螺旋線 |
對比螺旋線的參數(shù)方程可知,當(dāng)參數(shù)空間中的u和v都不為0時(shí),得到的圓柱面上的線就是螺旋線。考慮最簡單的情況,那就是u=v,即在參數(shù)空間中是一條斜率k=1的直線。在OpenCASCADE的Draw Test Harness用Tcl腳本測試,Tcl腳本如下所示:
#
# make helix curve in OpenCASCADE.
# Shing Liu(eryar@163.com)
# 2015-07-08 22:00
#
pload MODELING VISUALIZATION
cylinder aCylinder 6
line aLine2d 0 0 1 1
trim aSegment aLine2d 0 2*pi
mkedge aHelixEdge aSegment aCylinder 0 6*pi
vdisplay aHelixEdge
代碼先加載所需的造型及顯示模塊,然后創(chuàng)建一個(gè)圓柱面aCylinder;一條二維直線aLine2d;再將參數(shù)范圍限定在0到2PI之間;最后使用了用曲面及其上的pcurve來創(chuàng)建邊的算法mkedge生成了螺旋線并顯示在三維窗口中。
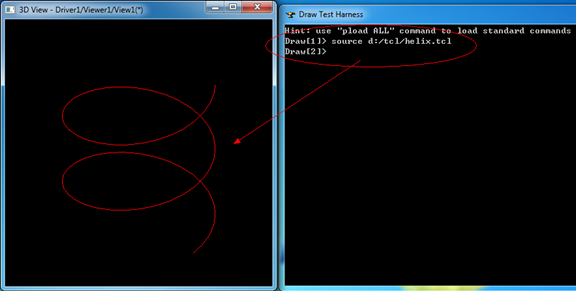
Figure 2.1 Make a helix by Tcl script
上述Tcl腳本可以很容易的轉(zhuǎn)換成C++代碼的,下面給出相應(yīng)的C++實(shí)現(xiàn),源碼如下所示:
#define WNT
#include <gp_Lin2d.hxx>
#include <GCE2d_MakeSegment.hxx>
#include <Geom_CylindricalSurface.hxx>
#include <BRepBuilderAPI_MakeEdge.hxx>
#include <TopoDS_Edge.hxx>
#include <BRepTools.hxx>
#pragma comment(lib, "TKernel.lib")
#pragma comment(lib, "TKMath.lib")
#pragma comment(lib, "TKG3d.lib")
#pragma comment(lib, "TKBRep.lib")
#pragma comment(lib, "TKGeomBase.lib")
#pragma comment(lib, "TKTopAlgo.lib")
void makeHelix(void)
{
Handle_Geom_CylindricalSurface aCylinder = new Geom_CylindricalSurface(gp::XOY(), 6.0);
gp_Lin2d aLine2d(gp_Pnt2d(0.0, 0.0), gp_Dir2d(1.0, 1.0));
Handle_Geom2d_TrimmedCurve aSegment = GCE2d_MakeSegment(aLine2d, 0.0, M_PI * 2.0);
TopoDS_Edge aHelixEdge = BRepBuilderAPI_MakeEdge(aSegment, aCylinder, 0.0, 6.0 * M_PI).Edge();
BRepTools::Dump(aHelixEdge, std::cout);
BRepTools::Write(aHelixEdge, "d:/helix.brep");
}
int main(int argc, char* argv[])
{
makeHelix();
return 0;
}
由C++代碼可知,生成螺旋線的關(guān)鍵是在生成邊的時(shí)候,將pcurve和相應(yīng)的曲面及其參數(shù)范圍一起傳給了生成邊的類,這樣就得到拓樸邊了。如果想要得到幾何的螺旋線,可以使用工具BRep_Tool::Curve()來將拓樸邊中的幾何曲線提取出來。經(jīng)過測試,用pcurve生成的Edge中沒有三維幾何曲線,不過occ提供了一個(gè)靜態(tài)函數(shù)來將pcurve對應(yīng)的三維曲線擬合成nurbs曲線,函數(shù)為:BRepLib::BuildCurve3d();
參數(shù)空間中pcurve的斜率決定了螺旋線的螺距pitch,當(dāng)其他參數(shù)不變,改變斜率后得到如下圖所示結(jié)果:
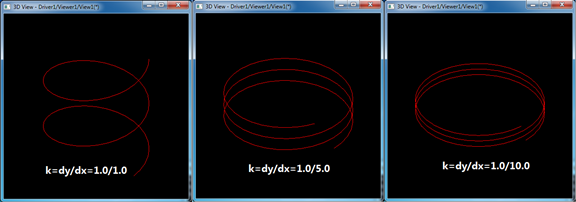
Figure 2.2 Different Pitch by different K
由圖可知,當(dāng)pcurve的斜率越小時(shí),得到的螺旋線的螺距也越小。修改pcurve的斜率只需要修改上述Tcl腳本中的aLine2d的斜率。
如當(dāng)斜率k=1時(shí)的pcurve為:
line aLine2d 0 0 1 1
當(dāng)斜率k=1.0/5.0時(shí)的pcurve為:
line aLine2d 0 0 5 1
當(dāng)斜率k=1.0/10.0時(shí)的pcurve為:
line aLine2d 0 0 10 1
可以自己嘗試修改看看沒的斜率得到的不同螺旋線的螺距變化。
3.Spring: Sweep profile along helix
得到螺旋線后自然就想到能不能用一個(gè)圓沿著螺旋線來放樣,從而得到一個(gè)彈簧。下面還是用Tcl腳本在Draw Test Harness中嘗試一下,相應(yīng)的C++實(shí)現(xiàn)也是很容易找到相關(guān)的類。
#
# make helix curve in OpenCASCADE.
# Shing Liu(eryar@163.com)
# 2015-07-08 22:00
#
pload MODELING VISUALIZATION
cylinder aCylinder 6
line aLine2d 0 0 1 1
trim aSegment aLine2d 0 2*pi
mkedge aHelixEdge aSegment aCylinder 0 6*pi
# there is no curve 3d in the pcurve edge.
mkedgecurve aHelixEdge 0.001
wire aHelixWire aHelixEdge
circle profile 6 0 0 0 4 1 1
mkedge profile profile
wire profile profile
mkplane profile profile
pipe aSpring aHelixWire profile
vdisplay aSpring
vsetmaterial aSpring steel
vsetgradientbg 180 200 255 180 180 180 2
vsetdispmode 1
vzbufftrihedron
# set ray tracing
if { ! [catch {vrenderparams -raytrace -shadows -reflections -fsaa -rayDepth 5}] } {
vtextureenv on 1
}
生成效果如下圖所示:
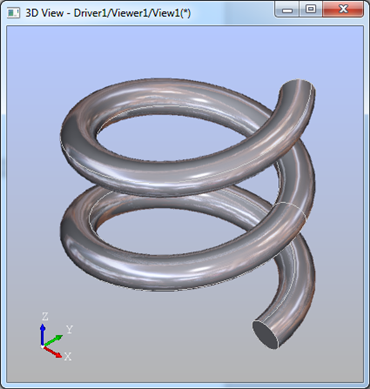
Figure 3.1 Spring by sweep a circle along a helix path
當(dāng)將pcruve在圓錐面上生成三維曲線時(shí)就會(huì)得到類似夏天的蚊香那樣螺旋形狀。同樣使用上述代碼,只是將圓柱面改成圓錐面得到:
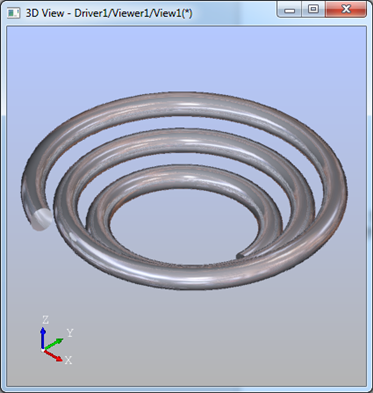
Figure 3.2 Mosquito Coil
4.Conclusion
綜上所述,常見的計(jì)算幾何造型書中講到曲線的參數(shù)方程都會(huì)以螺旋線為經(jīng)典例子,甚至是高等數(shù)學(xué)中也是一樣,由此可見螺旋線是很常見的一種曲線。但是occ中并沒有直接提供螺旋線的幾何曲線,只有通過pcurve來構(gòu)造了。所以理解pcurve后,才好理解make bottle例子中的瓶頸螺紋部分的代碼。
通過將一個(gè)輪廓沿著螺旋線掃掠可以得出很多有意思的模型。在使用sweep的過程中發(fā)現(xiàn)pcurve生成的邊Edge中并沒有三維幾何曲線,所以會(huì)導(dǎo)致算法失敗。最終發(fā)現(xiàn)occ提供了一個(gè)將pcurve生成的邊中生成出一個(gè)擬合三維幾何曲線的函數(shù)BRepLib::BuildCurve3d()。對于一些在曲面上的曲線的造型可以參考這種用法,用pcurve來構(gòu)造。
5. References
1. 同濟(jì)大學(xué)數(shù)學(xué)教研室. 高等數(shù)學(xué)(上). 高等教育出版社. 1978
2. Helix. http://mathworld.wolfram.com/Helix.html
3. OpenCASCADE Make Bottle Tutorial. 2015
4. OpenCASCADE BRep Format. 2015
5. 莫勇,常智勇. 計(jì)算機(jī)輔助幾何造型技術(shù). 科學(xué)出版社. 2009