Visualize Surface by Delaunay Triangulator
eryar@163.com
Abstract. Delaunay Triangulation is the core algorithm for mesh generation. By Delaunay Triangulator you can make a general method to visualize geometry surfaces, so does OpenCascade. The paper focus on the geometry surfaces visualization, include the surfaces with holes.
Key words. OpenCascade, Delaunay Triangulator, OpenSceneGraph, Mesh, NURBS
1. Introduction
模型數據最終要在顯示器上輸出,需要有統一的處理方法。對于曲線而言,只需要在曲線上取一定的點連接成線,就可以用來逼近顯示曲線了。對于曲面而言,可以用三角網格來逼近曲面。對于參數表示的曲線,求曲線的點很容易,只要給出參數就可以得到參數對應的曲線上的點。對于參數表示的曲面,情況要復雜些了,如何得到三角網格呢?
經過boolean operation后,會有些孔產生,這些面上的孔如何用統一的方法可視化呢?對于曲面的可視化也一定存在統一、簡單的方法。程序開發最終追求的都是簡單、統一,這樣代碼才顯得優雅。如果代碼看上去很復雜,到處是重復代碼,暴露出來的接口也很隨意,完全違背單一職責原則和Demeter法則,開發出來的軟件用起來必定也很麻煩,這對程序員和軟件用戶都是噩夢。這樣的代碼一定有重構和改進的空間,最終達到程序開發人員和軟件的用戶都舒服的狀態。書山有路勤為徑,學海無涯苦作舟,拒絕保守、懶惰,不思進取。
言歸正傳,本文主要使用OpenSceneGraph中的Delaunay Triangulator來對OpenCascade中的任意參數曲面可視化,即曲面可視化的統一算法。在理解曲面可視化的基礎上,可對NURBS曲面的可視化,有助于直觀來學習NURBS理論。
談到NURBS理論,又是追求統一、簡單的產物。由于在數學和算法上的良好性質,以及在工業領域的成功應用,使得NURBS得到了極大的普及。NURBS在CAD/CAM/CAE領域中所起的作用類似于英語在科學和商業中的作用。因此,想從事CAD,必須理解NURBS。NURBS的重要作用就是統一了曲線曲面的數學模型,使軟件對曲線曲面的處理方式相同,且利用NURBS進行設計非常直觀,幾乎每個工具和算法都有一個易于理解的幾何解釋。
讓CAD軟件用戶使用簡單,得到便利,就要有相應的技術(NURBS)支持。至于NURBS是Non-Uniform Rational B-Spline還是Nobody Understands Rational B-Spline,普通用戶是不關心的。網格化的算法也是類似,讓三維模型可視化變得簡單、統一,至于是使用Delaunay Triangulation還是其他算法,對于圖形顯示接口如OpenGL也不關心,他只管畫三角形就好。然而高效的網格化算法也是一個技術難點。如果不僅要知其然而且還要知其所以然,都要付出努力。
2. Visualize Geometry Surface
網格生成技術是研究如何將給定的空間離散為簡單的幾何單元的方法。三角網格和四面體網格是迄今為止最為常用的非結構形式,它可以很好地逼近邊界,描述結構復雜的空間。Delaunay三角、四面體剖分由于其具有良好的數學基礎,對網格的局部控制能力強,網格單元自動向正三角、四面體逼近等優良特性,近年來受到了眾多領域的研究人員的關注,在科學計算可視化、圖形學三維表示、石油地質勘探、地理信息系統、逆向工程、醫學圖像處理等領域有著明顯的應用前景。
在數字地形建模中,不規則三角網(TIN)通過從不規則離散分布的數據點生成的連續三角面來逼近地形表面。就表達地形信息角度而言,TIN模型的優點是它能以不同層次的分辨率來描述地形表面。TIN模型在一定特定分辨率下能用更少的空間和時間更精確地表示復雜的表面。特別是當地形包含有大量特征,如斷裂線、構造線時,TIN模型能更好地顧及這些特征,從而更精確地表達地表形態。關于Delaunay算法,可以參考相關書籍或網絡資源自己實現,或是使用開源庫,如Triangle, CGAL等。本文主要是使用OpenSceneGraph中現成算法來將參數曲面可視化。
OpenSceneGraph中Delaunay的使用非常簡單,只需要將點集傳給DelaunayTriangulator即可,下面代碼示例將OpenCascade中任意參數曲面的參數空間離散成三角網格,再映射到三維空間,將曲面可視化。
osg::Node* BuildSurface(const Handle_Geom_Surface &theSurface)
{
osg::ref_ptr<osg::Geode> aGeode = new osg::Geode();
osg::ref_ptr<osg::Geometry> aGeometry = new osg::Geometry();
osg::ref_ptr<osg::Vec3Array> aUVPoints = new osg::Vec3Array();
osg::ref_ptr<osg::Vec3Array> aPoints = new osg::Vec3Array();
osg::ref_ptr<osgUtil::DelaunayTriangulator> dt = new osgUtil::DelaunayTriangulator();
// build triangulation for the parametric space.
Standard_Real u1 = 0.0;
Standard_Real u2 = 0.0;
Standard_Real v1 = 0.0;
Standard_Real v2 = 0.0;
theSurface->Bounds(u1, u2, v1, v2);
Precision::IsNegativeInfinite(u1) ? u1 = -1.0: u1;
Precision::IsPositiveInfinite(u2) ? u2 = 1.0: u2;
Precision::IsNegativeInfinite(v1) ? v1 = -1.0: v1;
Precision::IsPositiveInfinite(v2) ? v2 = 1.0: v2;
// tesselate the parametric space.
Standard_Integer aStep = 30;
Standard_Real uDelta = (u2 - u1) / aStep;
Standard_Real vDelta = (v2 - v1) / aStep;
for (Standard_Integer i = 0; i <= aStep; ++i)
{
for (Standard_Integer j = 0; j <= aStep; ++j)
{
Standard_Real u = u1 + i * uDelta;
Standard_Real v = v1 + j * vDelta;
aUVPoints->push_back(osg::Vec3(u, v, 0.0));
}
}
// triangulate the parametric space.
dt->setInputPointArray(aUVPoints);
dt->triangulate();
for (osg::Vec3Array::const_iterator j = aUVPoints->begin(); j != aUVPoints->end(); ++j)
{
// evaluate the point on the surface
gp_Pnt aPoint = theSurface->Value((*j).x(), (*j).y());
aPoints->push_back(osg::Vec3(aPoint.X(), aPoint.Y(), aPoint.Z()));
}
//aGeometry->setVertexArray(aUVPoints);
aGeometry->setVertexArray(aPoints);
aGeometry->addPrimitiveSet(dt->getTriangles());
aGeode->addDrawable(aGeometry);
// use smoothing visitor to set the average normals
osgUtil::SmoothingVisitor sv;
sv.apply(*aGeode);
// set material for the surface
osg::ref_ptr<osg::StateSet> aStateSet = aGeode->getOrCreateStateSet();
osg::ref_ptr<osg::Material> aMaterial = new osg::Material();
aMaterial->setDiffuse(osg::Material::FRONT, osg::Vec4(1.0f, 1.0f, 0.0f, 1.0f));
aMaterial->setSpecular(osg::Material::FRONT, osg::Vec4(1.0f, 1.0f, 1.0f, 1.0f));
aMaterial->setShininess(osg::Material::FRONT, 100.0f);
aStateSet->setAttribute(aMaterial);
return aGeode.release();
}
為了與另一篇blog中的區別,在OpenSceneGraph中繪制OpenCascade的曲面: http://www.shnenglu.com/eryar/archive/2013/08/11/202466.html
特意加上了材質和光照效果。離散的曲面效果如下圖所示:
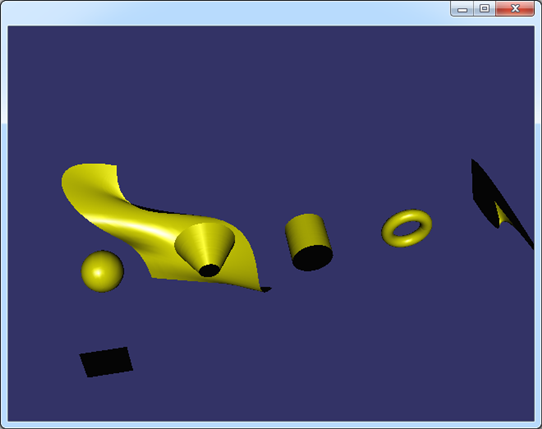
Figure 2.1 Shaded Surfaces in OpenSceneGraph
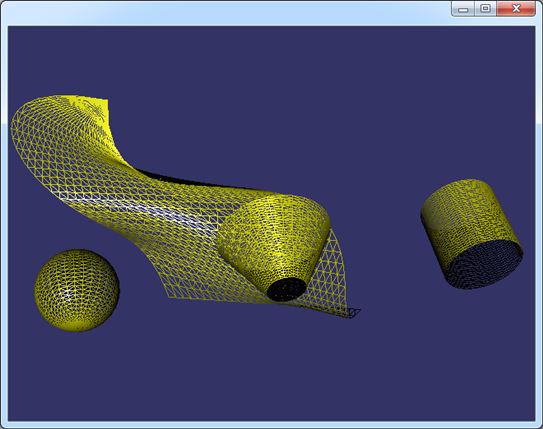
Figure 2.2 Mesh of the Surfaces in OpenSceneGraph
為了顯示出光照效果,使用了osgUtil::SmoothingVisitor來自動計算三角網格的平均法向。從上圖可知,這種方式是將曲面的參數空間均勻剖分得到的曲面,當剖分得密時,數據量大,但顯示得逼真。剖分疏時,數據量小,顯示失真。
利用特征敏感網格重剖技術,可以使用較少的三角面片來比較精確地表示幾何模型,如下圖所示:(圖片來源:http://cg.cs.tsinghua.edu.cn/papers/TVCG2007featuresensitive.pdf)
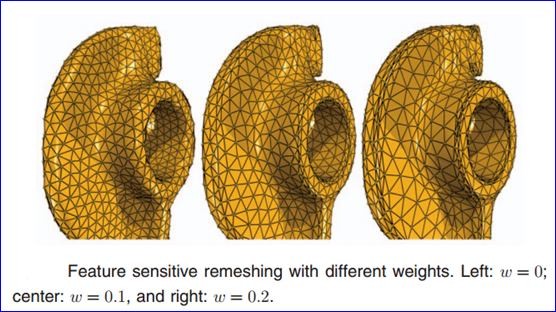
Figure 2.3 Feature sensitive remeshing (http://cg.cs.tsinghua.edu.cn/)
3. Holes in the Surface
當曲面上有開孔時,開孔的信息可以通過WIRE來獲得。對于組成開孔的WIRE的每條EDGE,可以通過曲面上的曲線PCurve來將開孔的參數統一到曲面的UV參數空間。
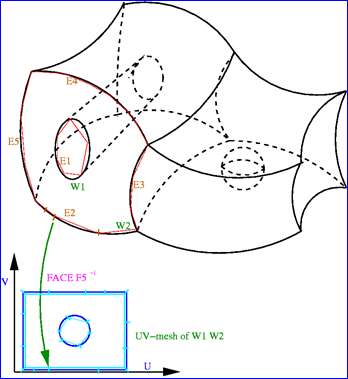
Figure 3.1 Hole in Parametric UV space
在OpenSceneGraph中實現代碼如下所示:
osg::Node* BuildSurface(const Handle_Geom_Surface &theSurface, const Handle_Geom2d_Curve &thePCurve)
{
osg::ref_ptr<osg::Geode> aGeode = new osg::Geode();
osg::ref_ptr<osg::Geometry> aGeometry = new osg::Geometry();
osg::ref_ptr<osg::Vec3Array> aUVPoints = new osg::Vec3Array();
osg::ref_ptr<osg::Vec3Array> aPoints = new osg::Vec3Array();
osg::ref_ptr<osg::Vec3Array> aBounds = new osg::Vec3Array();
osg::ref_ptr<osgUtil::DelaunayTriangulator> dt = new osgUtil::DelaunayTriangulator();
osg::ref_ptr<osgUtil::DelaunayConstraint> dc = new osgUtil::DelaunayConstraint();
// build triangulation for the parametric space.
Standard_Real u1 = 0.0;
Standard_Real u2 = 0.0;
Standard_Real v1 = 0.0;
Standard_Real v2 = 0.0;
theSurface->Bounds(u1, u2, v1, v2);
Precision::IsNegativeInfinite(u1) ? u1 = -1.0: u1;
Precision::IsPositiveInfinite(u2) ? u2 = 1.0: u2;
Precision::IsNegativeInfinite(v1) ? v1 = -1.0: v1;
Precision::IsPositiveInfinite(v2) ? v2 = 1.0: v2;
// tesselate the parametric space.
Standard_Integer aStep = 30;
Standard_Real uDelta = (u2 - u1) / aStep;
Standard_Real vDelta = (v2 - v1) / aStep;
for (Standard_Integer i = 0; i <= aStep; ++i)
{
for (Standard_Integer j = 0; j <= aStep; ++j)
{
Standard_Real u = u1 + i * uDelta;
Standard_Real v = v1 + j * vDelta;
aUVPoints->push_back(osg::Vec3(u, v, 0.0));
}
}
Standard_Real pDelta = (thePCurve->LastParameter() - thePCurve->FirstParameter()) / aStep;
for (Standard_Integer c = 0; c <= aStep; ++c)
{
gp_Pnt2d p = thePCurve->Value(thePCurve->FirstParameter () + c * pDelta);
aBounds->push_back(osg::Vec3(p.X(), p.Y(), 0.0));
}
dc->setVertexArray(aBounds);
dc->addPrimitiveSet(new osg::DrawArrays(osg::PrimitiveSet::LINE_LOOP, 0, aBounds->size()));
// triangulate the parametric space.
dt->addInputConstraint(dc);
dt->setInputPointArray(aUVPoints);
dt->triangulate();
dt->removeInternalTriangles(dc);
for (osg::Vec3Array::const_iterator j = aUVPoints->begin(); j != aUVPoints->end(); ++j)
{
// evaluate the point on the surface
gp_Pnt aPoint = theSurface->Value((*j).x(), (*j).y());
aPoints->push_back(osg::Vec3(aPoint.X(), aPoint.Y(), aPoint.Z()));
}
//aGeometry->setVertexArray(aUVPoints);
aGeometry->setVertexArray(aPoints);
aGeometry->addPrimitiveSet(dt->getTriangles());
aGeode->addDrawable(aGeometry);
// use smoothing visitor to set the average normals
osgUtil::SmoothingVisitor sv;
sv.apply(*aGeode);
// set material for the surface
osg::ref_ptr<osg::StateSet> aStateSet = aGeode->getOrCreateStateSet();
osg::ref_ptr<osg::Material> aMaterial = new osg::Material();
aMaterial->setDiffuse(osg::Material::FRONT, osg::Vec4(1.0f, 1.0f, 0.0f, 1.0f));
aMaterial->setSpecular(osg::Material::FRONT, osg::Vec4(1.0f, 1.0f, 1.0f, 1.0f));
aMaterial->setShininess(osg::Material::FRONT, 100.0f);
aStateSet->setAttribute(aMaterial);
return aGeode.release();
}
開孔的實現主要也是用osgUtil::DelaunayConstraint,將孔中的三角形去除。如下圖所示為在球面和錐面開孔:
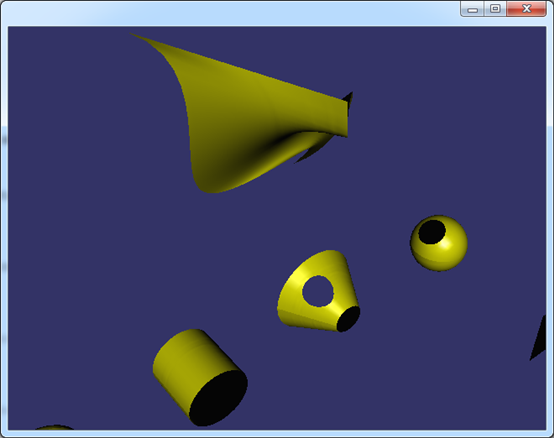
Figure 3.2 Holes on Sphere and Cone Surface
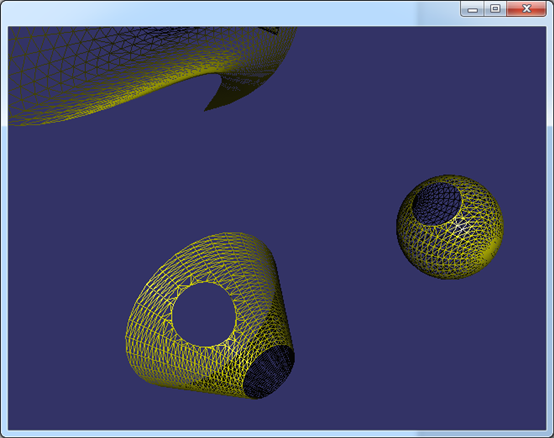
Figure 3.3 Mesh for Sphere and Cone with holes
由上圖可知,對于有拓樸結構的三維模型數據,可以由WIRE得到組成孔的每條邊Edge,根據Edge中PCurve可以找到對應的曲面。通過PCurve將開孔數據統一到參數空間中。剖分完帶孔的參數空間,再映射回三維空間就得到開孔的曲面了。
4. Conclusion
原來一直百思不得其解的問題現在已經豁然開朗,對三維模型的可視化有了一定的理解。借助于這些開源庫,對相關知識的學習要輕松許多,可以將許多國產教材上斷續的理論知識與實踐銜接起來。
5. Acknowledgement
感謝OpenCascade和OpenSceneGraph的開放和分享,讓學習變得輕松有趣。
6. Reference
1. 孫家廣, 胡事民等. 計算機圖形學. 清華大學出版社. 2000
2. 趙罡, 穆國旺, 王拉柱譯. 非均勻有理B樣條. 清華大學出版社. 2010
3. Jonathan R. Shewchuk. Triangle: http://www.cs.cmu.edu/~quake/triangle.html
4. 汪嘉業 王文平 屠長河 楊承磊. 計算幾何及應用. 科學出版社. 2011
5. 王成恩. 面向科學計算的網格劃分與可視化技術. 科學出版社. 2011
6. 周培德. 計算幾何-算法設計與分析. 清華大學出版社. 2008
7. http://cg.cs.tsinghua.edu.cn/
8. Mesh Algorithm in OpenCascade:
http://www.shnenglu.com/eryar/archive/2014/04/06/206484.html