OpenCascade Primitives BRep - Sphere
eryar@163.com
Abstract. BRep is short for Boundary Representation. Boundary Representation gives a complete description of an object by associating topological and geometric information for solid modeling. In this case, objects are described by their boundaries. There are two types of information in BRep: Topological information and Geometric information. This paper is concerned with the sphere BRep in OpenCascade, and also show how to use Tcl script to dump sphere BRep info.
Key words. OpenCascade, BRep, Boundary Representation, Sphere, Singularity
1. Introduction
球體的幾何數(shù)據(jù)主要是一個球面,在OpenCascade中球面的參數(shù)方程如下所示:
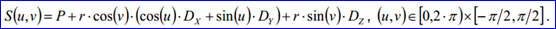
在《Parametric Curves and Surfaces》一文中,對參數(shù)曲線曲面進行了介紹,并重點介紹了球面的奇異性(Singularity)。本文通過對Sphere的BRep表示進行分析,來理解邊界表示法中對參數(shù)曲面上奇點(Singular Point)的處理及BRep_TEdge中包含的多種形式的曲線。
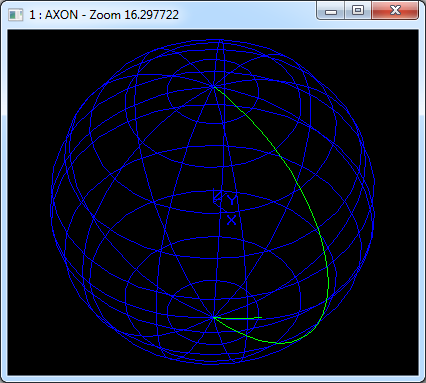
Figure 1.1 Sphere Generated by Tcl in Draw Test Harness
2. Dump Sphere BRep Info by Tcl
在OpenCascade中使用Tcl腳本來測試一些想法真是很方便,如這里要輸出球的邊界表示的數(shù)據(jù),只需要三條命令就可以完成。以下Tcl命令生成了一個圓心在原點(0,0,0),半徑為10的球:
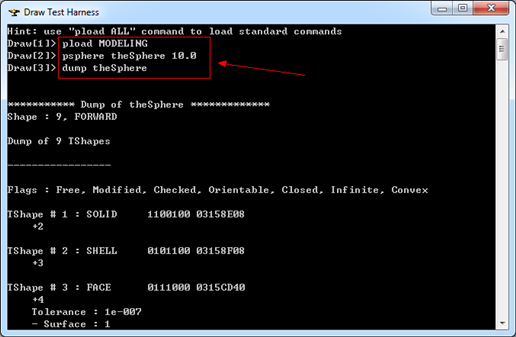
Figure 2.1 Dump Sphere BRep Info in Draw Test Harness
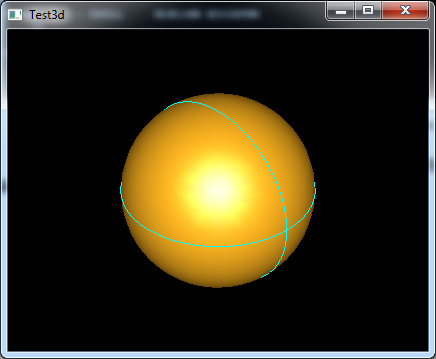
Figure 2.2 Display the Sphere in Draw
與《OpenCascade Primitives BRep - Box》一樣,根據(jù)這些信息,從Vertex開始編號,來分析球的BRep表示。
3. Sphere BRep in OpenCascade
球的拓樸頂點Vertex有兩個,分別是#7(0, 0, -10)和#9(0, 0, 10),如下圖所示:
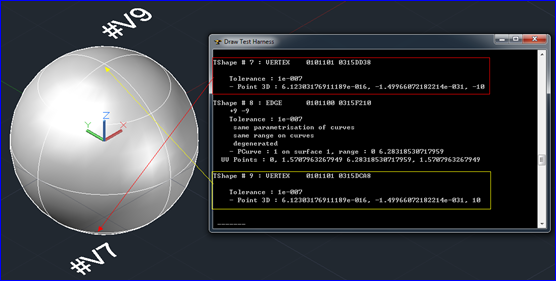
Figure 3.1 Vertex of Sphere BRep in OpenCascade
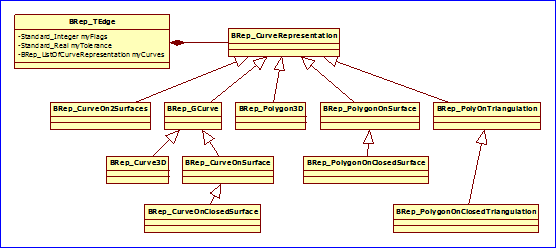
Figure 3.2 Curve Representation of BRep_TEdge
邊Edge有三種表現(xiàn)形式,分別是#5,#6和#8,其中#5和#8是退化邊(Degenerated Edge),即球面參數(shù)方程的奇點(Singular Point),在前文《PCurve - Curve on Surface》中分析曲面上曲線PCurve時已經(jīng)討論過,此處略過。本文只對#6邊中的幾何信息進行詳細分析。
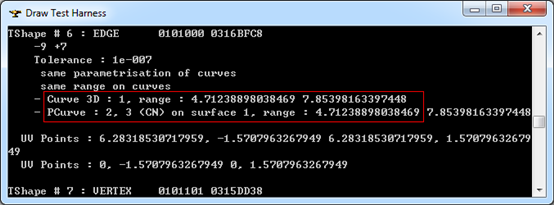
Figure 3.3 Edge #6 of Sphere BRep in OpenCascade
從拓樸邊中可以看出#6Edge中的曲線有三個:一是三維空間曲線(Curve 3D)1;另外兩個是曲面上曲線。其中三維空間曲線1的參數(shù)方程及其參數(shù)如下圖所示:
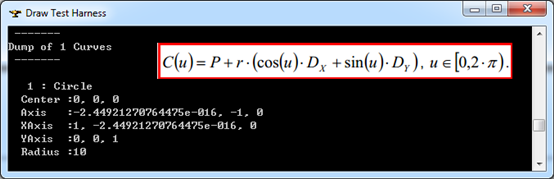
Figure 3.4 Parameters and Parametric equation of the Curve 3D
由上圖可知,三維空間曲線1是一個圓,圓心位于坐標原點(0,0,0),半徑為10,且位于XOZ平面上,對應范圍的起點和終點分別為:
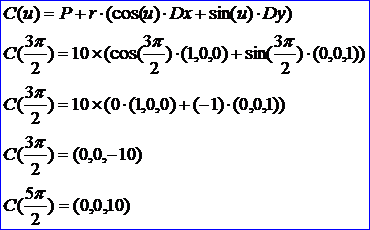
同理根據(jù)曲面上曲線的PCurve的定義,可以計算出曲面1上的曲線2和3,它們表示的曲線與三維空間曲線1相同,即邊#6是銜接邊(Seam Edge),對應OpenCascade中即是BRep_CurveOnClosedSurface。綜上所述,可以畫出球上的Edge,如下圖所示:
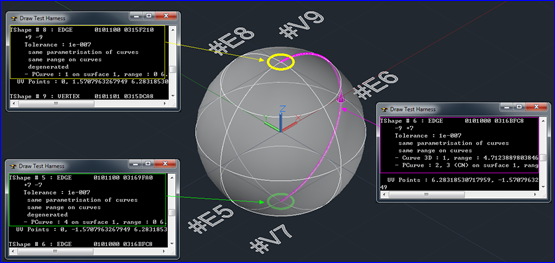
Figure 3.5 Edges of the Sphere
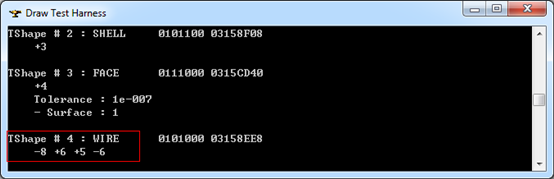
Figure 3.6 Wire of the Sphere
由上圖可知在形成Wire時,Edge6使用了兩次且方向相反,退化邊(Degenerated Edge)的方向可忽略,因為其已經(jīng)退化為一點。根據(jù)Wire的信息畫出球的Wire如下圖所示:
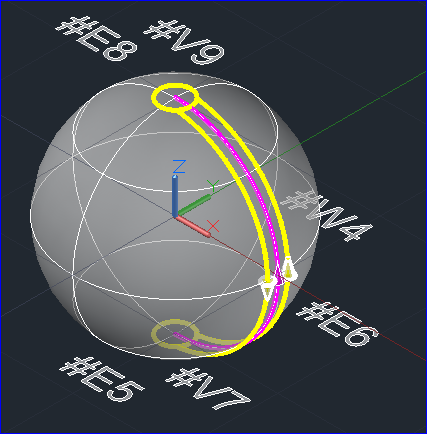
Figure 3.7 Wire of the Sphere(Wire in Yellow color)
由Wire#4組成了Face#3,F(xiàn)ace#3中的幾何曲面為1。曲面1是一個參數(shù)的球面。由Face#3組成Shell #2,由Shell#2組成了Solid#1。球的邊界表示的分析就結(jié)束了。
4. Conclusion
本文通過使用Tcl腳本在Draw Test Harness中生成球的BRep邊界表示信息,分析了球在OpenCascade中的組織方式。對BRep中邊包含的多種幾何曲線形式進行了解。
5. References
1. OpenCascade, Test Harness User’s Guide 2013
2. OpenCascade, BRep Format Description White Paper, 2013
3. John K. Ousterhout, Tcl and Tk Toolkit, 1993