PCurve - Curve on Surface
eryar@163.com
Abstract. 本文通過給出曲面上曲線PCurve的定義來對(duì)OpenCascade中的Curve On Surface進(jìn)行理解,并介紹了OpenCascade對(duì)應(yīng)的類BRep_CurveOnSurface實(shí)現(xiàn)。通過Tcl腳本輸出的球的拓樸信息,分析PCurve的實(shí)際應(yīng)用。
Key words. OpenCascade, ACIS, PCurve, Curve on Surface, Parametric Surface
1. Introduction
不管是ACIS還是OpenCascade中都有PCurve這個(gè)概念,字面上來理解就是參數(shù)曲線(Parametric Curve)。在《基于ACIS的幾何造型技術(shù)與系統(tǒng)開發(fā)》中也看到這個(gè)概念,如下圖所示:
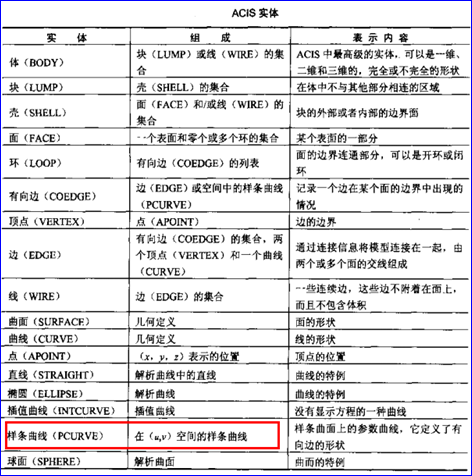
Figure 1.1 PCurve Entity of ACIS
“參數(shù)空間曲線是在參數(shù)曲面的雙參數(shù)空間中的二維樣條曲線。類pcurve是附加在參數(shù)曲面之間公共邊上的數(shù)據(jù)結(jié)構(gòu)。”看完之后,對(duì)pcurve的概念還是不太清楚。本文給出PCurve的定義,并介紹PCurve在OpenCascade中的實(shí)現(xiàn)。根據(jù)定義可以對(duì)PCurve有個(gè)基本認(rèn)識(shí)。
2. Definition of PCurve
PCurve為曲面上的曲線(Curve on Surface),其定義為:設(shè)曲面方程為
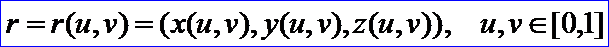 令參數(shù)u,v又是另一參數(shù)t的函數(shù),即
令參數(shù)u,v又是另一參數(shù)t的函數(shù),即
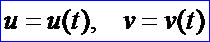
將其代入曲面方程,得到:

當(dāng)t變化時(shí),就得到曲面上的一條單參數(shù)曲線,稱為曲面上的曲線或簡(jiǎn)稱曲面上曲線(Curve on Surface)。若以s表示曲面上曲線的弧長(zhǎng),則由復(fù)合函數(shù)的求導(dǎo)公式可得弧長(zhǎng)微分公式:

令:

則有:
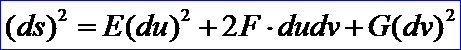
在古典微分幾何中,上式稱為曲面的第一基本公式,E,F(xiàn),G稱為第一基本量。在曲面上,每一點(diǎn)的第一基本量與參數(shù)化無關(guān),在整張曲面上,第一基本量是參數(shù)u和v的連續(xù)函數(shù)。讀者注意,弧元ds是曲線的幾何不變量,與曲面的參數(shù)化無關(guān)。關(guān)于曲線曲面更多的信息,請(qǐng)參考《微分幾何》、《計(jì)算幾何》之類的書籍。本文主要為了理解曲面上曲線PCurve的概念及其在OpenCascade中的實(shí)現(xiàn)。
目前對(duì)PCurve的應(yīng)用還不太清楚,但是微分幾何中引入這個(gè)概念肯定是有他的意義,就像在程序設(shè)計(jì)中引入Pimpl(pointer to implementation)這個(gè)idiom。盡管引入Pimpl idiom會(huì)增加內(nèi)存的額外開銷,甚至因?yàn)樵黾恿碎g接層使程序代碼變得不易讀和不好調(diào)試,但是人們?nèi)匀粯酚谑褂谩U驹贏PI設(shè)計(jì)者的角度,它能隱藏信息、降低耦合、減少文件間的依賴,加快編譯速度、且可使生成的庫的兼容性更好等等,很多優(yōu)點(diǎn)。所以在《Effective C++》和《API Design for C++》中,作者反復(fù)提到并使用Pimpl idiom。類比微分幾何引入的PCurve,先在此做上標(biāo)記,如果有了新的理解再做分析。
3. PCurve in OpenCascade
在OpenCascade中對(duì)應(yīng)于曲面上曲線PCurve的類是BRep_CurveOnSurface,其文檔中的說明為:Representation of a curve by a curve in the parametric space of a surface.
結(jié)合定義上面這句話就好理解了。現(xiàn)摘抄部分代碼來分析PCurve的定義和使用:
//=======================================================================
//function : BRep_CurveOnSurface
//=======================================================================
BRep_CurveOnSurface::BRep_CurveOnSurface(const Handle(Geom2d_Curve)& PC,
const Handle(Geom_Surface)& S,
const TopLoc_Location& L) :
BRep_GCurve(L,PC->FirstParameter(),PC->LastParameter()),
myPCurve(PC),
mySurface(S)
{
}
//=======================================================================
//function : D0
//=======================================================================
void BRep_CurveOnSurface::D0(const Standard_Real U, gp_Pnt& P) const
{
// shoud be D0 NYI
gp_Pnt2d P2d = myPCurve->Value(U);
P = mySurface->Value(P2d.X(),P2d.Y());
P.Transform(myLocation.Transformation());
}
從其構(gòu)造函數(shù)來看,要生成一個(gè)PCurve必須有曲線PC和曲面S及位置L。
從求PCurve的零次微分的函數(shù)D0可以看出,只需要一個(gè)參數(shù)U就可以計(jì)算出曲面上的點(diǎn)P。結(jié)合前面介紹的PCurve的定義,不難理解這段代碼的意義。下面通過分析球面的拓樸結(jié)構(gòu),看看PCurve的應(yīng)用。
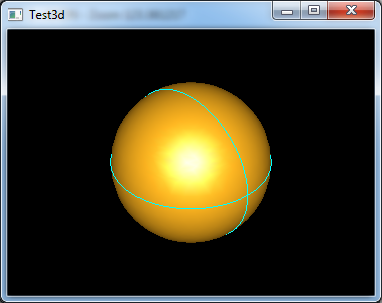
Figure 3.1 Sphere in Draw Test Harness
4. Code Demo
下面的程序生成一個(gè)球,再把其拓樸結(jié)構(gòu)顯示出來,可以看到其中就有PCurve的信息。使用Tcl腳本程序示例如下:
pload ALL
psphere s 1.0
dump s
以上Tcl腳本在OpenCascade的Draw Test Harness中運(yùn)行結(jié)果如下所示:
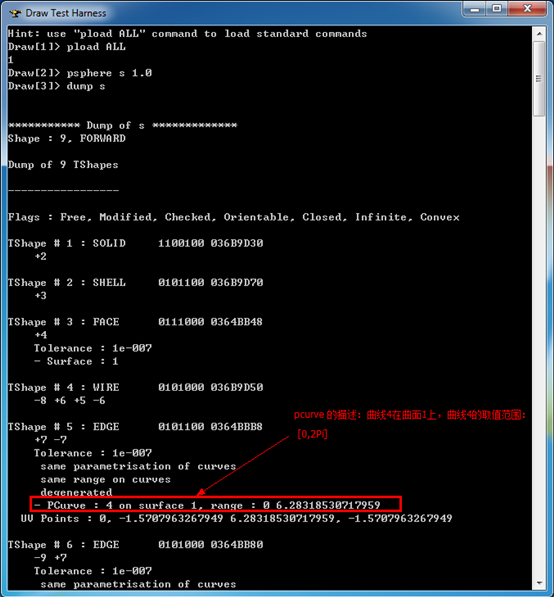
Figure 4.1 PCurve in Sphere
由上圖可知,球的Edge5由一個(gè)PCurve來表示。曲面上曲線PCurve在拓樸結(jié)構(gòu)輸出的信息位于Curve2ds中,曲面的幾何數(shù)據(jù)位于surfaces中,分別如下圖所示:
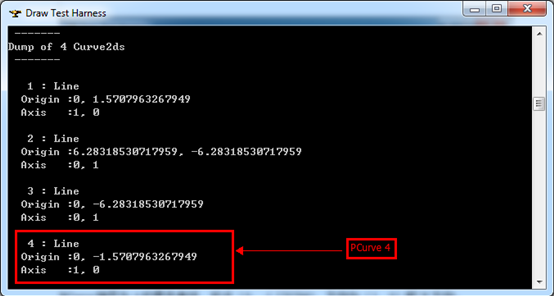
Figure 4.2 PCurves of Sphere
PCurve編號(hào)為4的是條直線,起點(diǎn)(0,-1.570796),方向?yàn)椋?,0)即X方向。
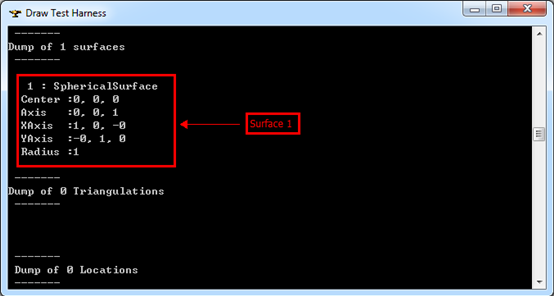
Figure 4.3 Surfaces of Sphere
曲面編號(hào)為1的是一個(gè)球面,圓心(0,0,0),半徑為1,坐標(biāo)系與世界坐標(biāo)系相同。
結(jié)合PCurve 4和曲面1及PCurve的參數(shù)范圍,可以計(jì)算出曲面上的一條曲線上的坐標(biāo)值。不過上面球面的例子中的Edge是degenerated邊,退化成一個(gè)點(diǎn)了。
由上面球的拓樸信息可知,在理解了參數(shù)曲線曲面(有向性)、奇點(diǎn)(Singular Point),參數(shù)曲面的奇異性(Singularity)、曲面上曲線(PCurve)等概念后,OpenCascade的拓樸結(jié)構(gòu)就可以基本理解了。
5. Conclusions
本文通過給出曲面上曲線PCurve的定義來對(duì)OpenCascade中的Curve On Surface進(jìn)行理解,并介紹了OpenCascade對(duì)應(yīng)的類BRep_CurveOnSurface實(shí)現(xiàn)。
通過Tcl腳本輸出的球的拓樸信息,看看PCurve的實(shí)際應(yīng)用,從中可以看出使用Tcl的簡(jiǎn)單與便捷。
6. References
1. 朱心雄,自由曲線曲面造型技術(shù),科學(xué)出版社,2000
2. 王仁宏 李崇君 朱春鋼,計(jì)算幾何教程,科學(xué)出版社,2008
3. 陳維桓,微分幾何,北京大學(xué)出版社,2006
4. 詹海生 李廣鑫 馬志欣,基于ACIS的幾何造型技術(shù)與系統(tǒng)開發(fā),清華大學(xué)出版社,2002