在現(xiàn)實中，面對男生們前仆后繼的表白，MM 們也少不了這樣的糾結(jié)。如果遇到了一個優(yōu)秀的男生，應(yīng)該接受還是拒絕呢？如果接受了他，萬一下一個更好的話那可就虧大了；可如果為此而拒絕掉一個又一個好 男人，也會面對著“過了這個村就沒這個店”的風(fēng)險。說不定白馬王子們都已經(jīng)擦肩而過，到最后就只剩下了猥瑣男了，當(dāng)初的拒絕明顯得不償失。

由于沒人能知道真正的緣分何時到來，沒人能知道下一個來求愛的男生會是什么樣子，接受表白的時機早晚實在很難決定。怎么辦？去向《非誠勿擾》的黃菡 老師和樂嘉老師請教一下？其實你還可以向歐拉老師請教一下。你沒聽錯。大數(shù)學(xué)家歐拉對一個神秘的數(shù)學(xué)常數(shù) e ≈ 2.718 深有研究，這個數(shù)字和“拒人問題”竟然有著直接的聯(lián)系。

“拒人問題”的數(shù)學(xué)模型

為了便于我們分析，讓我們把生活中各種復(fù)雜糾紛的戀愛故事抽象成一個簡單的數(shù)學(xué)過程。假設(shè)根據(jù)過去的經(jīng)驗，MM 可以確定出今后將會遇到的男生個數(shù)，比如說 15 個、30 個或者 50 個。不妨把男生的總?cè)藬?shù)設(shè)為 n。這 n 個男生將會以一個隨機的順序排著隊依次前來表白。每次被表白后，MM 都只有兩種選擇：接受這個男生，結(jié)束這場“征婚游戲”，和他永遠幸福地生活在一起；或者拒絕這個男生，繼續(xù)考慮下一個表白者。我們不考慮 MM 腳踏兩只船的情況，也不考慮和被拒男生破鏡重圓的可能。最后，男人有好有壞，我們不妨假設(shè) MM 心里會給男生們的優(yōu)劣排出個名次來。

聰明的 MM 會想到一個好辦法：先和前面幾個男生玩玩，試試水深；大致摸清了男生們的底細后，再開始認(rèn)真考慮，和第一個比之前所有人都要好的男生發(fā)展關(guān)系。從數(shù)學(xué)模型 上說，就是先拒掉前面 k 個人，不管這些人有多好；然后從第 k+1 個人開始，一旦看到比之前所有人都要好的人，就毫不猶豫地選擇他。不難看出，k 的取值很講究，太小了達不到試的效果，太大了又會導(dǎo)致真正可選的余地不多了。這就變成了一個純數(shù)學(xué)問題：在男生總數(shù) n 已知的情況下，當(dāng) k 等于何值時，按上述策略選中最佳男生的概率最大？

如何求出最優(yōu)的 k 值？

對于某個固定的 k，如果最適合的人出現(xiàn)在了第 i 個位置（k < i ≤ n），要想讓他有幸正好被 MM 選中，就必須得滿足前 i-1 個人中的最好的人在前 k 個人里，這有 k/(i-1) 的可能。考慮所有可能的 i，我們便得到了試探前 k 個男生之后能選中最佳男生的總概率 P(k)：

用 x 來表示 k/n 的值，并且假設(shè) n 充分大，則上述公式可以寫成：

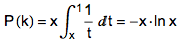
對 -x · ln x 求導(dǎo)，并令這個導(dǎo)數(shù)為 0，可以解出 x 的最優(yōu)值，它就是歐拉研究的神秘常數(shù)的倒數(shù)—— 1/e ！

也就是說，如果你預(yù)計求愛者有 n 個人，你應(yīng)該先拒絕掉前 n/e 個人，靜候下一個比這些人都好的人。假設(shè) 你一共會遇到大概 30 個求愛者，就應(yīng)該拒絕掉前 30/e ≈ 30/2.718 ≈ 11 個求愛者，然后從第 12 個求愛者開始，一旦發(fā)現(xiàn)比前面 11 個求愛者都好的人，就果斷接受他。由于 1/e 大約等于 37%，因此這條愛情大法也叫做 37% 法則。

不過，37% 法則有一個小問題：如果最佳人選本來就在這 37% 的人里面，錯過這 37% 的人之后，她就再也碰不上更好的了。但在游戲過程中，她并不知道最佳人選已經(jīng)被拒，因此她會一直癡癡地等待。也就是說，MM 將會有 37% 的概率“失敗退場”，或者以被迫選擇最后一名求愛者的結(jié)局而告終。

37% 法則“實測”！

37% 法則的效果究竟如何呢？我們在計算機上編寫程序模擬了當(dāng) n = 30 時利用 37% 法則進行選擇的過程（如果 MM 始終未接受求愛者，則自動選擇最后一名求愛者）。編號越小的男生越次，編號為 30 的男生則表示最佳選擇。程序運行 10000 次之后，竟然有大約 4000 次選中最佳男生，可見 37% 法則確實有效啊。

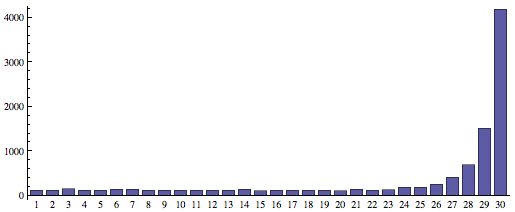
計算機模擬 10000 次后得到的結(jié)果

這個問題由數(shù)學(xué)家 Merrill M. Flood 在 1949 首次提出，這個問題被他取名為“未婚妻問題”。這個問題的精妙之處在于，在微積分界叱咤風(fēng)云的自然底數(shù) e，竟也出人意料地出現(xiàn)在了這個看似與它毫不相關(guān)的問題中。不知道此問題發(fā)表后，Geek 男女間會不會多了一種分手的理由：不好意思，你是那 37% 的人⋯⋯