Let it Bead,POJ 2409
Let it Bead
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 2318 | Accepted: 1448 |
Description
"Let
it Bead" company is located upstairs at 700 Cannery Row in Monterey,
CA. As you can deduce from the company name, their business is beads.
Their PR department found out that customers are interested in buying
colored bracelets. However, over 90 percent of the target audience
insists that the bracelets be unique. (Just imagine what happened if two
women showed up at the same party wearing identical bracelets!) It's a
good thing that bracelets can have different lengths and need not be
made of beads of one color. Help the boss estimating maximum profit by
calculating how many different bracelets can be produced.
A bracelet is a ring-like sequence of s beads each of which can have one of c distinct colors. The ring is closed, i.e. has no beginning or end, and has no direction. Assume an unlimited supply of beads of each color. For different values of s and c, calculate the number of different bracelets that can be made.
A bracelet is a ring-like sequence of s beads each of which can have one of c distinct colors. The ring is closed, i.e. has no beginning or end, and has no direction. Assume an unlimited supply of beads of each color. For different values of s and c, calculate the number of different bracelets that can be made.
Input
Every
line of the input file defines a test case and contains two integers:
the number of available colors c followed by the length of the bracelets
s. Input is terminated by c=s=0. Otherwise, both are positive, and, due
to technical difficulties in the bracelet-fabrication-machine,
cs<=32, i.e. their product does not exceed 32.
Output
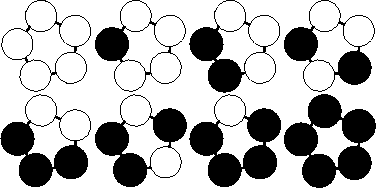 For
each test case output on a single line the number of unique bracelets.
The figure below shows the 8 different bracelets that can be made with 2
colors and 5 beads.
For
each test case output on a single line the number of unique bracelets.
The figure below shows the 8 different bracelets that can be made with 2
colors and 5 beads.Sample Input
1 1
2 1
2 2
5 1
2 5
2 6
6 2
0 0
Sample Output
1
2
3
5
8
13
21
Source
Ulm Local 2000
赤裸裸的 Polya,旋轉 i 的循環個數為 gcd( i, n )
1 #include <iostream>
2
3 using namespace std;
4
5 typedef long long Lint;
6
7 Lint gcd( Lint a, Lint b ) {
8 return ( (b==0) ? a : gcd(b,a%b) );
9 }
10
11 Lint power( Lint a, Lint b ) {
12 Lint ans = 1;
13 while ( b-- > 0 ) {
14 ans *= a;
15 }
16 return ans;
17 }
18
19 Lint solve( Lint n, Lint m ) {
20 Lint i, ans = 0;
21 for ( i = 1; i <= n; ++i ) {
22 ans += power( m, gcd(n,i) );
23 }
24 if ( n & 1 ) {
25 ans += n * power( m, n/2+1 );
26 }
27 else {
28 ans += power( m, n/2 ) * n / 2 + power( m, n/2+1 ) * n / 2;
29 }
30 ans /= n + n;
31 return ans;
32 }
33
34 int main() {
35 Lint n, m;
36 for ( ; ; ) {
37 cin >> m >> n;
38 if ( (m<1) && (n<1) ) {
39 break;
40 }
41 cout << solve( n, m ) << "\n";
42 }
43 return 0;
44 }
45
2
3 using namespace std;
4
5 typedef long long Lint;
6
7 Lint gcd( Lint a, Lint b ) {
8 return ( (b==0) ? a : gcd(b,a%b) );
9 }
10
11 Lint power( Lint a, Lint b ) {
12 Lint ans = 1;
13 while ( b-- > 0 ) {
14 ans *= a;
15 }
16 return ans;
17 }
18
19 Lint solve( Lint n, Lint m ) {
20 Lint i, ans = 0;
21 for ( i = 1; i <= n; ++i ) {
22 ans += power( m, gcd(n,i) );
23 }
24 if ( n & 1 ) {
25 ans += n * power( m, n/2+1 );
26 }
27 else {
28 ans += power( m, n/2 ) * n / 2 + power( m, n/2+1 ) * n / 2;
29 }
30 ans /= n + n;
31 return ans;
32 }
33
34 int main() {
35 Lint n, m;
36 for ( ; ; ) {
37 cin >> m >> n;
38 if ( (m<1) && (n<1) ) {
39 break;
40 }
41 cout << solve( n, m ) << "\n";
42 }
43 return 0;
44 }
45
posted on 2011-04-17 22:11 coreBugZJ 閱讀(445) 評論(0) 編輯 收藏 引用 所屬分類: ACM