OpenCASCADE 線面求交

eryar@163.com

1 Introduction

OpenCASCADE中幾何曲線與曲面求交使用類GeomAPI_IntCS，是對類IntCurveSurface_HInter的簡單封裝。在IntCurveSurface_HInter中對曲線和曲面求交分為以下幾種類型：

• PerformConicSurf：二次曲線與曲面求交，其中又分為兩類：二次曲線與二次曲面求交和二次曲線和自由曲面求交；
• InternalPerformCurveQuadric：自由曲線與二次曲面求交；
• InternalPerform：自由曲線和自由曲面求交；

本文主要介紹曲線與曲面求交的實現原理。

2 二次曲線與二次曲面求交

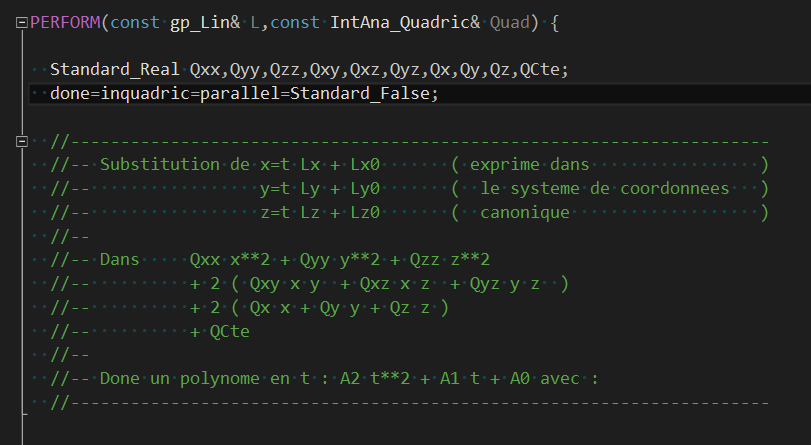
二次曲線與二次曲面求交使用IntAna_ConicQuad計算，主要思路是將曲線用參數方程表示，代入二次曲面的代數方程。二次曲面可以使用二次多項式表示，將二次曲線與二次曲面相交表示成一個多項式方程，使用math_DirectPolynomialRoots對多項式方程進行求解。

3 二次曲線與自由曲面求交

二次曲線與自由曲面求交將曲面使用IntCurveSurface_Polyhedron在U，V上采樣離散得到grid網格。這個類實現與IntPolyh_MaillageAffinage類功能有重復。

IntCurveSurface_ThePolygon多段線與Intf_InterferencePolygonPolyhedron 網格求交，根據多段線與網格求交情況，找到初始值，使用IntImp_IntCS計算精確值。與曲面求交的Marching算法類似，使用迭代法去計算精確交點。迭代方程為IntImp_ZerCSParFunc，寫出這個方程的Value()值計算和Derivatives()微分計算公式。

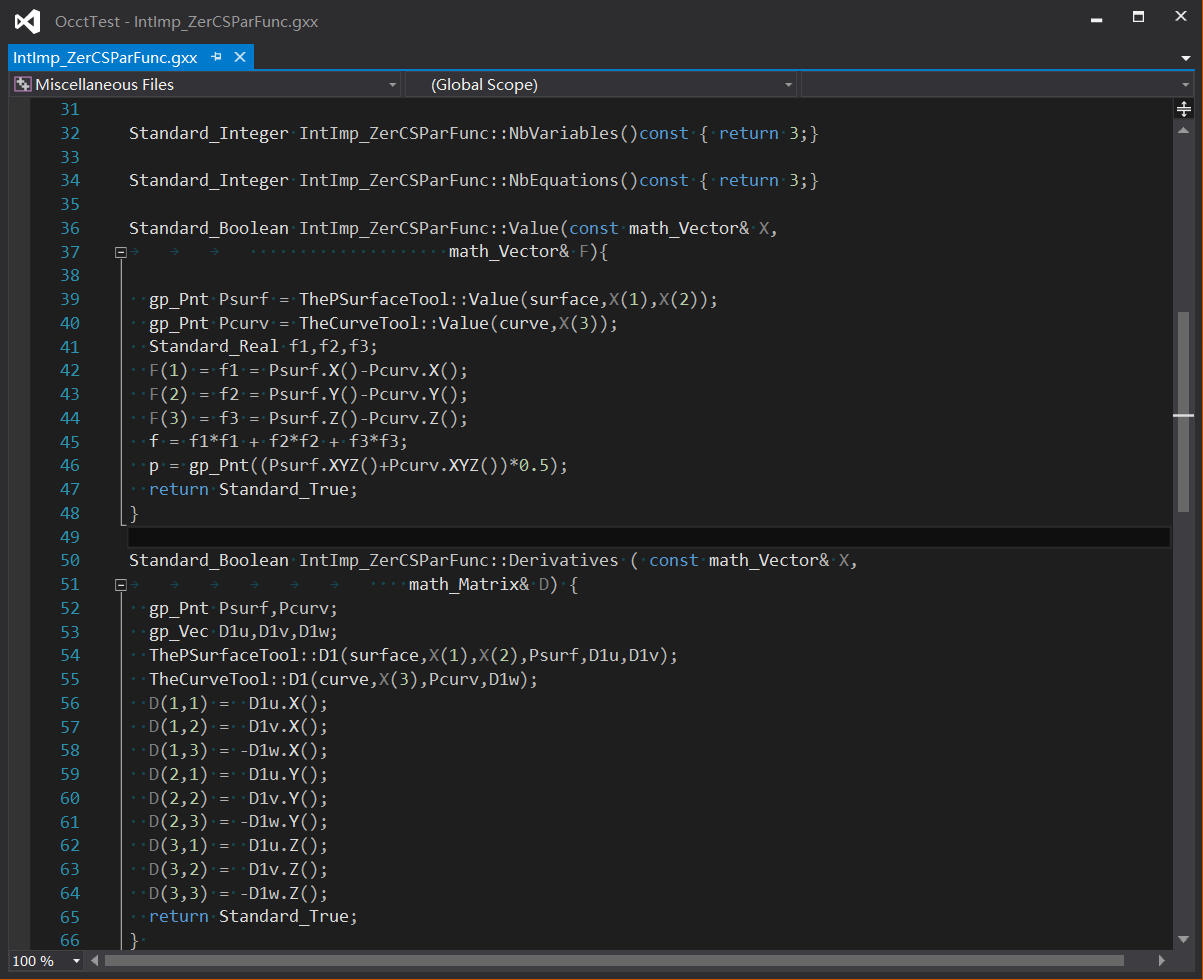
將曲線與曲面求交問題轉化為求曲面參數u,v和曲線參數w，使曲線C(w)曲面S(u,v)上的點重合，建立函數如下：

F(u,v,w)=S(u,v) - C(w)

所求的精確交點滿足方程F(u,v,w)=0，F為一含有三個坐標的矢量，對應函數Value()：

Fx(u,v,w)=Sx(u,v) - Cx(w) = 0

Fy(u,v,w)=Sy(u,v) - Cy(w) = 0

Fz(u,v,w)=Sz(u,v) - Cz(w) = 0

上面為含有三個方程的以u,v,w為變量的非線性方程組，精確交點就是非線性方程組的解。使用類math_FunctionSetRoot應用Newton-Raphson迭代法求解非線性方程組的解。使用Newton迭代法有個前提條件是要求非線性方程組一階可導，即要寫出Jacobian迭代矩陣，即上述函數Derivatives()的實現原理：

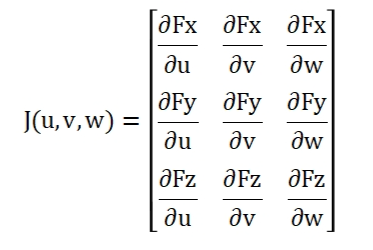
4 自由曲線與二次曲面求交

自由曲線與二次曲面求交IntCurveSurface_TheQuadCurvExactInter ，通過類IntCurveSurface_TheQuadCurvFuncOfTheQuadCurvExactHInter建立二次曲面與曲線之間的函數，是求解曲線上參數U的一元函數。

5 自由曲線與自由曲面求交

自由曲線與自由曲面求交和二維自由曲線求交類似，采用的離散法。即將曲線通過采樣離散成多段線Polygon，將曲面采樣生成網格Polyhedron，通過類IntCurveSurface_TheInterferenceOfHInter來計算多段線與網格的相交。

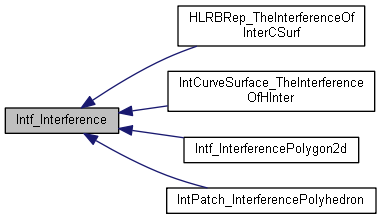
包Intf主要用來計算二維多段線、三維多段線及網格的相交。根據離散計算的粗交點，再根據類IntCurveSurface_TheExactHInter使用迭代法求得精確交點。這個思想與曲面和曲面求交相同。

6 求交結果

曲線與曲面求交的結果主要也是保存在類IntCurveSurface_Intersection對象中，這個類的設計與二維曲線求交類似，不夠直接。

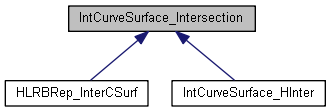
可以看到IntCurveSurface_Intersection這個類的構造函數是protected的，意思是不能直接使用，通過派生類IntCurveSurface_HInter調用SetValues()函數將求交結果保存起來。求交結果為交點IntCurveSurface_IntersectionPoint和交線IntCurveSurface_IntersectionSegment。

其中交點中IntCurveSurface_IntersectionPoint保存了三維坐標點，交點在曲面上的U,V參數，交點在曲線上的參數U及相交狀態。交線主要是線現面和重合部分的幾何奇異情況數據。

從類圖上可以看出，這個套路同樣用到了HLR算法中，理解這個套路對理解HLR算法有幫助。

7 Conclusion

綜上所述，OpenCASCADE中將曲線與曲面求交根據曲線和曲面類型的不同分別處理。二次曲線曲面求交依賴IntAna包，自由曲線和自由曲面求交使用離散法，最終實現算法與兩個曲面求交的Marching算法類似，通過離散得到的精交點，再代入迭代方程求得精確解。其中把曲線或曲面離散的采樣點沒有考慮曲線或曲面的曲率等，采樣點數量較大，會影響性能 。曲面采樣離散代碼與曲面求交中的有重復。從幾何求交類中可以看到沒有容差的輸入，可以思考一下這個問題。

TKGeomAlgo中除了擬合算法外，大部分代碼主要就是線線求交、線面求交及面面求交算法。理解這些算法的實現原理，為Boolean算法的求交邏輯打下基礎。