幾何內核與數學

1 概述

從1950年第一臺圖形顯示器（美國麻省理工大學MIT旋風I號Whirlwind I）的誕生，到1962年MIT林肯實驗室的Ivan E. Sutherland發表題為“Sketchpad: 一個人機交互的圖形系統”確定計算機圖形學作為獨立科學分支。經過70多年的發展，計算機圖形學中的幾何造型技術成了現在的幾何內核。

數學是我們從小學、中學到大學一直都在學習的課程，是現代科技的理論基礎，是創新的源泉。幾何內核與數學的聯系非常緊密，結合開源幾何內核opencascade談談學習過程和數學的認識。

2 高中時代

在剛學習的時候，總是先從簡單的開始入手。比如，先看看直線、圓是什么，怎么顯示出來。長方體、圓柱體等怎么用BREP進行表示，怎么顯示在屏幕上。這個時候考慮問題是常人思維，我認為是高中時代。

比如，怎么計算二維直線與圓的交點呢？上過高中的都學過，聯立直線與圓的一元二次方程組，將解方程組的代碼固化在代碼中。當計算橢圓與圓的交點時，也做同樣的處理，就是多寫點代碼。高中幾何學得好的，可能會說我可以用向量，向量的方法會比代數的方法速度要快。

再比如，怎么計算曲線的弧長和曲面的面積呢？計算曲線可以通過對曲線進行采樣點，將點連成多段線，再分別計算每小段線段的長度累加就是了。面積咱們也可以類似處理，將曲面離散成三角形或四邊形，再將這些三角形或四邊形面積累加。這些方法都能實現，但是性能、精度都會成為問題。要計算得精度高，采樣就要密，就會帶來性能問題。

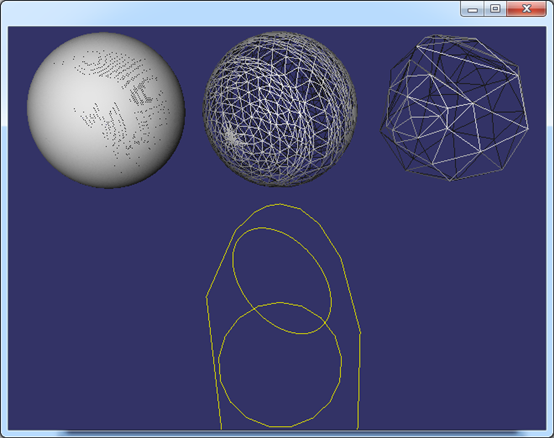
3 大學時代

到了大學時代學習過高等數學、線性代數等，有了更有力的工具來解決更一般問題。面向對象編程和數學也是相通的，就是將問題抽象的能力。這個時候眼中沒有直線、圓、B樣條曲線、平面、球面、B樣條曲面等等，只有線Curve和面Surface。

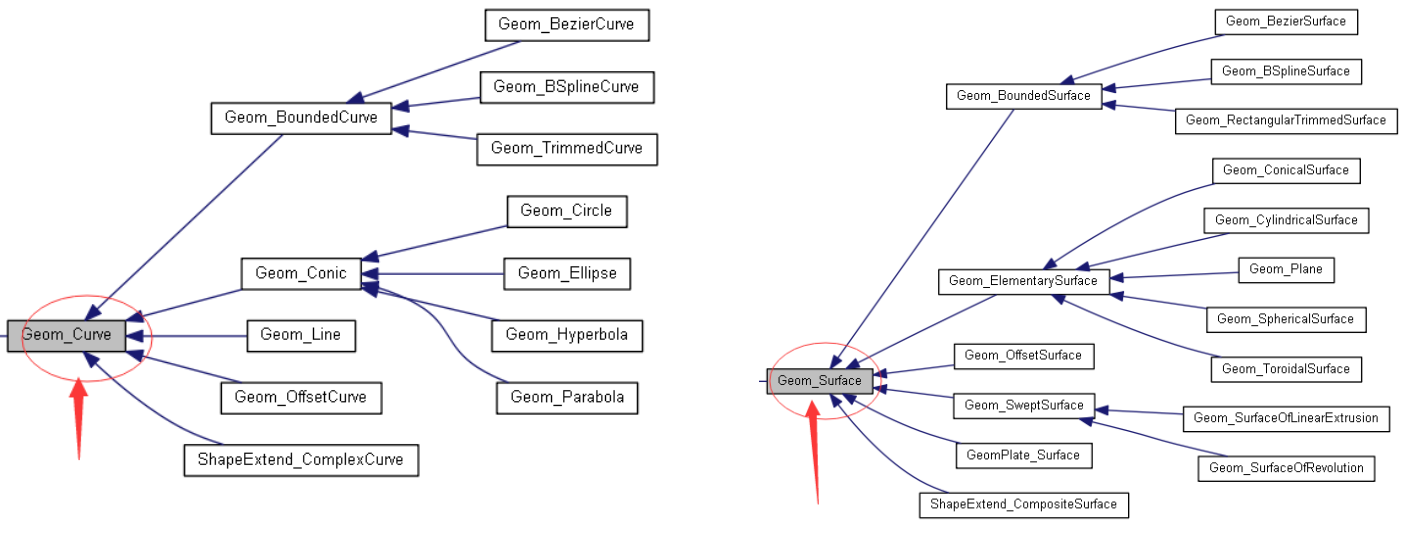
再進一步抽象，將線Curve與一元函數F(x)對應，將面Surface與多元函數對應F(x,y)，與數學建立了聯系。

這時就可以使用數學工具對問題進行處理了。如計算曲線弧長，就變成一個對切向量的積分。曲線切向量需要計算一階導數，《The NURBS Book》等書上計算B樣條微分的公式就有用，看待B樣條曲線和看待圓一樣了。

積分的計算可以使用數值方法，如Newton-Cotes或Gauss積分法，使用更少的迭代獲得更高的精度，程序優化的方向也清晰。

從opencascade的類math_Function和math_MultipleVarFunction可以可以看出，許多幾何問題都抽象成了數學問題。有很多人問我，怎樣才算入門了opencascade呢？那就是思考問題的方式轉換成數學的方式，我覺得就算入門了。再具體點可操作點呢，首先就是數據結構的入門，掌握BREP邊界表示法，如在圓柱面Surface上框出一個小面片Face，能正常顯示出來就算理解opencascade中的BREP結構。其次是幾何算法入門，就是將從math_Function和math_MultipleVarFunction所有的派生類的數學公式寫出來。這兩點動手做完，我覺得可以算入門了。

4 研究生時代

如果大學時代我們掌握了微分、積分、線性代數，到研究生時代應該掌握變分、偏微分方程、最優化理論等等。如偏微分方程用于構造過渡曲面，曲線曲面擬合光順最后都抽象成帶約束的非線性方程組的求解。

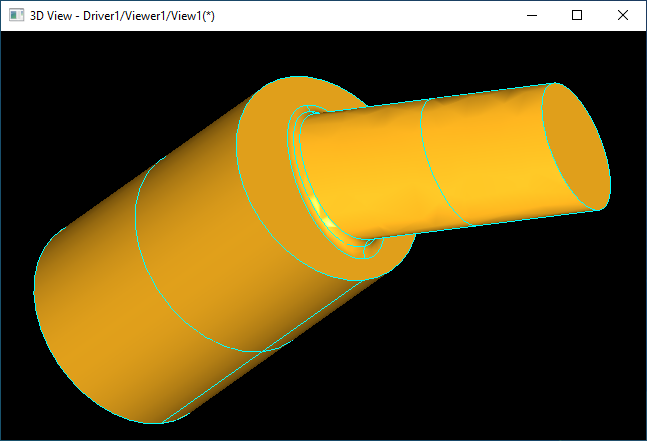
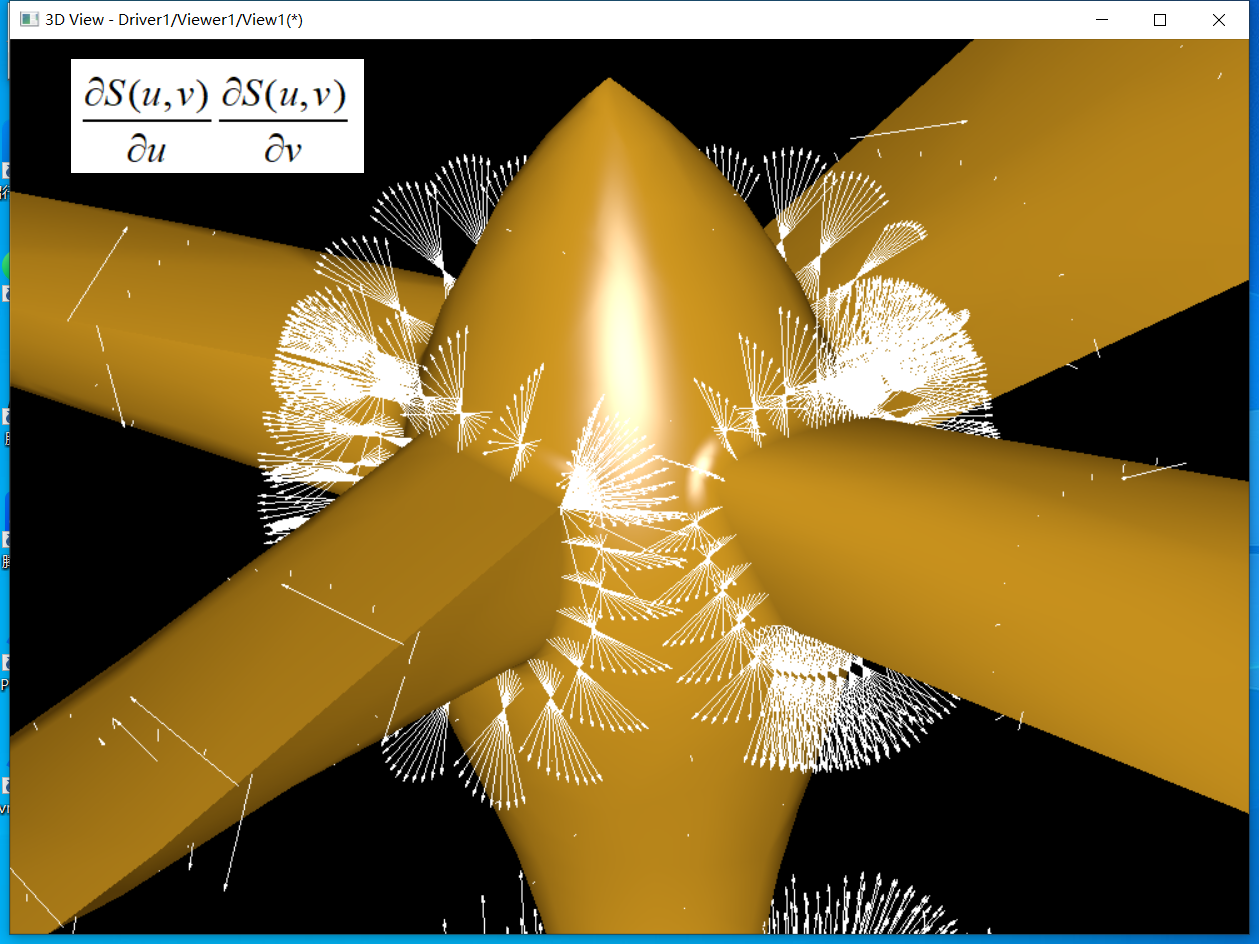
到研究生時代因為掌握的數學工具，會處理看上去很簡單但處理起來更復雜的問題：如上圖所示的過渡Blend，以及蒙面Skinning和掃掠Sweep等。

這時也可以有一些智能算法，如遺傳算法、蟻群，粒子群PSO優化算法，AI等，使用仿生、遺傳變異等手段使求解迭代更快收斂。為傳統優化算法提供初始解，使傳統算法能更快、更準地找到解析解，不至于深陷局部最優解中不能自拔。在opencascade中也有相關實例，如math_PSO。這些智能算法有隨機性，不像解析算法那樣滿足一定約束條件必定會找到相對準確答案。只能作為像曲面求交之網格離散法，作為參數迭代法的預處理。到這個時代，查看相關技術論文毫無壓力，面對一般的幾何問題都應該可以從容應對。和研究生一樣面對的問題更加具體，會鉆牛角尖。

5 總結

綜上所述，幾何內核可以看成一個數學庫的子集，只是在幾何圖形上的應用。學習幾何內核的過程類比于學生時代掌握的數學工具。在高中時代，看問題很具體，只能case by case的處理，功能能做出來。到大學時代，有了一定的抽象能力（與面向對象編程一樣），看問題具有一般性，能使用更高級點的數學工具來處理，有能力來兼顧精度和性能。到了研究生時代，就不怕別人來卡脖子，甚至能超越別人。這個時候不要給自己設限，找準喜歡的方向去鉆牛角尖，終會有所成。