OpenCASCADE曲面交線分類
eryar@163.com
Abstract. OpenCascade classify the intersection line between two surfaces. A intersection line may be either geometric: line, circle, ellipse, parabola, hyperbola as defined in the class GLine, or analytic as defined in the class ALine, or defined by a set of points(coming from a walking algorithm) as defined in the class WLine. Or described by a restriction line on one of the surfaces as RLine.
Key Words. Surface Intersection, Intersection Line
1 Introduction
OpenCASCADE中對兩個曲面求交得到的交線進行了分類,如下類圖所示:
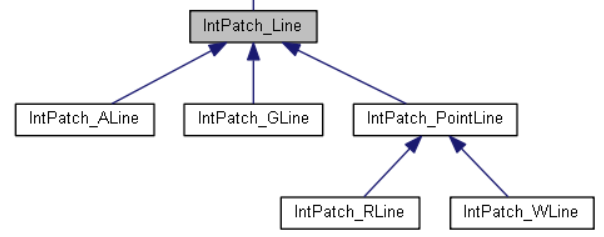
交線總共分為四類:
- ALine:Analytic解析曲線,主要為兩個二次曲面求交所得,如圓柱面、球面、圓錐面等之間的交線;
- GLine:Geometric幾何曲線,即交線可以表示成簡單的二次曲線,如直線、圓、拋物線等;
- WLine:Walking追蹤法得到的交線,保存了追蹤路線上的兩個曲面的交點;
- RLine:Restriction受限交線,這條交線可能只在一個面上;
下面我們使用Tcl腳本在DRAW中驗證一下這四類交線的來源,加深對曲面求交算法的理解。分類帶來了麻煩,可以帶著問題:為什么要分這幾種類型?有什么好處?來看這篇文章。要用好開源的東西,其實要求還是很高的,需要對源碼有相對深入的理解。
2 ALine
Analytic交線是二次曲面求交所得,二次曲面是因為可以統(tǒng)一使用二次型來表示的解析曲面,也是《解析幾何》中研究的主要內(nèi)容。我們可以在DRAW中構(gòu)造圓柱面與圓錐面求交驗證一下。TCL腳本如下:
# Test for IntPatch_ALine.
# Geometry surfaces.
cylinder s1 0 0 0 1 1 1 2
cone s2 0 0 0 0 0 1 1 0 0 30 3
# Topology faces
mkface f1 s1 0 2*pi -8 8
mkface f2 s2 0 2*pi -5 5
# Intersection.
bop f1 f2
bopsection r
# Display result.
vdisplay f1 f2 r
生成結(jié)果如下圖所示,其中紅色為交線:
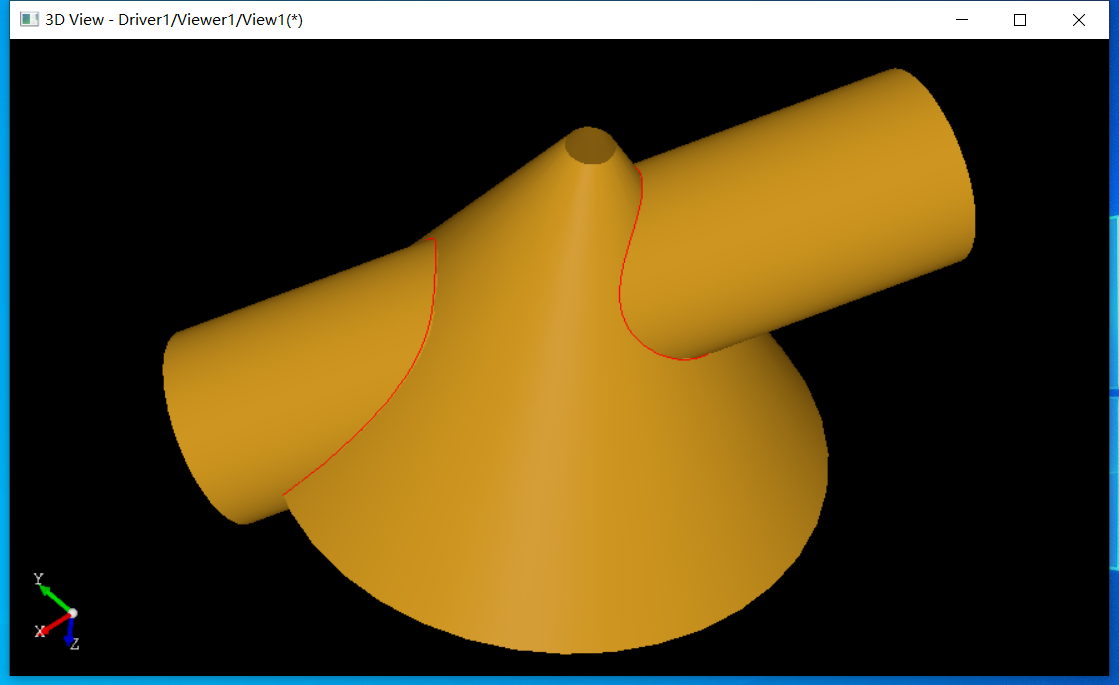
DEBUG源碼可以看到是使用類IntPatch_ImpImpIntersection 計算求交,即兩個解析曲面求交算法類。

3 GLine
Geometric幾何曲線形式簡單,如果交線用幾何曲線來表示,對于后續(xù)算法有好處。如平面與圓錐面求交線,圓柱面與圓柱面求交等,都會得到幾何曲線。將上面的圓柱面換成平面與圓錐面求交我們可以在DRAW驗證經(jīng)典的圓錐與平面交線:根據(jù)平面位置不同,可以得到圓、橢圓、雙曲線等幾何曲線。TCL腳本如下所示:
# Test for IntPatch_GLine.
cone s1 0 0 0 0 0 1 30 3
plane s2 0 0 0 0 0 1
mkface f1 s1 0 2*pi -5 5
mkface f2 s2 -8 8 -8 8
bop f1 f2
bopsection r
vdisplay f1 f2 r
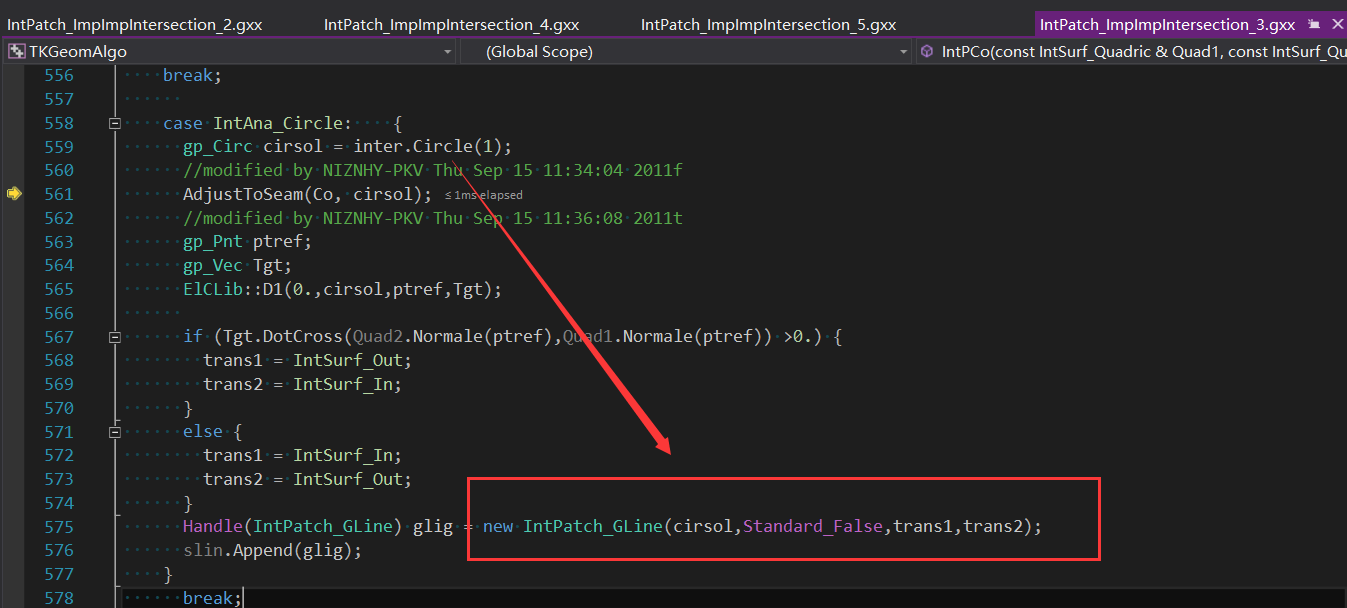
計算交線結(jié)果如下圖所示:

我們改變平面的法向,使其斜著與圓錐面求交,會得到橢圓:
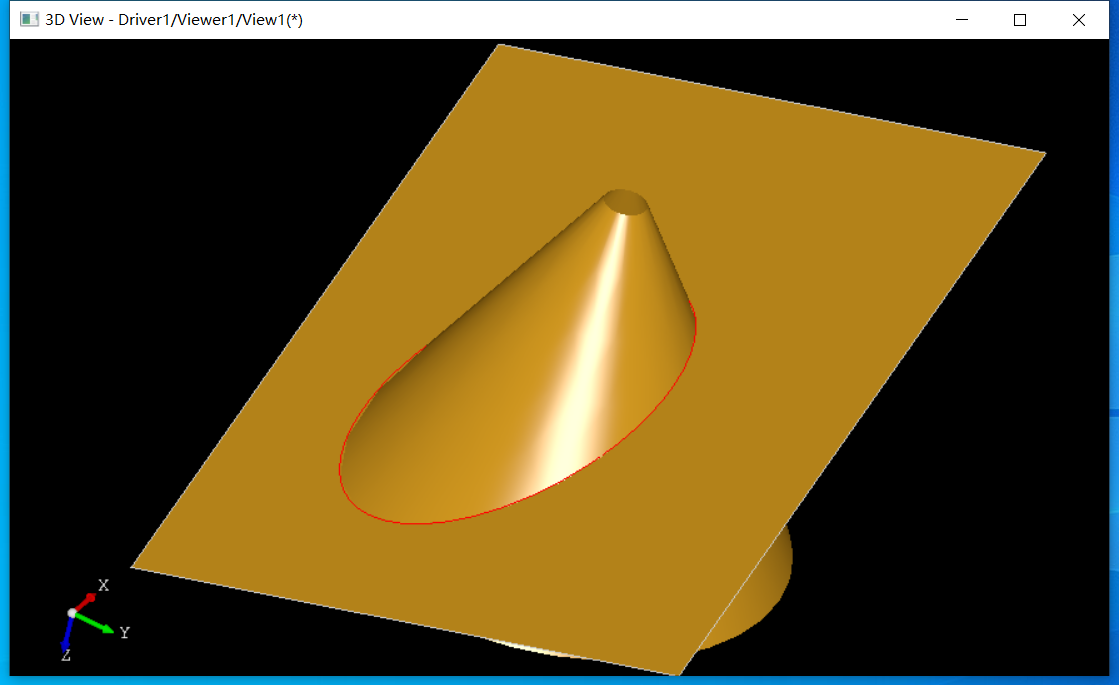
還可以得到雙曲線、拋物線等,同學(xué)們可以自己嘗試一下。
4 WLine
對于NURBS曲面求交,一般會使用Marching方法,國內(nèi)教材翻譯為追蹤法。在看《地球脈動》時,注意到對于大草原上的水牛、大象等動物成群結(jié)隊的遷徙使用了這個詞,這個詞的字面意思有行進、行軍,列隊行進之意,如果結(jié)合opencascade中的walking感覺翻譯為行進法更貼切,因為在opencascade中對于求交專門有個package名為IntWalk,其中類IntWalk_PWalking來使用marching method對兩個參數(shù)曲面進行求交。Walk有行走之意,所以對于使用Walk方法得到的交線命名為WLine。對于NURBS曲面求交及二次曲面與NURBS曲面求交,使用了Marching方法,WLine的來源是清晰的。繼續(xù)使用上面的腳本,只需要將上述兩個面轉(zhuǎn)換成NURBS曲面即可觸發(fā)Marching法進行求交。TCL腳本如下:
# Test for IntPatch_WLine.
cone s1 0 0 0 0 0 1 30 3
plane s2 0 0 0 1 1 2
mkface f1 s1 0 2*pi -5 5
mkface f2 s2 -8 8 -8 8
nurbsconvert f1 f1
nurbsconvert f2 f2
bop f1 f2
bopsection r
vdisplay f1 f2 r
通過IntWalk_PWalking行進法配合三參數(shù)迭代法,將行進過程中的交點都保存在WLine中。
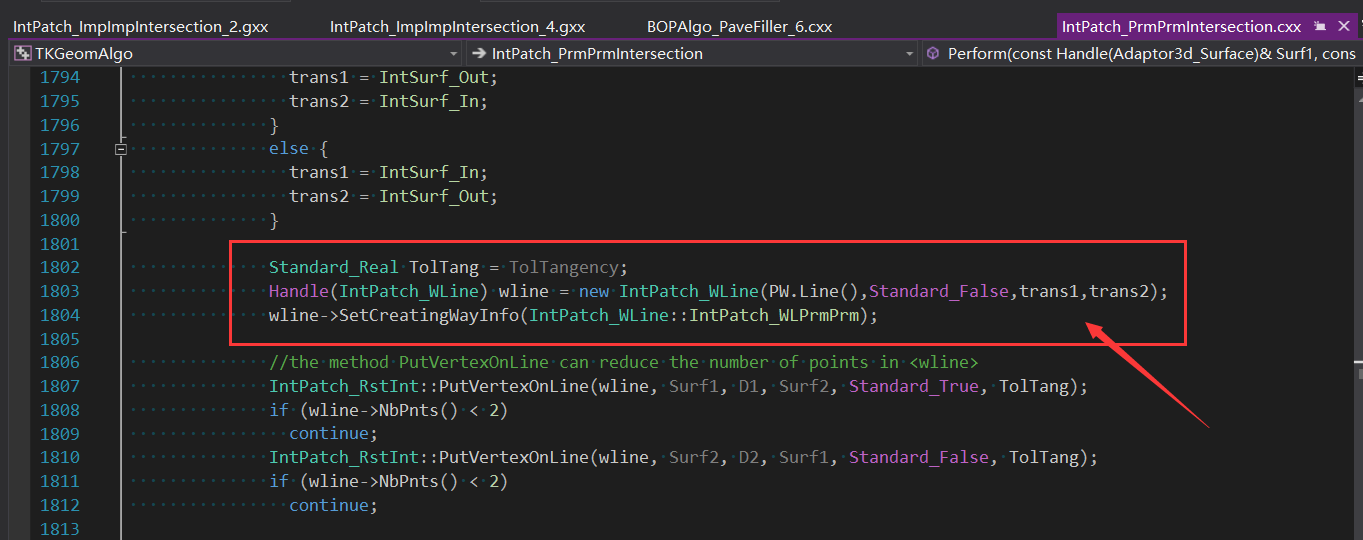
雖然結(jié)果與上面看上去一樣,內(nèi)部交線已經(jīng)不是簡單的幾何曲線了。
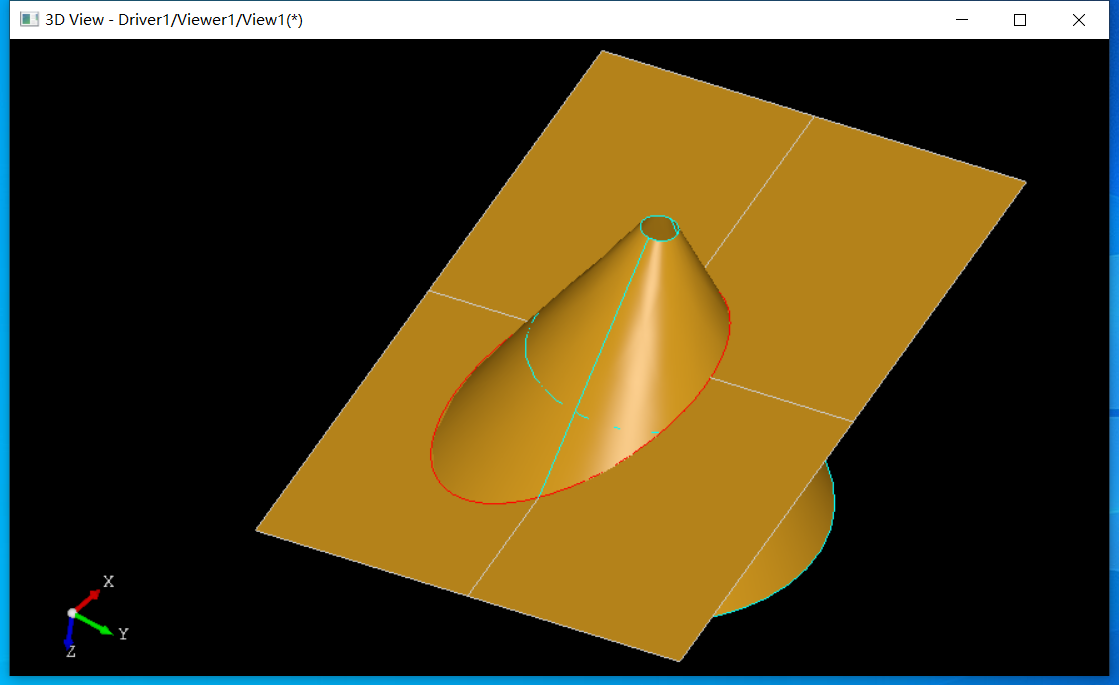
5 RLine
Restriction交線是受限交線,這種類型的交線只會位于一個面上。這里我們構(gòu)造一個平面及與平面重疊的一個NURBS曲面來求交進行解釋。TCL腳本如下:
# Test for IntPatch_RLine.
plane s1 0 0 0 0 0 1
plane s2 0 0 0 0 0 1
mkface f1 s1 -5 5 -5 5
mkface f2 s2 -8 8 -8 8
nurbsconvert f1 f1
bop f1 f2
bopsection r
vdisplay f1 f2 r
DEBUG會發(fā)現(xiàn)這兩個曲面的交線為RLine,并在生成RLine時指定交線屬于哪個曲面,是在S1曲面SetArcOnS1還是在S2曲面SetArcOnS2:
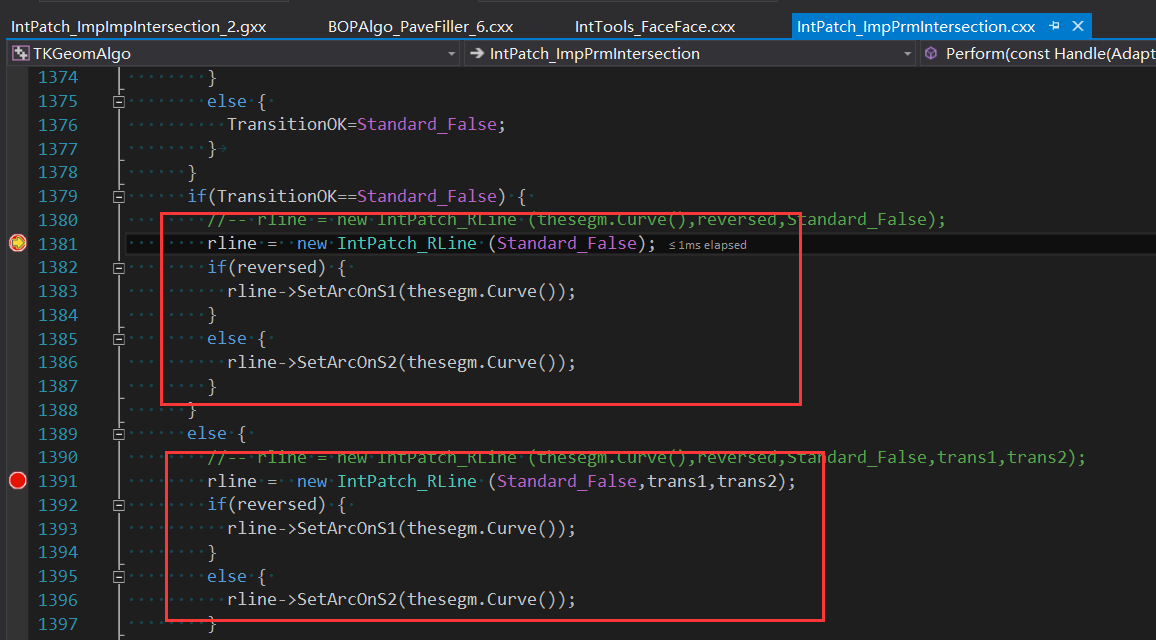
生成交線如下圖所示:
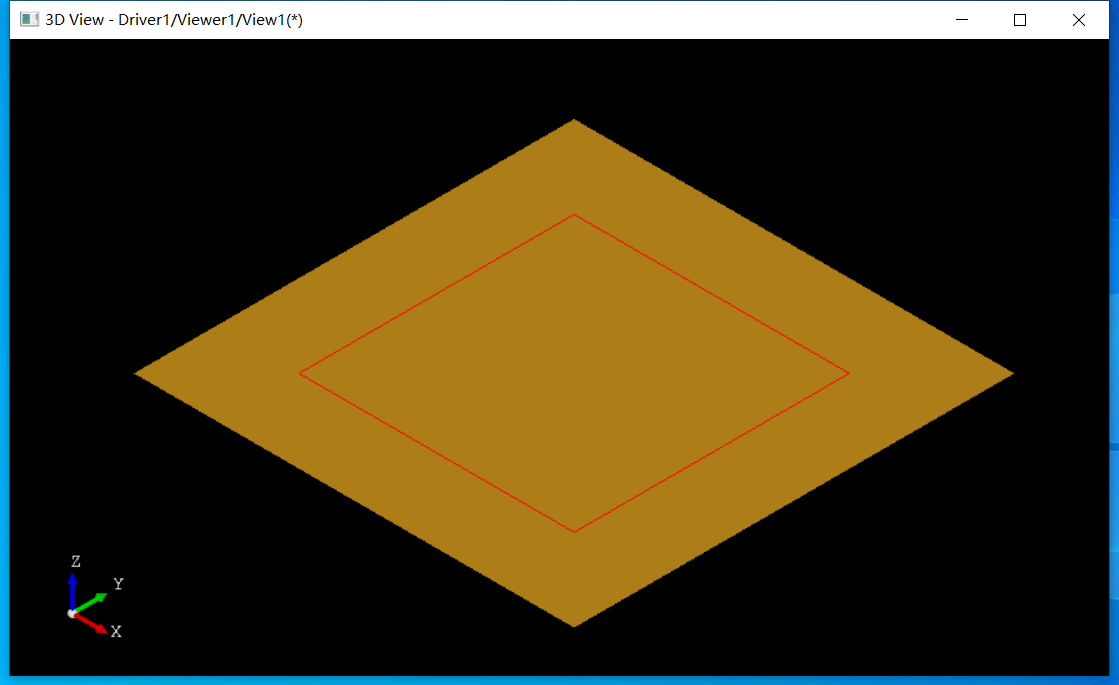
當然可以使用RLine來判斷兩個曲面是否有重疊,但是在opencascade中兩個曲面重疊叫Tangent Face,可以將上述NURBS面不轉(zhuǎn)換,還是使用兩個重疊平面來驗證:

求交最后對交線數(shù)據(jù)歸并時的代碼有點不敢恭維:
6 Conclusion
綜上所述,對兩個曲面求交得到的交線進行分類,避免交線都是NURBS曲線,可以是簡單的二次曲線,提高后續(xù)算法性能。在理解源碼的基礎(chǔ)上,可以根據(jù)實際應(yīng)用場景選擇高效的算法。如若只是求兩個模型之間的交線,可以直接使用曲面求交算法,一般情況下性能還是不錯的。當然理解源碼后,可以結(jié)合實際應(yīng)用場景可以對求交算法做進一步優(yōu)化。
要深入理解opencascade源碼,熟練使用DRAW是一個相對容易的路線。因為在DRAW中可以使用Tcl腳本快速驗證各種想法,甚至直接DEBUG源碼,從表向深入到與源碼作者直接對話。