OpenCASCADE曲面求交之迭代法

eryar@163.com

1 Introduction

朱心雄等著《自由曲線曲面造型技術(shù)》書中對(duì)曲面求交的迭代法有詳細(xì)介紹，其中關(guān)于曲面迭代求交的原理介紹如下：為求得兩個(gè)曲面精確的交點(diǎn)，Newton-Raphson迭代法得到廣泛應(yīng)用，該法的優(yōu)點(diǎn)為

• 計(jì)算精度高，速度快，在初值選擇比較合理的情況下，一般僅需要迭代二到三次就可以使交點(diǎn)的精度從百分之幾提高到萬分之幾甚至百萬分之一的數(shù)量級(jí)。
• 適用范圍廣，只要能獲得曲面的幾何位置、切矢、法矢等信息，不論什么類型的曲面都可以使用迭代法。

其缺點(diǎn)是對(duì)初始值要求較嚴(yán)格，初始值選擇不當(dāng)，可能導(dǎo)致迭代不收斂，也就無法得到精確的交點(diǎn)。

在曲面求交等問題中，一般可根據(jù)參與變化的參數(shù)數(shù)量將迭代法分為三參數(shù)迭代法和四參數(shù)迭代法兩種類型。我們知道，一張參數(shù)曲面有兩個(gè)參數(shù)，兩張參數(shù)曲面共有四個(gè)參數(shù)變量。采用三參數(shù)迭代法時(shí)，兩個(gè)曲面的四個(gè)參數(shù)中只有三個(gè)參數(shù)參與迭代過程，而保持另一個(gè)參數(shù)固定不變，這實(shí)際上就是計(jì)算不變參數(shù)的等參數(shù)線與另一張曲面的交點(diǎn)。采用四參數(shù)迭代法時(shí)，兩張曲面的四個(gè)參數(shù)變量都參與迭代過程，四者都可能變化。兩種迭代法各有其優(yōu)缺點(diǎn)。在下述情況下以應(yīng)用三參數(shù)迭代法為宜：

• 要求將交點(diǎn)迭代至某參數(shù)線上，以利于后繼追蹤求交法中濾除無效初值點(diǎn)；
• 當(dāng)交線接近于參數(shù)邊界時(shí)，希望將交點(diǎn)迭代至準(zhǔn)確的邊界上，以便進(jìn)行裁剪等操作。

但對(duì)于一般交點(diǎn)，三參數(shù)法則未必適用。首先遇到的問題是在四個(gè)參數(shù)中選擇何者作為不變參數(shù)，固定參數(shù)選擇不當(dāng)可能降低迭代收斂速度以至根本不收斂，或者破壞交線拓樸結(jié)構(gòu)的正確性。迭代法本身不能夠成獨(dú)立的求交方法，主要在追蹤法中使用，OpenCASCADE中曲面求交追蹤法的類是IntWalk_PWalking。本文主要介紹OpenCASCADE曲面求交迭代法的類IntWalk_TheInt2S的用法及原理。

2 Newton迭代求交

OpenCASCADE中兩曲面求交迭代法由類IntWalk_TheInt2S實(shí)現(xiàn)，其類中主要函數(shù)有：

給定兩個(gè)曲面，和初始估計(jì)點(diǎn)在兩個(gè)曲面上的參數(shù)(u1, v1), (u2,v2)，迭代計(jì)算出精確交點(diǎn)。固定三參數(shù)的方式總共分四種類型IntImp_ConstIsoparametric：

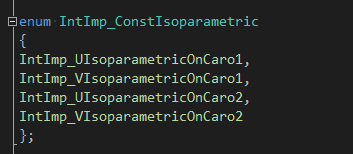
IntImp_UIsoparametricOnCaro1：是固定估計(jì)點(diǎn)在曲面1上的參數(shù)u；

IntImp_VIsoparametricOnCaro1：是固定估計(jì)點(diǎn)在曲面1上的參數(shù)v；

IntImp_UIsoparametricOnCaro2：是固定估計(jì)點(diǎn)在曲面2上的參數(shù)u；

IntImp_VIsoparametricOnCaro2：是固定估計(jì)點(diǎn)在曲面2上的參數(shù)v；

為了避免三參數(shù)迭代法找不到交點(diǎn)的情況，會(huì)在四個(gè)方向上分別進(jìn)行計(jì)算，總有一個(gè)方向上會(huì)找到交點(diǎn)，并將找到交點(diǎn)的參數(shù)固定情況返回：

在函數(shù)Perform()中通用求解迭代方程組，得到精確交點(diǎn)：

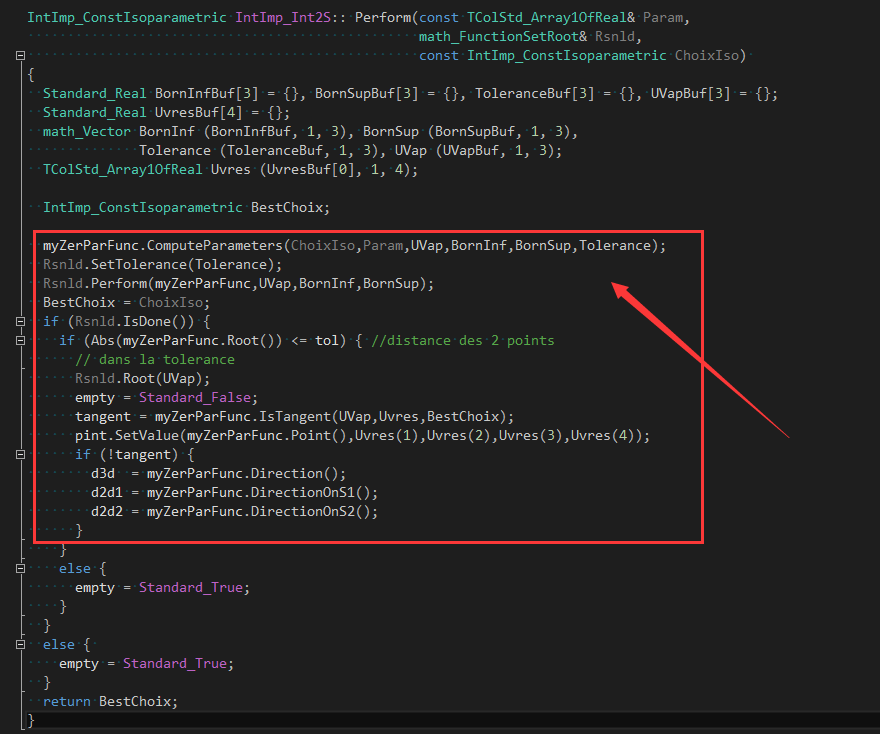
其中迭代方程組為成員變量myZerParFunc，方程組求解使用類math_FunctionSetRoot。由方程組求解類注釋可知，需要方程組的一階偏導(dǎo)數(shù)即梯度Gradient，采用的是Newton迭代法。若方程組有解Root且滿足精度要求，則保存下精確交點(diǎn)的坐標(biāo)值及在兩個(gè)曲面上的參數(shù)值等數(shù)據(jù)。

3 三參數(shù)迭代方程組

三參數(shù)迭代方程類為GeomInt_TheFunctionOfTheInt2SOfThePrmPrmSvSurfacesOfWLApprox,

是從類math_FunctionSetWithDerivatives派生的，即三參數(shù)迭代方程是個(gè)方程組(Function Set)。其定義在文件IntImp_ZerParFunc中，先使用函數(shù)ComputeParameters()根據(jù)固定參數(shù)類型來確定估計(jì)點(diǎn)的固定參數(shù)及另外三個(gè)參數(shù)變量的初始值：

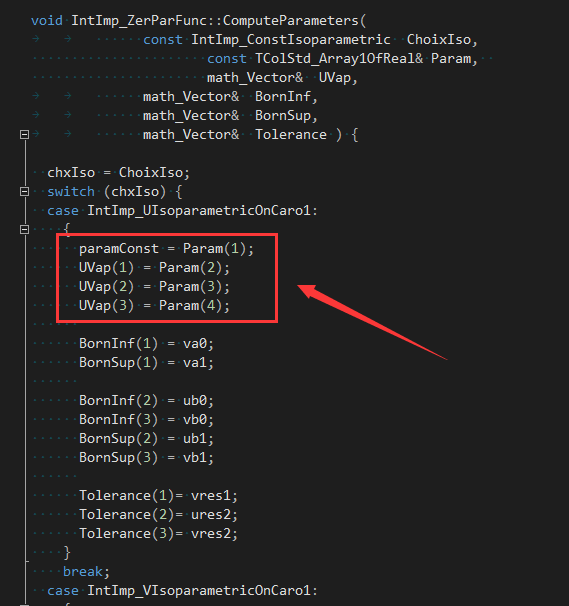
設(shè)兩個(gè)參數(shù)曲面S1(u1,v1)，S2(u2,v2)，并已知一交點(diǎn)的初估計(jì)點(diǎn)P0，P0點(diǎn)在兩張曲面上對(duì)應(yīng)的投影點(diǎn)分別為P1=S1(u0,v0)和P2=S2(s0,t0)。由于P0點(diǎn)為一估計(jì)點(diǎn)，所以P1和P2并不重合。設(shè)以s0作為固定參數(shù)，即當(dāng)固定參數(shù)類型為IntImp_UIsoparametricOnCaro1時(shí)，則問題轉(zhuǎn)化為求u*,v*,t*，使兩曲面片上的點(diǎn)S1(u*,v*)和S2(s0,t*)重合。建立方程組：

R(u,v,t)=S1(u,v) - S2(s0, t)

通過函數(shù)計(jì)算兩個(gè)曲面上的點(diǎn)pntsol1和pntsol2，得到三個(gè)變量的方程組的值。

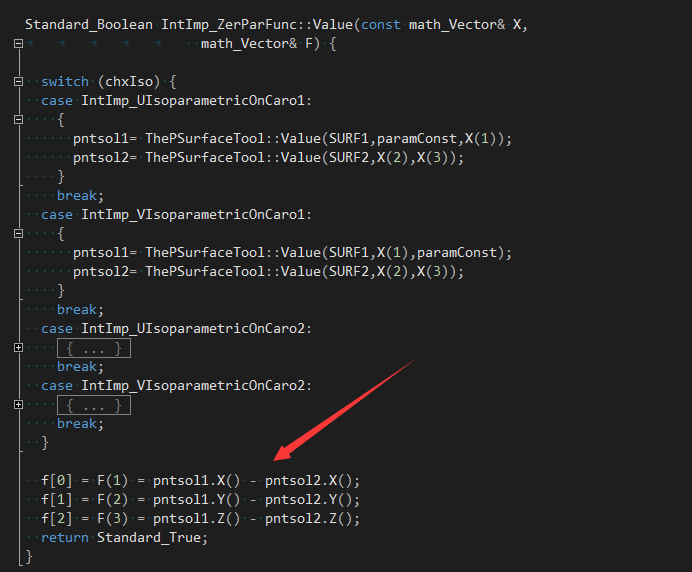
因?yàn)橐褂肗ewton迭代法，需要提供方程組的一階偏導(dǎo)數(shù)，即Jacobian矩陣：

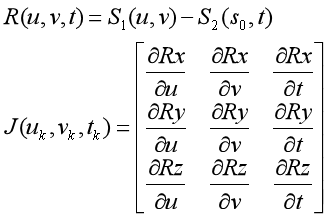
函數(shù)Derivatives()用來計(jì)算一階偏導(dǎo)數(shù)：

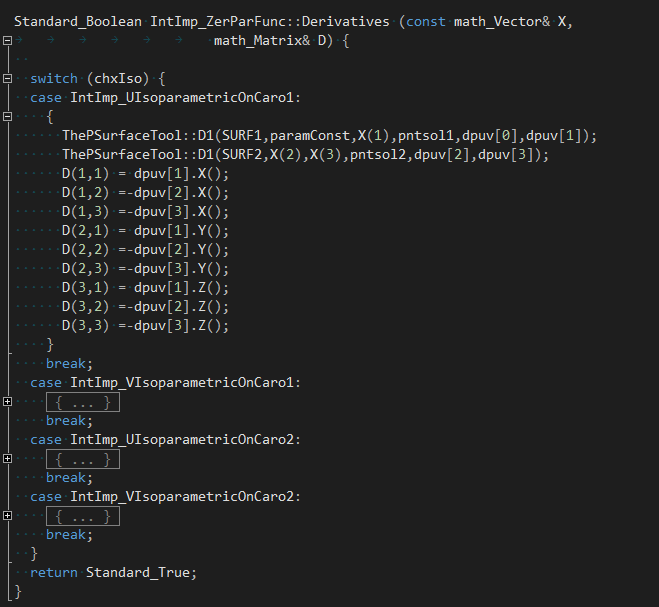
4 Conclusion

綜上所述，迭代法本身不能構(gòu)成一個(gè)獨(dú)立的求交方法，與所有不動(dòng)點(diǎn)迭代法一樣，應(yīng)用迭代法求交線之前，首先必須給出交點(diǎn)的初始估計(jì)值，而交點(diǎn)的初始值必須通過其他求交方法得到。因此，迭代交交常同其它求交方法結(jié)合使用，作為交點(diǎn)精化的一種手段。迭代法的主要過程是根據(jù)初始估計(jì)點(diǎn)的幾何性質(zhì)（如坐標(biāo)位置、切矢、法矢、曲率等）運(yùn)用Newton方法得到一個(gè)較原估計(jì)點(diǎn)更接近于目標(biāo)點(diǎn)（即精確交點(diǎn)）的估計(jì)點(diǎn)。如此反復(fù)進(jìn)行，直到求得的交點(diǎn)滿足所要求的精度。該法的優(yōu)點(diǎn)是在初值比較好時(shí)其收斂速度非?？?，而且能應(yīng)用于任意參數(shù)曲面包括Coons曲面和等距曲面，因此應(yīng)用非常廣泛，其主要缺點(diǎn)是對(duì)初始值要求比較苛刻，初始值 選擇不當(dāng)有可能導(dǎo)致迭代不收斂。

OpenCASCADE中曲面求交的迭代法也不是獨(dú)立的方法，與之配合的有離散網(wǎng)格求交得到初值，在追蹤中作用迭代法。迭代求交使用的是三參數(shù)迭代法，根據(jù)三參數(shù)迭代法的數(shù)學(xué)方程可知，需要計(jì)算曲面上參數(shù)對(duì)應(yīng)的點(diǎn)和切矢。