OpenCASCADE PCurve終極問(wèn)題
eryar@163.com
Abstract: Geometry Curves and Surfaces in BRep are parametric equations. So given a parametric space curve and a geometry surface can map to a 3d geometry curve. The parametric space curve is PCurve. When given a 3d geometry curve and surface, how to get the PCurve?
Keywords: OpenCASCADE, BRep, PCurve, Project, ProjLib
1 Introduction
看過(guò)《西游記》的對(duì)其中一些臺(tái)詞記憶深刻,像唐僧每次介紹自己時(shí)說(shuō)“貧僧唐三藏�,從東土大唐而來(lái),去往西天拜佛取經(jīng)��。”一句話點(diǎn)明哲學(xué)的終極問(wèn)題:我是誰(shuí)?我從哪里來(lái)��?我要到哪里去����?縱觀三藏的心路歷程可知,他從來(lái)就知道自己是誰(shuí)��,不管取經(jīng)路途多么艱辛困苦�,他總是初心不改����,志在其中�。
在學(xué)習(xí)新東西的時(shí)候,也會(huì)經(jīng)常會(huì)有這些問(wèn)題。如XXX是什么,怎么定義的。怎么生成XXX�?XXX有什么用�?能把這三個(gè)問(wèn)題回答清楚��,新東西基本就掌握了�。
本文主要來(lái)回答PCurve的這三個(gè)問(wèn)題����,即PCurve是什么?PCurve從哪里來(lái)��?PCurve有什么用�?幫助大家深入理解這個(gè)BRep表示法中的核心概念。
2 PCurve是什么
我們找到OpenCASCADE中的注釋對(duì)PCurve的描述:A 2D curve associated to the curve on surface in the parametric space of the surface��。字面意思是曲面上的一條三維曲線對(duì)應(yīng)到曲面的參數(shù)空間中的一條二維曲線����,即PCurve是Parametric Space Curve的縮寫。也提醒我們BRep中幾何的表達(dá)采用的是參數(shù)方程的形式,對(duì)于曲線是一個(gè)參數(shù)的方程C(u),而對(duì)于曲面是兩個(gè)參數(shù)的方程S(u, v)�。曲面的參數(shù)空間就是曲面參數(shù)方程的定義域��,是二維空間。給定曲面參數(shù)空間一條線(即PCurve)根據(jù)曲面的參數(shù)方程總是能映射到得到一條模型空間的三維曲線或退化的曲線�。
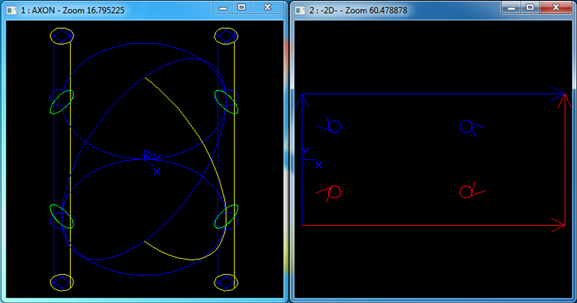
3 PCurve從哪里來(lái)
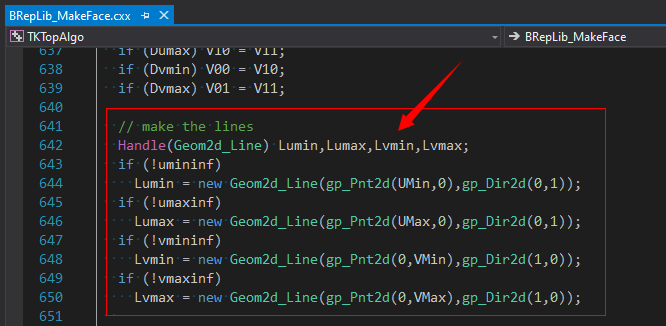
關(guān)于PCurve有兩個(gè)要素:一是Curve��,一是Surface�。在生成Face的代碼里,最關(guān)鍵的就是設(shè)置PCurve����。從生成Face的類BRepLib_MakeFace中,我們可以看到�,對(duì)于已經(jīng)有參數(shù)范圍的曲面�,其PCurve就是參數(shù)范圍在參數(shù)空間的一個(gè)矩形,這里是手動(dòng)創(chuàng)建的����。
那更一般的情況怎么辦呢?如已知曲面及曲面上的一條曲線��,怎么得到PCurve?在OpenCASCADE中提供了一個(gè)靜態(tài)函數(shù)來(lái)計(jì)算:

最終是調(diào)用類ProjLib_ProjectedCurve來(lái)計(jì)算的:
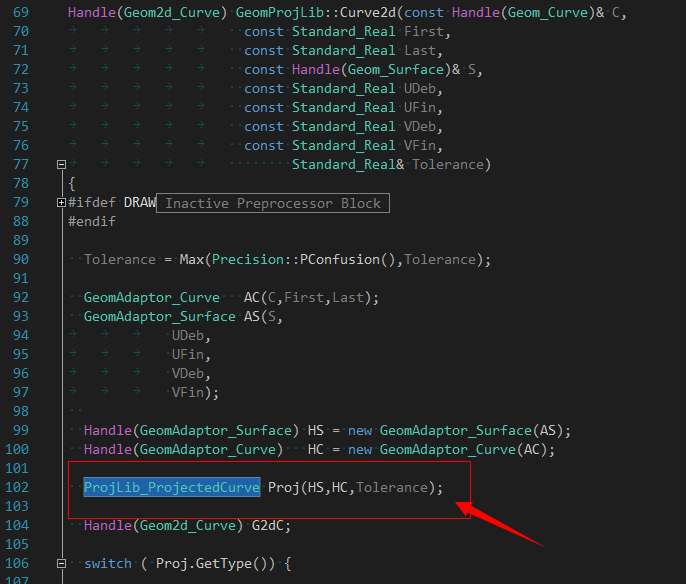
前面還介紹過(guò)了曲線向曲面投影的算法原理��,知道是通過(guò)計(jì)算曲線上的點(diǎn)與曲面法向上的交點(diǎn)來(lái)求出曲面上的擬合曲線��,這里的擬合曲線仍然是模型空間的三維曲線�。那么怎么計(jì)算出曲線在曲面參數(shù)空間的PCurve呢��?我們來(lái)看看類ProjLib_ComputeApprox��,從中找出答案��。
//=======================================================================
//function : Value
//purpose :
//=======================================================================
static gp_Pnt2d Function_Value(const Standard_Real U,
const Handle(Adaptor3d_Curve)& myCurve,
const Handle(Adaptor3d_Surface)& mySurface,
const Standard_Real U1,
const Standard_Real U2,
const Standard_Real V1,
const Standard_Real V2,
const Standard_Boolean UCouture,
const Standard_Boolean VCouture )
{
Standard_Real S = 0., T = 0.;
gp_Pnt P3d = myCurve->Value(U);
GeomAbs_SurfaceType SType = mySurface->GetType();
switch ( SType ) {
case GeomAbs_Plane:
{
gp_Pln Plane = mySurface->Plane();
ElSLib::Parameters( Plane, P3d, S, T);
break;
}
case GeomAbs_Cylinder:
{
gp_Cylinder Cylinder = mySurface->Cylinder();
ElSLib::Parameters( Cylinder, P3d, S, T);
break;
}
case GeomAbs_Cone:
{
gp_Cone Cone = mySurface->Cone();
ElSLib::Parameters( Cone, P3d, S, T);
break;
}
case GeomAbs_Sphere:
{
gp_Sphere Sphere = mySurface->Sphere();
ElSLib::Parameters(Sphere, P3d, S, T);
break;
}
case GeomAbs_Torus:
{
gp_Torus Torus = mySurface->Torus();
ElSLib::Parameters( Torus, P3d, S, T);
break;
}
default:
throw Standard_NoSuchObject("ProjLib_ComputeApprox::Value");
}
if ( UCouture) {
if(S < U1 || S > U2)
{
S = ElCLib::InPeriod(S, U1, U2);
}
}
if ( VCouture) {
if(SType == GeomAbs_Sphere) {
if ( Abs( S - U1 ) > M_PI ) {
T = M_PI - T;
S = M_PI + S;
}
if(S > U1 || S < U2)
S = ElCLib::InPeriod(S, U1, U2);
}
if(T < V1 || T > V2)
T = ElCLib::InPeriod(T, V1, V2);
}
return gp_Pnt2d(S, T);
}
上面是擬合PCurve的擬合函數(shù)����,從擬合函數(shù)的定義可知��,對(duì)于簡(jiǎn)單曲面上的曲線,給定參數(shù)U可以計(jì)算出曲線的點(diǎn)P3d��,根據(jù)P3d計(jì)算出曲面的參數(shù)空間的參數(shù)S, T,最后將參數(shù)空間的點(diǎn)返回。即將這些參數(shù)空間的二維點(diǎn)進(jìn)行擬合得到就是PCurve�。
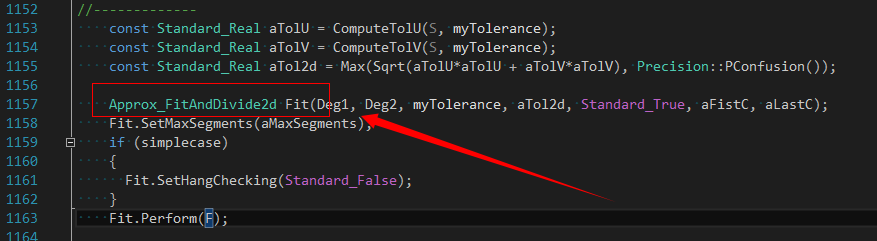
原來(lái)百思不得其解的問(wèn)題終于有了頭緒����,可以看出這個(gè)方法還是很巧妙的�。這里就回答了PCurve從哪來(lái)的問(wèn)題:若你知道PCurve,可以自己手動(dòng)設(shè)置;若對(duì)于任意曲面上曲線的PCurve,可以通過(guò)Project得到�。從中可以看出擬合功能的重要性��。
4 PCurve有什么用
從PCurve的定義上可以看出,通過(guò)PCurve相當(dāng)于建立了Edge與Face的聯(lián)系��。從目前的理解來(lái)看PCurve主要還是用在Mesh����,將Face網(wǎng)格化。因?yàn)榫W(wǎng)格化目前的算法主要還是在曲面的參數(shù)空間進(jìn)行三角剖分:
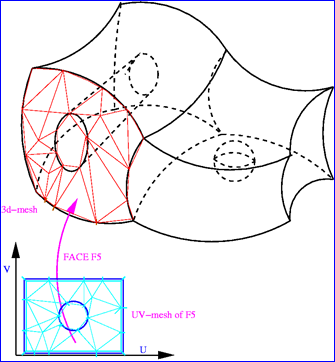
5 Conclusion
綜上所述�,在理解PCurve是什么后����,大家可以自己思考下��,如果讓你實(shí)現(xiàn)生成PCurve的算法�,你會(huì)怎么做呢��?PCurve除了用于Mesh����,還有哪些應(yīng)用呢��?期待大家的發(fā)掘�。
理解PCurve后����,相信OpenCASCADE的大部分源碼大家已能看懂��,為大家鉆研源碼打下基礎(chǔ)�。