OpenCASCADE 曲線向曲面投影
eryar@163.com
Abstract: Project a curve on a surface no matter the surface is a plane or BSpline Surface. The projected result curve are all BSpline Curve generated by approx algorithm.
Keywords: BRep, Project Curve Surface,
1 Introduction
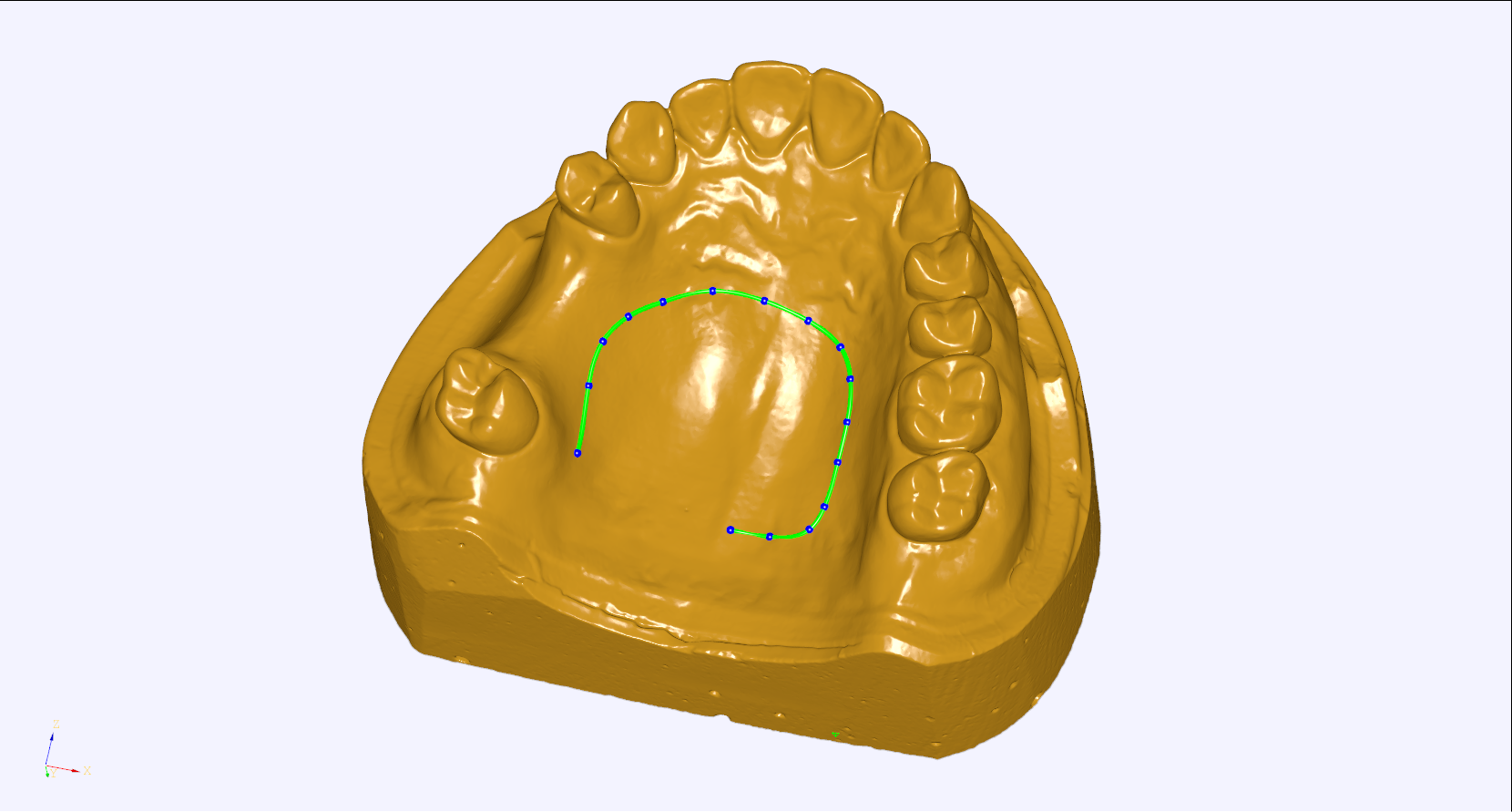
OpenCASCADE中提供了幾何曲線向曲面投影的功能,得到的投影線是曲面上的一條曲線。使用類GeomProjLib的靜態(tài)函數(shù)Project(C, S)和ProjectOnPlane(C, P, D)。

在畫法幾何與機(jī)械制圖中,機(jī)械圖樣的繪制是以投影法為依據(jù)的。本文主要介紹OpenCASCADE中曲線向曲面投影的實(shí)現(xiàn)原理。
2 Project On Plane
在畫法幾何中投射線互相平行的投影方法叫做平行投影。在平行投影中,以投射線與投影面的關(guān)系又可分為正投影法和斜投影法。投射線與投影面相傾斜的平行投影法,叫做斜投影法。投射線與投影面相垂直的平行投影法,叫做正投影法。工程上采用的正投影法來繪制圖樣。正投影法又因法國學(xué)者蒙若(G. Monge, 1746~1818)首次從理論上加以系統(tǒng)闡述而有蒙若法之稱。
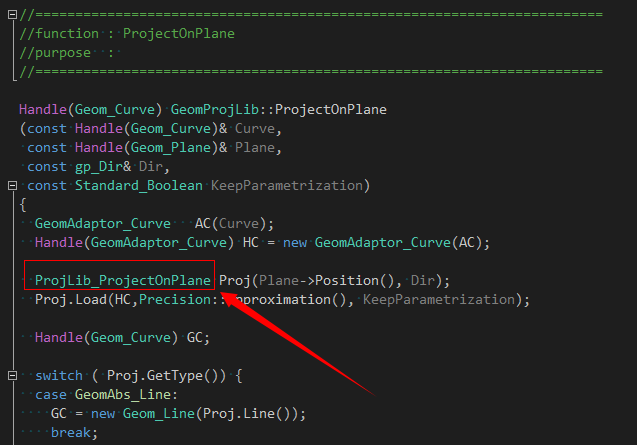
在OpenCASCADE中與平行投影對應(yīng)的類是ProjLib_ProjectOnPlane,其輸入數(shù)據(jù)有待投影的曲線Curve,投影平面Plane以及投影方向Dir。這里的投影方向Dir與投影平面法向不平行時(shí)為斜投影,投影方向Dir與投影平面法向平行時(shí)為正投影。
通過查看類ProjLib_ProjectOnPlane的源碼實(shí)現(xiàn),可以總結(jié)出這個(gè)算法的處理流程:

首先輸入數(shù)據(jù),有待投影的曲線、投影平面及投影方向等。如果投影曲線是特殊曲線,即簡單的曲線如直線、圓、橢圓等,計(jì)算其投影結(jié)果。結(jié)果可能還會是簡單的曲線。最后處理一般曲線的投影,這時(shí)主要使用擬合算法來生成投影曲線,結(jié)果都是B樣條曲線。
在這個(gè)類中我們也可以學(xué)習(xí)如何使用底層的曲線擬合功能。擬合算法的關(guān)鍵是定義擬合函數(shù)。如在此類中,定義的擬合函數(shù)ProjLib_OnPlane如下:

主要是實(shí)現(xiàn)其中的虛函數(shù)Value():

這個(gè)函數(shù)的作用是計(jì)算對應(yīng)曲線Curve的參數(shù)U的空間點(diǎn)在方向D上與平面Pl的交點(diǎn)。可以結(jié)合下圖寫出這個(gè)公式:
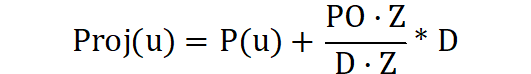
其中P(u)是曲線上對應(yīng)參數(shù)U的點(diǎn),D是投影方向,Z是平面的法向,O是平面的基點(diǎn)坐標(biāo)。設(shè)P(u)沿投影方向D的長度為x時(shí)與平面有交點(diǎn)P1,根據(jù)向量P(u)P1與平面法向Z的投影距離與向量P(u)O與平面法向Z的投影距離相等可以列出方程:x*D*Z = PO * Z解出x,即上式中方向D前面的分式。

在看懂這個(gè)公式的基礎(chǔ)上,建議同學(xué)們可以自己寫出求1階微分的公式:
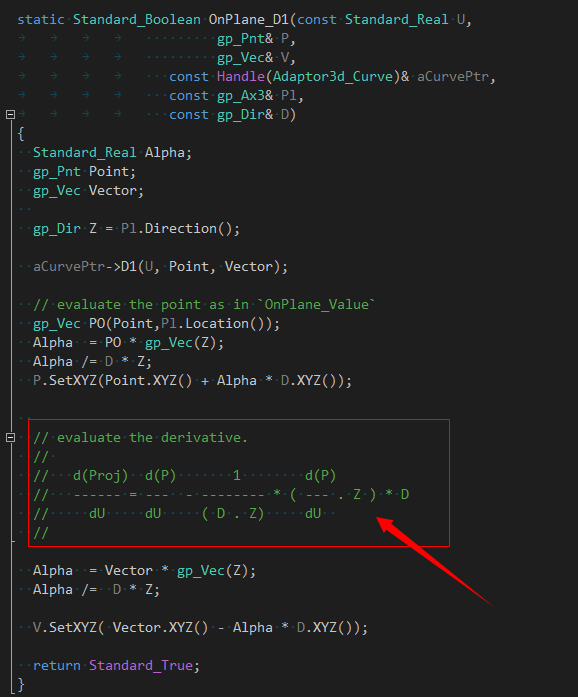
有了擬合函數(shù),就可以調(diào)用曲線擬合類來擬合投影曲線:

函數(shù)參數(shù)中最后一個(gè)是擬合曲線的返回值,即一條B樣條曲線。
3 Project On Surface
類ProjLib_ProjectOnSurface實(shí)現(xiàn)曲線向曲面上的投影,其注釋有“Constructs 3D-Curve from the normal projection of the curve on the surface”。其中Normal是曲面法向的意思,還是結(jié)合源碼來進(jìn)行說明。
曲線向曲面投影的處理流程與曲線向平面投影類似,關(guān)鍵都是擬合函數(shù)的定義。

從實(shí)現(xiàn)方法可以看出是通過計(jì)算點(diǎn)到曲面的極值來計(jì)算對應(yīng)曲線參數(shù)U的點(diǎn)與曲面的交點(diǎn)。這個(gè)交點(diǎn)與曲線參數(shù)U對應(yīng)的點(diǎn)的連線方向即曲面在交點(diǎn)處的法向。從而去理解曲面Normal投影的含義,因?yàn)樵贐Rep中對應(yīng)的有相應(yīng)的投影算法。
4 Conclusion
在OpenCASCADE中曲線向平面投影可以與機(jī)械制圖中的平行投影對應(yīng)起來。在處理曲線向曲面投影的算法主要是曲線擬合算法。結(jié)合源碼理解擬合函數(shù)的定義方法,通過對擬合函數(shù)的理解,還可以實(shí)現(xiàn)曲線向網(wǎng)格面的投影功能。