解析幾何之二次型

eryar@163.com

Abstract. 通過二次多項式的形式把二次曲線和二次曲面之間的求交問題統一成對將參數方程代入隱式方程得到問題的求解。

Key Words. Quadratic Form, Conic, Analytical Intersection

1. Introduction

二次型（quadratic form）：n個變量的二次多項式稱為二次型，即在一個多項式中，未知數的個數為任意多個，但每一項的次數都為2的多項式。線性代數的重要內容之一，它起源于幾何學中二次曲線方程和二次曲面方程化為標準形問題的研究。二次型理論與域的特征有關。

二次型是n個變量上的二次齊次多項式。下面給出一個、兩個、和三個變量的二次形式：

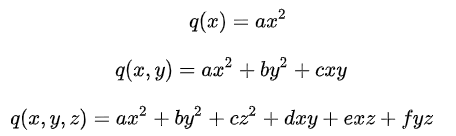
其中a, ...,f是系數。注意一般的二次函數和二次方程不是二次形式的例子，因為它們不總是齊次的，可能包含一次項和常數項。

幾何造型中的圓錐曲線Conic Curve與二次曲面Quadric是一般的二次方程，方程分別為：

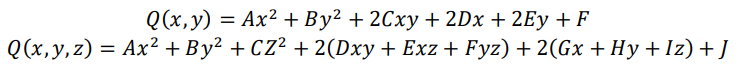
 在學習《線性代數》時也有關于二次型及其標準型的內容，在同濟第四版《線性代數》書中這樣寫到“二次型及其標準型，這樣一個問題，在許多理論問題或實際問題中常會遇到，現在我們把這類問題一般化，討論n個變量的二次齊次多項式的化簡問題。” 學這個有什么用啊？能解決哪些實際問題？下面我們看看二次型在實際問題中的應用。

2. Classification

在《工程技術中的偏微分方程》一書中，有二次型的一個應用，即對二次線性方程的分類Classification。我們從實際問題出發，可以推導并建立熱傳導方程，波動方程和Laplace方程，同時指出他們分別是拋物型、雙曲型和橢圓型三類方程的典型代表。設有二階線性方程

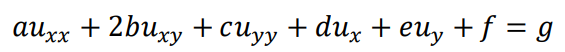
在解析幾何中，XOY平面上的二次曲線方程的一般形式：

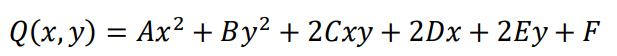
通過適當的坐標變換可以將上式化簡成橢圓、雙曲線和拋物線的標準方程，即對于任意二次圓錐曲線，都可以通過化成標準型的方法來判斷圓錐曲線的類型。根據不同的類型，選擇不同的求解方法。

3. Analytical Intersection

在《計算機圖形學基礎教程》書中有一章節“求交分類”，對幾何曲線曲面求交進行了分析。摘錄書中部分內容如下：

在幾何造型中，通常利用集合運算（并、交、差運算）實現復雜形體的構造，而集合運算（布爾運算）需要大量的求交運算。如何提高求交的實用性、穩定性、速度和精度等，對幾何造型系統至關重要。

在早期的幾何造型系統中，用多面體來表示形體。在這種多面體模型中，形體所有的表面都是平面，所有的邊都是直線段，因此求交計算主要是線段和平面的求交，求交問題的解決都相對簡單。

但多面體模型的缺點是明顯的。它只能近似表示形體。同時，復雜形體表面的離散會帶來巨大的數據量，要求計算機有較高的存儲量和運算速度。因此，有必要采用精確表示的形體模型，然而精確表示的形體也會給幾何造型系統引入復雜的幾何元素，也必然給幾何元素的求交帶來困難。

CSG模型是曾被廣泛使用的形體表示模型，在這種模型中，形體通過基本體素的組合來實現，基本體素通常是立方體、圓柱、圓錐、球和圓環體等。基于CSG表示的造型系統，引入了二次曲面體和基本體素后，二次曲面的求交在這些造型系統中是不可避免的。

當前的幾何造型系統，大多采用精確的邊界表示BREP模型。在這種表示法中，形體的邊界元素和某類幾何元素對應，它們可以是直線、圓弧、二次曲線、Bezier曲線和B樣條曲線等，也可以是平面、圓環面Torus、二次曲面、Bezier曲面和B樣條曲面等，求交情況十分復雜。

對于含有兩個變量的二次方程，對應的是二維二次圓錐曲線，在OpenCASCADE中的類gp_Circ2d, gp_Elips2d, gp_Hypr2d, gp_Parab2d, 他們都有一個函數Coefficients，能計算其二次型的系數。在解析幾何曲線求交計算包中IntAna2d，提供了一個類IntAna2d_Conic用來表示圓錐曲線，類IntAna2d_AnaIntersection可以對這些圓錐曲線進行求交計算。

對于含有三個變量的二次方程，對應的是三維二次曲面，在OpenCASCADE中的類有gp_Pln, gp_Sphere, gp_Cylinder, gp_Cone, 他們也都有一個函數Coefficients，能計算其二次型的系數。在解析幾何求交計算包中IntAna，提供了一個類IntAna_Quadric用來表示二次曲面。類IntAna_QuadQuad使用解析法（解方程）對兩個二次曲面進行求交計算；類IntAna_QuadQuadGeo使用幾何方法對兩個二次曲面進行求交計算；類IntAna_ConicQuad用來對圓錐曲線和二次曲面進行求交計算。

3.1   二次曲線與二次曲線求交

二次曲線與二次曲線求交指的是用代數方法來計算兩個曲線之間的相交情況，對應的類是IntAna2d_AnaIntersection。代數方法是利用代數運算，特別是求解代數方程的方法求解。由于圓錐曲線在其局部坐標系下具有標準的隱式方程和參數方程的噶啊，這類求交的策略是將坐標系變換到該圓錐曲線的局部坐標系下，一個圓錐曲線用隱式方程的形式表示，另一個圓錐曲線用參數方程的形式。對于曲線的參數方程而言，只有一個變量，將參數表示代入隱式方程即可獲得一個變量的方程。occt中相關代碼分析可參考：Intersection between 2d conic in OpenCASCADE

https://www.cnblogs.com/opencascade/p/6618865.html

3.2   二次曲線與二次曲面求交

二次曲線與二次曲面的求交計算，可以把二次曲線的參數形式代入二次曲面的隱式方程，得到關于參數的4次方程。然后用4次方程的求要公式計算出交點。occt中相關代碼分析可參考：對應的類是IntAna_IntConicQuad

解析幾何求交之直線與二次曲面

https://www.cnblogs.com/opencascade/p/IntAna_IntConicQuad.html

解析幾何求交之圓與二次曲面

https://www.cnblogs.com/opencascade/p/IntAna_Circle.html 

3.3   二次曲面與二次曲面求交

二次曲面與二次曲面的求交計算，也可以把二次曲面的參數形式代入二次曲面的隱式方程。對應的類是IntAna_QuadQuad，其中對圓柱與二次曲面的求交計算源碼注釋如下圖所示：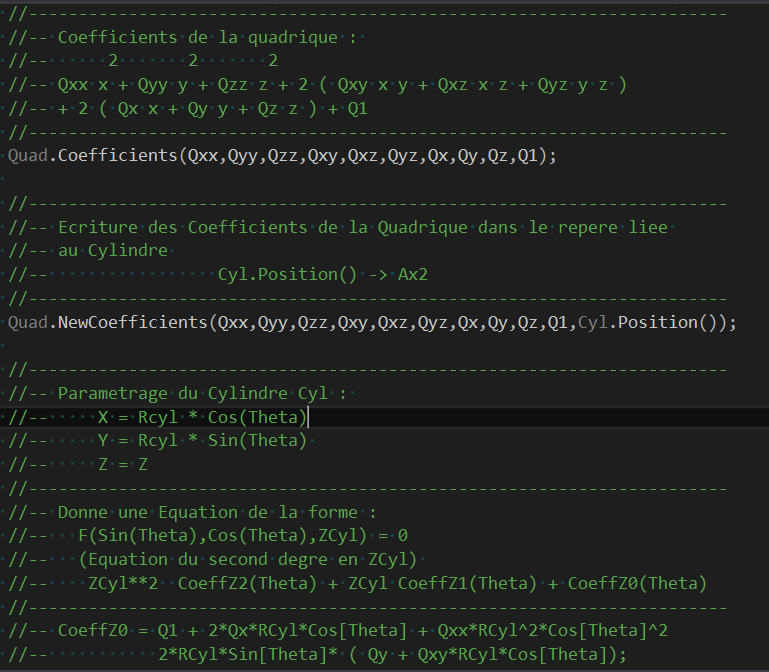 

3.4   二次曲面與二次曲面求交幾何方法

幾何方法求交是利用幾何的方法，對參與求交的曲面的形狀、位置以及方向等幾何特點進行計算和判斷，識別出交線的形狀和類型，從而精確求出交線。對于一些交線退化或相切的情況，用幾何方法可以更加迅速和可靠。在occt中對應的類是IntAna_IntConicQuad。關于源碼分析可以參考：

OpenCASCADE 平面與球面求交

https://www.cnblogs.com/opencascade/p/PlaneSphere.html

OpenCASCADE 平面求交

https://www.cnblogs.com/opencascade/p/IntAna_PlanePlane.html

4. Conclusion

綜上所述，通過二次多項式的形式把二次曲線和二次曲面之間的求交問題統一成對將參數方程代入隱式方程得到問題的求解。提供二次曲面幾何求交算法，可以更快地得到結果。其實對于不包含B樣條曲線曲面的模型（如CSG模型）來說，IntAna2d和IntAna已經可以實現求交，所以對于這些模型求交計算很快。

這也解決了我以前的一個疑問：為什么沒有解析的三維圓錐曲線與曲線求交算法？因為三維圓錐曲線本身就是兩個二次曲面的交線。沒有像二維圓錐曲線和二次曲面那樣有隱式方程。

5. References

5.1   同濟大學數學教研室. 高等數學. 第四版 高等教育出版社

5.2   同濟大學應用數學系. 線性代數. 第四版 高等教育出版社

5.3   潘祖梁, 陳仲慈. 工程技術中的偏微分方程. 浙江大學出版社

5.4   丘維聲. 解析幾何. 北京大學出版社

5.5   孫家廣, 胡事民. 計算機圖形學基礎教程. 清華大學出版社

為了方便大家在移動端也能看到我的博文和討論交流，現已注冊微信公眾號，歡迎大家掃描下方二維碼關注。