Posted on 2021-02-08 13:29
eryar 閱讀(1315)
評論(0) 編輯 收藏 引用 所屬分類:
2.OpenCASCADE

OpenCASCADE Rolling Ball
eryar@163.com
在《The NURBS Book》書中引入了三邊球面片(Three-sided Spherical Surface)的概念:
當三個曲面兩兩相交時,會使三邊界曲線交于一個角點(如圖a),由于在產品零部件中�����,尖邊和尖角經常是我們不希望有的��,一方面是會有應力集中,另一方面尖的部分容易使人受傷。因此,經常需要對曲面的尖邊和尖角進行處理�,使其變得光滑,這種操作通常稱為“圓角”或“倒角”,所得到的曲面稱為圓角曲面(Fillet Surface)�。一個常用的獲得圓角曲面的概念性方法是“滾球法”(Rolling marble)�����。設一個半徑為R的小球在物體內側沿著所有的邊界曲線滾動���,得到圖b中所示的曲面S4-S7, S4-S6為倒邊曲面(edge fillet)�,S7為倒角曲面(Corner fillet)���。倒角曲面S7是一個三邊曲面片(Three-side patch)����。

在實際造型時也經常需要對曲面連接部分進行光滑處理�����,除了常見的倒角Chamfer和倒圓Fillet以外�,opencascade也提供了rolling ball的造型算法用來對相邊曲面進行圓滑處理����,如下圖所示: 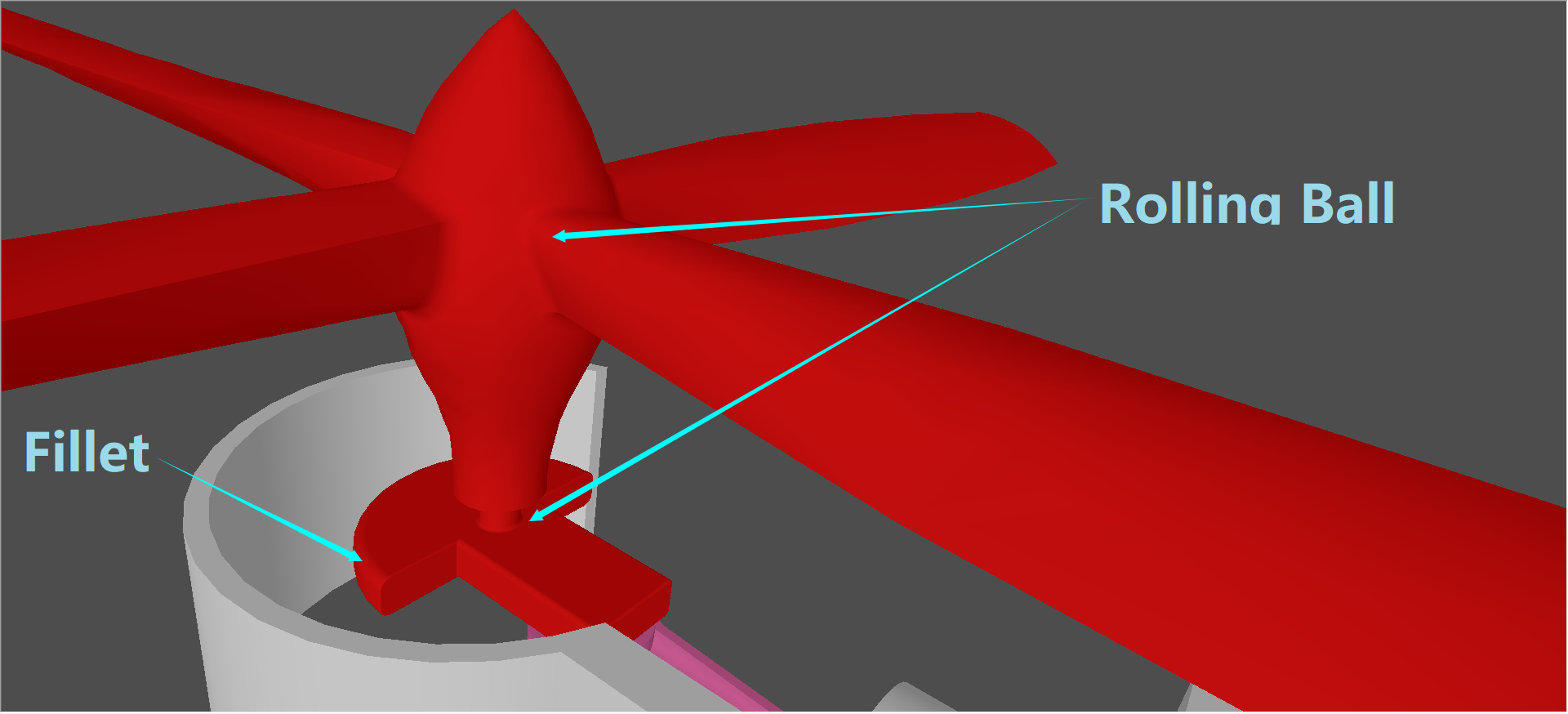
如下圖所示為對圓柱相連部分使用“Rolling Ball”生成一個圓滑過渡的圓弧曲面�。
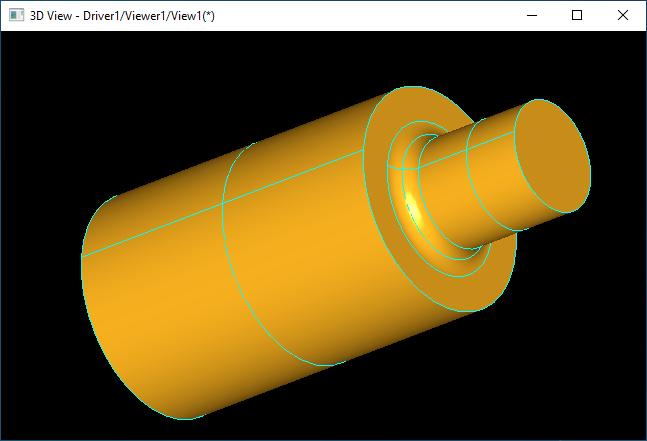
對于這種對稱的模型�,也可以使用旋轉造型算法��,把軸的外輪廓構造出來,再繞軸線旋轉一周也可以得到��。當相連曲面部分不對稱的時候���,旋轉造型也無能為力了����。
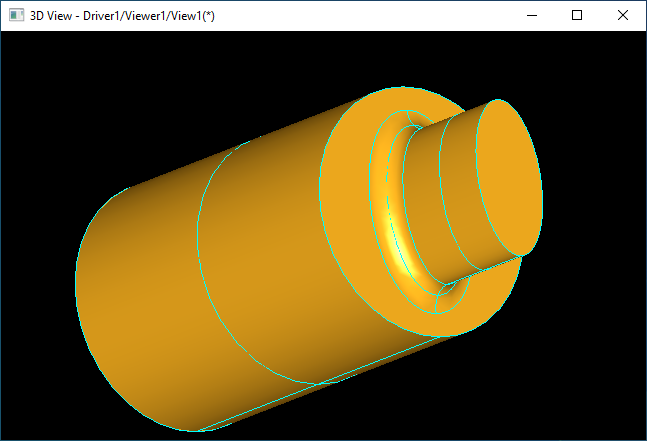
如上圖所示��,當相連接部分是不對稱的曲線橢圓時��,旋轉造型算法已經不適用��,這時就需要使用“滾球法”來對連接部分進行處理�。對于更復雜的情況����,如下圖所示的也適用���。
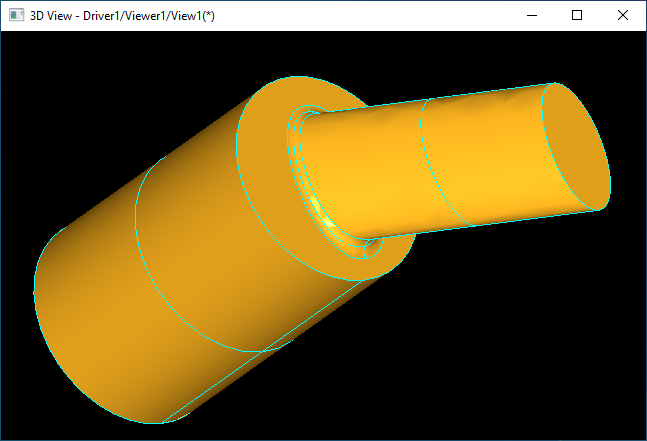
這里先引入opencascade中對相連曲面圓滑處理的造型算法“滾球法”Rolling Ball,有興趣的同學可以自己嘗試���。對實現原理感興趣的,可以自己Debug源碼����。希望有更多人去深究源碼,做到知其所以然��,提高數學的應用水平�。
為了方便大家在移動端也能看到我的博文和討論交流�,現已注冊微信公眾號�����,歡迎大家掃描下方二維碼關注。
