OpenCASCADE 平面與球面求交
OpenCASCADE提供了類IntAna_QuadQuadGeo用來計算兩個二次曲面quadric(球面、圓柱面、圓錐面及平面,平面是二次曲面的特例)之間的交線。他們之間可能的結果有:
l 一個點
l 一條或兩條直線
l 一個點和一條直線
l 圓
l 橢圓
l 拋物線
l 雙曲線

將源碼結合《高等數學》、《解析幾何》等書,可以來學習如何將理論付諸實踐。本文主要介紹這個類中平面與球面求交的源碼實現。 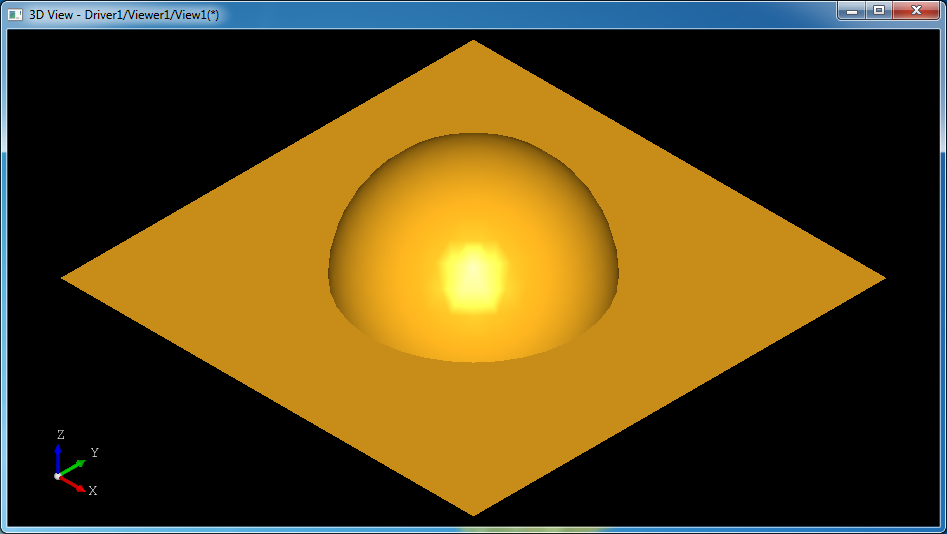
將源碼列出如下:
void IntAna_QuadQuadGeo::Perform( const gp_Pln& P ,const gp_Sphere& S) { done = Standard_False; Standard_Real A,B,C,D,dist, radius; Standard_Real X,Y,Z; nbint = 0; // debug JAG : on met typeres = IntAna_Empty par defaut... typeres = IntAna_Empty; P.Coefficients(A,B,C,D); S.Location().Coord(X,Y,Z); radius = S.Radius(); dist = A * X + B * Y + C * Z + D; if (Abs( Abs(dist) - radius) < Epsilon(radius)) { // on a une seule solution : le point projection du centre de la sphere // sur le plan nbint = 1; typeres = IntAna_Point; pt1.SetCoord(X - dist*A, Y - dist*B, Z - dist*C); } else if (Abs(dist) < radius) { // on a un cercle solution nbint = 1; typeres = IntAna_Circle; pt1.SetCoord(X - dist*A, Y - dist*B, Z - dist*C); dir1 = P.Axis().Direction(); if(P.Direct()==Standard_False) dir1.Reverse(); dir2 = P.Position().XDirection(); param1 = Sqrt(radius*radius - dist*dist); } param2bis=0.0; //-- pour eviter param2bis not used .... done = Standard_True; }
理解上述代碼需要有平面一般方程的概念及點到平面的距離計算公式:
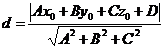
源碼實現步驟如下:
l 取出平面一般方程的系數:A,B,C,D及球心坐標X,Y,Z;
l 計算球心到平面的距離dist;
l 若距離dist等于球面的半徑,則平面為球面的切平面,只有一個交點;
l 若距離dist小于球面的半徑,則平面與球面的交線為圓;
其中需要注意的是在獲取平面一般方程的參數時,平面的法向為單位向量,所以在計算球心到平面的距離時的分母為1。
從上述代碼可以看出OpenCASCADE的算法類的特點:即都有一個算法完成狀態的函數IsDone(),通過成員變量done來設置,算法執行前都設置成false,算法成功后設置成true。還有一個前綴在變量名和函數名中很普遍,就是nb,是數量Number的縮寫,這里是一個成員變量nbint,即相交的數量。
為了方便大家在移動端也能看到我的博文和討論交流,現已注冊微信公眾號,歡迎大家掃描下方二維碼關注。





