OpenCASCADE直線與平面求交
在《解析幾何》相關的書中都給出了直線和平面的一般方程和參數方程。其中直線的一般方程有點向式形式的。
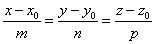
由于過空間一點可作且只能作一條直線平行于已知直線,所以當直線上一點(x0, y0, z0)和它的一方向向量(m,n,p)為已知時,直線就完全確定了。所以在OpenCASCADE中直線類gp_Lin有一個構造函數:
gp_Lin (const gp_Pnt &P, const gp_Dir &V) 即通過點和方向來構造直線。由直線的點向式方程容易導出直線的參數方程:
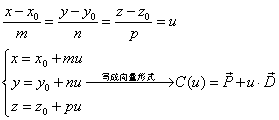
其中OpenCASCADE的直線是用參數方程來表示的。
同理對于平面而言,過空間一點可以作而且只能作一平面垂直于一已知直線,所以平面的一點(x0,y0,z0)和它的一個法線方向(A, B, C)為已知時,平面就完全確定了。所以平面方程也有點向式的:
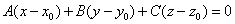
從一個點和兩個不共線的向量確定一個平面作為討論的出發點,可以得出平面的參數方程:
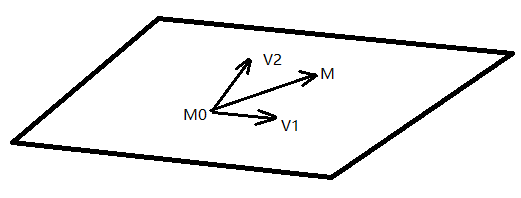
如上圖所示,已知一個點M0(x0,y0,z0),向量v1(x1,y1,z1)和向量v2(x2,y2,z2),我們來求點M0和向量V1,V2確定的平面方程。點M(x,y,z)在平面上的充要條件是向量M0M與V1, V2共面。因為向量V1, V2不平行,所以共面的充要條件是存在唯一的一對實數u, v使:
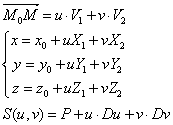
向量M0M和V1,V2共面的充要條件是:

根據平面的參數方程可知,要確定一個平面從參數方程的角度來看需要一個點和兩個方向。從參數方程推導出一般方程的過程也是計算平面一般方程系數的方法。
根據直線的參數方程及平面的一般方程可以推導出直線與平面交點的計算公式,推導過程如下:
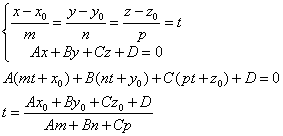
從上面的推導過程可以看出,計算直線與平面的交點主要就是計算參數t,當t求出后代入直線參數方程即可得到交點坐標。從參數t的計算公式可知,有個特殊情況就是分母為零的情況,此時是直線與平面平行共面需要特別處理。
在OpenCASCADE中提供了直線與平面求交的計算類IntAna_IntConicQuad,其實現源碼如下:
void IntAna_IntConicQuad::Perform (const gp_Lin& L, const gp_Pln& P, const Standard_Real Tolang, const Standard_Real Tol, const Standard_Real Len) { // Tolang represente la tolerance angulaire a partir de laquelle on considere // que l angle entre 2 vecteurs est nul. On raisonnera sur le cosinus de cet // angle, (on a Cos(t) equivalent a t au voisinage de Pi/2). done=Standard_False; Standard_Real A,B,C,D; Standard_Real Al,Bl,Cl; Standard_Real Dis,Direc; P.Coefficients(A,B,C,D); gp_Pnt Orig(L.Location()); L.Direction().Coord(Al,Bl,Cl); Direc=A*Al+B*Bl+C*Cl; Dis = A*Orig.X() + B*Orig.Y() + C*Orig.Z() + D; // parallel=Standard_False; if (Abs(Direc) < Tolang) { parallel=Standard_True; if (Len!=0 && Direc!=0) { //check the distance from bounding point of the line to the plane gp_Pnt aP1, aP2; // aP1.SetCoord(Orig.X()-Dis*A, Orig.Y()-Dis*B, Orig.Z()-Dis*C); aP2.SetCoord(aP1.X()+Len*Al, aP1.Y()+Len*Bl, aP1.Z()+Len*Cl); if (P.Distance(aP2) > Tol) { parallel=Standard_False; } } } if (parallel) { if (Abs(Dis) < Tolang) { inquadric=Standard_True; } else { inquadric=Standard_False; } } else { parallel=Standard_False; inquadric=Standard_False; nbpts = 1; paramonc [0] = - Dis/Direc; pnts[0].SetCoord(Orig.X()+paramonc[0]*Al, Orig.Y()+paramonc[0]*Bl, Orig.Z()+paramonc[0]*Cl); } done=Standard_True; }
從上述代碼中可以看出其計算思路也是先計算參數t,還加了一個特殊用法,即當參數Len!=0且參數t的分母!=0時重新判斷直線與平面的平行狀態。這個用法雖然有平行狀態的重新判斷,但是如果不平行沒有計算交點的處理。所以使用這個函數時,參數Len可以用默認值0,即不用這段處理邏輯。還有個不嚴謹的地方是這里的實數判斷沒有用區間判斷法。





