Posted on 2019-05-29 21:02
eryar 閱讀(1651)
評論(0) 編輯 收藏 引用 所屬分類:
2.OpenCASCADE

OpenCASCADE點向平面投影
OpenCASCADE的ProjLib類提供了解析曲線(直線、圓、橢圓、拋物線、雙曲線)向解析曲面(平面、圓柱面、圓錐面、球面、圓環面)投影的功能,主要用來計算三維曲線在二維參數空間的參數。
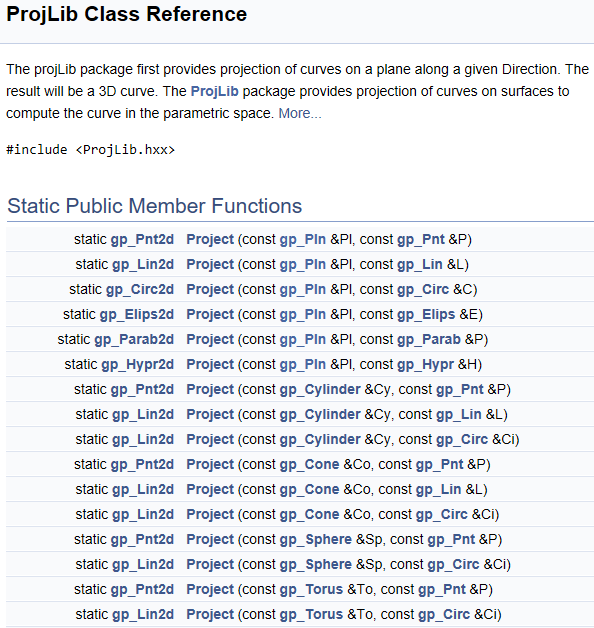
其中點向平面投影是最簡單的情況,本文主要介紹點向平面投影的注意事項。ProjLib類是個工具類,因為其函數都是靜態函數。點向平面投影很簡單,直接用ProjLib::Project(aPlane, aPoint)即可。
其實現代碼如下:
gp_Pnt2d ProjLib::Project(const gp_Pln& Pl, const gp_Pnt& P)
{
Standard_Real U, V;
ElSLib::Parameters(Pl, P, U, V);
return gp_Pnt2d(U,V);
}
inline void ElSLib::Parameters(const gp_Pln& Pl,
const gp_Pnt& P,
Standard_Real& U,
Standard_Real& V) {
ElSLib::PlaneParameters(Pl.Position(),P,U,V);
}
void ElSLib::PlaneParameters (const gp_Ax3& Pos,
const gp_Pnt& P,
Standard_Real& U,
Standard_Real& V)
{
gp_Trsf T;
T.SetTransformation (Pos);
gp_Pnt Ploc = P.Transformed (T);
U = Ploc.X();
V = Ploc.Y();
}
從上面的代碼可以看出,點向平面投影實現就是將點變換到平面所在的坐標系中。使用這個類向平面投影要注意的事項是平面的構造。平面gp_Pln有如下構造函數:

l 默認構造函數:構造了一個XOY平面
l 基于一個坐標系gp_Ax3構造平面
l 基于一個點和一個方向構造平面
l 基于平面的系數方程,即AX+BY+CZ+D=0
前兩個構造函數很清晰,而第三個構造函數即基于一個點和一個方向構造平面的方式沒有明確,注釋不清晰。這里的方向指定了平面的法向,但是還缺少一個方向來確定一個坐標系,所以使用這個構造函數來生成平面的時候,需要理解其生成另外一個方向的算法是不是自己需要的。
gp_Pln::gp_Pln (const gp_Pnt& P,
const gp_Dir& V)
{
Standard_Real A = V.X();
Standard_Real B = V.Y();
Standard_Real C = V.Z();
Standard_Real Aabs = A;
if (Aabs < 0) Aabs = - Aabs;
Standard_Real Babs = B;
if (Babs < 0) Babs = - Babs;
Standard_Real Cabs = C;
if (Cabs < 0) Cabs = - Cabs;
// pour determiner l'axe X :
// on dit que le produit scalaire Vx.V = 0.
// et on recherche le max(A,B,C) pour faire la division.
// l'une des coordonnees du vecteur est nulle.
if( Babs <= Aabs && Babs <= Cabs) {
if (Aabs > Cabs) pos = gp_Ax3 (P, V, gp_Dir (-C,0., A));
else pos = gp_Ax3 (P, V, gp_Dir ( C,0.,-A));
}
else if( Aabs <= Babs && Aabs <= Cabs) {
if (Babs > Cabs) pos = gp_Ax3 (P, V, gp_Dir (0.,-C, B));
else pos = gp_Ax3 (P, V, gp_Dir (0., C,-B));
}
else {
if (Aabs > Babs) pos = gp_Ax3 (P, V, gp_Dir (-B, A,0.));
else pos = gp_Ax3 (P, V, gp_Dir ( B,-A,0.));
}
}
當這里確定平面坐標系的方式與需要的不一致時,在使用投影算法的時候就會產生問題。