Posted on 2019-02-21 22:05
eryar 閱讀(1824)
評論(0) 編輯 收藏 引用 所屬分類:
2.OpenCASCADE

解析幾何求交之圓與二次曲面
eryar@163.com
Abstract. OpenCASCADE provides the analytic intersection between a conic and a quadric in the package IntAna.
Key Words. Analytic geometry, intersection, coninc, quadric
1. Introduction
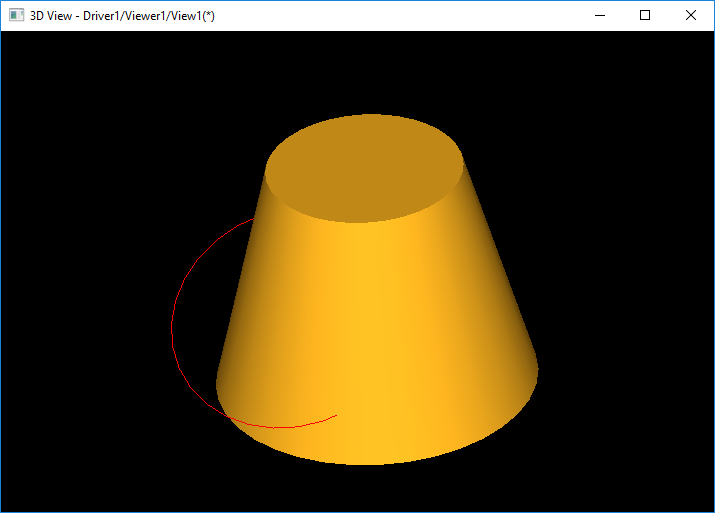
OpenCASCADE中的包IntAna提供了解析幾何曲線(二次曲線)與解析曲面(二次曲面)求交、解析曲面與解析曲面求交的功能。其中IntAna分別是Intersection Analytic的前三個字母縮寫,表示解析幾何求交。
我們學過了《線性代數》中的二次型,其中二次型在解析幾何中的一個應用就是二次曲線和二次曲面方程的化簡及其性質的分析。
本文主要結合源碼分析圓與二次曲面求交的實現,其他二次曲線與二次曲面求交的可以依此類推。
2. Quadratic form
在解析幾何中,為了便于研究二次曲線
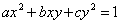
的幾何性質,我們可以選擇適當的坐標旋轉變換
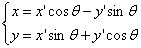
把方程化成標準形式:
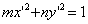
根據標準形式中的系數來分析這個二次曲線是什么曲線,即圓、橢圓、拋物線、雙曲線。
在OpenCASCADE中解析幾何的二次曲面有以下幾種類型:
l gp_Pln:平面可看作二次曲面的特例
l gp_Sphere:解析球面
l gp_Cylinder:解析柱面
l gp_Cone:解析錐面
這些解析曲面都可以統一使用二次多項式來表示,即這個二次多項式的系數確定了一個二次曲面。OpenCASCADE中相應的類是IntAna_Quaric:
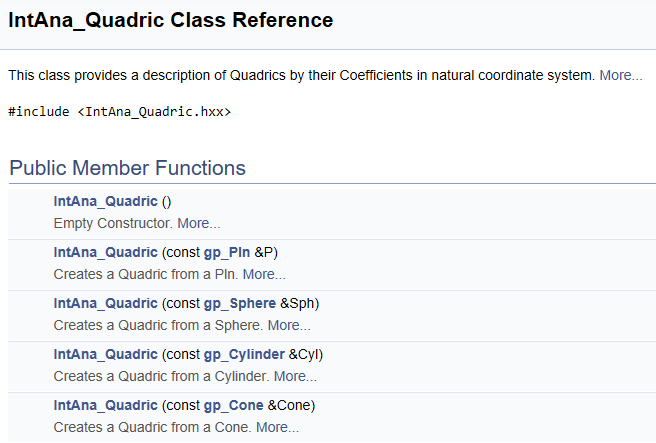
3. Math Trigonometric Function Roots
OpenCASCADE中類IntAna_IntConicQuad中提供了二次曲線與二次曲面求交功能,其中計算圓與二次曲面相交的函數是:
//! Creates the intersection between a circle and a quadric.
Standard_EXPORT IntAna_IntConicQuad(const gp_Circ& C, const IntAna_Quadric& Q);
其實現原碼中注釋如下:
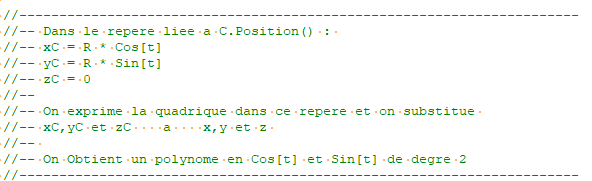
根據其注釋,可知其計算過程如下:將圓的方程在其局部坐標系中用參數形式表示,

將二次曲面方程的系數也變換到圓的坐標系中,因為圓的參數方程中為0,所以將圓的參數方程代入二次曲面的方程后,和z相關的項的系數都可以簡化了。
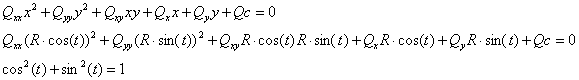
得到一個三角函數的方程后,這時就要引入基礎模塊中的數學工具集來解決問題了。
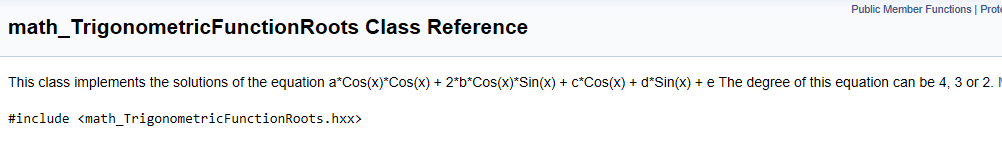
類math_TrigonometricFunctionRoots主要用于對如下形式的三角函數方程進行求解:
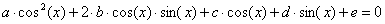
4. Conclusion
對于圓與二次曲面求交的實現來看,也可以不用變換二次曲面的坐標系,直接將圓的參數方程代入曲面的二次方程中:
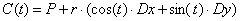
最終化簡也可得到一個三角函數方程,但是計算量與變換曲面坐標系對比來看會更大。
從上面的源碼分析可知,在OpenCASCADE中對于解析曲線與曲面求交使用二次多項式系數來表示的。通過將二次曲線用參數形式的方程來表示,并代入二次曲面的方程,化簡后直接使用math包中的工具(多項式方程求解和三角函數求解工具)對方程進行求解。
5. References
1. 同濟大學應用數學系. 線性代數(第四版). 高等教育出版社
2. 丘維聲. 解析幾何. 北京大學出版社
為了方便大家在移動端也能看到我的博文和討論交流,現已注冊微信公眾號,歡迎大家掃描下方二維碼關注。
