OpenCASCADE解非線性方程組
eryar@163.com
Abstract. 在科學技術領域里常常提出求解非線性方程組的問題,例如,用非線性函數擬合實驗數據問題、非線性網絡問題、幾何上的曲線曲面求交問題等。OpenCASCADE中有關于非線性方程組定義的類及其求解類,本文主要介紹如何在OpenCASCADE中定義非線性方程組,及對其進行求解。
Key Words. Function Set, Function Set Root, Newton Raphson Algorithm
1.Introduction
在科學技術領域里常常提出求解非線性方程組的問題,例如,用非線性函數擬合實驗數據問題、非線性網絡問題等。在幾何造型中很多問題也可以利用非線性方程組來解決。如曲線的光順,曲線求交、曲面求交、Blend造型問題等。
OpenCASCADE提供了非線性方程組的類math_FunctionSet,可以先從類圖上來看看有哪些算法使用了這個類:

圖1 曲線光順包FaireCurve
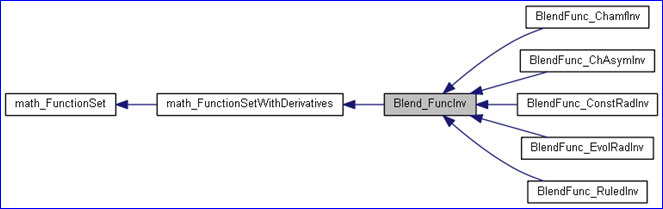
圖2 Blending Surface between two surfaces
感興趣的同學可以自己打開OpenCASCADE的類索引文件查看。可以看到很多算法涉及到方程組的求解問題。本文主要介紹如何定義非線性方程組及對其進行求解。理解這些套路后,對math_FunctionSet相關的派生類及其用用途就會有個清晰的認識,便于對源碼的理解。
2.Function Set Definition
設有非線性方程組
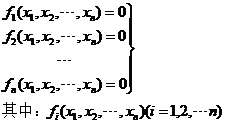
為實變量的非線方程函數。引入向量形式表示,引進記號:

于是非線性方程組可以簡單記作:F(x)=0。我們的問題是尋求X使F(X)=0,這個X就是非線性方程組的解。
OpenCASCADE中使用類math_FunctionSet來表示方程組,這是個抽象類,定義了如下純虛函數:
l NbVariables():變量的個數,即末知量的個數;
l NbEquations():方程的個數,即方程組中有幾個方程;
l Value(const math_Vector&X, math_Vector& F):方程組的值,即代入變量每個方程的值;
3.Function Set Root Algorithm
解非線性方程組的牛頓法和解方程式的思路一樣,要求方程有一階導數。而非線性方程組即是要求有偏導數。由fi(x)偏導數作成的矩陣記為J(x)或F’(x),稱為F(x)的Jacobi矩陣:

求解非線性方程組的牛頓法為:
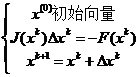
其中xk為方程線的近似解向量。
OpenCASCADE中也提供了非線性方程組的求解類,如:math_FunctionSetRoot,math_NewtonFunctionSetRoot。而使用這些類的輸入都是要求具有一階偏導數的線性方程組的定義math_FunctionSetWithDerivaties。這個類定義了具有一階偏導數的非線性方程組,其純虛函數除了前面說明的幾個以外,還增加了如下兩個:
l Derivatives(const math_Vector& X, math_Matrix& D):一階偏導數值,即計算Jacobi矩陣;
l Values(const math_Vector& X, math_Vector& F, math_Matrix& D):計算方程的值及一階偏導數矩陣Jacobi矩陣。
4.Code Example
下面給出一個具體的例子來說明這些類的用法。設有非線性方程組:
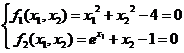
從幾何上看其解就是圓心在原點,半徑為2的圓與曲線的交點:
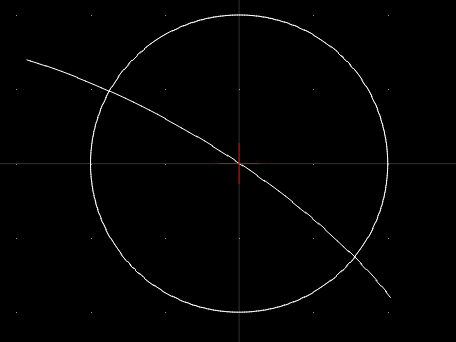
圖3 圓與曲線求交
下面我們使用OpenCASCADE來對上述問題進行求解。首先定義這個非線性方程組:
#include <math_FunctionSet.hxx>
#include <math_FunctionSetWithDerivatives.hxx>
#include <math_FunctionSetRoot.hxx>
#pragma comment(lib, "TKernel.lib")
#pragma comment(lib, "TKMath.lib")
class MyFunctionSet : public math_FunctionSetWithDerivatives
{
public:
virtual Standard_Integer NbVariables() const
{
return 2;
}
virtual Standard_Integer NbEquations() const
{
return 2;
}
virtual Standard_Boolean Value(const math_Vector& X, math_Vector& F)
{
F(1) = X(1) * X(1) + X(2) * X(2) - 4.0;
F(2) = Pow(M_E, X(1)) + X(2) - 1.0;
return Standard_True;
}
virtual Standard_Boolean Derivatives(const math_Vector& X, math_Matrix& D)
{
// matrix D is Jacobi matrix.
D(1, 1) = 2.0 * X(1);
D(1, 2) = 2.0 * X(2);
D(2, 1) = Pow(M_E, X(1));
D(2, 2) = 1.0;
return Standard_True;
}
virtual Standard_Boolean Values(const math_Vector& X, math_Vector& F, math_Matrix& D)
{
Value(X, F);
Derivatives(X, D);
return Standard_True;
}
private:
};
void test()
{
MyFunctionSet aFunctionSet;
math_FunctionSetRoot aSolver(aFunctionSet);
math_Vector aStartingPoint(1, 2);
// 1. (1.0, 1.0)
aStartingPoint(1) = 1.0;
aStartingPoint(2) = 1.0;
aSolver.Perform(aFunctionSet, aStartingPoint);
if (aSolver.IsDone())
{
aSolver.Dump(std::cout);
}
// 2. (1.0, -1.0)
aStartingPoint(1) = 1.0;
aStartingPoint(2) = -1.0;
aSolver.Perform(aFunctionSet, aStartingPoint);
if (aSolver.IsDone())
{
aSolver.Dump(std::cout);
}
}
int main(int argc, char* argv[])
{
test();
return 0;
}
上述代碼先定義了帶有一階偏導數的非線性方程組類:MyFunctionSet,因為有兩個變量及兩個方程,再分別實現計算方程值及偏導數的虛函數。
然后使用類math_FunctionSetRoot來對方程組進行求解,求解的結果如下圖所示:
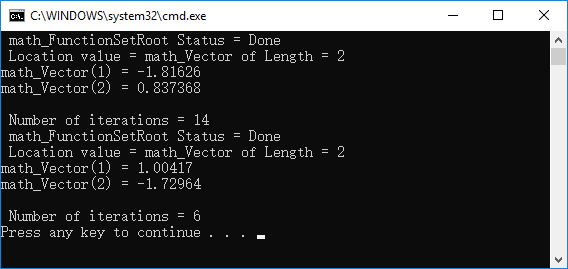
圖4 非線性方程組求解結果
由圖3可知,兩個曲線相交有兩個交點,但是使用類math_FunctionSetRoot一次只能計算一個解。從圖4的計算結果還可以看出,初值的選擇對解的影響很大,既影響計算結果,也影響迭代次數。
5.Conclusion
綜上所述,OpenCASCADE的math工具箱中提供了方程組的定義、求解功能。其中對非線性方程組求解使用的是Newton迭代法,所以要求方程組必須實現計算一階偏導數的虛函數,即計算Jacobi矩陣。
從OpenCASCADE類圖中可以看出,方程組定義類用在了很多地方,所以理解上述對方程組的定義及解的用法,對其他使用這個派生類的地方更容易其源碼。
6.References
- 同濟大學數學教研室. 高等數學 第四版. 高等教育出版社. 2004
- 易大義, 沈云寶, 李有法. 計算方法. 浙江大學出版社. 2002
為了方便大家在移動端也能看到我的博文和討論交流,現已注冊微信公眾號,歡迎大家掃描下方二維碼關注。
