Surface Normal Vector in OpenCascade
eryar@163.com
摘要Abstract:表面上某一點的法向量(Normal Vector)指的是在該點處與表面垂直的方向。對于平面,其上各點的法向是一樣的,統一為這個平面的法向。對于曲面,各點具有不同的法向量。幾何對象的法向量定義了它在空間中的方向,法向量是在進行光照處理時的重要參數。所以在顯示造型算法離散曲面后的網格時,設置正確的法向量對場景的光照、光線追蹤效果有直接影響。本文結合OpenCascade中代碼,對其法向量的計算方法進行分析,稍加修改即可用到實際的程序中。
關鍵字Key Words:OpenCascade, Normal Vector, Mesh Normal, OpenSceneGraph,
一、引言 Introduction
表面上某一點的法向量(Normal Vector)指的是在該點處與表面垂直的方向。對于平面,其上各點的法向是一樣的,統一為這個平面的法向。對于曲面,因為它在計算機圖形中是由許多片小平面的多邊形逼近來表示的,所以每個頂點的法向量都不一樣。因此,曲面上每個點的法向量計算就可以根據不同的應用有不同的算法,則最后的顯示效果也是不同的。幾何對象的法向量定義了它在空間中的方向,法向量是在進行光照處理時的重要參數。因為法向量決定了該如何計算光照,決定了該點能夠吸收多少光照。
OpenGL有很大的靈活性,它只提供賦予當前頂點法向量的函數,并不在內部具體計算其法向量,這個值由編程者自己根據需要設置。盡管法向量并不需要指定為單位向量,但是如果所有表面法向量都使用單位法向量可減少計算量。使用下列命令可自動將所有非單位法向量單位化:glEnable(GL_NORMALIZE),該命令也會對那些經過縮放或錯切等幾何變換的表面向量進行規范化。另一可用選項是指定一個法向量列表,與頂點數組混合使用。
在很多應用程序中網格上的各頂點都需要一個表面法向量,它的用途很廣泛:
l 計算光照;
l 背面剔除;
l 模擬粒子系統在表面的“彈跳”效果;
l 對只需要正面而加速碰撞檢測;
通常我們在繪制幾何體時都會指定法向量。當得到一個模型本身沒有法向量時,則有必要通過現有的數據生成。通常表面法向量可能保存于三角形級或頂點級,其中的一個技巧就是平均相鄰三角形的表面法向量,并將結果規范化。一般可以這樣假設三角形的頂點按逆時針排列,通過叉乘就可以得到外表面的法向量了。當然有些有情況下,頂點的順序是未知且比較混亂的,這樣就比較麻煩了。這個筆者也沒有仔細深入研究,推薦讀者看一下《計算非固定結構序列的多邊形的頂點法線》這篇論文。通過平均三角形法向量求得頂點法向量是一種經驗性的方法,不具有通用性,雖然很多情況下可以正確地工作,但有些情況下還是無法正常使用的。(以上內容摘自《OpenSceneGraph三維渲染引擎編程指南》)
二、計算法向量 Finding Surface Normal Vectors
OpenGL并不能自動計算幾何對象的法向量,而只能由用戶顯式指定。法向量的計算是一個純粹的幾何和數學問題,這里只簡略地區分了幾種情況。
2.1 計算平面的法向量
首先,講述平面法向量的計算方法。在平面內,有兩條相交的線段,假設其中一條為矢量W,另一條為矢量V,且平面法向量為N。如圖2.1所示,則平面法向量就等于兩個矢量的叉積(遵循右手法則),即N=W x V。
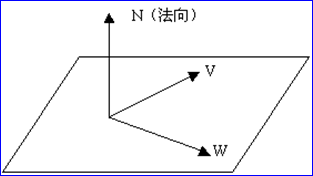
Figure 2.1 Normal Vector of Plane
比如計算一個三角形的法向就可以用它的三個頂點來計算,如圖2.2所示:
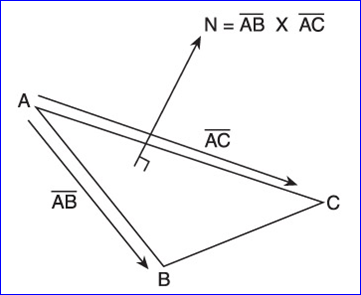
Figure 2.2 Finding the normal vector of a triangle
2.2 計算解析曲面的法向量
解析曲面是由數學方程描述的平滑的、可微曲面。在OpenCascade中曲面是由Geom_Surface來用參數u, v來表示的,相當于曲面的數學方程,是曲面的精確表示。通過計算曲面上一點u,v對應的一次微分即可得到曲面在該點處的切線,如下圖所示:

Figure 2.3 Tangents on a surface
關于參數u,v表示的Bezier曲面的微分計算方法如下所示:
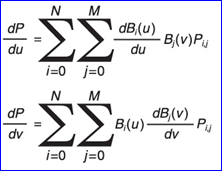
若需要計算參數對應點處的法向量,還需要對這兩個切向量進行叉乘即可,計算方法如下所示:

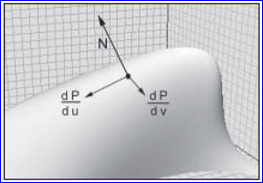
Figure 2.4 Normal on a surface
2.3 計算多邊形的法向量
在OpenGL中,這種情況占了大多數。求平均多邊形的法向量,利用不在同一直線上的多邊形三個頂點v1, v2, v3,則兩個矢量的叉積((v2 - v1)x(v3 - v1))垂直于多邊形,即為該多邊形的法向量,計算后需要經過規范化處理。
對于求多邊形網格上各頂點上的法向量,由于每個頂點同時位于幾個不同的多邊形邊界上,則需要求出周圍幾個多邊形的法向量,然后做加權平均。一般來說,可以使用每個多邊形的面積做為加權的權值。
如下圖所示,曲面頂點P的法向就等于其相鄰的四個平面的法向平均值:
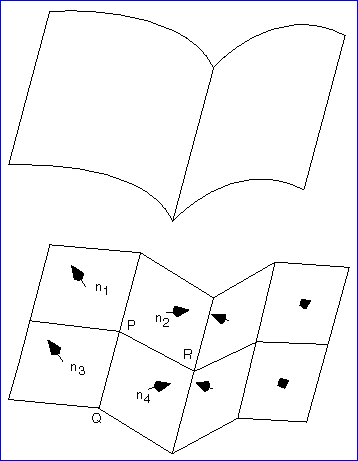
Figure 2. 曲面頂點的平均法向計算
注:當計算多邊形網格表示的曲面時,最好是使用平均法向的方法來計算。當曲面是用參數方程來表示時,就可以用求微分和叉乘的方法來直接計算法向量,不再需要使用平均法向了。
三、程序實現 Demo Code
3.1 OpenCascade中曲面法向量的計算 Compute normal in OpenCascade
在OpenCascade中將形狀數據保存為STL格式時就涉及到了將形狀三角剖分及其法向量的計算實現。其計算方法如上所述,也是分成三種方式:
l 參數方程表示的曲面;
l 平面;
l 網格;
將其代碼列出如下:
//function computes normals for surface
static void Normal(const TopoDS_Face& aFace,
Poly_Connect& pc,
TColgp_Array1OfDir& Nor)
{
const Handle(Poly_Triangulation)& T = pc.Triangulation();
BRepAdaptor_Surface S;
Standard_Boolean hasUV = T->HasUVNodes();
Standard_Integer i;
TopLoc_Location l;
Handle(Geom_Surface) GS = BRep_Tool::Surface(aFace, l);
if (hasUV && !GS.IsNull()) {
Standard_Boolean OK = Standard_True;
gp_Vec D1U,D1V;
gp_Vec D2U,D2V,D2UV;
gp_Pnt P;
Standard_Real U, V;
CSLib_DerivativeStatus Status;
CSLib_NormalStatus NStat;
S.Initialize(aFace, Standard_False);
const TColgp_Array1OfPnt2d& UVNodes = T->UVNodes();
if (!S.GetType() == GeomAbs_Plane) {
for (i = UVNodes.Lower(); i <= UVNodes.Upper(); i++) {
U = UVNodes(i).X();
V = UVNodes(i).Y();
S.D1(U,V,P,D1U,D1V);
CSLib::Normal(D1U,D1V,Precision::Angular(),Status,Nor(i));
if (Status != CSLib_Done) {
S.D2(U,V,P,D1U,D1V,D2U,D2V,D2UV);
CSLib::Normal(D1U,D1V,D2U,D2V,D2UV,Precision::Angular(),OK,NStat,Nor(i));
}
if (aFace.Orientation() == TopAbs_REVERSED) (Nor(i)).Reverse();
}
}
else {
gp_Dir NPlane;
U = UVNodes(UVNodes.Lower()).X();
V = UVNodes(UVNodes.Lower()).Y();
S.D1(U,V,P,D1U,D1V);
CSLib::Normal(D1U,D1V,Precision::Angular(),Status,NPlane);
if (Status != CSLib_Done) {
S.D2(U,V,P,D1U,D1V,D2U,D2V,D2UV);
CSLib::Normal(D1U,D1V,D2U,D2V,D2UV,Precision::Angular(),OK,NStat,NPlane);
}
if (aFace.Orientation() == TopAbs_REVERSED) NPlane.Reverse();
Nor.Init(NPlane);
}
}
else {
const TColgp_Array1OfPnt& Nodes = T->Nodes();
Standard_Integer n[3];
const Poly_Array1OfTriangle& triangles = T->Triangles();
for (i = Nodes.Lower(); i <= Nodes.Upper(); i++) {
gp_XYZ eqPlan(0, 0, 0);
for (pc.Initialize(i); pc.More(); pc.Next()) {
triangles(pc.Value()).Get(n[0], n[1], n[2]);
gp_XYZ v1(Nodes(n[1]).Coord()-Nodes(n[0]).Coord());
gp_XYZ v2(Nodes(n[2]).Coord()-Nodes(n[1]).Coord());
eqPlan += (v1^v2).Normalized();
}
Nor(i) = gp_Dir(eqPlan);
if (aFace.Orientation() == TopAbs_REVERSED) (Nor(i)).Reverse();
}
}
}
如果是參數方程表示的曲面,若不是平面,則根據切線的叉乘來計算各頂點處的法向量;若是平面,則只計算一個頂點處理的法向量,減少計算量。 若是離散后的網格面,則根據三角形的法向量的計算方法來計算每個頂點處的法向量。
3.2 OpenSceneGraph中網格曲面的法向量計算 Compute normal in OpenSceneGraph
生成頂點法向量(osgUtil::SmoothingVisitor)類繼承自osg::NodeVisitor類,采用Visitor模式,遍歷場景中的幾何體,生成頂點法向量。osgUtil::SmoothingVisitor的使用很方便。對算法實現感興趣的讀者可以結合源程序來理解研究。
四、結論 Conclusion
OpenCascascade中有曲面的參數表示,所以對這類曲面可以得用參數方程計算出曲面上的頂點的準確法向量。對于沒有參數表示的網格曲面,可以用平均法向量的方法來計算出一個法向量。
OpenSceneGraph中也有快速計算網格曲面法向量的類osgUtil::SmoothingVisitor。
五、參考資料 References
1. Kelly Dempski, Focus on Curves and Surfaces, Premier Press, 2003
2. 王銳,錢學雷,OpenSceneGraph三維渲染引擎設計與實踐,清華大學出版社
3. 肖鵬,劉更代,徐明亮,OpenSceneGraph三維渲染引擎編程指南,清華大學出版社