Intersection between a 2d line and a conic in OpenCASCADE
eryar@163.com
Abstract. OpenCASCADE provides the algorithm to implementation of the analytical intersection between a 2d line and another conic curve. The conic is defined by its implicit quadaratic equation, so the intersection problem is become a polynomial roots finding problem. The paper focus on the 2d line intersection another conic algorithm implementation.
Key Words. 2d line intersection, conic
1.Introduction
高中的時候學習了直線Line、圓Circle、圓錐曲線Conic(橢圓Ellipse、雙曲線Hyperbola和拋物線parabola)等二維曲線的方程及特性,也可以對他們之間的相交情況進行計算。如何編程實現直線與任意圓錐曲線相交呢?本文通過對OpenCASCADE中二維直線與圓錐曲線相交代碼的分析來理解其實現原理。
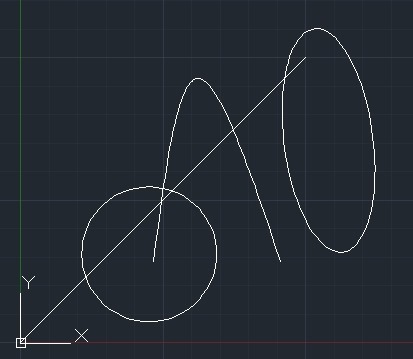
Figure 1. 直線與圓錐曲線相交
對于二維曲線知識的學習又把思緒拉回到高中年代,翻開泛黃的課本,遙想那個青澀時候,對于《數學》的學習也是停留在解題上,沒有理解,更別說應用了。有人說數學、英語和代碼是當今的世界語言,都可以進行思想的交流。數學本來就是描述現實世界規律的精妙語言,但我終究是個俗人,更崇拜能應用數學創建價值的人,如OpenCASCADE的開發者們。
2.Conic Implicit Equation
圓錐曲線一般的代數表示方法為:
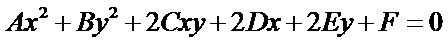
OpenCASCADE中使用類IntAna2d_Conic來表示圓錐曲線的代數方程。并提供了將二維曲線(直線、圓、橢圓、拋物線、雙曲線)轉換成代數方程的方法,相關代碼如下所示:
IntAna2d_Conic::IntAna2d_Conic (const gp_Lin2d& L) {
a = 0.0;
b = 0.0;
c = 0.0;
L.Coefficients(d,e,f);
f = 2*f;
}
IntAna2d_Conic::IntAna2d_Conic (const gp_Circ2d& C) {
C.Coefficients(a,b,c,d,e,f);
}
IntAna2d_Conic::IntAna2d_Conic (const gp_Elips2d& E) {
E.Coefficients(a,b,c,d,e,f);
}
IntAna2d_Conic::IntAna2d_Conic (const gp_Parab2d& P) {
P.Coefficients(a,b,c,d,e,f);
}
IntAna2d_Conic::IntAna2d_Conic (const gp_Hypr2d& H) {
H.Coefficients(a,b,c,d,e,f);
}
3.Intersection Implementation
當對直線和圓錐曲線進行求交時,先得到了直線的一般式方程和圓錐曲線的一般式方程,將它們聯立成方程組如下所示:
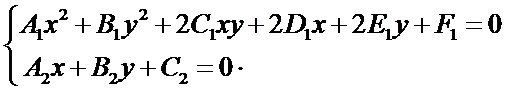
是一個二元二次方程組。通過直線的參數表示法,將上述二元二次方程組轉換成一元二次方程,再對這個方程進行求解。設直線l經過點P0(x0,y0),v=(a, b)是它的一個方向向量。P(x,y)是直線上任意一點,則向量P0P與v共線。根據向量共線的充要條件,存在唯一實數t,使:
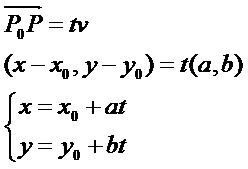
將直線的一般式化為參數式為:
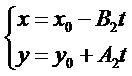
將直線的參數式代入圓錐曲線的一般式得到:
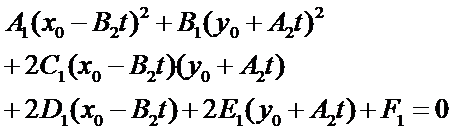
整理上述方程得:
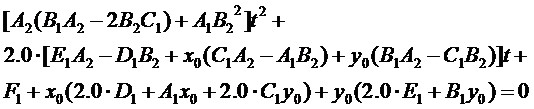
得到各次系數后,就可以用Newton法來解這個一元二次方程了。OpenCASCADE中的實現代碼如下所示:
void IntAna2d_AnaIntersection::Perform (const gp_Lin2d& L,
const IntAna2d_Conic& Conic)
{
Standard_Real A,B,C,D,E,F;
Standard_Real px0,px1,px2;
Standard_Real DR_A,DR_B,DR_C,X0,Y0;
Standard_Integer i;
Standard_Real tx,ty,S;
done = Standard_False;
nbp = 0;
para = Standard_False;
iden = Standard_False;
Conic.Coefficients(A,B,C,D,E,F);
L.Coefficients(DR_A,DR_B,DR_C);
X0=L.Location().X();
Y0=L.Location().Y();
// Parametre: L
// X = Xo - L DR_B et Y = Yo + L DR_A
px0=F + X0*(D+D + A*X0 + 2.0*C*Y0) + Y0*(E+E + B*Y0);
px1=2.0*(E*DR_A - D*DR_B + X0*(C*DR_A - A*DR_B) + Y0*(B*DR_A - C*DR_B));
px2=DR_A*(B*DR_A - 2.0*C*DR_B) + A*(DR_B*DR_B);
MyDirectPolynomialRoots Sol(px2,px1,px0);
if(!Sol.IsDone()) {
done=Standard_False;
return;
}
else {
if(Sol.InfiniteRoots()) {
iden=Standard_True;
done=Standard_True;
return;
}
nbp=Sol.NbSolutions();
for(i=1;i<=nbp;i++) {
S=Sol.Value(i);
tx=X0 - S*DR_B;
ty=Y0 + S*DR_A;
lpnt[i-1].SetValue(tx,ty,S);
}
Traitement_Points_Confondus(nbp,lpnt);
}
done=Standard_True;
}
從上述源碼可知,OpenCASCADE使用了直線的參數式來將直線與圓錐曲線的求交表示成一元二次方程,再使用Newton法來對方程進行求解。 其中變量px0、px1、px2分別表示一元二次方程的零次、一次和二次項的系數。
4.Conclusion
通過圓錐曲線的一般式和直線的參數式將直線與圓錐曲線相交問題變成一個一元二次方程的求根問題,再通過方程求根的Newton法來對一元二次方程進行求解。
5.References
1. 人民教育出版社中學數學室. 數學第二冊上. 人民教育出版社. 2000
2. 易大義, 沈云寶, 李有法. 計算方法. 浙江大學出版社. 2002
3. 李原, 張開富, 余劍峰. 計算機輔助幾何設計技術及應用. 西北工業大學出版社. 2007
4. 丘維聲. 解析幾何. 北京大學出版社. 1996