OpenCASCADE 3 Planes Intersection
eryar@163.com
Abstract. OpenCASCADE provides the algorithm to search the intersection point between 3 planes. If two of the planes are parallel or identical, will get no result.
Key Words. Plane Intersection
1.Introduction
由《高等數學》可知,如果一非零向量垂直于一平面,這向量就叫做該平面的法向量。平面上的任一向量均與該平面的法向量垂直。即平面上任一向量與法向量的點乘為0.
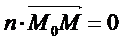
其中n為平面的法向量,M0M為平面上任兩點表示的向量。此式是平面的點法式方程。
由于平面的點法式方程是x,y,z的一次方程,而任一平面都可以用它上面的一點及法向量來確定,所以任一平面都可以用三元一次方程來表示。
Ax+By+Cz+D=0
其中x,y,z的系數就是該平面的一個法向量,即n={A,B,C}。上式就是平面的一般方程。設三個平面的方程分別為:
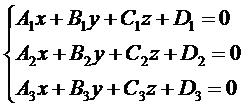
上述三個平面恰交于一點的充分必要條件是方程組有唯一解,即它的系數行列式不等于零:
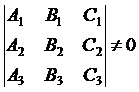
所以求三個平面交點的算法核心是對系數方程組的求解。
2.Algorithm
OpenCASCADE中也有計算三個平面交點的算法,使用類IntAna_Int3Pln。也是使用了直接的算法,即先根據平面的點法式方程計算出平面的一般式,再聯立方程組,最后使用高斯Gauss消元法進行求解。其核心代碼如下所示:
void IntAna_Int3Pln::Perform (const gp_Pln& P1, const gp_Pln& P2,
const gp_Pln& P3) {
done=Standard_False;
math_Matrix M(1,3,1,3);
math_Vector V(1,3);
P1.Coefficients(M(1,1),M(1,2),M(1,3),V(1));
P2.Coefficients(M(2,1),M(2,2),M(2,3),V(2));
P3.Coefficients(M(3,1),M(3,2),M(3,3),V(3));
math_Gauss Resol(M,gp::Resolution());
if (!Resol.IsDone()) {
empt=Standard_True;
}
else {
empt=Standard_False;
V=-V;
Resol.Solve(V);
pnt.SetCoord(V(1),V(2),V(3));
}
done=Standard_True;
}
算法首先根據平面的點向式數據計算出一般式的參數,使用的類gp_Pln的函數Coefficients(),代碼如下所示:
inline void gp_Pln::Coefficients (Standard_Real& A,
Standard_Real& B,
Standard_Real& C,
Standard_Real& D) const
{
const gp_Dir& dir = pos.Direction();
if (pos.Direct()) {
A = dir.X();
B = dir.Y();
C = dir.Z();
}
else {
A = -dir.X();
B = -dir.Y();
C = -dir.Z();
}
const gp_Pnt& P = pos.Location();
D = -(A * P.X() + B * P.Y() + C * P.Z());
}
根據平面的一般方程的定義可知,x,y,z的系數即為平面的法向,所以根據平面的法向量可以確定一般式的系數A、B、C。再代入平面上的任一點計算出D。
最后使用高斯Gauss消元法求解方程組得到三個平面的交點。
3. Conclusion
OpenCASCADE中對三個平面的交點的計算使用了直接的算法,即聯立方程組進行求解的方法。從中可以看出這些幾何問題在OpenCASCADE中的求解也都是數學的應用題。對方程組的求解,微分、積分等數值方法更是核心中的核心,所以OpenCASCADE將TKMath放在了基礎模塊。