Surface Normal Vector in OpenCascade
eryar@163.com
摘要Abstract:表面上某一點(diǎn)的法向量(Normal Vector)指的是在該點(diǎn)處與表面垂直的方向。對(duì)于平面,其上各點(diǎn)的法向是一樣的,統(tǒng)一為這個(gè)平面的法向。對(duì)于曲面,各點(diǎn)具有不同的法向量。幾何對(duì)象的法向量定義了它在空間中的方向,法向量是在進(jìn)行光照處理時(shí)的重要參數(shù)。所以在顯示造型算法離散曲面后的網(wǎng)格時(shí),設(shè)置正確的法向量對(duì)場(chǎng)景的光照、光線追蹤效果有直接影響。本文結(jié)合OpenCascade中代碼,對(duì)其法向量的計(jì)算方法進(jìn)行分析,稍加修改即可用到實(shí)際的程序中。
關(guān)鍵字Key Words:OpenCascade, Normal Vector, Mesh Normal, OpenSceneGraph,
一、引言 Introduction
表面上某一點(diǎn)的法向量(Normal Vector)指的是在該點(diǎn)處與表面垂直的方向。對(duì)于平面,其上各點(diǎn)的法向是一樣的,統(tǒng)一為這個(gè)平面的法向。對(duì)于曲面,因?yàn)樗谟?jì)算機(jī)圖形中是由許多片小平面的多邊形逼近來(lái)表示的,所以每個(gè)頂點(diǎn)的法向量都不一樣。因此,曲面上每個(gè)點(diǎn)的法向量計(jì)算就可以根據(jù)不同的應(yīng)用有不同的算法,則最后的顯示效果也是不同的。幾何對(duì)象的法向量定義了它在空間中的方向,法向量是在進(jìn)行光照處理時(shí)的重要參數(shù)。因?yàn)榉ㄏ蛄繘Q定了該如何計(jì)算光照,決定了該點(diǎn)能夠吸收多少光照。
OpenGL有很大的靈活性,它只提供賦予當(dāng)前頂點(diǎn)法向量的函數(shù),并不在內(nèi)部具體計(jì)算其法向量,這個(gè)值由編程者自己根據(jù)需要設(shè)置。盡管法向量并不需要指定為單位向量,但是如果所有表面法向量都使用單位法向量可減少計(jì)算量。使用下列命令可自動(dòng)將所有非單位法向量單位化:glEnable(GL_NORMALIZE),該命令也會(huì)對(duì)那些經(jīng)過(guò)縮放或錯(cuò)切等幾何變換的表面向量進(jìn)行規(guī)范化。另一可用選項(xiàng)是指定一個(gè)法向量列表,與頂點(diǎn)數(shù)組混合使用。
在很多應(yīng)用程序中網(wǎng)格上的各頂點(diǎn)都需要一個(gè)表面法向量,它的用途很廣泛:
l 計(jì)算光照;
l 背面剔除;
l 模擬粒子系統(tǒng)在表面的“彈跳”效果;
l 對(duì)只需要正面而加速碰撞檢測(cè);
通常我們?cè)诶L制幾何體時(shí)都會(huì)指定法向量。當(dāng)?shù)玫揭粋€(gè)模型本身沒(méi)有法向量時(shí),則有必要通過(guò)現(xiàn)有的數(shù)據(jù)生成。通常表面法向量可能保存于三角形級(jí)或頂點(diǎn)級(jí),其中的一個(gè)技巧就是平均相鄰三角形的表面法向量,并將結(jié)果規(guī)范化。一般可以這樣假設(shè)三角形的頂點(diǎn)按逆時(shí)針排列,通過(guò)叉乘就可以得到外表面的法向量了。當(dāng)然有些有情況下,頂點(diǎn)的順序是未知且比較混亂的,這樣就比較麻煩了。這個(gè)筆者也沒(méi)有仔細(xì)深入研究,推薦讀者看一下《計(jì)算非固定結(jié)構(gòu)序列的多邊形的頂點(diǎn)法線》這篇論文。通過(guò)平均三角形法向量求得頂點(diǎn)法向量是一種經(jīng)驗(yàn)性的方法,不具有通用性,雖然很多情況下可以正確地工作,但有些情況下還是無(wú)法正常使用的。(以上內(nèi)容摘自《OpenSceneGraph三維渲染引擎編程指南》)
二、計(jì)算法向量 Finding Surface Normal Vectors
OpenGL并不能自動(dòng)計(jì)算幾何對(duì)象的法向量,而只能由用戶顯式指定。法向量的計(jì)算是一個(gè)純粹的幾何和數(shù)學(xué)問(wèn)題,這里只簡(jiǎn)略地區(qū)分了幾種情況。
2.1 計(jì)算平面的法向量
首先,講述平面法向量的計(jì)算方法。在平面內(nèi),有兩條相交的線段,假設(shè)其中一條為矢量W,另一條為矢量V,且平面法向量為N。如圖2.1所示,則平面法向量就等于兩個(gè)矢量的叉積(遵循右手法則),即N=W x V。
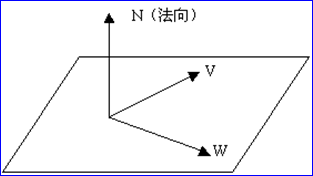
Figure 2.1 Normal Vector of Plane
比如計(jì)算一個(gè)三角形的法向就可以用它的三個(gè)頂點(diǎn)來(lái)計(jì)算,如圖2.2所示:
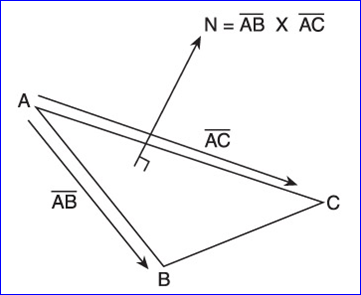
Figure 2.2 Finding the normal vector of a triangle
2.2 計(jì)算解析曲面的法向量
解析曲面是由數(shù)學(xué)方程描述的平滑的、可微曲面。在OpenCascade中曲面是由Geom_Surface來(lái)用參數(shù)u, v來(lái)表示的,相當(dāng)于曲面的數(shù)學(xué)方程,是曲面的精確表示。通過(guò)計(jì)算曲面上一點(diǎn)u,v對(duì)應(yīng)的一次微分即可得到曲面在該點(diǎn)處的切線,如下圖所示:

Figure 2.3 Tangents on a surface
關(guān)于參數(shù)u,v表示的Bezier曲面的微分計(jì)算方法如下所示:
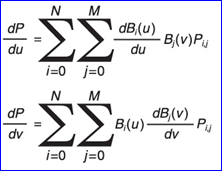
若需要計(jì)算參數(shù)對(duì)應(yīng)點(diǎn)處的法向量,還需要對(duì)這兩個(gè)切向量進(jìn)行叉乘即可,計(jì)算方法如下所示:

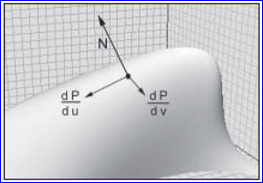
Figure 2.4 Normal on a surface
2.3 計(jì)算多邊形的法向量
在OpenGL中,這種情況占了大多數(shù)。求平均多邊形的法向量,利用不在同一直線上的多邊形三個(gè)頂點(diǎn)v1, v2, v3,則兩個(gè)矢量的叉積((v2 - v1)x(v3 - v1))垂直于多邊形,即為該多邊形的法向量,計(jì)算后需要經(jīng)過(guò)規(guī)范化處理。
對(duì)于求多邊形網(wǎng)格上各頂點(diǎn)上的法向量,由于每個(gè)頂點(diǎn)同時(shí)位于幾個(gè)不同的多邊形邊界上,則需要求出周圍幾個(gè)多邊形的法向量,然后做加權(quán)平均。一般來(lái)說(shuō),可以使用每個(gè)多邊形的面積做為加權(quán)的權(quán)值。
如下圖所示,曲面頂點(diǎn)P的法向就等于其相鄰的四個(gè)平面的法向平均值:
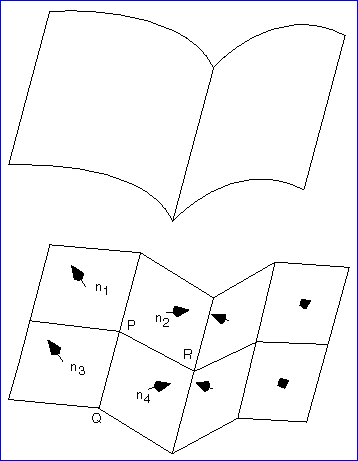
Figure 2. 曲面頂點(diǎn)的平均法向計(jì)算
注:當(dāng)計(jì)算多邊形網(wǎng)格表示的曲面時(shí),最好是使用平均法向的方法來(lái)計(jì)算。當(dāng)曲面是用參數(shù)方程來(lái)表示時(shí),就可以用求微分和叉乘的方法來(lái)直接計(jì)算法向量,不再需要使用平均法向了。
三、程序?qū)崿F(xiàn) Demo Code
3.1 OpenCascade中曲面法向量的計(jì)算 Compute normal in OpenCascade
在OpenCascade中將形狀數(shù)據(jù)保存為STL格式時(shí)就涉及到了將形狀三角剖分及其法向量的計(jì)算實(shí)現(xiàn)。其計(jì)算方法如上所述,也是分成三種方式:
l 參數(shù)方程表示的曲面;
l 平面;
l 網(wǎng)格;
將其代碼列出如下:
//function computes normals for surface
static void Normal(const TopoDS_Face& aFace,
Poly_Connect& pc,
TColgp_Array1OfDir& Nor)
{
const Handle(Poly_Triangulation)& T = pc.Triangulation();
BRepAdaptor_Surface S;
Standard_Boolean hasUV = T->HasUVNodes();
Standard_Integer i;
TopLoc_Location l;
Handle(Geom_Surface) GS = BRep_Tool::Surface(aFace, l);
if (hasUV && !GS.IsNull()) {
Standard_Boolean OK = Standard_True;
gp_Vec D1U,D1V;
gp_Vec D2U,D2V,D2UV;
gp_Pnt P;
Standard_Real U, V;
CSLib_DerivativeStatus Status;
CSLib_NormalStatus NStat;
S.Initialize(aFace, Standard_False);
const TColgp_Array1OfPnt2d& UVNodes = T->UVNodes();
if (!S.GetType() == GeomAbs_Plane) {
for (i = UVNodes.Lower(); i <= UVNodes.Upper(); i++) {
U = UVNodes(i).X();
V = UVNodes(i).Y();
S.D1(U,V,P,D1U,D1V);
CSLib::Normal(D1U,D1V,Precision::Angular(),Status,Nor(i));
if (Status != CSLib_Done) {
S.D2(U,V,P,D1U,D1V,D2U,D2V,D2UV);
CSLib::Normal(D1U,D1V,D2U,D2V,D2UV,Precision::Angular(),OK,NStat,Nor(i));
}
if (aFace.Orientation() == TopAbs_REVERSED) (Nor(i)).Reverse();
}
}
else {
gp_Dir NPlane;
U = UVNodes(UVNodes.Lower()).X();
V = UVNodes(UVNodes.Lower()).Y();
S.D1(U,V,P,D1U,D1V);
CSLib::Normal(D1U,D1V,Precision::Angular(),Status,NPlane);
if (Status != CSLib_Done) {
S.D2(U,V,P,D1U,D1V,D2U,D2V,D2UV);
CSLib::Normal(D1U,D1V,D2U,D2V,D2UV,Precision::Angular(),OK,NStat,NPlane);
}
if (aFace.Orientation() == TopAbs_REVERSED) NPlane.Reverse();
Nor.Init(NPlane);
}
}
else {
const TColgp_Array1OfPnt& Nodes = T->Nodes();
Standard_Integer n[3];
const Poly_Array1OfTriangle& triangles = T->Triangles();
for (i = Nodes.Lower(); i <= Nodes.Upper(); i++) {
gp_XYZ eqPlan(0, 0, 0);
for (pc.Initialize(i); pc.More(); pc.Next()) {
triangles(pc.Value()).Get(n[0], n[1], n[2]);
gp_XYZ v1(Nodes(n[1]).Coord()-Nodes(n[0]).Coord());
gp_XYZ v2(Nodes(n[2]).Coord()-Nodes(n[1]).Coord());
eqPlan += (v1^v2).Normalized();
}
Nor(i) = gp_Dir(eqPlan);
if (aFace.Orientation() == TopAbs_REVERSED) (Nor(i)).Reverse();
}
}
}
如果是參數(shù)方程表示的曲面,若不是平面,則根據(jù)切線的叉乘來(lái)計(jì)算各頂點(diǎn)處的法向量;若是平面,則只計(jì)算一個(gè)頂點(diǎn)處理的法向量,減少計(jì)算量。 若是離散后的網(wǎng)格面,則根據(jù)三角形的法向量的計(jì)算方法來(lái)計(jì)算每個(gè)頂點(diǎn)處的法向量。
3.2 OpenSceneGraph中網(wǎng)格曲面的法向量計(jì)算 Compute normal in OpenSceneGraph
生成頂點(diǎn)法向量(osgUtil::SmoothingVisitor)類繼承自osg::NodeVisitor類,采用Visitor模式,遍歷場(chǎng)景中的幾何體,生成頂點(diǎn)法向量。osgUtil::SmoothingVisitor的使用很方便。對(duì)算法實(shí)現(xiàn)感興趣的讀者可以結(jié)合源程序來(lái)理解研究。
四、結(jié)論 Conclusion
OpenCascascade中有曲面的參數(shù)表示,所以對(duì)這類曲面可以得用參數(shù)方程計(jì)算出曲面上的頂點(diǎn)的準(zhǔn)確法向量。對(duì)于沒(méi)有參數(shù)表示的網(wǎng)格曲面,可以用平均法向量的方法來(lái)計(jì)算出一個(gè)法向量。
OpenSceneGraph中也有快速計(jì)算網(wǎng)格曲面法向量的類osgUtil::SmoothingVisitor。
五、參考資料 References
1. Kelly Dempski, Focus on Curves and Surfaces, Premier Press, 2003
2. 王銳,錢學(xué)雷,OpenSceneGraph三維渲染引擎設(shè)計(jì)與實(shí)踐,清華大學(xué)出版社
3. 肖鵬,劉更代,徐明亮,OpenSceneGraph三維渲染引擎編程指南,清華大學(xué)出版社