Convert BSpline Curve to Arc Spline in OpenCASCADE
eryar@163.com
Abstract. The paper based on OpenCASCADE algorithms to approximate the NURBS curve to arc spline. The method is most useful in numerical control to drive the cutter along straight line or circular paths. Or in the shipbuilding industry to manufacture section bar for cold frame bender.
Key Words. NURBS, Biarc approximation, arc spline,
1.Introduction
在數控加工CNC領域,通常需要用盡量少段數的圓弧和直線段來對曲線進行擬合���。有的數控繪圖機也只有直線和圓弧插補器,即只能繪制直線和圓弧�,所以也需要將自由曲線轉換成直線和圓弧來進行繪制�。在船舶制造方面�����,如肋骨冷彎機只有兩種狀態:彎和不彎���,也只能加工出直線和圓弧,所以也需要將曲面型材的彎曲信息轉換成肋骨冷彎機能加工的數據。如下圖所示為型材模型及其基線:

Figure 1. 型材模型及基線
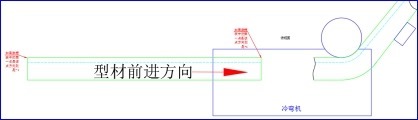
Figure 2. 肋骨冷彎機
如上圖所示,型材都是直線的���,通過彎曲加工出曲線效果。所以也需要將實際的自由曲線的型材數據轉換成圓弧樣條(直線和圓?。┍阌诩庸?����。國內外關于這方面的論文很多�,本文基于opencascade做了一個測試�����,opencascade平臺相關的數據結構完善�����,B樣條相關算法齊全,可以基于這個開源平臺做些開發�。
2.Algorithm
看了國內外的一些論文�����,對NURBS曲線進行圓弧樣條擬合的大概思路都是一個先對NURBS曲線離散的過程。一個極端情況就是生成NURBS曲線的顯示數據���,即多段線來逼近。多段線對于有的機器設備(CNC)而言�,加工不便�,所以提出盡量使用少的圓弧和直線段來逼近NURBS曲線這種問題�。
總的思路是先將NURBS曲線離散成多段線,或將NURBS轉換成分段Bezier曲線,然后再用雙圓弧樣條曲線來進行擬合。
3.Polygon Approximation
將曲線離散成多段線的相關算法是個相對重要的算法���,因為可以用于對NURBS曲線的顯示。生成曲線顯示數據時也有用盡量少的多段線來逼近曲線的問題。所以可以先用生成曲線顯示數據的算法來對曲線進行離散化���。OpenCASCADE中取曲線上點的相關類都在包GCPnts中:
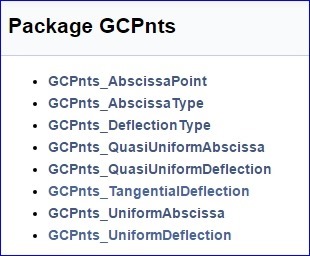
如類GCPnts_TangentialDeflection可以在滿足角度偏差和曲率偏差的條件下對曲線進行離散化���。根據文檔注釋可知:
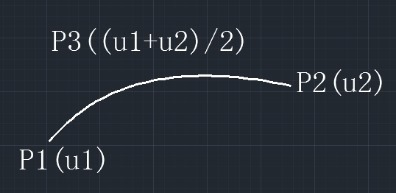

由上圖可知�,曲線離散的算法滿足條件為向量P1P3和P3P2之間的夾角和P1P2與P1P3之間的夾角分別滿足角度和曲率偏差。
如果對經過上述算法處理過的曲線上相鄰兩個點�,根據切線來擬合一段圓弧�,這樣處理起來程序比用雙圓弧擬合要簡單���,對于尖點的處理也很方便���。
過樣條曲線上相鄰兩個節點�����,且在節點處都切于樣條曲線的圓弧一般是不存在的���,但卻可以決定一圓弧使得在節點處兩對切線間的夾角相等�,這種方法稱為平均切線法���。故結合樣條曲線離散算法和平均切線法�,可以將樣條曲線轉換成直線和圓弧來逼近表示的圓弧樣條曲線。直線的情況就是相鄰兩個節點處的切線之間的夾角小于一定的偏差���,則認為是直線,其他情況都認為是圓弧�。
4.Arc Spline Fitting
根據上述原理使用OpenCascade編寫程序�,OpenCascade在NURBS方面的算法還是很全面的���,如計算NURBS曲線曲面上的點或切線���,或任意階導數等等�����。也有關于圓弧、線段等全面的數據結構���,所以借助OpenCascade這個平臺,可以快速實現一些想法���。
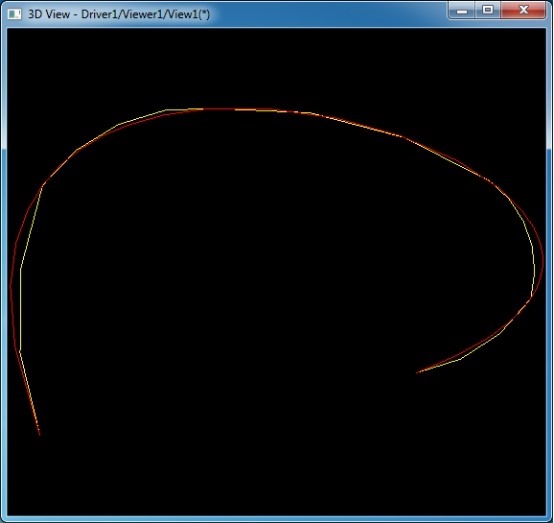
上圖所示為當精度為0.5時B樣條曲線轉換成圓弧樣條曲線的結果。其中紅色曲線為B樣條曲線�,黃色為圓弧樣條���。
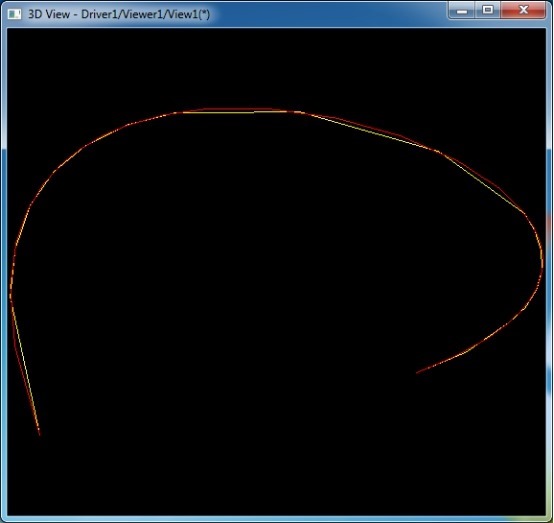
當精度為0.1時得到的圓弧樣條�����。
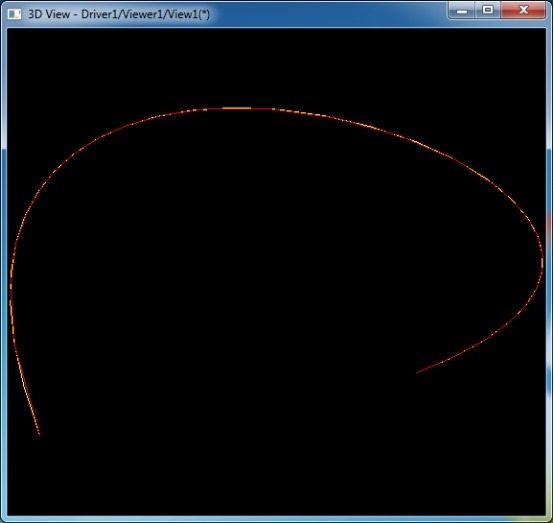
當精度為0.01時得到的圓弧樣條���。由圖可知�,圓弧樣條與B樣條基本重合�。
5.Conclusion
綜上所述,當離散精度越高時�����,得到的圓弧樣條越逼近原始的B樣條�,但是圓弧和直線段的數量也會越多。
使用上述算法實現程序簡單���,避免了雙圓弧擬合的一些復雜計算。
OpenCascade中有完善的NURBS相關算法及常見的幾何曲線曲面的數據結構���,所以借助這個平臺,可以快速驗證一些想法�����。
6.References
1.Les A. Piegl, Wayne Tiller. Biarc approximation of NURBS curves.
2.盧建彪�����,雍俊海. 二次Bezier曲線的雙圓弧樣條插值二分算法.
3.何援軍. 計算機圖形學. 機械工業出版社. 2010