OpenCASCADE Interpolations and Approximations
eryar@163.com
Abstract. In modeling, it is often required to approximate or interpolate points to curves and surfaces. In interpolation, the process is complete when the curve or surface passes through all the points; in approximation, when it is as close to these points as possible. The paper is the translation of the OpenCASCADE Modeling Data user guide.
Key Words. Interpolation, Approximation, Fitting
1.Introduction
在幾何造型中,經常會需要根據點去擬合(插值Interpolation或逼近Approximation)曲線曲面。插值要求擬合所得的曲線或曲面必須通過所有擬合點;而逼近要求擬合所得曲線或曲面盡可能地靠近全部擬合點。OpenCASCADE中提供了曲線曲面擬合的功能有:
v 對二維點進行二維B樣條或Bezier曲線插值;
v 對二維點進行二維B樣條或Bezier曲線逼近;
v 對三維點進行三維B樣條或Bezier曲線或B樣條曲面插值;
v 對三維點進行三維B樣條或Bezier曲線或B樣條曲面逼近;
程序中使用擬合功能有兩種方式:
v 使用高級功能:提供簡單的方法調用來獲得擬合結果;
v 使用低級功能:專為想對擬合有更多控制的用戶設計;
插值和逼近也是數值分析或計算方法中的主要內容。用B樣條作為插值或逼近函數是數值分析中的一個具體方法。通過對OpenCASCADE中插值和逼近算法的學習,加深對一些算法,如最小二乘法,多元函數求極值等數學知識的理解。
本文主要是對OpenCASCADE的文檔Modeling Data 中的插值和逼近部分進行翻譯,并給出了使用其低級功能具體的代碼示例。
2.Analysis of a set of points
包GProp中的類PEquation提供了對點集、點云數據進行分析的功能,可以用來驗證在給定的精度范圍內是否重合、共線或共面等,如果檢測結果是,那么算法將計算出這些點的重合點、線或面。如果檢測結果不是,則算法會計算出點集或點云的包圍盒。
3.Basic Interpolation and Approximation
包Geom2dAPI和GeomAPI提供了擬合(逼近和插值)簡單的方法。
v 2D Interpolation: 類Geom2dAPI_Interpolate可以用于生成一條通過一系列點的二維B樣條曲線。如果需要,還可以設置點相應的切矢及參數來對插值曲線做進一步的約束。
v 3D Interpolation: 類GeomAPI_Interpolate可以用于生成一條通過一系列點的三維B樣條曲線。如果需要,還可以設置點相應的切矢及參數來對插值曲線做進一步的約束。因為是高級功能,所以需要很少的代碼就可以得到插值曲線,用法如下:
GeomAPI_Interpolate Interp(Points);
Handle_Geom_BSplineCurve C = Interp.Curve()
v 2D Approximation: 類Geom2dAPI_PointsToBSpline可以用于生成逼近一系列點的二維B樣條曲線。你需要定義曲線次數范圍,連續性和容差。容差值只是用來檢查逼近點之間是不是有重合點,或者切矢是否太小。逼近曲線將會是C2連續或2次曲線,當有切矢約束時,將會得到C1連續的曲線。
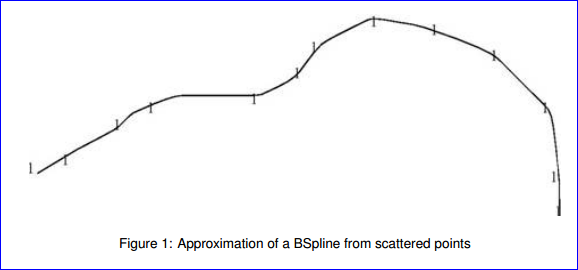
v 3D Approximation:類GeomAPI_PointsToBSpline可以用于生成逼近一系列點的三維B樣條曲線。你需要定義曲線次數范圍,連續性和容差。容差值只是用來檢查逼近點之間是不是有重合點,或者切矢是否太小。逼近曲線將會是C2連續或2次曲線,當有切矢約束時,將會得到C1連續的曲線。類的用法如下:
GeomAPI_PointsToBSpline Approx(Points, DegMin, DegMax, Continutity, Tol);
Handle_Geom_BSplineCurve K = Approx.Curve()
v Surface Approximation:類GeomAPI_PointsToBSplineSurface可以用于根據點集擬合B樣條曲面。
4.Advanced Approximation
包AppDef和AppParCurves提供了低級的功能,允許對擬合有更多地控制。低級功能提供了如下函數接口API:
v 定義擬合切矢的規則,這些切矢有原點和極值;
v 根據各自參數平行地擬合一系列曲線;
v 光滑擬合:生成光順(faired curve)的曲線。
注:包AppDef和AppParCurves中通過宏定義實現了一種類似多態的功能,但是程序調試不方便,導致一些類名沒有看到聲明文件,對程序的理解造成一些不便。
4.1 Approximation by multiple point constraints
包AppDef中提供了低級工具用于對帶約束的點集進行Bezier或B樣條曲線擬合。其中的功能有:
v 定義一組約束點,使用類AppDef_MultiPointConstraint;
v 定義一組約束線,使用類AppDef_MultiLine;
v 擬合Bezier曲線,使用類AppDef_Compute;
v 擬合B樣條曲線,使用類AppDef_BSplineCompute;
v 定義變分標準Variational Criteria;
注:在類AppDef_Variational中可以看到Variational Optimization變分優化。對于工科出來的人來說,這些概念還真是有些陌生,還是學數學的人厲害!
其中類AppDef_MultiLine的用法也有點特別,通過文檔中的圖來理解下:
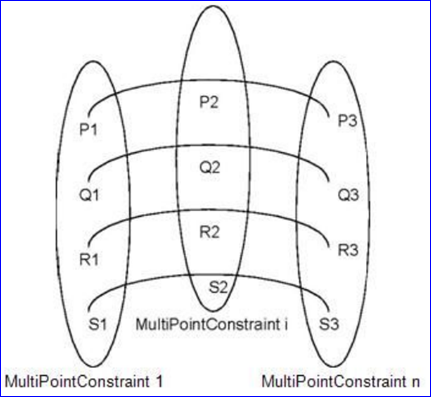
其中:Pi, Qi, Ri, ..., Si可以是二維點或三維點;
按組來定義,其中Pn, Qn, Rn, ..., Sn都是在類AppDef_MultiPointConstraint中定義;
P1, P2, .., Pn或Q, R,..., S的點系列用來擬合。
類AppDef_Compute用Bezier曲線來擬合點;
類AppDef_BSplineCompute用B樣條曲線來擬合點;
注:需要仔細理解AppDef_MultiPointConstraint和AppDef_MultiLine的用法。
4.2 Example: How to approximate a curve with low-level tools
使用低級功能的過程可分為如下幾步:
v 定義擬合點;
v 根據擬合點創建MultiLine;
v 使用AppDef_Compute或AppDef_BSplineCompute來擬合曲線;
下面給出使用低級功能的代碼示例:
/*
* Copyright (c) 2016 Shing Liu All Rights Reserved.
*
* File : main.cpp
* Author : Shing Liu(eryar@163.com)
* Date : 2016-03-17 21:00
* Version : OpenCASCADE6.9.0
*
* Description : test the low-level tools of approximation.
*/
#define WNT
#include <TColgp_Array1OfPnt.hxx>
#include <AppDef_MultiPointConstraint.hxx>
#include <AppDef_MultiLine.hxx>
#include <AppDef_Compute.hxx>
#include <AppDef_BSplineCompute.hxx>
#pragma comment(lib, "TKernel.lib")
#pragma comment(lib, "TKMath.lib")
#pragma comment(lib, "TKGeomBase.lib")
void testBezierApprox()
{
TColgp_Array1OfPnt aPoints(1, 3);
aPoints.SetValue(1, gp_Pnt(0.0, 0.0, 0.0));
aPoints.SetValue(2, gp_Pnt(1.0, 0.0, 0.0));
aPoints.SetValue(3, gp_Pnt(1.0, 1.0, 0.0));
AppDef_MultiLine aMultiLine(aPoints);
AppDef_Compute aBezierApprox(aMultiLine);
aBezierApprox.Value().Dump(std::cout);
}
void testBSplineApprox()
{
AppDef_MultiLine aMultiLine(3);
AppDef_MultiPointConstraint aMPC1(2, 0);
AppDef_MultiPointConstraint aMPC2(2, 0);
AppDef_MultiPointConstraint aMPC3(2, 0);
aMPC1.SetPoint(1, gp_Pnt(0.0, 0.0, 0.0));
aMPC1.SetPoint(2, gp_Pnt(0.0, 2.0, 0.0));
aMPC2.SetPoint(1, gp_Pnt(1.0, 0.0, 0.0));
aMPC2.SetPoint(2, gp_Pnt(1.0, 2.0, 0.0));
aMPC3.SetPoint(1, gp_Pnt(1.0, 1.0, 0.0));
aMPC3.SetPoint(2, gp_Pnt(1.0, 3.0, 1.0));
aMultiLine.SetValue(1, aMPC1);
aMultiLine.SetValue(2, aMPC2);
aMultiLine.SetValue(3, aMPC3);
AppDef_BSplineCompute aBSplineApprox(aMultiLine);
aBSplineApprox.Value().Dump(std::cout);
}
int main(int argc, char* argv[])
{
testBezierApprox();
testBSplineApprox();
return 0;
}
程序運行結果如下圖所示:
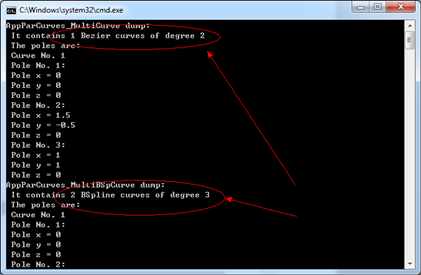
5.Conclusion
關于點的插值和逼近是《數據逼近》或《數值分析》或《計算方法》書中關注的內容。從文檔中可以看到包AppDef中的一些關鍵字:Gradient, BFGS, LeastSquare等,根據這些關鍵字可以看出OpenCASCADE中逼近使用的算法了。
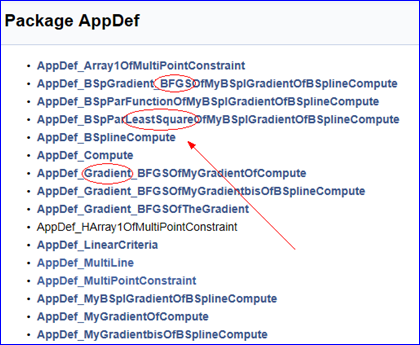
通過使用AppDef_MultiPointConstraint及AppDef_MultiLine等低級接口,來理解擬合數據點輸入及擬合結果的輸出。進而去學習BFGS、LeastSquare等數學理論工具在實際中的應用。對于多元函數,梯度及BFGS等概念還好接受,對于變分法優化之類理論已經超出了工科數學的范圍,不過結合實際去學習這些概念應該會更有效率。