OPEN CASCADE Gauss Least Square
eryar@163.com
Abstract. The least square can be used to solve a set of n linear equations of m unknowns(n >= m). The OPEN CASCADE class math_GaussLeastSquare implements the least square solution of the linear equations by using Gauss LU decomposition algorithm. The paper focus on the Least Square method to solve the linear equations.
Key Words. Least Square, LU Decomposition, Linear Equations
1.Introduction
最小二乘（Least Square）問題是一類特殊的無約束優(yōu)化問題，它在科學與工程計算中有十分重要的應用。最小二乘問題產(chǎn)生于數(shù)據(jù)擬合問題，它是一種基于觀測數(shù)據(jù)與模型數(shù)據(jù)之間的差的平方和最小來估計模型參數(shù)的方法。它最早由德國數(shù)學家高斯Gauss于1794年，在預測行星軌道時提出，當時高斯只有17歲，后來得到廣泛應用。
許多工程問題常常需要根據(jù)兩個變量的幾組實驗數(shù)值來找出這兩個變量的函數(shù)關系的近似表達式，通常把這樣得到的函數(shù)的近似表達式稱為經(jīng)驗公式。經(jīng)驗公式建立后就可以把生產(chǎn)或?qū)嶒炛兴e累的某些經(jīng)驗提高到理論上加以分析。
在幾何造型中常常需要對曲線和曲面進行擬合（插值和逼近），根據(jù)一些采樣點來擬合曲線曲面。逼近比插值更為困難。在插值問題中，只是根據(jù)采樣點來建立方程組，直接求解方程組即可得到結(jié)果，不需要進行容差檢查。而在逼近問題中，容差和采樣點一起作為輸入，一般預先不知道需要多少個控制點才能達到預期的精度，因此逼近一般都需要通過迭代來實現(xiàn)。通過最小二乘法即可實現(xiàn)達到精度要求的擬合結(jié)果，如OPEN CADCADE中的曲線曲面逼近就采用了最小二乘算法。
本文主要關注于最小二乘法求解線性方程組的原理及OPEN CASCADE中的實現(xiàn)和用法，為探索最小二乘法在OPEN CASCADE曲線曲面擬合方面的應用提前做些熱身準備。最小二乘問題涉及到非線性最優(yōu)化的相關知識，對多元函數(shù)的微積分有些要求，可以找出原來的《高等數(shù)學》或《數(shù)學分析》的課本復習下。本文關注的應用最小二乘法求解線性方程組問題只涉及到線性代數(shù)或矩陣相關的知識。
2.Principle
在羅家洪、方衛(wèi)東編著的《矩陣分析引論》一書中的2.5節(jié)點到子空間距離與最小二乘法，用歐氏空間的概念來表達最小二乘法，并給出最小二乘解所滿足的代數(shù)條件的證明過程。本文摘抄主要內(nèi)容對最小二乘法求解線性方程組的理解。
設已給不相容實系數(shù)線性方程組（即無解的線性方程組）：
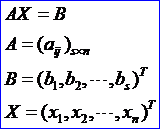
因為這方程組無解，設法找出一組數(shù)x1’, x2’, ..., xn’使平方偏差最小：
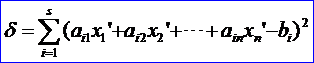
這組數(shù)稱為此方程組的最小二乘解，這一方法叫做最小二乘法。經(jīng)證明，最小二乘解所滿足的代數(shù)方程為：
它是一個線性方程組，系數(shù)矩陣為ATA，常數(shù)項為ATB。使用上述結(jié)論來解如下線性方程組：
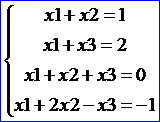
由于：
所以：
于是求得最小二乘解為：x1=17/6, x2=-13/6, x3=-4/6。
在OPEN CASCADE的數(shù)據(jù)工具集中TKMath，使用類math_GaussLeastSquare來利用最小二乘法來對線性方程組進行求解。其實現(xiàn)代碼如下所示：
math_GaussLeastSquare::math_GaussLeastSquare (const math_Matrix& A,
const Standard_Real MinPivot) :
LU(1, A.ColNumber(),
1, A.ColNumber()),
A2(1, A.ColNumber(),
1, A.RowNumber()),
Index(1, A.ColNumber()) {
A2 = A.Transposed();
LU.Multiply(A2, A);
Standard_Integer Error = LU_Decompose(LU, Index, D, MinPivot);
Done = (!Error) ? Standard_True : Standard_False;
}
void math_GaussLeastSquare::Solve(const math_Vector& B, math_Vector& X) const{
StdFail_NotDone_Raise_if(!Done, " ");
Standard_DimensionError_Raise_if((B.Length() != A2.ColNumber()) ||
(X.Length() != A2.RowNumber()), " ");
X.Multiply(A2, B);
LU_Solve(LU, Index, X);
return;
}
結(jié)合上述公式，再來理解這個代碼實現(xiàn)的思路還是很清晰的。
3.Code Example
OPEN CASCADE的TKMath工具集中提供了類math_GaussLeastSquare實現(xiàn)了使用高斯LU分解算法求m個未知數(shù)的n個線性方程組的最小二乘解，其中n>=m。下面給出使用類math_GaussLeastSquare對上述線性方程組進行求解的示例程序：
/*
* Copyright (c) 2015 Shing Liu All Rights Reserved.
*
* File : main.cpp
* Author : Shing Liu(eryar@163.com)
* Date : 2015-11-25 21:00
* Version : OpenCASCADE6.9.0
*
* Description : Test Gauss Least Square method to
* solve linear equations.
*/
#define WNT
#include <math_GaussLeastSquare.hxx>
#pragma comment(lib, "TKernel.lib")
#pragma comment(lib, "TKMath.lib")
void testLeastSquare(void)
{
math_Matrix A(1, 4, 1, 3);
math_Vector B(1, 4);
math_Vector X(1, 3);
A(1,1) = 1.0; A(1,2) = 1.0; A(1,3) = 0.0; B(1) = 1.0;
A(2,1) = 1.0; A(2,2) = 0.0; A(2,3) = 1.0; B(2) = 2.0;
A(3,1) = 1.0; A(3,2) = 1.0; A(3,3) = 1.0; B(3) = 0.0;
A(4,1) = 1.0; A(4,2) = 2.0; A(4,3) = -1.0; B(4) = -1.0;
math_GaussLeastSquare aSolver(A);
aSolver.Solve(B, X);
if (aSolver.IsDone())
{
std::cout << aSolver;
std::cout << X;
}
}
int main(int argc, char* argv[])
{
testLeastSquare();
return 0;
}
程序運行結(jié)果如下圖所示：
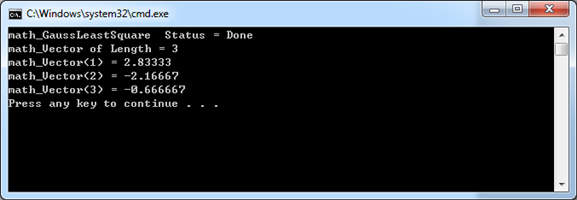
由上圖可知，計算結(jié)果吻合。
4.Conclusion
最小二乘法在系統(tǒng)理論中處理最小優(yōu)化問題時有重要應用，本文主要關注于線性方程組的最小二乘法求解，且對方程個數(shù)與未知數(shù)個數(shù)不要求相等。最小二乘法也是在我們學習高等數(shù)學的多元函數(shù)微分后，提出的一個實用的函數(shù)公式擬合方法。雖然本文所述的最小二乘法主要用于方程組的求解，但是OPEN CASCADE中曲線曲面的逼近也是采用了最小二乘法，這里最小二乘法就涉及到非線性最優(yōu)化的相關理論。
縱觀OPEN CASCADE的數(shù)學工具集TKMath中，大量地用到了非線性最優(yōu)化理論，如類math_BFGS就實現(xiàn)了Broyden-Fletcher-Goldfarb-Shanno（BFGS），用于計算多變量函數(shù)的最小值，類math_FRPR實現(xiàn)了Fletcher-Reeves-Polak-Ribiere算法。BFGS算法是擬牛頓方法，是解決無約束優(yōu)化問題既快又穩(wěn)定的算法。這些最優(yōu)化算法廣泛地用于OPEN CASCADE中曲線曲面擬合、光順及求交等算法中。所以有必要對最優(yōu)化方法，非線性最優(yōu)化理論等知識進行學習。掌握一些最優(yōu)化方法，不僅可以方便理解OPEN CASCADE中的核心關鍵算法，還可以將這些理論方法靈活應用在自己的程序中，提高軟件質(zhì)量。由于本人能力有限，先在這兒拋磚引玉，感興趣的讀者可以結(jié)合相關書籍對非線性最優(yōu)化理論進行學習，研究，應用，創(chuàng)新。
5.References
1. 同濟大學數(shù)學教研室. 高等數(shù)學. 高等教育出版社. 1996
2. 王仁宏. 李崇君. 朱春鋼. 計算幾何教程. 科學出版社. 2008
3. 羅家洪. 方衛(wèi)東. 矩陣分析引論. 華南理工大學出版社. 2006
4. 易大義. 陳道琦. 數(shù)值分析引論. 浙江大學出版社. 1998
5. 趙罡. 穆國旺. 王拉柱. 非均勻有理B樣條. 清華大學出版社. 2010
6. 王宜舉. 修乃華. 非線性最優(yōu)化理論與方法. 科學出版社. 2012