OPEN CASCADE Curve Continuity
eryar@163.com
Abstract. 設(shè)計(jì)一條復(fù)雜曲線時(shí),出于設(shè)計(jì)和制造上的考慮,常常通過(guò)多段曲線組合而成,這就需要解決曲線段之間如何實(shí)現(xiàn)光滑連接的問題。評(píng)價(jià)曲線間連接的光滑度的度量有兩種:參數(shù)連接性和幾何連續(xù)性。本文對(duì)這兩種連續(xù)性分別進(jìn)行介紹。
Key Words. Curve Continuity, Geometric Continuity, 參數(shù)連續(xù)性、幾何連續(xù)性
1.Introduction
在實(shí)際應(yīng)用中進(jìn)行復(fù)雜零件的幾何設(shè)計(jì)時(shí),通常我們用到的不僅僅是整個(gè)曲線,而是滿足一定的連續(xù)條件拼接而成的曲線段組成的組合曲線。關(guān)于連續(xù)條件有兩種不同的度量方法。一種是滿足于數(shù)學(xué)上嚴(yán)格定義的函數(shù)曲線可微性方法;別一種是滿足相對(duì)寬松的約束條件的幾何連續(xù)性方法。
本文對(duì)連續(xù)性的兩種度量方法進(jìn)行介紹,來(lái)理解參數(shù)連續(xù)性和幾何連續(xù)性。對(duì)連續(xù)性的概念有個(gè)認(rèn)識(shí)后,在使用OPEN CASCADE或其他幾何造型內(nèi)核時(shí),當(dāng)出現(xiàn)需要指定連續(xù)性的時(shí)候,不至于茫然無(wú)措。
2.Parametric Continuity
利用函數(shù)曲線的可微性,曲線在連接處具有直到n階連續(xù)導(dǎo)矢,即n次連續(xù)可微,這類光滑度稱之為Cn或n階參數(shù)連續(xù)性。下面給出參數(shù)連續(xù)性Parametric Continuity的定義:
參數(shù)曲線C(u)在u=u0處為k階參數(shù)連續(xù)(Ck連續(xù))的充要條件是:C(u)的每個(gè)分量在u=u0處Ck連續(xù),即

如果對(duì)所有的u∈[a,b],曲線C(u)均Ck連續(xù),則稱它為關(guān)于參數(shù)u的Ck連續(xù)曲線。在函數(shù)曲線里,可微性和光滑度是一致的,函數(shù)曲線是C1連續(xù),意味著具有連續(xù)的切矢;C2連續(xù)意味著不僅具有連續(xù)的切矢,還具有連續(xù)的曲率。由于曲線的參數(shù)選取并不唯一,同樣的曲線可以有不同的參數(shù)表示,而曲線的參數(shù)連續(xù)又與參數(shù)選取緊密相關(guān)。若參數(shù)變換前曲線為Ck連續(xù),但曲線的參數(shù)變換后可能不能在每一點(diǎn)處都滿足Ck連續(xù)。這是個(gè)問題。
3.Geometric Continuity
實(shí)際工程設(shè)計(jì)中,人們有一種直觀的感覺:兩線段相連接,只要在連接點(diǎn)有相同的切線就認(rèn)為是光滑的。但按照參數(shù)連續(xù)性度量光滑度,還必須有相同的切矢模長(zhǎng)才能認(rèn)為是C1連續(xù)的。由于參數(shù)連續(xù)性不能客觀準(zhǔn)確度量參數(shù)曲線連接的光滑度,因而經(jīng)常用稱之為幾何連續(xù)性(Geometric Continuity)的方法來(lái)度量曲線的光滑程度。下面給出幾何連續(xù)性的定義:
參數(shù)曲線C(u)是k階幾何連續(xù)的充要條件為:在弧長(zhǎng)參數(shù)化下,曲線是Ck的。因?yàn)樵诨¢L(zhǎng)參數(shù)化下,曲線的參數(shù)連續(xù)與幾何連續(xù)是一致的。
關(guān)于弧長(zhǎng)參數(shù)化相關(guān)概念可參考: http://www.shnenglu.com/eryar/archive/2014/08/25/208127.html
合成曲線在拼接點(diǎn)處滿足不同于Cn連續(xù)性的某一組約束條件,稱為具有n階幾何連續(xù)性,簡(jiǎn)記為Gn。事實(shí)上模型的形狀是與描述它所取的參數(shù)無(wú)關(guān)的,作為形狀的內(nèi)在幾何特征的光滑度及作為度量光滑度的幾何連續(xù)性定義應(yīng)該是獨(dú)立于具體的參數(shù)化的。幾何連續(xù)性放寬了對(duì)參數(shù)曲線光滑度的限制條件,為形狀定義和形狀控制提供了更多的自由度,更適合曲線在交互設(shè)計(jì)中使用,有文獻(xiàn)稱其為視覺連續(xù)性。
4.Curve Continuity
下面通過(guò)一個(gè)具體的例子來(lái)說(shuō)明參數(shù)連續(xù)性和幾何連續(xù)性。最后介紹OPEN CASCADE中對(duì)曲線連續(xù)性的定義。
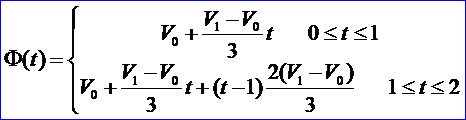
Φ(t)在[0,2]上表示一條連接V0,V1的直線段,但卻有
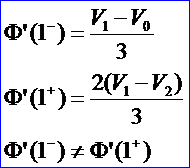
Φ(t)明明是一條直線,卻非C1連續(xù),說(shuō)明用參數(shù)連續(xù)性描述光滑性是不恰當(dāng)?shù)摹?
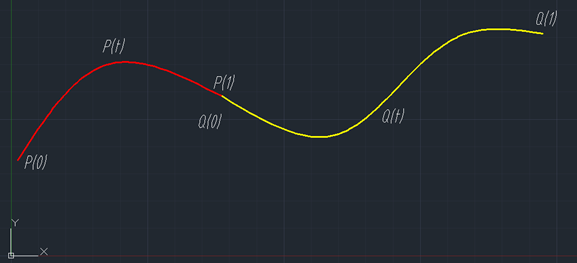
Figure 4.1 兩條曲線拼接的連續(xù)性
如4.1所示,對(duì)于參數(shù)t∈[0,1]的兩條曲線P(t)和Q(t),若要求在拼接處達(dá)到G0連續(xù)或C0連續(xù),即兩曲線在拼接處位置連續(xù),則需要P(1) = Q(0);
若要求在拼接處達(dá)到G1連續(xù),就是說(shuō)兩條曲線在拼接處滿足G0連續(xù)的條件下,并有公共的切矢:
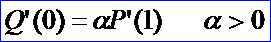
當(dāng)α=1時(shí),G1連續(xù)就成為C1連續(xù)。
若要求在拼接處達(dá)到G2連續(xù),就是說(shuō)兩條曲線在拼接處滿足G1連續(xù)的條件下,并有公共的曲率矢。根據(jù)曲率計(jì)算公式:
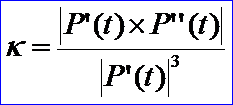
則
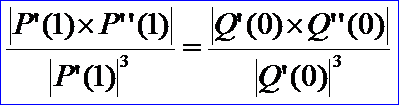
將G1連續(xù)的條件方程代入可得:
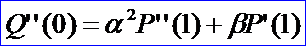
β為任意常數(shù)。當(dāng)α=1,β=0時(shí),G2連續(xù)就成為了C2連續(xù)。至此可以看到,C1連續(xù)保證G1連續(xù),C2連續(xù)保證G2連續(xù),但反過(guò)來(lái)不行。也就是說(shuō)Cn連續(xù)的條件比Gn連續(xù)的條件要苛刻。
OPEN CASCADE中關(guān)于曲線是連續(xù)性的定義使用了GeomAbs_Shape枚舉定義:
//! Provides information about the continuity of a curve:
//! - C0: only geometric continuity.
//! - G1: for each point on the curve, the tangent vectors
//! "on the right" and "on the left" are collinear with the same orientation.
//! - C1: continuity of the first derivative. The "C1" curve is
//! also "G1" but, in addition, the tangent vectors " on the
//! right" and "on the left" are equal.
//! - G2: for each point on the curve, the normalized
//! normal vectors "on the right" and "on the left" are equal.
//! - C2: continuity of the second derivative.
//! - C3: continuity of the third derivative.
//! - CN: continuity of the N-th derivative, whatever is the
//! value given for N (infinite order of continuity).
//! Also provides information about the continuity of a surface:
//! - C0: only geometric continuity.
//! - C1: continuity of the first derivatives; any
//! isoparametric (in U or V) of a surface "C1" is also "C1".
//! - G2: for BSpline curves only; "on the right" and "on the
//! left" of a knot the computation of the "main curvature
//! radii" and the "main directions" (when they exist) gives the same result.
//! - C2: continuity of the second derivative.
//! - C3: continuity of the third derivative.
//! - CN: continuity of any N-th derivative, whatever is the
//! value given for N (infinite order of continuity).
//! We may also say that a surface is "Ci" in u, and "Cj" in v
//! to indicate the continuity of its derivatives up to the order
//! i in the u parametric direction, and j in the v parametric direction.
enum GeomAbs_Shape
{
GeomAbs_C0,
GeomAbs_G1,
GeomAbs_C1,
GeomAbs_G2,
GeomAbs_C2,
GeomAbs_C3,
GeomAbs_CN
};
結(jié)合前面關(guān)于參數(shù)連續(xù)和幾何連續(xù)的介紹,再看頭文件中的注釋就很好理解了。
5.Conclusion
綜上所述,對(duì)拼接曲線光滑度進(jìn)行度量有兩種方法:參數(shù)連續(xù)性和幾何連續(xù)性。參數(shù)連續(xù)性是嚴(yán)格的數(shù)學(xué)可微性定義,就像別人對(duì)你到了年紀(jì)還沒結(jié)婚的看法……“肯定是要求太高了”。而幾何連續(xù)性就像我們工科專業(yè)的,不是那么喜歡較真,差不多就可以了。對(duì)有些精確結(jié)果還喜歡乘以一個(gè)經(jīng)驗(yàn)系數(shù),放點(diǎn)余量。理解了對(duì)拼接曲線光滑性的度量方法,就可以在用到的時(shí)候按需選擇。
6.References
1. 莫蓉. 常智勇. 計(jì)算機(jī)輔助幾何造型技術(shù). 科學(xué)出版社. 2009
2. 王仁宏. 李崇君. 朱春鋼. 計(jì)算幾何教程. 科學(xué)出版社. 2008
3. 孫家廣等. 計(jì)算機(jī)圖形學(xué). 清華大學(xué)出版社. 2000
4. 朱心雄. 自由曲線曲面造型技術(shù). 科學(xué)出版社. 2008
5. Shing Liu. OPENCASCADE Curve Length Calculation. http://www.shnenglu.com/eryar/archive/2014/08/25/208127.html