OPEN CASCADE BSpline Curve Interpolation
eryar@163.com
Abstract. Global curve interpolation to point data is a way to construct curves. The paper focus on the interpolate algorithm in OPEN CASCADE, and give a simple example to demonstrate the usage of the GeomAPI_Interpolate class.
Key Words. Interpolate, NURBS, BSpline, OPEN CASCADE
1.Introduction
曲線曲面擬合Curve and Surface Fitting的方式可以分為兩類：插值interpolation和逼近approximation。采用插值的方式時，所創建的曲線或曲面必須精確地滿足所給的數據條件，例如曲線通過所給的插值點。采用逼近的方式時，創建的曲線或曲面不必精確地滿足所給的數據條件，只要在一定的誤差范圍內接近即可，如下圖所示：
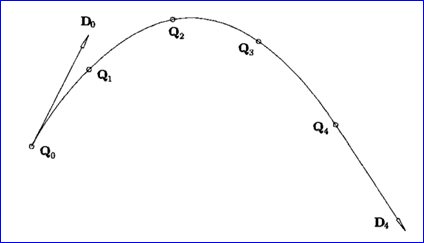
Figure 1.1 A curve interpolating five points and end derivatives(The NURBS Book)
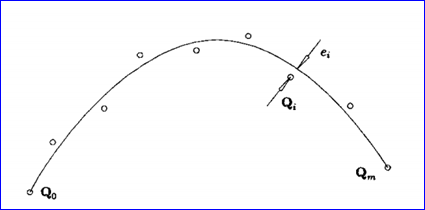
Figure 1.2 A curve approximating points(The NURBS Book)
本文先簡要介紹B樣條插值的原理，再結合OPEN CASCADE源碼說明如何對給定點插值B樣條曲線及OPEN CASCADE中插值曲線的一些注意事項。
2.Global Interpolation
假設給定一組數據點{Qk}，k=0,1,…n，我們想要用一條p次非有理B樣條曲線插值于這些點。如果我們為每個點Qk指定了一個參數值uk，并且選定了一個合適的節點矢量U，我們就可以建立一個系數矩陣為(n+1)x(n+1)的線性方程組：
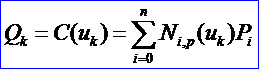
n+1個控制點Pi是未知量。剩下的問題是如何確定Qk對應的參數值uk及節點矢量U，這將影響到曲線的形狀和參數化。常見的選取uk的方法有均勻參數化法、弦長參數化法和向心參數化法。
2.1 Equally Spaced 均勻參數法
假設參數限定在[0，1]范圍內，那么
當參數范圍為[a,b]時，
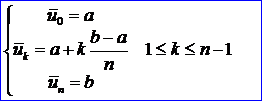
均勻參數化法是最簡單的構造參數的方法，但是不推薦采用這種方法，因為當數據點分布步均勻時，會產生很奇怪的形狀，如打圈自交。
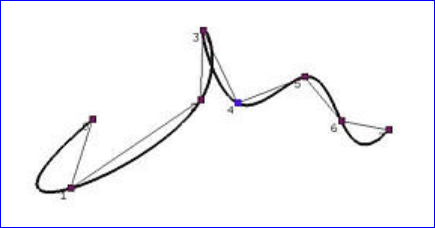
Figure 2.1 B-Spline curve interpolation with the uniformly spaced method[1]
2.2 Chord Length 弦長參數法
令d為總弦長，且把參數范圍限定在[0，1]之間，則：
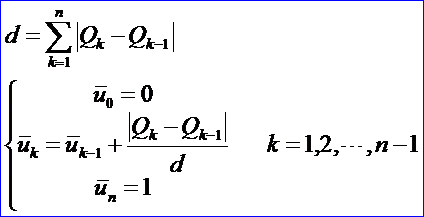
這是最常用的方法，并且一般用它就足夠了，考慮到弦長參數化接近曲線的均勻參數化，在這種意義下，它給出了曲線的一個“好”的參數化。
2.3 Centripetal Method 向心參數法
這是一個更新的方法，當數據點急轉彎變化時，這個方法能得到比弦長參數化更好的結果。
3.BSpline Interpolation in OPEN CASCADE
OPEN CASCADE對曲線的插值是通過GeomAPI包中的GeomAPI_Interpolate實現的。由其代碼注釋可知，這個類的功能是可以對一系列點進行插值得到C2連續的B樣條曲線，當對插值點處的切矢不作要求時。對點直接插值的構造函數為：
GeomAPI_Interpolate (const Handle< TColgp_HArray1OfPnt > &Points, const Standard_Boolean PeriodicFlag, const Standard_Real Tolerance)
其中參數Points為插值點，PeriodicFlag為是否周期曲線，Tolerance是對插值點進行檢查用的容差。Tolerance容易產生誤解，根據插值曲線的定義，插值曲線是要求通過插值點的，所以不存在插值得到的曲線和插值點之間的容差。
經過查看OPEN CASCADE中插值曲線的源碼，可以得出對曲線進行插值的步驟如下：
v 檢查是否有重復的插值點CheckPoints；
v 生成參數BuildParameters；
v 使用BSplCLib::Interpolate()進行插值；
v 根據參數及次數生成系數矩陣，再結合插值點，對系數矩陣和插值點組成的方程組進行求解。
檢查插值點代碼如下：
static Standard_Boolean CheckPoints(const TColgp_Array1OfPnt& PointArray,
const Standard_Real Tolerance)
{
Standard_Integer ii ;
Standard_Real tolerance_squared = Tolerance * Tolerance,
distance_squared ;
Standard_Boolean result = Standard_True ;
for (ii = PointArray.Lower() ; result && ii < PointArray.Upper() ; ii++) {
distance_squared =
PointArray.Value(ii).SquareDistance(PointArray.Value(ii+1)) ;
result = (distance_squared >= tolerance_squared) ;
}
return result ;
}
由上述代碼可知，Tolerance主要是用于檢查插值點是否在容差范圍內有重合現象。生成參數代碼如下：
static void BuildParameters(const Standard_Boolean PeriodicFlag,
const TColgp_Array1OfPnt& PointsArray,
Handle(TColStd_HArray1OfReal)& ParametersPtr)
{
Standard_Integer ii,
index ;
Standard_Real distance ;
Standard_Integer
num_parameters = PointsArray.Length() ;
if (PeriodicFlag) {
num_parameters += 1 ;
}
ParametersPtr =
new TColStd_HArray1OfReal(1,
num_parameters) ;
ParametersPtr->SetValue(1,0.0e0) ;
index = 2 ;
for (ii = PointsArray.Lower() ; ii < PointsArray.Upper() ; ii++) {
distance =
PointsArray.Value(ii).Distance(PointsArray.Value(ii+1)) ;
ParametersPtr->SetValue(index,
ParametersPtr->Value(ii) + distance) ;
index += 1 ;
}
if (PeriodicFlag) {
distance =
PointsArray.Value(PointsArray.Upper()).
Distance(PointsArray.Value(PointsArray.Lower())) ;
ParametersPtr->SetValue(index,
ParametersPtr->Value(ii) + distance) ;
}
}
由上述代碼可知，OPEN CASCADE插值生成參數的方法如下：
不是上述三種常用方法的之一，和弦長參數化法類似，但是沒有去除以總弦長。生成節點矢量之前為了得到曲線的次數，做了如下處理：
if (num_poles == 2 && !myTangentRequest) {
degree = 1 ;
}
else if (num_poles == 3 && !myTangentRequest) {
degree = 2 ;
num_distinct_knots = 2 ;
}
else {
degree = 3 ;
num_poles += 2 ;
if (myTangentRequest)
for (ii = myTangentFlags->Lower() + 1 ;
ii < myTangentFlags->Upper() ; ii++) {
if (myTangentFlags->Value(ii)) {
num_poles += 1 ;
}
}
}
由上述代碼可知，插值要求至少有兩個插值點。當只有兩個插值點時，插值曲線次數為1，即為直線；當有三個插值點且沒有切矢的要求時，插值曲線次數為2次；當插值點數多于3個時，插值曲線次數為3。即對于多于三個點進行插值時，最高只能得到3次曲線，也即C2連續的曲線。進行B樣條插值的代碼如下：
void BSplCLib::Interpolate(const Standard_Integer Degree,
const TColStd_Array1OfReal& FlatKnots,
const TColStd_Array1OfReal& Parameters,
const TColStd_Array1OfInteger& ContactOrderArray,
const Standard_Integer ArrayDimension,
Standard_Real& Poles,
Standard_Integer& InversionProblem)
{
Standard_Integer ErrorCode,
UpperBandWidth,
LowerBandWidth ;
// Standard_Real *PolesArray = &Poles ;
math_Matrix InterpolationMatrix(1, Parameters.Length(),
1, 2 * Degree + 1) ;
ErrorCode =
BSplCLib::BuildBSpMatrix(Parameters,
ContactOrderArray,
FlatKnots,
Degree,
InterpolationMatrix,
UpperBandWidth,
LowerBandWidth) ;
if(ErrorCode)
Standard_OutOfRange::Raise("BSplCLib::Interpolate");
ErrorCode =
BSplCLib::FactorBandedMatrix(InterpolationMatrix,
UpperBandWidth,
LowerBandWidth,
InversionProblem) ;
if(ErrorCode)
Standard_OutOfRange::Raise("BSplCLib::Interpolate");
ErrorCode =
BSplCLib::SolveBandedSystem(InterpolationMatrix,
UpperBandWidth,
LowerBandWidth,
ArrayDimension,
Poles) ;
if(ErrorCode)
Standard_OutOfRange::Raise("BSplCLib::Interpolate");
}
先是根據參數及插值曲線次數生成系數矩陣，再對系數矩陣和插值點構成的方程組進行求解，計算出B樣條曲線的控制頂點Poles。有了節點矢量，次數及控制頂點，B樣條就確定下來了：
myCurve =
new Geom_BSplineCurve(poles,
myParameters->Array1(),
mults,
degree) ;
myIsDone = Standard_True ;
OPEN CASCADE提供的插值接口使用還是很簡單的，如對已經知點進行插值，其用法如下：
int main(int argc, char* argv[])
{
Handle_TColgp_HArray1OfPnt aPoints = new TColgp_HArray1OfPnt aPoints(1, 3);
Handle_Geom_BSplineCurve aBSplineCurve;
aPoints.SetValue(1, gp_Pnt(0.0, 0.0, 0.0));
aPoints.SetValue(2, gp_Pnt(1.0, 1.0, 0.0));
aPoints.SetValue(3, gp_Pnt(2.0, 6.0, 3.0));
GeomAPI_Interpolate aInterpolater(aPoints, Standard_False, Precision::Approximation());
if (aInterpolater.IsDone())
{
aBSplineCurve = aInterpolater.Curve();
GeomTools::Dump(aBSplineCurve, std::cout);
}
}
4.Conclusion
綜上所述，對給定點進行B樣條插值時，需要考慮參數值及節點矢量的選擇。參數值和節點矢量確定后，剩下就是利用B樣條基函數對給定點的參數計算得到的系數組成的線性方程進行求解。
在使用OPEN CASCADE的曲線插值類GeomAPI_Interpolate時，需要注間容差Tolerance是用來對插值點進行檢查的，且插值得到的曲線最高只能是三次曲線。
5.Acknowledgments
首先，感謝cnblog提供了一個表現自己的舞臺http://www.shnenglu.com/eryar/，能在網上和世界連通，知道不是一個人在戰斗。
其次，感謝OPEN CASCADE的開源分享，才得以學到幾何造型相關的知識，比起直接啃國內教材來，學習效率不可同日而語。正如“Talk is cheap, show me the code”所說，將代碼和書本結合起來學習時，收獲更大。
最后，感謝國內外友人對我的肯定和鼓勵，他們自強不息，激情創業的精神總是讓人興奮。
生活的理想就是為了理想的生活The ideal of life is to live for ideals！人生充滿了起起落落，關鍵在于在頂端時盡情享受，在低谷時不失勇氣。
6.References
1. Hongxin Zhang, Jieqing Feng. B-Spline Interpolation and Approximation. Zhejiang University. 2006-12-18. http://www.cad.zju.edu.cn/home/zhx/GM/009/00-bsia.pdf
2. Les Piegl, Wayne Tiller. The NURBS Book. Springer-Verlag. 1995
3. 趙罡, 穆國旺, 王拉柱譯. 非均勻有理B樣條. 清華大學出版社. 1995
4. 易大義, 陳道琦. 數值分析引論. 浙江大學出版社. 1998