OpenCASCADE BRep vs. OpenNURBS BRep
eryar@163.com
Abstract. BRep short for Boundary Representation. First give the definition of the BRep, then compare the BRep mode between OpenCASCADE and OpenNURBS. There are 3 main representation method: use face/edge/vertex to keep track all information in the solid model. The winged-edge data structure uses edges to keep track all information in the solid model. The paper focus on the BRep of OpenCASCADE and OpenNURBS.
Key Words. OpenCASCADE, BRep, OpenNURBS, The Winged-edge Structure,
1. Introduction
計(jì)算機(jī)內(nèi)對(duì)形狀信息的描述方法簡稱為造型(Modeling)技術(shù)���。實(shí)體造型的本質(zhì)是要解決如何在計(jì)算機(jī)內(nèi)部表示一個(gè)實(shí)體模型的問題。以產(chǎn)品實(shí)體造型所建立的三維幾何模型為基礎(chǔ)���,可以進(jìn)一步進(jìn)行運(yùn)動(dòng)力學(xué)分析、模擬裝配��、動(dòng)動(dòng)仿真�����、干涉檢查��、數(shù)控編程以及加工模擬等。造型技術(shù)主要由形狀表達(dá)和形狀操作兩個(gè)部分組成���。形狀表達(dá)的任務(wù)是將形狀的結(jié)構(gòu)用數(shù)據(jù)結(jié)構(gòu)來表示。這種描述形狀的數(shù)據(jù)結(jié)構(gòu)稱為模型(Model)�����。形狀操作的任務(wù)是實(shí)現(xiàn)對(duì)模型的生成���、修改���、綜合�����、分析���、計(jì)算���、顯示等等操作���,以便完成設(shè)計(jì)過程中的各種造型任務(wù)��。造型技術(shù)是CAD的核心技術(shù)之一。目前常用的造型技術(shù)有:實(shí)體造型技術(shù)(Solid Modeling):它將對(duì)象分解為一組有限的三維元素的集合�����,以及可施加在這組集合元素上的一組操作�����、曲面造型技術(shù)(Surface Modeling):它用數(shù)學(xué)函數(shù)如B樣條等來描述曲線曲面�����,并提供曲面的修改,連接�����,求交和顯示等一組操作�����、非幾何形體的造型技術(shù):大多數(shù)自然物體如山水,樹木等。
工程和制造行業(yè)的設(shè)計(jì)對(duì)象主要是三維實(shí)體,因此實(shí)體模型是目前CAD系統(tǒng)的主要造型方法。實(shí)體造型系統(tǒng)的結(jié)構(gòu)如下圖所示:
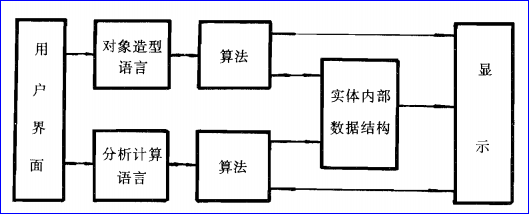
Figure 1.1 Solid Modeling System Structure
實(shí)體在該系統(tǒng)中具有雙層表達(dá):內(nèi)部表達(dá)和在用戶接口中的表達(dá)。在內(nèi)部表達(dá)中��,實(shí)體通常被表達(dá)為頂點(diǎn)��、邊和面的數(shù)據(jù)結(jié)構(gòu)�����,既要滿足各種操作的要求,又要滿足良好的時(shí)空效率的要求�����。在用戶接口中�����,實(shí)體按照可理解性和操作的方便��,使得設(shè)計(jì)人員易于掌握和操作。關(guān)于實(shí)體的操作通常可以分為兩類:一類是關(guān)于形體的操作�����,如生成��、修改��、顯示等;另一類是關(guān)于形體的分析計(jì)算,如計(jì)算實(shí)體的體積���、面積、檢測運(yùn)動(dòng)的實(shí)體間是否接觸等。這些操作各由算法支持,施加于實(shí)體內(nèi)部數(shù)據(jù)結(jié)構(gòu)之上�����。算法往往是組成成模塊�����,分層次實(shí)現(xiàn)。顯示軟件通常要求有三維顯示��、二維投影顯示和真實(shí)感覺顯示等模式��。實(shí)體造型視所用模型的不同�����,通常分為以下三種:
v 結(jié)構(gòu)模型(Constructive Models)
結(jié)構(gòu)模型又稱為構(gòu)造型實(shí)體幾何(Constructive Solid Geometry)�����,簡稱CSG。CSG包含一組簡單的幾何實(shí)體類型,如Box��、Sphere��、Cylinder��、Cone、Torus等。它們稱為基元實(shí)體類型(Primitive Solid Type)���。CSG還包含一組施加于基元實(shí)體類型上的操作,這些操作包含:幾何變換、集合運(yùn)算及剖割等其他造型操作。CSG可以通過這些操作將基元實(shí)體組成復(fù)雜的形狀,滿足設(shè)計(jì)師要求。
v 分解模型 (Decomposition Models)
分解模型的基元實(shí)體只有一種類型,即立方體。和二維圖像由像素(Pixel)組成一樣��,分解模型中的形狀由空間網(wǎng)格中體素的有無而組合構(gòu)成��。體素通常被組織為八叉樹(Octree Representation)的形式�����,以求得更好的時(shí)空效率��。
v 邊界模型 (Boundary Models)
邊界模型采用體��、面、邊���、點(diǎn)的空間坐標(biāo)值和拓樸關(guān)系來表達(dá)實(shí)體模型。邊界模型可以十分精確地描述實(shí)體��,又易與圖形軟件接合��,但是數(shù)據(jù)結(jié)構(gòu)比較復(fù)雜�����。
CSG、分解模型���、邊界模型都是通用模型,它們適用于一個(gè)較大范圍的對(duì)象且達(dá)�����。各種模型各有優(yōu)缺點(diǎn)�����,在實(shí)用中往往要對(duì)各種模型進(jìn)行評(píng)價(jià)�����,然后選擇合適的造型系統(tǒng),評(píng)價(jià)一個(gè)造型系統(tǒng)常常從以下幾個(gè)方面來比較:
v 表達(dá)對(duì)象的能力(Expressive Power)�����;
v 表達(dá)的有效性(Validity)���;
v 模型的緊湊性(Conciseness):即占內(nèi)存空間的大?�。?
v 操作的閉包(Closure of Operations)�����;
v 操作的簡易性(Ease of Operations)�����;
2.Boundary Representation
邊界模型也稱為邊界表示法(Boundary Representation)���,使用實(shí)體的表面來表示實(shí)體的形狀�����。不管實(shí)體的表面形狀是多面體還是自由曲面�����,邊界模型通常都統(tǒng)一為多面體。即用一組三維多邊形所圍成的形體表示實(shí)體��。這種表達(dá)方法是圖形學(xué)基元表達(dá)的一種推廣��,因此邊界表示法與圖形學(xué)有很好的銜接關(guān)系���。組成邊界模型的元素是面Face�����、邊Edge�����、頂點(diǎn)Vertex���。
面可以包括平面���、二次曲面和參數(shù)曲面等��,面中可以有孔,但是面上的無孔部分必須是連通的。一個(gè)無孔的面只帶有一個(gè)邊界���。一個(gè)有孔的面帶有一個(gè)以上的邊界。如下圖所示:

Figure 2.1 Face and its loops
形體由面構(gòu)成,而面是由邊來定義的��,邊則由點(diǎn)來定義�����,點(diǎn)通過三個(gè)坐標(biāo)值來定義�����。如下圖所示為邊界表示的數(shù)據(jù)組織方式:
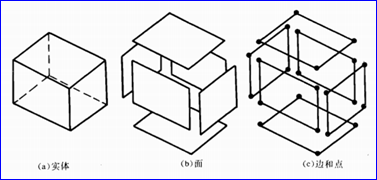
Figure 2.2 Solid, Face, Edge and Vertex of the Brep Model
邊界模型的關(guān)系型數(shù)據(jù)結(jié)構(gòu)可以按照三類方法進(jìn)行組織:以面為基礎(chǔ)的方法,以頂點(diǎn)為基礎(chǔ)的方法及以邊為基礎(chǔ)的方法�����。以面為基礎(chǔ)的方法可以通過面來追蹤實(shí)體的所有信息�����;以頂點(diǎn)為基礎(chǔ)的方法則可以通過點(diǎn)來追蹤實(shí)體的其他信息;以邊為基礎(chǔ)的方法則可以通過邊來追蹤實(shí)體的信息��。
翼邊結(jié)構(gòu)就是以邊為基礎(chǔ)的結(jié)構(gòu)���,通過邊來追蹤實(shí)體的所有信息��。在翼邊結(jié)構(gòu)中��,點(diǎn)、邊��、面之間的拓樸關(guān)系可以通過推理求得��。如下圖所示:
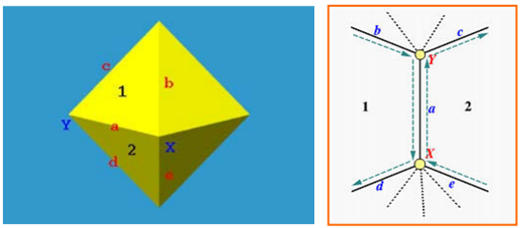
Figure 2.3 The Winged-Edge data structure
邊Edge是整個(gè)數(shù)據(jù)結(jié)構(gòu)的核心���,每個(gè)Edge代表一條邊��,含有九個(gè)域:
1. Edge的編號(hào)ID:a;
2. Edge的起始頂點(diǎn)指針:X�����;
3. Edge的終止頂點(diǎn)指針:Y���;
4. Edge左方向相鄰的面的指針:1;
5. Edge右方向相鄰的面的指針:2;
6. Edge上方向前鄰邊指針:b��;
7. Edge上方向后鄰邊指針:c�����;
8. Edge下方向前鄰邊指針:d�����;
9. Edge下方向后鄰邊指針:e���;
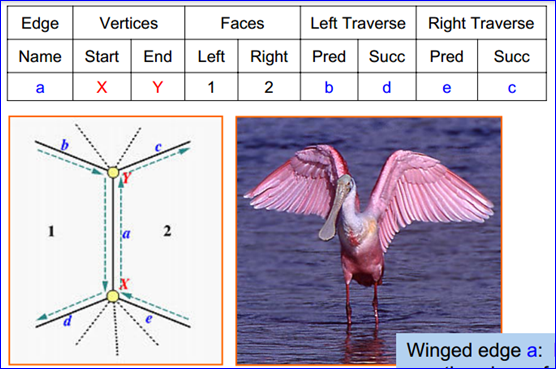
Figure 2.4 The Winged Edge a
由上圖可知��,以邊為基礎(chǔ)的結(jié)構(gòu)很像一只鳥張開的雙翼��,故而得名:The Winged-Edge data Structure。
3.OpenCASCADE BRep
根據(jù)OpenCASCADE中的類的繼承關(guān)系繪制其Brep表示主要的類圖如下所示:
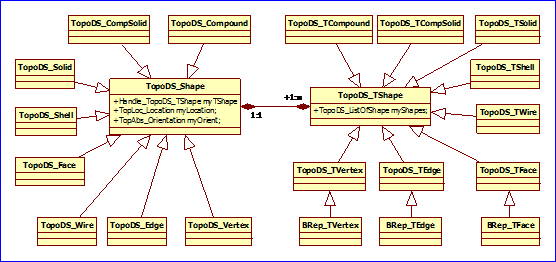
Figure 3.1 OpenCASCADE Brep Class Diagram
由上圖可知��,TopoDS_Shape中有一個(gè)TopoDS_TShape的成員變量���,即TopoDS_Shape包含TopoDS_TShape�����,而一個(gè)TopoDS_TShape中又包含N個(gè)TopoDS_Shape���。這種關(guān)系感覺有些繞���,不過和結(jié)構(gòu)型模式Composite模式有幾分相似���,但不是Composite模式��,因?yàn)門opoDS_Shape與TopoDS_TShape之間只有包含關(guān)系,沒有繼承關(guān)系��,如下圖所示的Composite模式中的Composite類是派生自并且包含Component類的:
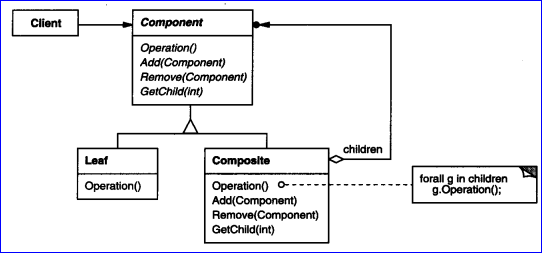
Figure 3.2 Composite Pattern Class Diagram
由圖3.1可知�����,根據(jù)一個(gè)TopoDS_Shape來訪問其子結(jié)構(gòu)很方便���,因?yàn)槠涑蓡T變量myTShape中就包含了其子結(jié)構(gòu)的一個(gè)列表�����。而訪問其父結(jié)構(gòu)是不方便的�����,如要訪問TopoDS_Edge的父節(jié)點(diǎn)數(shù)據(jù)就很不方便���,需要遍歷包含Edge的整個(gè)TopoDS_Shape模型�����。由于這種結(jié)構(gòu)只有包含關(guān)系,所以可以方便地找到父結(jié)構(gòu)到子結(jié)構(gòu)的關(guān)系���,如一個(gè)Face包含哪幾個(gè)Wire或Edge,而沒有直接從子結(jié)構(gòu)找到父結(jié)構(gòu)的拓樸關(guān)系�����,如與一條Edge相關(guān)的所有面是哪些不能直接確定�����。
OpenCASCADE的Brep中幾何信息都是保存在BRep_TFace�����、BRep_TEdge和BRep_TVertex中�����。畫出類圖如下所示:
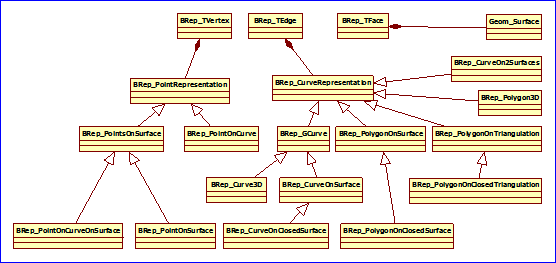
Figure 3.3 Geometry in OpenCASCADE Brep
由上圖可知���,BRep_TVertex, BRep_TEdge, BRep_TFace這三個(gè)類中都包含了幾何信息���,其中頂點(diǎn)和邊包含了幾何信息的一個(gè)列表�����,列表中可以保存多種不同類型的幾何信息���,每種類型都表示了一種幾何之間的關(guān)系��,如頂點(diǎn)的幾何信息中BRep_PointOnSurface就定義了點(diǎn)與面的關(guān)系,邊中的BRep_CurveOnSurface也定義了邊與面的關(guān)系��。即他們的每一個(gè)派生類就描述了一種相互關(guān)系���。OpenCASCADE中的頂點(diǎn)的幾何數(shù)據(jù)包含點(diǎn)��、線和面的幾何之間的一些關(guān)系��,如面上的點(diǎn)、線上的點(diǎn)、PCurve上的點(diǎn)等�����。邊的幾何數(shù)據(jù)包含了線與面的關(guān)系��,如面上的線�����、閉合面上的線、三角網(wǎng)格上的多段線等。而面中包含的幾何數(shù)據(jù)只有面的參數(shù)表示的數(shù)據(jù)�����。
如果硬要往翼邊結(jié)構(gòu)這種方式上來靠���,可以看出OpenCASCADE中從頂點(diǎn)的幾何數(shù)據(jù)出發(fā)�����,可以找到與之有關(guān)的線和面,所以從這方面來說是以頂點(diǎn)為基礎(chǔ)的邊界表示方法�����。而從邊的幾何數(shù)據(jù)出發(fā)只能找到與之相關(guān)的面的信息��,而找不到點(diǎn)的信息��,所以不是翼邊結(jié)構(gòu)。也不是以面為基礎(chǔ)的表示方法�����,因?yàn)槊嬷兄话娴膸缀涡畔?����,沒有與其他幾何數(shù)據(jù)的關(guān)系���。但是OpenCASCADE并不推薦直接訪問TopoDS_TShape的數(shù)據(jù)�����。由類TopoDS_TShape的說明:Users have no direct access to the classes derived from TopoDS_TShape。即這種關(guān)系也不能直接用來訪問���。
4.OpenNURBS BRep
OpenNURBS主要用于NURBS相關(guān)的計(jì)算,代碼清晰簡明��,其中也有關(guān)于Brep的數(shù)據(jù)結(jié)構(gòu)��,結(jié)合其代碼��,將其類圖列出如下所示:
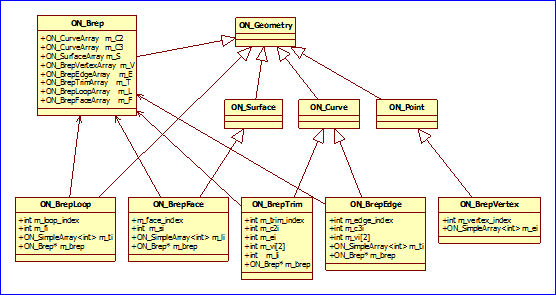
Figure 4.1 OpenNURBS Brep Class Diagram
由上圖可知,類ON_Brep中包含了Brep體的所有幾何及拓樸信息���。幾何信息包含二維參數(shù)曲線m_C2、三維曲線m_C3��、曲面m_S�����;拓樸信息包括頂點(diǎn)m_V��、邊m_E、Trim(m_T)�����、Loop(m_L)���、面m_F���。其它幾種拓樸結(jié)構(gòu)中分別包含信息描述如下:
| ON_BrepFace |
|
| 成員變量 |
變量說明 |
| m_face_index |
Face在ON_Brep中的編號(hào)�����; |
| m_li |
Face中包含的所有Loop的編號(hào)���; |
| m_si |
Face的幾何信息編號(hào); |
| m_brep |
包含所有幾何及拓樸信息的ON_Brep指針; |
| ON_BrepLoop |
|
| 成員變量 |
變量說明 |
| m_loop_index |
Loop在ON_Brep中的編號(hào); |
| m_ti |
Loop中所有Trim的編號(hào)�����; |
| m_fi |
使用這個(gè)Loop的Face的編號(hào)�����; |
| m_brep |
包含所有幾何及拓樸信息的ON_Brep指針���; |
| ON_BrepTrim |
|
| 成員變量 |
變量說明 |
| m_trim_index |
Trim在ON_Brep中編號(hào)��; |
| m_c2i |
Trim的二維參數(shù)曲線; |
| m_ei |
Trim中邊的編號(hào); |
| m_vi[2] |
Trim端部的兩個(gè)頂點(diǎn)編號(hào)��; |
| m_li |
與這個(gè)Trim相關(guān)的所有ON_BrepLoop的編號(hào)���; |
| m_brep |
包含所有幾何及拓樸信息的ON_Brep指針��; |
| ON_BrepEdge |
|
| 成員變量 |
變量說明 |
| m_edge_index |
邊在ON_Brep中的編號(hào)�����; |
| m_v[2] |
邊兩端頂點(diǎn)編號(hào); |
| m_ti |
與這條邊相關(guān)的ON_BrepTrim的編號(hào); |
| m_brep |
包含所有幾何及拓樸信息的ON_Brep指針; |
| ON_BrepVertex |
|
| 成員變量 |
變量說明 |
| m_vertex_index |
頂點(diǎn)在ON_Brep中的編號(hào)�����; |
| m_ei |
從這個(gè)頂點(diǎn)出發(fā)或者回到這個(gè)頂點(diǎn)的邊的編號(hào)�����; |
從上面的類及表格可知��,OpenNURBS的Brep與The Winged-Edge結(jié)構(gòu)很像了,在類ON_BrepTrim中包含了與其他結(jié)構(gòu)之間的關(guān)系���。這個(gè)ON_BrepTrim與ON_BrepEdge的意義類似��。
通過這些編號(hào)及m_brep指針���,可以很容易地訪問到所需要的數(shù)據(jù)�����。也正是通過這些編號(hào)建立起了Brep內(nèi)部數(shù)據(jù)之間的關(guān)系�����,這種方式比較清晰簡單。
5.OpenCASCADE vs. OpenNURBS
綜上所述,可以看出OpenCASCADE中的Brep表示法各有特色�����,下面對(duì)他們的做個(gè)簡單的比較���。
v OpenCASCADE的拓樸結(jié)構(gòu)要多于OpenNURBS���。OpenCASCADE中有TopoDS_Solid, TopooDS_CompSolid, TopoDS_Shell��,而OpenNURBS中沒有這些���。其中OpenNURBS沒有ON_BrepSolid這個(gè)結(jié)構(gòu)��,其實(shí)類ON_Brep已經(jīng)包含了所有幾何及拓樸數(shù)據(jù),相當(dāng)于這個(gè)結(jié)構(gòu)了;
v OpenCASCADE的Brep表示要比OpenNURBS復(fù)雜�����。OpenCASCADE中的TopoDS_Shape和TopoDS_TShape之間的組合關(guān)系及各自類的派生��,使得其Brep表示法不直觀,需要一些面向?qū)ο缶幊痰乃枷氩疟阌诶斫?�。而OpenNURBS中Brep表示要清晰簡單明了�����。幾何之間的關(guān)系(拓樸)通過編號(hào)建立聯(lián)系��,比較直觀。
v OpenCASCADE中的幾何之間的關(guān)系(拓樸)要比OpenNURBS復(fù)雜���。OpenCASCADE中幾何之間的拓樸關(guān)系通過類的成員變量的聚合關(guān)系來表示父結(jié)構(gòu)與子結(jié)構(gòu)之間的關(guān)系。通過類來定義幾何之間的關(guān)系��,如曲線上的點(diǎn)�����,描述了點(diǎn)與邊之間的關(guān)系��,曲面上的線,描述了邊與面之間的關(guān)系等���。正是使用了聚合的關(guān)系,所以從父結(jié)構(gòu)遍歷子結(jié)構(gòu)很方便��,但是不能從子結(jié)構(gòu)直接訪問父結(jié)構(gòu)了���。而OpenNURBS中直接通過編號(hào)來建立這些關(guān)系�����,并且包含ON_Brep的指針���,使得數(shù)據(jù)的查找比較方便,可以直接訪問任何結(jié)構(gòu)��,包括父結(jié)構(gòu)的數(shù)據(jù)���。
v 內(nèi)存使用情況比較���。由于OpenCASCADE中的智能指針Handle的使用��,所以幾何之間的關(guān)系都是使用了這種方式�����,即幾何引用了相同的內(nèi)存數(shù)據(jù)�����。如面上的點(diǎn)和面上的邊這些關(guān)系中,所用的面都是同一個(gè)面的內(nèi)存數(shù)據(jù)���。但是需要內(nèi)存空間來保存描述這些關(guān)系的對(duì)象。OpenNURBS通過編號(hào)來建立這個(gè)拓樸圖�����,只是多了這些編號(hào)的數(shù)據(jù)�����。
v 拓樸數(shù)據(jù)訪問比較��。OpenCASCADE中的拓樸關(guān)系比較復(fù)雜,所以提供了一些訪問函數(shù)���,來便于相關(guān)數(shù)據(jù)的訪問�����。OpenNURBS中可以直接操作這些成員變量��,也可以通過相關(guān)的函數(shù)。在面向?qū)ο蟮某绦蛑校蓡T變量一般可以設(shè)置成private��,以確保數(shù)據(jù)安全��。
v 邊界表示方式比較�����。因?yàn)橐话愕臅隙荚敿?xì)重點(diǎn)描述了邊界表示中以為邊為核心的翼邊數(shù)據(jù)結(jié)構(gòu),所以有人想從這方面來給OpenCASCADE中的Brep表示法來給個(gè)說法。結(jié)合上面的類圖可知,從邊出發(fā)并不能訪問到與這條邊相關(guān)的其他信息,如頂點(diǎn)的信息���。如果硬是想在這里給個(gè)名分,倒是從點(diǎn)出發(fā)可以找到邊及面的幾何信息,所以O(shè)penCASCADE中的Brep表示法應(yīng)該更像是以點(diǎn)為基礎(chǔ)的表示方法��。OpenNURBS中通過ON_BrepTrim�����,可以訪問其他的信息��,而ON_BrepTrim與邊ON_BrepEdge的意義有些相似,所以應(yīng)該是以邊為核心的翼邊結(jié)構(gòu)了�����。
v 幾何數(shù)據(jù)表示的比較�����。OpenCASCADE中幾何數(shù)據(jù)的表示方式很多���,即有常見幾何數(shù)據(jù)的定義,如圓���、拋物線、球面��、圓柱面等��,也有B樣條曲線曲面��。而OpenNURBS統(tǒng)一使用B樣條曲線曲面。有人說分的種類多���,處理有關(guān)算法(如求交算法)時(shí)可分情況來處理,性能較高��。有人說統(tǒng)一使用NURBS曲線曲面來表示�����,算法統(tǒng)一�����,內(nèi)核簡單�����,但是有些算法的性能會(huì)稍差,都沒有完美的解決方案啊。這應(yīng)該留給數(shù)學(xué)家們?nèi)プ非蠛唵巍⒔y(tǒng)一���、高效的方式了。
6.Conclusion
總之,OpenCASCADE與OpenNURBS中的Brep表示法各有特色��。OpenCASCADE使用了更多的類的繼承與組合��,使Brep看起來有點(diǎn)復(fù)雜���。而OpenNURBS中只使用了簡單的繼承,使用編號(hào)來建立拓樸結(jié)構(gòu)�����,看起來要簡單清晰很多��。
從Brep表示法中三種方式:以點(diǎn)為基礎(chǔ)��、以邊為基礎(chǔ)及以面為基礎(chǔ)上來看,OpenCASCADE更像是以點(diǎn)為核心的方式�����,而OpenNURBS更像翼邊結(jié)構(gòu)��。不管以什么方式感覺并不重要�����,只要能方便訪問其拓樸結(jié)構(gòu)即可。不管白貓黑貓��,只看結(jié)果��。
理解Brep表示的數(shù)據(jù)結(jié)構(gòu)后���,可結(jié)合構(gòu)造基本體如立方體�����、圓柱體、球體等的算法��,來理解相關(guān)的造型算法�����,并加深對(duì)Brep表示法的理解。
最后對(duì)OpenCASCADE和OpenNURBS的Brep表示法做的比較都是個(gè)人觀點(diǎn),僅供參考。由于水平所限���,文中的錯(cuò)誤不妥之處在所難免,敬請(qǐng)不吝指教,作者將不勝感激���。
7. References
1. 孫家廣,胡事民. 計(jì)算機(jī)圖形學(xué)基礎(chǔ)教程. 清華大學(xué)出版社. 2009
2. 孫家廣. 計(jì)算機(jī)圖形學(xué). 清華大學(xué)出版社. 2000
3. 莫蓉,常智勇. 計(jì)算機(jī)輔助幾何造型技術(shù). 科學(xué)出版社. 2009
4. Hongxin Zhang, Jieqing Feng. Introduction to Solid Modeling. Zhejiang University.
http://www.cad.zju.edu.cn/home/zhx/GM/015/00-ism.pdf
5. OpenCASCADE: http://www.opencascade.org/
6. OpenNURBS: http://discourse.mcneel.com/category/opennurbs