OpenCASCADE Rational Bezier Curves
eryar@163.com
Abstract. Although polynomials offer many advantages, there exist a number of important curve and surface types which cannot be represented precisely using polynomials, e.g., circles, ellipses, hyperbolas, cylinders, cones, spheres, etc. So we introduce the concepts of rational curves and homogeneous coordinates to solve the problem. To understand rational curves in a homogenous coordinate system is more straightforward. If you define irrational Bezier curves in 4D space and then project them back into 3D space, you obtain rational curves.
Key Words. OpenCASCADE, Rational Curves, Homogenous Coordinate, Geom_BezierCurve
1. Introduction
由于采用了Berstein基函數,Bezier曲線具有許多良好的性質。但是作為多項式曲線,在表示一些“基本”曲線時還是有所不足。例如半徑為1的圓弧曲線,其參數方程可表示為:

圓弧曲線并不是多項式曲線,所以Bezier曲線不可能精確表示像圓弧這樣的簡單曲線。經過參數變換t=tan(u/2),可以把上面的圓弧表示為:
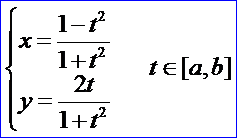
這說明可以用有理多項式來精確表示圓弧曲線。事實上,有很多重要的曲線、曲面類型,如圓、橢圓、雙曲線、圓柱面、圓錐面、球面等,都無法用Bezier來精確表示。由經典數學可知,包括圓在內的所有二次曲線都可以用有理函數(即兩個多項式相除)來表示,即如下形式的有理函數來表示:、
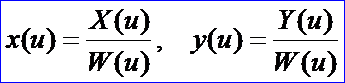
本文主要從齊次坐標的表示法上來理解有理Bezier曲線的概念,及結合OpenCASCADE中的Bezier曲線來理解權因子的幾何意義。
2. Homogeneous Coordinates
在《計算幾何》、《計算機圖形學》或《計算機輔助幾何造型技術》等書中,都會給出有理曲線的齊次坐標(Homogeneous Coordinates)表示法,藉此來從幾何上直觀理解有理曲線的意義。剛開始接觸齊次坐標的概念時,很不能理解,原來這是射影幾何中的一些概念。對此概念陌生的讀者可以參考丘維聲的《解析幾何》,其中對齊次坐標、交比等概念作了詳細解釋。
現在我們來說明齊次坐標與仿射坐標的關系。設點M是平面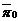 上的通常點,(x,y)是它對于標架[O1:e1,e2]的仿射坐標,則
上的通常點,(x,y)是它對于標架[O1:e1,e2]的仿射坐標,則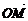 對于標架[O2:e1,e2,e3]的坐標就是(x,y,1),于是點M的齊次坐標(x1,x2,x3)與(x,y,1)成比例:
對于標架[O2:e1,e2,e3]的坐標就是(x,y,1),于是點M的齊次坐標(x1,x2,x3)與(x,y,1)成比例:

其中λ≠0.從而得:
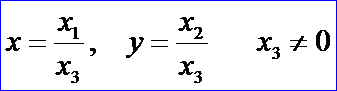
因此,通常點的齊次坐標和仿射坐標可以互相確定。有時我們把通常點M的仿射坐標(x,y)稱為它的非齊次坐標。
從四維Euclidean空間的齊次坐標到三維Euclidean空間的中心投影變換
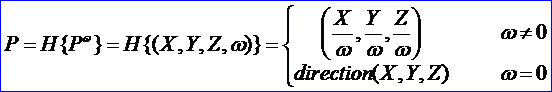
這里三維空間的點[X,Y,Z]稱為四維空間點[X,Y,Z,ω]的透視像,就是四維空間點[X,Y,Z,ω]在ω=1超平面上的中心投影,其投影中心就是四維空間的坐標原點。因此四維空間點[X,Y,Z,ω]與三維空間點[X,Y,Z]被認為是同一點。事實上,對任意X,Y,Z,ω1,ω2,其中ω1≠ω2,有:
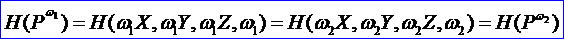
由上可知:一個點的齊次坐標不是唯一的。
在CAGD中描述形狀的空間曲線與曲面都要用到三維空間。但是人類思維能力的限制,我們無法用圖形或模型來表達從四維空間到三維空間的投影變換關系。為了理解這種投影變換的幾何關系,我們可以降低一維,考察從三維到二維空間的投影變換,如下圖所示為三維空間的齊次坐標到二維空間的投影。

Figure 2.1 A representation of Euclidean points to homogeneous form
關于中心投影、射影平面、齊次坐標、變比等概念,可參考丘維聲的《解析幾何》一書。
3. Bezier Curve Perspective Map
在理解射影變換(Perspective Map)及齊次坐標的概念后,可以構造有理Bezier曲線的幾何模型。現假設給定控制點{Pi},權因子{ωi},我們構造帶權控制點:
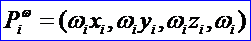
然后在四維空間中定義非有理(即多項式)Bezier曲線:
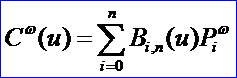
將帶權控制點代入上式詳細寫出每一項得:
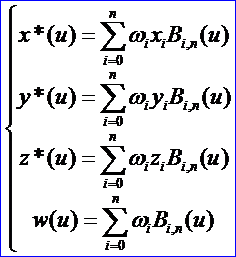
以原點為中心,將四維的Bezier曲線投影到ω=1的三維超平面上,所得到的投影曲線為:
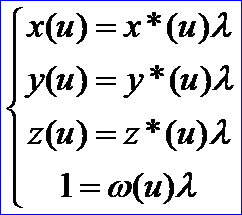
消去λ即得到有理Beizer曲線:
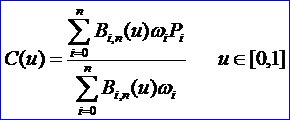
4. The Effects of Weighting Factors
有理Bezier曲線除了具有類似于Bezier曲線的性質外,還增加了關于“權因子”(Weights)的調整性質。
4.1 可退化性
當權因子ωi=ω≠0時(i=0,1,...,n),有理Bezier曲線退化成Bezier曲線。因為ω相同,所以有理Bezier曲線公式中的ω可以消去,又根據Bernstein基函數的規范性即得。使用OpenCASCADE的Tcl腳本測試效果如下圖所示:
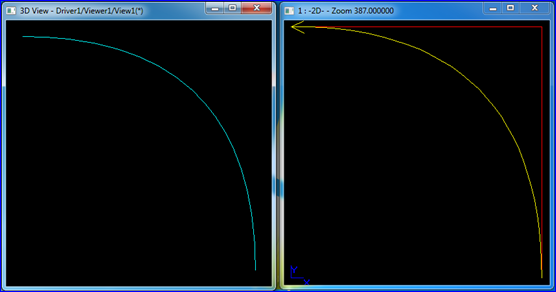
Figure 4.1 Degeneracy of Rational Bezier Curve
相應的Tcl腳本如下所示:
#
# Copyright (c) 2014 eryar All Rights Reserved.
#
# File : degenerate.tcl
# Author : eryar@163.com
# Date : 2014-09-19 18:10
# Version : 1.0v
#
# Description : Demonstrate the degeneracy of Rational Bezier Curve.
#
pload ALL
# Bezier Curve with Weighted Poles:
# {P(1,0), w(1)}, {P(1,1), w(1)}, {P{0,1}, w(1)}
2dbeziercurve bc1 3 1 0 1 1 1 1 0 1 1
v2d
2dfit
# Bezier Curve without weights:
2dbeziercurve bc2 3 1 0 1 1 0 1
mkedge e1 bc2 0 1
vdisplay e1
vtop
vfit
上述Tcl腳本中先把權值相同的有理Bezier曲線顯示在二維窗口中,再將不帶權的Bezier曲線(控制節點與帶權值相同),先生成Edge,再在三維窗口中顯示出來。由圖可知,當有理Bezier曲線的權值相同時,即退化為非有理的Bezier曲線。
4.2 當ω0≠0,ωn≠0時,對任意u∈[0,1],
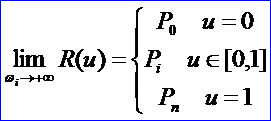
只需證明u∈[0,1]的情況,
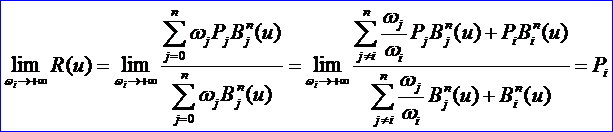
這說明只要ω0≠0,ωn≠0,有理Bezier曲線R(u)一定通過首末控制頂點P0和Pn。對u∈[0,1],當ωi越大,R(u)越趨向于Pi;反之,當ωi越小,R(u)越遠離Pi。
可以看出ωi→∞的極限狀態時,R(u)即過通過Pi。使用OpenCASCADE的Tcl腳本來驗證得到如下圖所示結果:

Figure 4.2 Rational Bezier Curve with different Weights
相應的Tcl腳本如下所示:
#
# Copyright (c) 2014 eryar All Rights Reserved.
#
# File : degenerate.tcl
# Author : eryar@163.com
# Date : 2014-09-19 18:10
# Version : 1.0v
#
# Description : Demonstrate the Rational Bezier Curve with different weights.
#
pload ALL
set w1 0.1
set w2 0.5
set w3 1.0
set w4 2.0
set w5 5.0
set u 0.5
# 4 Bezier Curve with defferent Weighted Poles:
# {P(1,0), w(1)}, {P(1,1), w($w)}, {P{0,1}, w(1)}
2dbeziercurve bc1 3 1 0 1 1 1 $w1 0 1 1
2dbeziercurve bc2 3 1 0 1 1 1 $w2 0 1 1
2dbeziercurve bc3 3 1 0 1 1 1 $w3 0 1 1
2dbeziercurve bc4 3 1 0 1 1 1 $w4 0 1 1
2dbeziercurve bc5 3 1 0 1 1 1 $w5 0 1 1
# mark weight factor.
2dcvalue bc1 $u x1 y1
2dcvalue bc2 $u x2 y2
2dcvalue bc3 $u x3 y3
2dcvalue bc4 $u x4 y4
2dcvalue bc5 $u x5 y5
dtext x1 y1 w1=$w1
dtext x2 y2 w2=$w2
dtext x3 y3 w3=$w3
dtext x4 y4 w4=$w4
dtext x5 y5 w5=$w5
v2d
2dfit
上述代碼顯示了一條三個控制頂點2次的有理Bezier曲線當控制頂點P(1,1)對應的權因子ω變化時的不同的情況。當ω增大時,導致曲線被拉向控制頂點;當ω減小時,導致曲線被推離控制頂點。當ω趨于無窮大時,此時曲線將退化為與控制頂點重合的一個點。
5. Bezier Geometry Curve
OpenCASCADE中的Bezier曲線Geom_BezierCurve本身就是有理Bezier曲線,且都是基于BSplCLib包實現的。即有理Beizer曲線也是NURBS曲線的特例。如下圖所示:
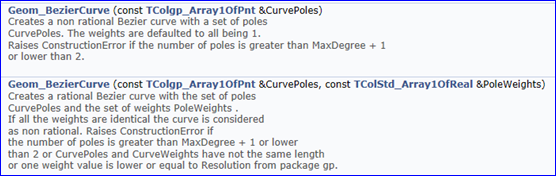
當構造函數只有控制頂點時,將會構造一個非有理的Beizer曲線。當構造函數將控制頂點對應的權因子也設置進來時,將會構造一個有理Bezier曲線。當構造有理Beizer曲線時,若控制頂點的所有權值都相同,則認為是非有理Bezier曲線,即退化性質的體現。
6. Conclusion
綜上所述,由齊次坐標表示法來理解有理Bezier曲線的概念還是比較直觀的,進而可以去理解NURBS曲線曲面的概念。
有理Beizer曲線與非有理Bezier曲線的區別就是權因子。若控制點對應的權因子都相同時,有理Beizer曲線退化為非有理Bezier曲線。且權因子的值越大,則曲線越接近對應的控制頂點。權因子對曲線還有很多重要性質,讀者可以參考其他相關書籍。
OpenCASCADE中的Beizer曲線是基于BSplCLib包實現的,即是NURBS曲線的特例。所以可以表示有理有非有理的Bezier曲線。
7. References
1. 數學手冊編寫組. 數學手冊. 高等教育出版社. 1979
2. 丘維聲. 解析幾何. 北京大學出版社. 1996
3. 蘇步青,劉鼎元. 計算幾何. 上海科學技術出版社. 1981
4. 蘇步青,華宣積. 應用幾何教程. 復旦大學出版社. 2012
5. 莫蓉,常智勇. 計算機輔助幾何造型技術. 科學出版社. 2009
6. 王仁宏,李崇君,朱春鋼. 計算幾何教程. 科學出版社. 2008
7. 趙罡,穆國旺,王拉柱譯. 非均勻有理B樣條. 清華大學出版社. 2010
8. 朱心雄等. 自由曲線曲面造型技術. 科學出版社. 2000
9. 孫家廣. 計算機圖形學. 清華大學出版社. 2000
10. 孫家廣. 計算機輔助幾何造型技術. 清華大學出版社. 2000
11. 王國瑾,汪國昭,鄭建民. 計算機輔助幾何設計. CHEP & Springer-Verlag. 2001
12. Les Piegl, Wayne Tiller. The NURBS Book. Springer-Verlag. 1997
13. Kelly Dempski. Focus on Curves and Surfaces. Premier Press. 2003
14. OpenCASCADE. Test Harness User’s Guide 6.7.1. 2014
15. OpenCASCADE. ModelingData User’s Guide 6.7.1. 2014